Применение к численному методу решения задачи колебаний вала с дисками математического пакета

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №6 2025

УДК 517.85, 534.83                                 

Рассмотренная в работе задача продолжает исследования в вибродиагностике динамических систем по их акустическому отклику [1‒4].

Подобные обратные спектральные задачи невозможно исследовать без решения аналогичных прямых спектральных задач — задач поиска частот свободных колебаний таких систем [5‒7].

Исследования по крутильным колебаниям вала с конечным числом насаженных дисков рассмотрены во многих работах по теории свободных колебаний, в том числе в работах [1, 5‒8].

Поиск частот свободных колебаний многих механических систем (или их частей) с конечным числом степеней свободы часто приводит к образованию дифференциальных уравнений или их систем, решение которых дает вековое уравнение задачи, решаемое затем численным методом. Для задачи крутильных колебаний вала с дисками подобным численным методом является метод Толле, который имеет различные формы [7‒9].

В данной работе приведено использование матричной формы численного метода Толле для для составления частотных уравнений для свободных крутильных колебаний вала с конечным числом дисков, а также дана программная реализация матричного метода с помощью математического пакета Maple на примере вала с пятью дисками

Для использования метода и его матричной формы вал с дисками заменяется на ряд безынерционных участков (Рисунок 1) с упругой податливостью ( , а k , k ₂, ..., k_n__Y — жесткости участков вала), и приведенными массами (дисками) с моментами инерции I , I₂ , ..., I_n .

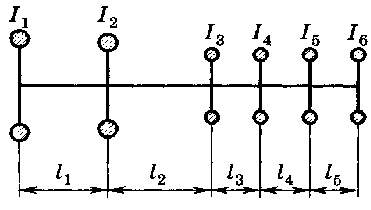
Рисунок 1. Приведенная схема вала с дисками к методу Толле

Метод Толле основан на следующих формулах [1, 8, 9]:

^i = 1;                                         'i

в2 = Q.L- e^2^;

^3 ⁼ ^2 ~ ^e2P²(Jl&L + ^2^2)'

9_n = ^-x - e_n-iP²№+---+^-i9^

в которых — собственная частота крутильных колебаний вала, (          ) — угловые параметры безынерционных участков относительно приведенных масс.

Частотные уравнения методом Толле получены в работе [9] и имеют следующий общий вид для вала с n дисками:

1^0, + izP20z+i3P203+...+i^0n^ ^

Аналитическое решение уравнения (1), выраженного с помощью подстановок рекуррентных формул (1) приводит к проблеме нерациональных расчетов, поэтому к решению подобных задач удобно применить математические пакеты, например пакет Maple, обладающий широкими библиотеками и функциональными возможностями [10‒13].

Приведем программную реализацию матричного метода в пакете Maple на конкретном примере c пошаговыми пояснениями используемых функций и опций пакета.

Рассмотрим вал с 5-ю дисками при известных моментах инерции          масс дисков и погонных жесткостях      участков вала между дисками:

;

X                    Xi                    О                    “                    О

.

Необходимо найти при помощи матричной формы метода Толле соответствующие частоты колебаний вала.

_ 10 Г 1 1

Примем единицу податливости первого участка в виде: ^1   10.48 Le-м I .

Для упрощения расчетов введем безразмерный параметр α , удовлетворяющий условию р² - а- 10⁴ . Тогда вместо Л?² получим также безразмерные произведения /.а ■ lO^i = 1,2,3,4,5.

В итоге с учетом значения e ₁ , имеем равенства:

I_Lp² = 1,03а, 1₂р² = 7,90а, 1₃р² = 1,36а,

14р2 = 2,82а, 13р2 = 2,07а, ех = 1, е2 = 0,30, е3 = 0,43, е4 = 0,26.

Приведем дальнейшую программную реализацию алгоритма в пакете Maple.

• >    restart;

• >    i1p2:=1.03*alpha;    i2p2:=7.90*alpha;    i3p2:=1.36*alpha;    i4p2:=2.82*alpha;

i5p2:=2.07*alpha; e1:=1; e2:=0.30; e3:=0.43; e4:=0.26;

На экране получим числовые данные с присвоенными им соответствующими индикаторами:

i1p2 := 1.03 α i2p2 := 7.90 α i3p2 := 1.36 α i4p2 := 2.82 α i5p2 := 2.07 α e1 := 1 e2 := .30 e3 := .43 e4 := .26

Далее применяем реккурентные формулы (1) матричной формы метода и постепенно получаем на экране выражения значений угловых параметров безынерционных участков через параметр α (при этом также присваиваем им индикаторы):

• >    t1:=1; t1 := 1

• >    t2:=t1-e1*i1p2*t1; t2 ^:= 1 ^- 1^.03 ^α

• >    t3:=t2-e2*i1p2*t1-e2*i2p2*t2; t3 := 1. - 1.3390 α - 2.3700 α (1 - 1.03 α )

• >    t4:=t3-e3*i1p2*t1-e3*i2p2*t2-e3*i3p2*t3;

t4 := 1. - 1.7819 α - 5.7670 α (1 - 1.03 α )

• -    .5848 α (1. - 1.3390 α - 2.3700 α (1 - 1.03 α ))

> t5:=t4-e4*i1p2*t1-e4*i2p2*t2-e4*i3p2*t3-e4*i4p2*t4;

t5 := 1. - 2.0497 α - 7.8210 α (1 - 1.03 α )

• -    .9384 α (1. - 1.3390 α - 2.3700 α (1 - 1.03 α )) - .7332 α (1. - 1.7819 α

• -    5.7670 α (1 - 1.03 α ) - .5848 α (1. - 1.3390 α - 2.3700 α (1 - 1.03 α )))

2.82 α (1. - 1.7819 α - 5.7670 α (1 - 1.03 α )

Полученные значения угловых параметров используем для дальнейшего составления частотного уравнения (2):

> y:=-(i1p2*t1+i2p2*t2+i3p2*t3+i4p2*t4+i5p2*t5);

y := - 1.03 α - 7.90 α (1 - 1.03 α ) - 1.36 α (1. - 1.3390 α - 2.3700 α (1 - 1.03 α )) -

• -    .5848 α (1. - 1.3390 α - 2.3700 α (1 - 1.03 α ))) - 2.07 α (1. - 2.0497 α

• -    7.8210 α (1 - 1.03 α ) - .9384 α (1. - 1.3390 α - 2.3700 α (1 - 1.03 α )) -

  .7332 α (1. - 1.7819 α - 5.7670 α (1 - 1.03 α )

• -    .5848 α (1. - 1.3390 α - 2.3700 α (1 - 1.03 α ))))

Далее при помощи функции «fsolve» находим все решения этого частотного уравнения относительно квадрата частоты в виде:

• >    p2:=10^4*fsolve(y,alpha);

p2 := 0., 3933.804910, 11153.99934, 31515.22971, 50666.64244

Присваиваем индикаторы полученным корням уравнения:

• >    s1:=0; s1 := 0

• >    s2:=3933.804910; s2 := 3933.804910

• >    s3:=11153.99934; s3 := 11153.99934

• >    s4:=31515.22971; s4 := 31515.22971

• >    s5:=50666.64244; s5 := 50666.64244

В итоге остается вычислить соответствующие значения собственных частот как корни квадратные из последних значений:

• >    s11:=sqrt(s1); s11 := 0 > s22:=sqrt(s2); s22 := 62.72005190

• >    s33:=sqrt(s3); s33 := 105.6124961 > s44:=sqrt(s4); s44 := 177.5252932

• >    s55:=sqrt(s5); s55 := 225.0925197

Таким образом, искомые значения частот колебаний следующие:

Pi = 62,6 c-1,p2 = 105,4 c-1,p3 = 175,8 c-1,p4 = 229,1 c-1

(и один нулевой корень, соответствующий общему вращению вала).

Приведенный пример показывает, что при помощи функций пакета Maple можно достаточно быстро реализовать алгоритмы решений многих задач, связанных с прямыми спектральными задачами.

Кроме того, проводить исследования зависимостей частот колебаний от различных параметров рассматриваемых систем (от массовых или жесткостных).