Применение конечно-разностных методов для расчета параметров нефтяного пласта с использованием пакета MathCAD

Одним из практических применений задач высшей математики является их использование при строительстве и эксплуатации скважин нефтедобычи, как добывающего, так и нагнетательного типа. В данном случае возникает необходимость расчета параметров нефтяного пласта (НП), что делает актуальными исследования направлений применения математических методов и программных продуктов в ходе расчетов. Целью исследования является систематизация возможностей оценки распределения давления НП с применением конечно-разностных методов (КРМ) и пакета MathCAD.

Известно, что НП отличается неоднородностью, в связи с различиями в проницаемости как по поверхности, так и в объеме НП. При этом горизонтальные размеры НП существенно выше его толщины h, что позволяет оценивать распределение давления по координатам х и у, с введением понятия гидропроводности £ (способности НП к пропусканию жидкости, насыщающей поры). Параметр £ отличен от единицы при неоднородности НП и связывает толщину НП - h, его проницаемость - к (пропускание при наличии перепада давления) и вязкость жидкости - ц.

Соответственно, вид уравнения для оценки давления НП с горизонтальной неоднородностью будет следующим (1) [1]:

TL (£ £^) + TL (£ £!^) = о; £ = ^ dx V dx/ dy \ dy/            ц

В нашем случае при использовании КРМ, давление, как непрерывная величина, представляется дискретной кусочно-непрерывной функцией, определение которой основано на вычислении значений давления в конкретном числе узлов выделяемых подобластей (конечных элементов).

При анализе двумерной поверхности НП, элементы являются функциями как от х, так и от у. Для решения задачи определяют число, размеры и формы элементов. Выбор узловых точек производится так, чтобы обеспечить лучшее приближение к реальному распределению давления в НП. Далее, использование разностного метода решения краевых задач сводится к аппроксимации исходного уравнения системой разностных уравнений [2]. При этом в явных разностных схемах расчет на следующем шаге основан на уже вычисленных значениях в узлах предыдущего шага, что позволяет организовать «бегущий счет», c применением пакета MathCAD. Графическое представление подобласти с узлами и результата расчетов в MathCAD приведено на рисунке 1.

I i- № -A, j          i+A, j ---O-----□--гтчр-----Q-----0--- i-1-j              i j                   i+1, j i, -A i, j-1^

00054 -0014 n I 10 j) Я CZ —I*----- ' •.uy 1 б а

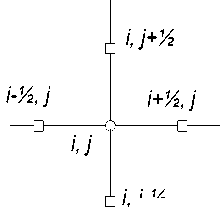
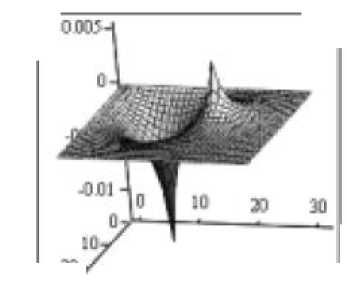
Рисунок 1 – Разностная схема (а) и пример результата в MathCAD [3] (б)

В пакете MathCAD расчет производят на основе разностной схемы (рисунок 1(а)) решения для уравнения (1) краевой задачи Дирихле с использованием пятиточечного шаблона и точности 2го порядка. После замены производных в выражении (1), предполагая линейность решения на каждом звене сетки и используя приближения (2), получаем вторые производные (3); далее вводим массивы ai,j и Рм (4):

dp                    p i+ij -p jj

^Е ах _i+1/2._y ~ ^Е' ^+1/-     Дх

sH^)!

ох \ dx/ I [j

"m'j aU = ~~

^^М-^^)^

Дх2

Приближения (2) вводим для всех промежуточных точек, уравнение (3) и массив (4) получаем как для шага по оси х - Дх, так и по оси у - Ду. Итоговая разностная схема определения давления НП имеет вид (5):

^ai,j^pi+1,j ^{+ a}i-1,j^pi-1,j ⁺ P i,j^pi,j+1 ⁺ P i,j-1 P i,j-1 ^—

⁽ “ i,j + ^ai-1,j ⁺ P i,j ⁺ P i,j-1 ) ^pi,j = ^{0                                  (5)}

и решается вызовом функции multigrid пакета MathCAD. В результате получается матрица (рисунок 1б), точность которой зависит от частоты разбиения области. Недостатками данного подхода при работе в MathCAD остаются сложности кодировок ячеек и узлов, нерегулярность и неравномерность сетки, возможные изменения коэффициентов разностного оператора [4]. Также, для НП возникают сложности учета узлов с особыми свойствами, например, вблизи скважин, с отличными параметрами давления и скачками проницаемости.

Таким образом, рассмотрены возможности применения КРМ и пакета MathCAD для расчета параметров НП. Показан порядок использования разностных схем и способы преобразования уравнений краевой задачи для оценки давления НП с применением MathCAD.