Применение конечно-разностных моделей для краткосрочного прогнозирования природно-ресурсного потенциала Пермского края

Устойчивое экономическое развитие региона напрямую зависит от имеющихся в нем природных ресурсов, от их качества и продуктивности использования. Для повышения эффективности принятия управленческих решений по использованию региональных природных ресурсов, комплексно характеризующихся показателем природно-ресурсного потенциала (ПРП), широко применимы различные методы прогнозирования, основанные на данных открытой статистики. При этом наиболее распространенные методы корреляционного и регрессионного анализа не всегда дают удовлетворительные результаты в экономических исследованиях по причине сложности соответствующих объектов и наличия неявных нелинейных зависимостей между количественными показателями, их характеризующими. В результате коэффициенты полученных таким методом моделей могут оказаться не интерпретируемыми, а сами модели не обеспечивают должно- го качества прогнозирования. В связи с этим возникает необходимость модификации классических методов для получения более приемлемых с прикладной точки зрения результатов при исследовании социально-экономических систем.

1.    Обзор литературы

Обзор актуальных исследований по данной тематике показал их преимущественно экономический характер, кроме того, большинство отечественных работ по данной тематике достаточно старые. Работ, значимых с точки зрения математического моделирования ПРП, в открытом доступе найти не удалось. В частности, ряд авторов разрабатывают вопрос моделирования потоков инвестиций с целью эффективного использования и освоения ПРП на примере различных стран и регионов: Таджикистана [1], Африки [2], Китая [3].Для характеристики ПРП и его элементов широко распространено использование геоинформационно-аналитических систем. В частности, авторы [4] произвели комплексную оценку природного богатства Пермского края, а в [5] рассматривается возможность применения ГИС для управления природными ресурсами различных типов на территории Индии.

ГИС используются и для моделирования отдельных составляющих ПРП. В [6] авторы используют ГИС в комплексе с рядом иных методов для обнаружения и исследования запасов подземных вод в Египте, в [7] ГИС-системы применяются для моделирования и прогнозирования наводнений в Китае.

Достаточно распространено как в отечественных, так и в зарубежных источниках математическое моделирование отдельных элементов природно-ресурсного потенциала. Одним из возможных подходов к оценке эффективности использования ресурсов является построение оптимизационных математических моделей, например в [8] приводятся результаты моделирования добычи природного газа на региональном и мировом уровне. Такой подход предполагает наличие адекватного математического критерия, подлежащего оптимизации, а также системы ограничений, а при их отсутствии данный метод практически неприменим. Исследование [9] посвящено краткому обзору существующих оптимизационных динамических моделей невозобновляемых природных ресурсов. При этом рассматриваются детерминированные модели отдельных ресурсов, что не позволяет напрямую использовать их для случая двух и более их видов, что характерно для большинства регионов. Кроме того, используемый аппарат классической теории оптимального управления требует от исследователя достаточно высокого уровня математической подготовки и может приводить к некорректным результатам применительно к стохастическим экономическим объектам. В работе [10] разработана многокритериальная многофакторная нечеткая модель частично целочисленного программирования для оптимизации распределения сельскохозяйственных водных и земельных ресурсов в условиях неопределенности. Подобное сочетание методов весьма эффективно для решения слабо формализуемых задач, однако требует разработки как специфического математического инструментария, так и программного обеспечения. Это существенно усложняет процесс нахождения решения, растягивает его во времени и требует достаточно высокой квалификации разработчиков соответствующей системы поддержки принятия решения. В целом оптимизационные модели предполагают наличие оптимизируемой функции, т. е. качественного описания объекта в математической форме, в отсутствие такого описания являются неприменимыми.

В работе [11] разработана нелинейная математическая модель управления морскими природными ресурсами в форме системы нелинейных дифференциальных уравнений и выполнено ее исследование в рамках теории устойчивости динамических систем. Применение данного подхода возможно в случае, когда исследуемая система может быть адекватно описана системой обыкновенных дифференциальных уравнений. В [12] авторы применяют детерминированную и стохастическую модели влияния осадков на лесные ресурсы для определения наличия и устойчивости равновесного состояния системы в зависимости от ее параметров и характеристик случайной составляющей. В [13] автором изложена динамическая математическая модель и способ оценки состояния экономики региона с заданным перечнем производств, ресурсов и т. д. в форме системы дифференциальных уравнений. В целом детерминированные факторные модели в большей степени подходят для технических и физических систем, а поведение сложных социальноэкономических систем не всегда адекватно описывают.

Авторы в [14] рассматривают возможность применения балансовых моделей для анализа потребления водных ресурсов. Данный подход не позволяет адекватно характеризовать сложные динамические стохастические объекты, поскольку балансовые модели как правило являются статическими детерминированными.

Еще один распространенный подход к управлению природными ресурсами – моделирование с целью минимизации воздействия на окружающую среду. В [15] предпринята попытка оценки эффективности мероприятий по восстановлению окружающей природной среды в рамках постановки и решения задачи линейного программирования. Авторы в [16] исследуют вопросы моделирования в сфере истощения запасов природных ресурсов и вовлечения ресурсов техногенных месторождений в хозяйственный оборот. В работе [17] авторы изложили способ математического моделирования управления ресурсами и отходами с использованием комплексного подхода.

Достаточно активно в публикациях различных авторов рассматриваются задачи управления процессами отдельных производств, которые эксплуатируют природные ресурсы. Так, в [18] предложены варианты оптимизации управления аграрным сектором, в частности, земельными ресурсами, производством растениеводческой и животноводческой продукции на основании моделей математического программирования со случайными параметрами. В [19] авторами предпринята попытка определения наиболее рационального способа использования энергетических природных и техногенных ресурсов в агротехнологиях на базе эксергетической модели преобразования энергии организмами. В [20] приводится экономико-математическая модель управления производственно-экономической деятельностью сельскохозяйственного предприятия, имеющего специализацию животноводство, являющаяся моделью условной минимизации целевой функции затрат в условиях ограниченных ресурсов. Авторы в [21] анализируют использование водных ресурсов на основе модели экологического следа. Такие исследования, как правило, посвящены конкретным производствам и соответствующим ресурсам, что не позволяет использовать их для управления совокупностью ресурсов в рамках региона.

2.    Материалы и методы

Таким образом, несмотря на многообразие методов, ни один из них не является универсальным. Применимость методов зависит от имеющихся в распоряжении исследователя данных. Это означает, что метод, примененный в одном случае, может оказаться неприменимым в другом. Кроме того, вопрос математического моделирования ПРП на уровне региона вообще и Пермского края в частности разработан недостаточно, а выбор метода есть субъективный выбор исследователя. Соответственно разработка метода, подходящего для целей моделирования и прогнозирования ПРП, позволяющего управлять его уровнем с целью обеспечения устойчивого развития и эффективного использования природных богатств региона, является интересной задачей с теоретической и прикладной точки зрения. Его реализация предполагает:

• 1)    выбор предпочтительного математического метода моделирования; в данной работе рассматривается модификация ЛММ в силу ее простоты, распространенности и использования открытых статистических данных в качестве информационной базы;

• 2)    сбор статистических данных по Пермскому краю, характеризующих составляющие и факторы, определяющие ПРП;

• 3)    построение математического критерия ПРП;

• 4)    моделирование и прогнозирование ПРП Пермского края на основании модифицированной модели множественной линейной регрессии;

• 5)    выработку системы рекомендаций для ЛПР по повышению эффективности краткосрочного управления ПРП.

В рамках данной работы реализуется построение формальной модели природно-ресурсного потенциала (ПРП) на примере Пермского края и обосновываются ее лучшие прогнозные свойства в краткосрочном периоде. С этой целью выделяются факторы, значимые для ПРП Пермского края, производится оценка неизвестных коэффициентов предложенной модели ПРП, осуществляется прогнозирование ПРП на основе классического и разработанного методов, проверка лучших прогностических возможностей предложенного метода.

Под природно-ресурсным потенциалом следует понимать совокупность природных условий и запас природных ресурсов, которые могут быть использованы в хозяйственной деятельности при данном уровне развития техники, технологии и экономических отношений. В частности, под природно-ресурсным потенциалом региона понимается совокупная способность всего многообразия естественных ресурсов и условий территории обеспечивать жизнедеятельность населения и удовлетворять потребности общественного производства на конкретном этапе исторического развития.

Обобщенный критерий ПРП рассчитывается в виде взвешенной суммы отдельных составляющих ПРП [22] Y ( t k ) =a 1 ■ Y ( t k ) + a ₂ ■ Y 2 (t k ) +... + a n ■ Y n ( t k ), где t k - момент времени в пределах изучаемого временного интервала k = 1, 2, . , K . Для определения значений весовых коэффициентов a i , i = 1, 2,..., n частные критерии Y i ( t k ), i = 1, 2, ..., n , k = 1,2,..., K упорядочиваются по степени важности для уровня ПРП (ранжируются), т. е. каждому частному критерию присваивается ранг R i е {1, 2, ... , n }, i = 1, 2, ... , n ; тогда a i = 1 / R i . Поскольку сложные социальноэкономические системы достаточно инертны и, следовательно, меняются медленно, то ранги R_i подбираются таким образом, чтобы обеспечить наиболее плавную динамику сводного показателя ПРП, т. е. минимизируют сумму квадратов разностей его текущего и предшествующего значений:

n ₂

^a i , i = 1,2, ... , n : S = ^ a i ■ ( ^{Y (} t k + 1 ) ^{- Y (} t k ) ) ^ min.                                                 (1)

• i = 1

Дополнительным преимуществом такого метода ранжирования частных критериев является исключение субъективности при упорядочении их человеком. Расчет весовых коэффициентов a i , i = 1, 2, ... , n целесообразно производить по нормированным данным для исключения влияния размерностей частных критериев.

Наличие обобщенного критерия ПРП позволяет сконструировать его линейную множественную регрессионную модель вида m

^ расч ( t k ) = a + С 1 ■ X 1 ( t k ) + c 2 ■ X 2 ( t k ) + ... + C p ■ X p ( t k ) = a + Z c i- X j ( t k ),                          (2)

j '=1

где Y _расч( t_k ) – расчетное значение моделируемой величины в момент времени t k ;

• a – постоянная линейной многофакторной модели, определяющая уровень моделируемой величины при нулевых значениях факторов;

• X _j ( t_k ) – значения факторов, определяющих значение моделируемой величины, в момент времени t_k , j = 1, 2, ... , m ;

c_i – коэффициенты линейной множественной модели, показывающие, на сколько изменится моделируемая величина при увеличении соответствующего фактора X_i на 1.

Управление ПРП осуществляется посредством варьирования определяющих его уровень факторов X j ( t_k ), j = 1,2, ... , m . При этом каждый регион обладает собственными составляющими ПРП Y_i ( t_k ) и набором определяющих их значения (а значит, и уровень собственно ПРП) показателей X _j ( t_k ) . Формальный отбор существенных факторов в уравнение (2) осуществляется на основании анализа матрицы парных коэффициентов корреляции. При этом в модель отбирают такие объясняющие переменные, которые тесно связаны с объясняемой величиной, и слабо – друг с другом [23]. Кроме того, возможно построение модели (2) с помощью пошаговых процедур регрессии, когда факторы добавляются в уравнение или исключаются из него до тех пор, пока происходит увеличение исправленного коэффициента детерминации соответствующих уравнений. Однако, как утверждают многие авторы [24, 25] и показывает практика, формальные процедуры отбора объясняющих переменных не всегда эффективны при моделировании социально-экономических процессов. Это проявляется в неудовлетворительном качестве получаемых уравнений и прогнозов на их основании. В таких случаях приходится выполнять и корреляционный, и качественный анализы и отбирать наиболее значимые факторы с точки зрения природы моделируемого объекта с учетом результатов анализа матрицы парных коэффициентов корреляции.

При изучении динамики показателя естественным является предположение о зависимости его значения в текущий момент времени от значений в предыдущие моменты времени. Для учета такого влияния используются авторегрессионные модели различных порядков, причем порядок модели соответствует максимальному временному лагу. Тогда модификации классической модели множественной линейной регрессии, содержащие авторегрессионные слагаемые первого и второго порядков, примут вид:

m

Y расч ( t k ) = a + b ■ Y ( t k - 1 ) + Z C j ■ X j ( t k ); (3) j = 1

m

Y pac4 ( t k ) = a + b ■ Y ( t k - 1 ) + d ■ Y ( t k - 2 ) + Z C j ■ X j ( t\ (4) j = 1

где b – параметр, показывающий, на сколько изменится моделируемая величина Y ( t_k ) при увеличении значения изучаемой величины в момент времени, предшествующий данному Y ( t_{k –1}), на единицу;

d – параметр, показывающий, на сколько изменится моделируемая величина Y ( t_k ) при увеличении значения изучаемой величины в момент времени t_{k –2} Y ( t_{k –2}) на единицу.

Заметим, что уравнения (3) и (4) могут быть получены путем замены в регрессионнодифференциальных моделях первой и второй производных изучаемого показателя их конечноразностными аналогами [26]. Это дает основание называть уравнения (3) и (4) конечно-разностными моделями первого и второго порядков соответственно.

Проверка качества регрессионных моделей традиционно ограничивается их статистическими характеристиками – значимостью уравнения и его параметров, а также уровнем коэффициента детерминации, характеризующего аппроксимационные свойства соответствующих уравнений. Однако, поскольку добавление в регрессионную модель дополнительных факторов автоматически увеличивает качество аппроксимации, а авторегрессионные слагаемые являются, по сути, добавочными факторами, в нашем исследовании качество регрессионных уравнений оценивается на основании их прогностических свойств. Их оценка для КРМ ПРП выполняется на основании следующего алгоритма:

• –    рассчитывается относительная погрешность прогноза с использованием ЛММ как отношение разности фактического и модельного значений изучаемого показателя к его фактическому уровню, выраженное в процентах;

• –    рассчитывается относительная погрешность прогноза с использованием КРМ как отношение разности фактического и модельного значений изучаемого показателя к его фактическому уровню, выраженное в процентах;

• –    показатель качества прогнозирования с использованием КРМ рассчитывается как частное от деления относительной погрешности прогнозирования КРМ на относительную погрешность прогнозирования ЛММ, умноженное на 100 %.

Таким образом, процедура построения КРМ ПРП Пермского края является итеративной и осуществляется следующим образом:

• 1)    производится анализ матрицы парных коэффициентов корреляции с целью формального исключения тесно взаимосвязанных факторов (устранение мультиколлинеарности);

• 2)    производится качественный анализ оставшихся факторов и проверяется, не исключены ли наиболее значимые с экономической точки зрения факторы из модели и достаточно ли оставшихся факторов для адекватного описания ПРП;

• 3)    оцениваются неизвестные параметры моделей ЛММ (2) и КРМ (3), (4) по укороченным на 1 и 2 значения временным рядам Y(tk) и Xj (t_k), j = 1,2, _, m, k = 1,2, _, K -1(K - 2); при этом знаки коэффициентов при факторах cj-, j = 1,2, .„, m в (3) и (4) совпадают с их знаками в (2) для обеспечения экономической интерпретируемости их значений;

• 4)    рассчитываются прогнозные значения ПРП на основании уравнений (2)–(4) для временных периодов K – 1 и K и сравниваются соответствующие относительные погрешности моделирования ЛММ и КРМ на основании предложенного выше алгоритма;

• 5)    делается вывод о качестве прогнозирования КРМ, если оно неудовлетворительно, возвращаемся к шагу 1, т. е. пересматриваются корреляционный и качественный анализы факторов и модели перестраиваются с новым их набором.

3. Результаты исследования

Для каждого региона составляющие ПРП и факторы, его характеризующие, определяются исходя из его географических особенностей и доступности статистических данных. В случае Пермского края соответствующие показатели представлены в табл. 1.

Таблица 1

Критерии и факторы ПРП Пермского края

Table 1

Natural resource potential criteria and factors for the Perm region

№	Обозначение	Наименование
1	Y 1	Добыча нефти, включая газовый конденсат, тыс. т
2	Y 2	Добыча природного и попутного газов, млн м3
3	Y 3	Производство удобрений минеральных или химических (в пересчете на 100 % питательных веществ), тыс. т
4	Y 4	Продукция сельского хозяйства, млн руб.
5	Y 5	Производство деловой древесины, тыс. плотных м3
6	X 1	Посевные площади сельскохозяйственных культур, тыс. га
7	X 2	Среднегодовая численность занятых в экономике, тыс. чел.
8	X 3	Инвестиции в основной капитал предприятий, млн руб.
9	X 4	Внесение удобрений минеральные удобрения, тыс. т
10	X 5	Внесение удобрений органические удобрения, тыс. т
11	X 6	Стоимость основных фондов на конец года, млн руб.
12	X 7	Лесовосстановление, тыс. га
13	X 8	Число предприятий и организаций на конец года
14	X 9	Цена нефти Brent (среднегодовое значение), USD за баррель
15	X 10	Экспорт продукции ТЭК, млн USD

Необходимые статистические данные по Пермскому краю содержатся в различных источниках федерального и регионального уровней: Федеральная служба государственной статистики, территориальный орган Федеральной службы государственной статистики по Пермскому краю, Лесной план Пермского края на 2018–2027 гг., Стратегия социально-экономического развития Пермского края до 2026 г., государственная программа Пермского края «Воспроизводство и использование природных ресурсов». Для исследования были собраны статистические данные о соответствующих показателях (см. табл. 1) за период с 2001 по 2018 г. На их основании был сформирован комплексный критерий ПРП Пермского края как взвешенная сумма частных критериев в виде Y = Y 1 / 5 + Y 2 / 4 + Y 3 / 2 + Y 4 / 3 + Y ₅ /1.

Отметим, что в связи с внедрением стандарта СНС 2008 (системы национальных счетов 2008) данные в рамках временных рядов оказываются несопоставимым, в связи с чем моделирование производилось на временных интервалах 2001–2008 и 2008–2018. Оценка параметров уравнений (2)–(4) для различных наборов объясняющих факторов и расчет относительных погрешностей прогнозирования выполнены средствами Visual Basic for Applications MS Excel. На основании произведенных расчетов исходя из минимума относительных погрешностей прогнозирования выбирались наиболее качественные модели.

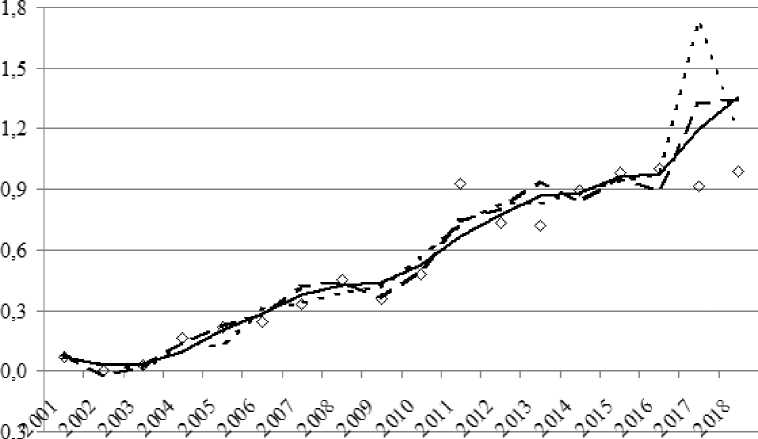
При моделировании ПРП Пермского края не удалось подобрать универсальный набор факторов, адекватно описывающий его динамику на протяжении рассмотренных временных интервалов (табл. 2). Так, при моделировании в период с 2001 по 2018 г. (рис. 1) удалось построить уравнения с приемлемым качеством прогнозирования, включающие факторы Х1, Х3, Х4Х7, Х10. Для периода моделирования 2001–2008 (рис. 2) значимыми оказались факторы Х4, Х5, Х6Х7, Х9, Х10, а для периода моделирования 2008–2018 (рис. 3) – факторы Х1, Х2, Х4, Х6Х7, Х8, Х9, Х10. При этом погрешности прогнозирования с использованием КРМ, как правило, существенно ниже, чем с использованием ЛММ (табл. 3).

При прогнозировании на 1 год вперед обе конечно-разностные модели показали лучшие результаты на всех трех рассмотренных временных отрезках. Лучший результат прогнозирования оказался у КРМ-2 на отрезке 2001–2008 – 3,34 % от уровня погрешности ЛММ. Также весьма неплох КРМ-2 прогноз на отрезке 2001–2018 – 6,46 % от уровня погрешности прогнозирования ЛММ. Несколько хуже результат на отрезке 2008–2018 – 65,55 % от уровня погрешности прогнозирования ЛММ для КРМ-1 и 68,73 % для КРМ-2; тем не менее даже здесь удается улучшить качество прогноза более чем на треть.

Таблица 2

Значения коэффициентов ЛММ, КРМ-1 и КРМ-2 ПРП Пермского края

Table 2 Multiple linear, 1-st and 2-nd type finite difference models coefficients for Perm region

Параметр	ЛММ			КРМ-1			КРМ-2
	2001– 2008	2008– 2018	2001– 2018	2001– 2008	2008– 2018	2001– 2018	2001– 2008	2008– 2018	2001– 2018
a	–1,859	–1,638	0,312	–1,027	–2,679	0,295	–1,202	–3,086	0,313
b	–	–	–	0,032	0,686	0,667	–0,133	0,871	0,580
c 1	–	1,742	–0,429	–	4,594	–0,361	–	5,561	–0,386
c 2	–	–0,576	–	–	–2,894	–	–	–3,678	–
c 3	–	–	0,424	–	–	0,000	–	–	0,000
c 4	0,938	0,173	0,068	0,795	0,000	0,000	0,937	0,000	0,000
c 5	0,311	–	–	0,000	–	–	0,072	–	–
c 6	3,905	1,901	–	1,573	2,095	–	1,634	2,098	–
c 7	0,549	–0,678	0,199	0,525	–1,876	0,064	0,593	–2,318	0,071
c 8	–	1,352	–	–	2,532	–	–	2,998	–
c 9	–1,635	0,926	–	0,000	3,009	–	0,000	3,696	–
c 10	1,125	0,363	0,136	0,660	0,291	0,022	0,763	0,270	0,027
d	–	–	–	–	–	–	0,279	0,129	0,063

О Исходные данные--ЛММ----КРМ-1 - - - - КРМ-2

Рис. 1. Модели ЛММ, КРМ-1 и КРМ-2 ПРП Пермского края в период с 2001 по 2018 г.

Fig. 1. Multiple linear, 1-st and 2-nd type finite difference models for Perm region in 2001–2018

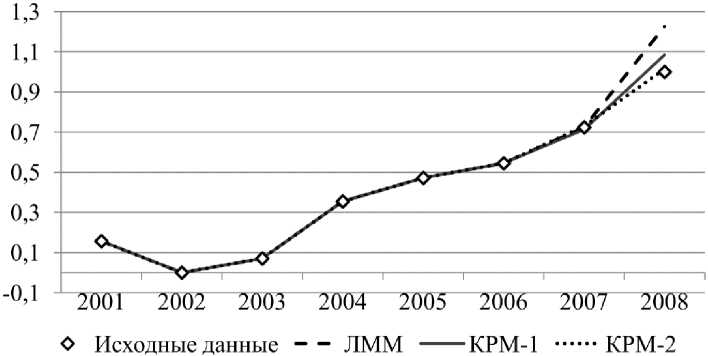
Рис. 2. Модели ЛММ, КРМ-1 и КРМ-2 ПРП Пермского края в период с 2001 по 2008 г.

Fig. 2. Multiple linear, 1-st and 2-nd type finite difference models for Perm region in 2001–2008

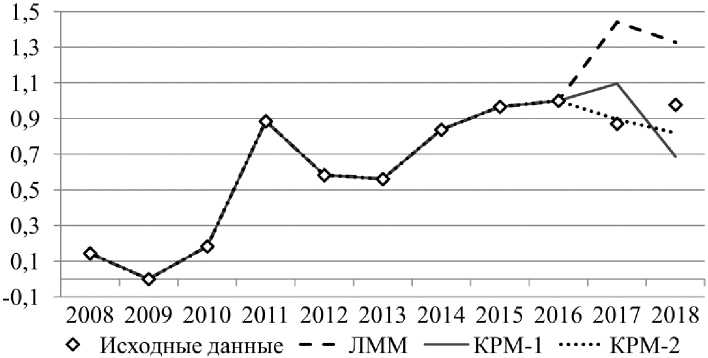
Рис. 3. Модели ЛММ, КРМ-1 и КРМ-2 ПРП Пермского края в период с 2008 по 2018 г.

Fig. 3. Multiple linear, 1-st and 2-nd type finite difference models for Perm region in 2008-2018

Таблица 3

Table 3

Погрешности прогнозирования ПРП Пермского края

Perm region natural resource potential forecasting errors

Временной интервал	Модель	Постпрогноз 1 год	Постпрогноз 2 года
			1 год	2 год
	ЛММ	100	100	100
2001–2008	КРМ-1	35,58	4982,77	37,54
	КРМ-2	3,34	2474,45	6,28
2008–2018	КРМ-1	65,55	–29,77	83,21
	КРМ-2	68,73	–16,29	45,52
2001–2018	КРМ-1	30,30	68,68	103,79
	КРМ-2	6,46	199,05	56,51

При прогнозировании на 2 года вперед целесообразно рассмотреть качество прогнозов на 1 и 2 года. Прогнозы КРМ на 1 год обладают лучшим качеством по сравнению с ЛММ лишь в половине случаев:

– на временном интервале 2008–2018 прогнозы КРМ-1 и КРМ-2 на 1 год существенно лучше ЛММ-прогноза;

– на временном интервале 2001–2018 прогноз КРМ-1 на 1 год более чем на треть лучше ЛММ-прогноза;

– на временном интервале 2001–2008 прогнозы КРМ-1 и КРМ-2 на 1 год намного хуже ЛММ-прогноза;

– на временном интервале 2001–2018 прогноз КРМ-2 на 1 год вдвое хуже ЛММ-прогноза.

Это означает, что использование КРМ, построенных для прогнозирования на 2 года вперед, для прогнозирования на 1 год вперед не всегда нецелесообразно.

Прогнозы КРМ на 2 года обладают лучшим качеством по сравнению с ЛММ в 5 из 6 случаев:

– на временном интервале 2001–2008 прогнозы КРМ-1 и КРМ-2 на 2 года существенно лучше ЛММ-прогноза; при этом прогноз КРМ-2 позволяет добиться погрешности прогнозирования на уровне 6,28 % от погрешности прогнозирования ЛММ;

– на временном интервале 2008–2018 прогнозы КРМ-1 и КРМ-2 на 2 года лучше ЛММ-прогноза; при этом прогноз КРМ-2 позволяет сократить погрешность прогнозирования более чем вдвое по сравнению с погрешностью прогнозирования ЛММ;

– на временном интервале 2001–2018 прогноз КРМ-1 на 2 года несколько хуже (на 3,79 %) ЛММ-прогноза; при этом прогноз КРМ-2 позволяет сократить погрешность прогнозирования более чем вдвое по сравнению с погрешностью прогнозирования ЛММ.

Обсуждение и заключение

Таким образом, краткосрочное прогнозирование ПРП Пермского края с использованием КРМ позволяет добиваться существенно лучшего качества по сравнению с классическими линейными моделями. С учетом логичности добавления авторегрессионных слагаемых в множественную линейную модель, естественности интерпретации коэффициентов при них, а также простоты процедуры оценки параметров КРМ существенно улучшение их прогностических свойств по сравнению с ЛММ. Можно с уверенностью заключить, что их использование для моделирования и прогнозирования ПРП имеет большой научный и прикладной потенциал.