Применение математического пакета Maple к поиску частот колебаний раздаточного редуктора

Бюллетень науки и практики / Bulletin of Science and Practice

Известно, что редукторы, валы, муфты и другие элементы являются важными частями различных технических конструкций, в том числе силовых установок с дизельным топливом, коробок передач и т. д. [1–4].

Рассмотренная в работе задача поиска частот свободных колебаний раздаточного редуктора относится к крутильным колебаниям упруго-массовых систем, опасные динамические или усталостные нагрузки которых могут приводить к различным аварийным повреждениям [5–7]. Такие проблемы чаще решаются с помощью технологий акустической вибродиагностики механических систем или его частей [8–11, 14, 15]. Диагностика же систем как обратная спектральная задача не может исследоваться без моделирований в прямых спектральных задачах [2–5, 12].

В настоящее время существуют возможности применения к исследованиям как прямых, так и обратных задач компьютерных средств, в том числе математических пакетов, программных алгоритмов. В нашем исследовании получена математическая модель к решению задачи определения частот крутильных колебаний раздаточного редуктора как трехмассовой динамической системы и к поиску частот применен функционал математического пакета Maple [13].

Рассмотрим раздаточный редуктор, состоящий из вала с насаженными краевыми подшипниками и передаточной зубчатой шестерней (Рисунок а) как систему с тремя степенями свободы — вала с тремя массами (Рисунок б).

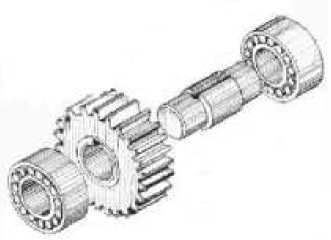
а)

Рисунок. Динамическая модель раздаточного редуктора

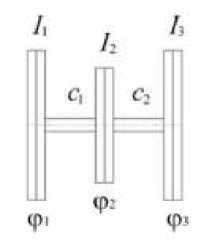
б)

Здесь: ^k ⁽ k 1’3) — обобщенные координаты — углы закручивания масс (подшипников и шестерни); I^{k ( k} = ^1;3) — моменты инерции масс; c ¹ , c ² — коэффициенты жесткостей, с которыми закручиваются участки вала между массами. Такой переход к динамической модели с тремя степенями свободы приводит к известной системе дифференциальных уравнений колебательного процесса в виде [1]:

i I 2

d2^

+ сМ - ^ 2 ) - с 2 ( ^ 2 - %) = °’

I 3

d2^

+ с^ ( ^ - ^ ) = °.

С учетом малых свободных колебаний модели принимаем решения системы (1) по гармоническому закону в виде:

^ _k = M_k cos( pt + а )                                       ⁽²⁾

, где P — собственная частота, Mk (k =1;3) — амплитуды, pt+ а — фаза колебаний в момент времени t.

d4  _

Стандартная постановка функций ^^k и их производных ^{dt  ( k} = ^1;3) в систему (1)

приводит к системе уравнений:

Цр ² M , - с ( M_l - M₂ ) = 0;

I₂p ² M ₂ + с ( M' - M ₂) - c ₂ ( M ₂ - M ₃) = 0;

I₃p ² M₃ + с ( M₂ - M₃) = 0.

Полученную систему (3) решаем относительно нетривиальных значений амплитуд M

( k = 1;3) колебаний и приходим после преобразований соответствующего определителя третьего порядка к вековому уравнению задачи:

I 1 1 2 1 з р ⁴ - ( C i I з ( 1 1 + 1 ₂) + С ₂ 1 1 ( 1 ₂ + 1 з ) ) р ² + C i C ₂( 1 1 + 1 2 + 1 3 ) = 0.

Численные расчеты с помощью векового уравнения (4) позволяют определять значения частот колебаний раздаточного редуктора по известным значениям моментов инерции масс шестерни и подшипников, а также известных коэффициентах жесткостей участков вала редуктора на кручение. Проведенные расчеты важны для установления влияния характеристик механической системы на значения частот и амплитуд ее свободных крутильных колебаний. С помощью векового уравнения (4) проведены также исследования влияния на частоты крутильных колебаний раздаточного редуктора физических параметров масс (моментов инерции масс — шестерни и подшипников) параметров жесткостей (коэффициентов жесткостей на кручение участков вала между подшипниками и шестерней). К проводимым в исследовании аналитическим и численным шагам были использованы функциональные команды и встроенные библиотеки математического пакета Maple [13].

Приведем листинг программы (с пояснениями шагов алгоритма) для определения частот колебаний раздаточного редуктора. Задаем точность работы (вычислений) в пакете. Подключаем библиотеку по линейной алгебре: restart; with(LinearAlgebra):

Формируем характеристический (частотный) определитель задачи:   M:= Matrix(3,

[[i1*p^2-c1, c1, 0], [c1, i2*p^2-c1-c2, c2], [0, c2, i3*p^2-c2]]);

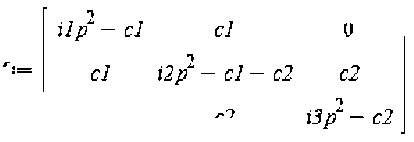
Находим определитель матрицы системы (получаем вековое уравнение):

y:=Determinant(M);

64444 2 2 2

v’= Hi2i3p — clili3p — cli2i3p — с2Ш2р — с2ШЗр + clc2ilp 4- clc2i2p 4- clc2i3p

Группируем уравнение относительно частоты колебаний:   eq:=collect (y, p, distributed);

eq = Hi2i3p 4- (-clШЗ — cli2i3 — c2ili2 — c2ili3)p 4- (clc2il + clc2i2 + clc2i3)p“

Задаем физические параметры системы:   c1:=0.3*10^3; c2:=0.34*10^3; i1:=4.7; i2:=8.2;

i3:=4.3;

cl := 300.0 c2 := 340.00 il := 4.7 i2 := 8.2 В := 4.3

Подставляем значения физических параметров в частотное уравнение:   eq1:=eq;

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №5. 2024

6                   4                      6 2

eql := 165.722/ - 36616.0000/ + 1.754400000 10 /

Решаем вековое уравнение:   p:=fsolve(eq1,p);

p'= -12.27600315, -8.381412884, 0..0., 8.381412884, 12.27600315

Выделяем значения частот колебаний:  p1:=p[5]; p2:=p[6];

pl ■= 8.381412884

p2 ;= 12.27600315

Заметим, что в численной части алгоритма получены частоты колебаний редуктора равные p = 8,3814 с "* и p₂ = 12,2760 с "* при жесткостях c ,= 0,3 - 10 ³ H / м , c ₂ = 0,34 • IO ³ H / м и моментах инерции I = 4,7 кг • м ² , I ₂ = 8,2 кг • м ² , I₃ = 4,3 кг • м ² масс динамической модели.

В заключении отметим, что представление раздаточного редуктора в виде динамической механической модели с тремя степенями свободы (двух краевых подшипников и шестерни, насаженных на валу) позволило найти вековое уравнение свободных крутильных колебаний редуктора стандартными приемами. Разработанные программные решения задачи в математическом пакете Maple подтвердили аналитические выводы, а также рационализировали проведения численных расчетов по полученным моделям задачи.