Применение метаэвристических алгоритмов к решению задач кластеризации методом k-средних

Задача кластеризации – это задача разбиения заданного множества объектов на непересекающиеся подмножества, называемые кластерами, таким образом, чтобы объекты, принадлежащие одному кластеру, были в некотором смысле похожи, а объекты из разных кластеров существенно различались.

Определение . Пусть X – множество объектов, а Y – множество меток кластеров. Тогда алгоритмом кластеризации назовём функцию а : X ^ Y , которая любому объекту из множества X ставит в соответствие метку (номер) кластера из множества Y .

Метод k -средних – один из наиболее популярных методов кластеризации, находящий применение в большом количестве областей, таких как обработка изображений, кластерный анализ, интеллектуальный анализ данных и т. д. [1]. Задача кластеризации методом k -средних может быть сформулирована следующим образом: пусть дано множество точек X = { x 1,..., x n } в метрическом пространстве E n . В соответствии с условиями задачи кластеризации необходимо найти разбиение заданного множества X на к <  n таких подмножеств S = { S 1,..., S_k } , что сумма расстояний точек кластера от их центров минимальна. Фактически необходимо найти

k

min ЕЕ h-ц -I ,                     (1)

i=1 Xj eSi где цi - центр i-го кластера, определяемый по формуле цi =(1|S I)Е xxi . Поскольку по условию En -*            ' Xj e S- j метрическое пространство, ||xj-цi|| = d(xj,цi)>0, где d - расстояние между точками xj- и цi.

Вычислительно задача кластеризации методом k-средних является NP-трудной, а именно: для фиксированных k и размерности пространства d задача решается за время O(ndk+1 log n) [2]. Однако, несмотря на это, существует некоторое количество эвристических алгоритмов, позволяющих быстро находить локальный оптимум для входных данных. Алгоритм Ллойда явля- ется одним из популярных эвристических алгоритмов, применяемых для приближенного решения задач кластеризации. Кратко алгоритм Ллойда может быть описан последовательностью следующих шагов:

• 1.    Случайным образом выбирается начальный набор центров кластеров из к -элементов ц ⁽¹⁾, ^ , ц™ .

• 2.    Для каждой точки x p e X определяется её принадлежность к тому или иному кластеру на шаге t согласно правилу

^xp ^e S⁽ t ), если || ^xp ^— ц ⁽ t )|| <|| ^xp ^- ц /t )|| V j , .

• 1    <  j <  к , i ^ j .

• 3.    Вычисляются новые значения центров кластеров согласно формуле

• 4.    Если положения центров кластеров изменились по сравнению с шагом t -1, переходят к шагу 2. В противном случае работа алгоритма завершается, и возвращаются найденные центры кластеров [3]. Стоит обратить внимание, что алгоритм Ллойда на каждой итерации вычисляет новые положения центров кластеров как центры масс точек, принадлежащих данному кластеру. Отметим, что данная эвристика очень похожа на использованную в работе [4].

ц «+1) =(У ^»)|) Е xe,., xj.

Алгоритм Ллойда имеет следующие недостатки:

• 1.    Не гарантирует достижения глобального минимума функции (1), а лишь одного из локальных минимумов.

• 2.    Результат работы сильно зависит от начального выбора центров кластеров.

• 3.    Число кластеров необходимо знать заранее.

Алгоритм Ллойда используется в качестве базового в большинстве математических и инженерных пакетов ввиду простоты реализации и высокой скорости работы. При этом качество решения задачи кластеризации зачастую оказывается непригодным для дальнейшего анализа, особенно в контексте обработки и анализа изображений, ввиду ограничений, приведённых выше.

Кластеризация в контексте обработки изображений

Важным приложением задачи кластеризации в контексте обработки и анализа изображений является квантование цвета (сегментация изображения). Под квантованием цвета понимается процесс выбора малого числа характерных цветов некоторого изображения. Задачу квантования, таким образом, можно сформулировать как нахождение заданного количества «наилучших» цветов, встречающихся в исходном изображении, и замену всех остальных цветов на наиболее подходящие из найденного множества. При этом кластеризации методом k -средних при помощи алгоритма Ллойда зачастую отдаётся предпочтение ввиду простоты реализации и высокой скорости работы (что особенно актуально в случае обработки потокового видео).

Квантование цвета в том или ином виде зачастую используется как один из этапов процесса анализа изображения. Так, квантование активно используется в моделировании компьютерного зрения, обработке изображений, полученных с телескопов, анализе медицинских снимков и т.д. Резюмируя, можно сказать, что квантование используется в ситуациях, когда необходимо выделить некоторые «области интереса» на изображении или уменьшить количество различных цветов на рисунке.

Отметим, что любое RGB-изображение размера p×q пикселей может быть представлено как матрица Apq, компоненты которой aij являются векторами в пространстве Z3, все элементы r которого ограничены r е [0,255]. Однако в работе с целью повышения наглядности графиков мы будем использовать изображения, у которых третья компонента цвета будет равна нулю, т.е. компонентами матрицы Apq будут векторы в пространстве Z+ (рис. 1). Данное допуще- ние не влияет на результаты, однако позволяет использовать двухмерные графики для представления результатов численных экспериментов.

Рис. 1. Исходное изображение с отфильтрованной синей компонентой в оттенках серого

На рис. 2 показано распределение цветов в исходном изображении.

Зелёиый

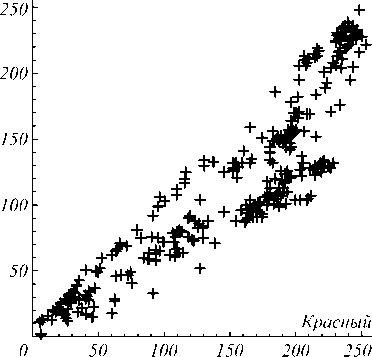
Рис. 2. Распределение цветов в исходном изображении

Кластеризация с помощью метода k-средних как задача непрерывной оптимизации

Рассмотрим задачу (1) в контексте обработки изображений. Как было отмечено, точное решение этой задачи может быть найдено за экспоненциальное время средствами комбинаторной оптимизации. С другой стороны, при некотором фиксированном k задачу (1) можно рассматривать с точки зрения непрерывной оптимизации в пространстве R+k. В этом случае необходимо найти такой вектор Y * е R+k, что f (Y*) < f (Y), V Y е R2+k, где f: R+k ^ R + - целевая функция вида

• 2 к -1        _____________________________________

f ( Y ) = ZE V( X r - y, )² + ( X g - y, +1 ) 2 .           (2)

i =1 x e S .

В функции (2) x_r и x_g – красная и зелёная составляющие цвета некоторой точки изображения соответственно, а Y – вектор, составленный из координат центров кластеров таким образом, что пара ( y ₀, y ₁) является центром первого кластера, ( y ₂, y ₃) – центром второго и т.д. Обобщая: каждый вариант расположения центров k кластеров в пространстве R + содержится в 2 к -мерном векторе Y = { y ₀ , y 1 , y ₂ , у ₃,..., у _{2 к} -1 , у _{2 к} }. Такой вид целевой функции аналогичен использованному в работе [5].

Целевая функция (2) непрерывна, а область её определения компактна [6]. В соответствии с теоремой Вейерштрасса это означает, что предлагаемая целевая функция имеет минимум в области поиска. С другой стороны, способ задания функции не позволяет вычислить её производную, что исключает аналитический подход к поиску глобального минимума, а также не позволяет использовать различные вариации градиентных методов, требующих вычисления производной в конкретных точках. Несмотря на это, глобальный минимум можно постараться найти с помощью численных методов, не требующих манипуляций с производными. К сожалению, многие эффективные алгоритмы оптимизации могут не дать желаемого результата ввиду потенциально большой размерности задачи, а также наличия большого числа локальных минимумов и максимумов целевой функции. Например, широко распространённый метод Нелдера–Мида может «застревать» в локальных экстремумах и не приводить к получению желаемого решения [6]. В этой связи видится разумным использовать для решения задачи алгоритмы, способные «выбираться» из локальных экстремумов. В данной работе для поиска глобального минимума предлагается использовать хорошо зарекомендовавший себя [7] алгоритм гравитационного поиска.

Метаэвристики и алгоритм гравитационного поиска

Метаэвристические алгоритмы (МА) – широкий класс алгоритмов оптимизации, включающий в себя алгоритмы имитации отжига, поиска с запретом, алгоритм роя частиц, генетические алгоритмы и т.д.

Несмотря на то, что внешне МА могут сильно отличаться друг от друга, все они могут быть описаны одной обобщённой формулой. На каждом шаге алгоритм вычисляет очередное решение x^{t+ 1} согласно следующему правилу:

xt+1 = A (xt, p (t)), где A – некоторое отображение, xt – решение на шаге t, а p(t) – параметры, зависящие от конкретного алгоритма, которые также могут зависеть от номера шага t. Также в параметры p(t) в том или ином виде может входить информация о решениях, полученных на шагах [1, t–1].

Предложенный в [8] алгоритм гравитационного поиска (АГП) – относительно новый метаэвристиче-ский алгоритм глобальной оптимизации, основанный на физической модели взаимодействия тел большой массы. Данный алгоритм также можно отнести к классу роевых, т.к. АГП, как и хорошо известный алгоритм роя частиц, основан на развитии многоагентной системы. При этом каждый агент в АГП имеет массу и скорость, а взаимодействие между агентами происходит по правилам классической ньютоновской механики. Таким образом, имеется система из N агентов. Положение i -го агента в пространстве поиска определяется как

• X, = ( x\, _ ,x d , _ ,х П ), i = 1,2, _ , N ,

где x_i^d – координата i -го агента в d -м измерении, а n – размерность пространства поиска.

На шаге t алгоритма сила, действующая на агент i со стороны агента j в d -м направлении, определяется согласно правилу

M ( t ) M ( t )

Fj = G(t) j'' (X(t)-Xd(t)), (3) Ry + e где Mi и Mj – массы i-го и j-го агентов на шаге t, ε – некоторая малая константа, а Rij – Евклидово расстояние между агентами. Обратим внимание, что согласно предложению авторов АГП, основанному на экспериментальных результатах, в формуле (3) фигурирует не квадрат расстояния между агентами, как в формуле классической механики, а обычное Евклидово расстояние.

Результирующая сила, действующая на агент i в d -м направлении, определяется по формуле

N

F ( t ) = £ ra j ( t ),                  (4)

• y =1, j * i

где rand i – случайное число на отрезке [0, 1]. Этот множитель служит для придания стохастических характеристик алгоритму.

В соответствии со вторым законом Ньютона, ускорение i-го агента на шаге t в направлении d определяется как ad (t) = Fd (t)/M, (t),                                 (5)

где M i – масса i -го агента.

Скорость агента на t +1 шаге определяется в соответствии с уравнением движения д X , / д t = — ( д v / д X , ), решение которого даёт следующую итерационную формулу для вычисления нового положение агента относительно шага t [9]:

v^d ( t + 1) = rand . • v^d ( t ) + a , ( t ),                         (6)

x d ( t + 1) = x d ( t ) + v d ( t + 1),                       (7)

где rand_i – случайное число на отрезке [0, 1].

Гравитационная постоянная G инициализируется в начале работы алгоритма и монотонно убывает с течением времени. G может быть задана формулой

t

—a

G (t) = G0 e tmax , где G0 - начальное значение, a - некоторая константа, tmax – максимальное число итераций алгоритма.

На каждом шаге алгоритма массы агентов пересчитываются в зависимости от значения целевой функции. При этом целевая функция принимает меньшие значения в точках, соответствующих агентам с большей массой. Пересчёт значений масс агентов осуществляется по правилу: сначала вычисляются промежуточные значения масс агентов по формуле

M₁ ( t ) = worst ⁽ t )^{— f,t}, ⁽ t ) , worst ( t ) — best ( t )

best (t) = minyE1 N,/ztj( t), worst(t) = maxye1, ,Nfity (t), где fiti(t) равно значению целевой функции в Xi, а worst(t) и besti(t) – худшее и лучшее значения на шаге t соответственно. После чего непосредственно вычисляются массы агентов для данного шага алгоритма

M , ( t ) = MI , ( t )/ ^Mlt t ).

• / j =1

Таким образом, АГП может быть описан в общем виде как следующая последовательность шагов:

• 1.    Определяется пространство поиска (в случае с квантованием цвета пространство поиска R + k , где

• 2.    Случайным образом инициализируется начальное положение N агентов.

• 3.    Рассчитывается значение целевой функции fit j для каждого агента.

• 4.    Вычисляются новые значения G ( t ), best ( t) , worst ( t ) и массы агентов M i ( t ) для i =1,…, N согласно приведённым выше формулам.

• 5.    Рассчитывается значение действующих на агент сил по формулам (3) и (4).

• 6.    Вычисляются новые значения ускорений и скоростей для каждого агента по формулам (5) и (6).

• 7.    Вычисляются новые координаты агентов по формуле (7).

• 8.    Шаги 2–7 повторяются, пока не будет достигнуто условие останова, которым может служить достижение максимального заданного заранее количества итераций.

• 9.    В качестве результата возвращается лучшее найденное положение агента за всё время работы алгоритма.

V r e R² ₊ ^k , r e [0,255]).

Квантование цветов с помощью АГП

Вернёмся к задаче квантования цветов. Формула (2) определяет функцию, которая может быть использована в качестве целевой функции для АГП. Тогда последовательность шагов для решения задачи квантования цвета методом k -средних можно записать следующим образом:

• 1.    Случайным образом сгенерировать N векторов Y , где Y_i = { y_i ⁽¹⁾, y_i ⁽²⁾, … , y_i ^{( k )}, … , y_i ^{(2 k )}} . Таким образом, каждый вектор Y i содержит в себе один из вариантов расположения центров всех k -кластеров. Также определяется максимальное количество итераций t max и устанавливается t = 1.

• 2.    Для каждого агента Y i рассчитывается значение функции (2).

• 3.    Вычисляются новые значения G ( t ), best ( t ), worst ( t ) и массы агентов M_i ( t ) для i = 1,…, N .

• 4.    Рассчитывается значение действующих на агент сил.

• 5.    Вычисляются новые значения ускорений и скоростей для каждого агента.

• 6.    Вычисляются новые координаты агентов. Счётчик t увеличивается на единицу.

• 7.    Шаги 2–6 повторяются, пока t ≤ t_max .

• 8.    Возвращается лучшее найденное положение агента за всё время работы алгоритма.

Результаты численного эксперимента

В качестве исходного изображения для численного эксперимента использовалось стандартное изображение «Лена» с отфильтрованной синей компонентой цвета.

На рис. 3 представлен результат работы алгоритма Ллойда для k = 10. На рис. 4 представлены соответствующие полученному решению кластеры и их центры.

Для эксперимента на основании нескольких пробных запусков были выбраны следующие параметры:

количество агентов N = 30, начальное значение гравитационной постоянной G = 100, количество итераций t max =250.

Рис. 3. Результат работы алгоритма Ллойда, k = 10

Зелёный

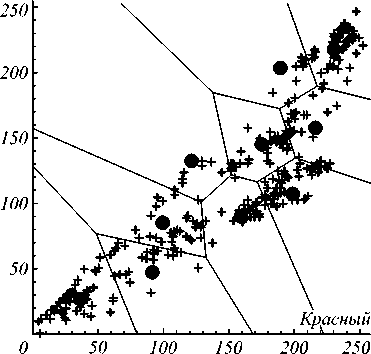
Рис. 4. Кластеры, полученные с помощью алгоритма Ллойда, k = 10

Начальное положение кластеров в соответствии с описанием алгоритма выбиралось случайно в диапазоне от 0 до 255. Также в коде алгоритма был предусмотрен случай, когда одна из координат некоторого кластера «выпадала» из данного диапазона. В такой ситуации агент, содержащий «выпавший» центр кластера, изымался, а на его место ставился случайно сгенерированный.

В табл. 1 представлены значения целевой функции (2) для результатов, полученных с помощью АГП и алгоритма Ллойда (из стандартной поставки пакета Wolfram Mathematica) для тестового изображении при различных k . Видно, что во всех тестовых запусках АГП показал лучшие результаты, чем стандартный алгоритм.

Результат квантования цвета, полученный с помощью АГП для k = 10, приведён на рис. 5. Можно обратить внимание на меньшую «зернистость» полученного изображения.

На рис. 6 приведены кластеры для k = 10, полученные с помощью АГП.

Отметим также интересную особенность решения для k = 10, полученного с помощью АГП. Как видно из рис. 6, один из кластеров оказался «пустым».

Табл. 1. Результаты численного эксперимента

k	Алг. Ллойда	АГП
5	1,64 х 107	3,01 х 106
10	6,13 x 10 6	1,62 х 106
15	4,05 х 106	1,08 х 106
20	3,12 х 106	9,12 х 105
25	2,55 х 106	7,67 х 105
30	2,09 х 106	7,07 х 105
35	1,65 х 106	5,24 х 105
40	1,46 х 106	5,11 х 10 5
45	1,35 х 106	4,23 х 105
50	1,26 х 106	3,97 х 105

Рис. 5. Результат работы АГП, k = 10

Зелёный

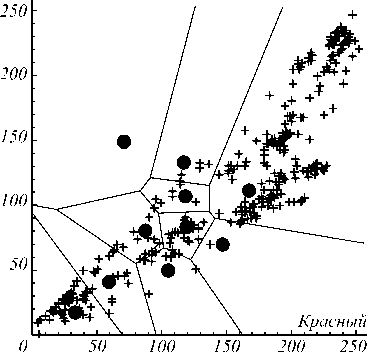
Рис. 6. Кластеры, полученные с помощью АГП, k = 10

Это важное свойство алгоритма, т.к. на первый взгляд может показаться логичным ограничить область поиска центров кластеров выпуклой оболочкой всех точек исходного множества. С точки зрения реализации, это довольно простое изменение [10]. С другой стороны, без подобных ограничений можно увидеть, что алгоритм способен находить решения для общего случая, когда количество кластеров k заранее неизвестно. Это свойство выгодно отличает предложенную схему кластеризации от большинства существующих, требующих жёсткого задания количества кластеров.

Анализ сходимости

Как и для большинства алгоритмов роевого типа, анализ сходимости АГП представляет собой нетриви- альную задачу. В статье [9] приводится сравнительный анализ АГП с алгоритмом роя частиц для поиска глобального экстремума различных унимодальных и мультимодальных тестовых функций. Экспериментальные результаты из [9] говорят о более быстрой сходимости АГП к глобальному оптимуму, чем у алгоритма роя частиц. Несмотря на это, скорость сходимости и точность получаемого решения сильно зависит от выбора начальных параметров. В случае АГП параметры, на которые может влиять пользователь, – это начальное значение гравитационной постоянной G0, число итераций tmax и количество агентов N. Далее обсудим влияние перечисленных параметров на сходимость алгоритма для примера из этой статьи.

Сила, действующая между двумя агентами, пропорционально зависит от G ( t ). Эта сила, в свою очередь, определяет расстояние, на которое может переместиться агент на шаге t . Таким образом, выбирая слишком большое значение G ₀, мы рискуем попасть в ситуацию, когда большая сила, действующая на агент, «выталкивает» его из области поиска решений, что заставляет алгоритм отбрасывать некорректное решение и возвращать агент на случайную позицию в области поиска.

Напротив, слишком малое значение G 0 заставляет агенты двигаться слишком медленно, что приводит к медленной сходимости, даже если направление движения агентов соответствует направлению движения к глобальному минимуму.

Максимальное количество итераций t_max – второй, наряду с G ₀ , параметр, от которого зависит сходимость алгоритма и точность получаемого решения. Большое количество итераций в общем случае означает бо_́ льшую точность получаемых решений. С другой стороны, из-за монотонного убывания G ( t ), начиная с некоторого шага, скорость изменения положения агентов становится крайне низкой. Поскольку при решении задачи квантования цвета нас интересует только целая часть координат агентов, алгоритм может останавливать работу, как только целая часть координат решения стабилизировалась. Помимо этого, параметры G 0 и t max должны быть согласованы таким образом, чтобы за время работы алгоритма G ( t ) достигло достаточно малой величины, но достигло её за достаточно большое число шагов.

Количество агентов N , участвующих в поиске, влияет, прежде всего, на поисковые свойства алгоритма (чем больше агентов, тем выше вероятность попадания хотя бы одного из них в область, где присутствует локальный или глобальный минимум целевой функции). С другой стороны, большое количество агентов сильно замедляет работу алгоритма, т.к. в ходе его работы на каждом шаге вычисляется взаимодействие каждого агента с каждым. Этот факт может быть критичным, учитывая большие объёмы вычислений, проделываемых алгоритмом.

Параметры запуска, использованные в работе, были получены экспериментальным путём. Для этого было произведено несколько пробных запусков с раз- личными параметрами и сравнение получаемых результатов.

Заключение

В статье продемонстрирован подход к решению задач кластеризации методом k -средних путём сведения их к задачам непрерывной оптимизации и применения к ним метаэвристических алгоритмов оптимизации. В качестве примера рассмотрено решение задачи цветового квантования изображения с помощью алгоритма гравитационного поиска. Предложенный метод продемонстрировал высокое качество результатов по сравнению со стандартными средствами цветового квантования математических пакетов (в частности, из состава математического пакета Wolfram Mathematica) при более низкой скорости работы.

Резюмируя, можно сказать, что предложенный подход к квантованию изображений имеет следующие преимущества:

• 1.    Высокое качество получаемых результатов.

• 2.    Способность находить решения даже при неизвестном количестве кластеров.

• 3.    Простота реализации.

Также у предложенного подхода имеются и недостатки:

• 1.    Относительно низкая скорость работы (что может стать серьезной проблемой при обработке потокового видео).

• 2.    Необходимость переформулирования задачи в виде задачи нелинейного программирования.

• 3.    Зависимость размерностей оптимизационной задачи от количества необходимых кластеров.

Также следует отметить, что несмотря на то, что в статье решение задачи кластеризации привязано к задаче обработки изображений, полученные результаты могут быть применены и в общем случае для кластеризации методом k -средних.