Применение метода деревьев классификации к прогнозированию уровня развития моторики у больных с нарушениями двигательных функций

Проблемы управления применительно к медико-биологическим системам связаны с необходимостью принятия решений в условиях многофакторности. Для этого требуется многомерный анализ связей и взаимозависимостей между факторами, которые пока не удается объяснить с позиции физиологических механизмов, действующих в организме человека.

На сегодняшний день развитие средств и методов регистрации и хранения данных позволяет накапливать большие объемы медико-биологической информации.

В частности, в области реабилитации инвалидов собран большой массив данных, характеризующих обследование и лечение больных детским церебральным параличом (ДЦП). Особенность реабилитации больных ДЦП заключается в необходимости применения на практике реабилитационных стратегий, направленных как на восстановление утраченных двигательных функций, так и на развитие новых моторных навыков.

В связи с этим представляется актуальным применение математических методов к анализу медико-биологических данных с целью восстановления взаимозависимостей между факторами, характеризующими состояние больного.

Возможности применения математических методов анализа в различных областях медицины исследуются в работах, посвященных поиску функциональных и логических закономерностей в кардиологии [12, 15], пульмонологии [2, 3, 7], неврологии [9, 11], хирургии [5].

Целью настоящей работы является изучение возможностей применения метода деревьев решений в прогнозировании двигательного развития больных детским церебральным параличом.

Метод деревьев решений

Метод деревьев решений – один из автоматизированных методов многомерного анализа, входящих в технологию Data Mining , отличающийся наглядностью и удобством представления закономерностей [8].

Дерево решений представляет собой древовидный граф – структуру данных, состоящую из узлов принятия решений, соединенных друг с другом ребрами. В дереве имеется один особый узел, именуемый корневым узлом. Другие особые узлы, находящиеся в конце любой цепочки подряд идущих ребер, называют листовыми узлами.

Дерево строится на основании обучающей выборки, содержащей информацию о значениях входных переменных и соответствующих значениях прогнозируемого показателя.

Узел принятия решений обеспечивает проверку условия на значение входной переменной, а каждое ребро обозначает один из возможных вариантов.

Если корневому узлу соответствует всё множество данных, то в результате деления в узле принятия решений это множество разбивается на непересекающиеся подмножества, как показано на рис. 1.

В каждом узле дерево решений выводит значение прогнозируемого показателя в зависимости от значений входных переменных.

По типу прогнозируемого показателя деревья решений подразделяются на два разных вида: деревья классификации и деревья регрессии. Дерево решений с непрерывным прогнозируемым показателем именуется деревом регрессии, деревья классификации, напротив, прогнозируют дискретные показатели.

На сегодняшний день существует несколько различных алгоритмов построения

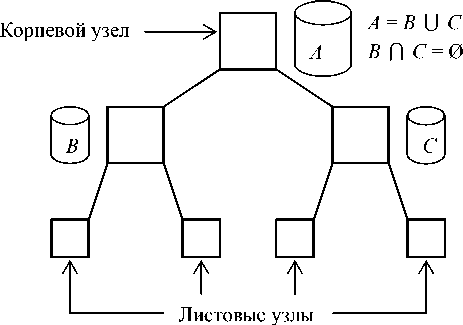
Рис. 1. Структурная схема дерева решений деревьев решений. Наиболее известные: CART – алгоритм построения бинарных деревьев решений (в каждом узле происходит деление не более чем на две ветви), C4.5 – алгоритм построения деревьев с неограниченным количеством ветвей в узлах (строит только деревья с дискретными прогнозируемыми показателями), CHAID – наиболее гибкий алгоритм, позволяющий строить как деревья классификации, так и деревья регрессии с любым количеством ветвлений в узлах [14].

В настоящей работе применялся метод построения деревьев решений CHAID ( Chi square automatic interaction detection ). Метод CHAID основан на проверке гипотезы о независимости двух переменных по критерию х 2 [6].

В соответствии с данным методом для оценки корреляции между двумя категориальными переменными x ₁ и x ₂ (с S - и K -категориями соответственно) строится таблица сопряженности, представляющая собой матрицу N с S строками и K столбцами. Значением элемента n j ( i = 1, S , j = 1, K ) матрицы N является количество случаев одновременного наблюдения i категории признака x ₁ и j категории признака x ₂ .

Далее предполагаем, что переменные являются независимыми в том случае, если вероятность совместного наблюдения i категории признака x ₁ и j категории признака x ₂ равна произведению вероятности наблюдения i категории x ₁ и вероятности наблюдения j категории x ₂ .

P ( i - j ) = P ( i ) - P ( j ).                                        (1)

Переходя от вероятностей к частотам, находим для каждой ячейки таблицы сопряженности ожидаемое в случае независимости переменных количество наблюдений n_ij [10].

KS

E n ik ^- E n sj

~_y = -— s = ^L—,                       (2)

n где n – общее число наблюдений.

На основании реальных и ожидаемых значений n_ij и n ^~ _ij вычисляется статистика критерия x 2 [1].

SK x0 =EE i=1 j=1

^{( n}j - ⁿj )²

nij

Если гипотеза о независимости переменных верна, то значение х 2 имеет распределение х 2 с v = ( S - 1)( K - 1) степенями свободы.

Считается, что связь между переменными существует, если х0 >xmin =Х12-а (v),                                      (4)

где х 2 _-а ( v ) определяется из уравнения

P ⁽ Х 0 ^X ^in ) = ^{1 -а} ,                                 ⁽⁵⁾

где P - вероятность, а - заданный уровень значимости.

На первом шаге алгоритма CHAID оценивается влияние каждой входной переменной на прогнозируемый показатель. Для этого находятся соответствующие парные значения х 2 .

Из всего множества входных переменных, для которых выполняется условие Х о > X min , выбирается та, которой соответствует наибольшее значение Х 2 (переменная, оказывающая наиболее значимое влияние на прогнозируемый показатель).

Значение именно этой переменной проверяется в корневом узле. Каждой категории переменной ставится в соответствие одно из исходящих ребер, заканчивающихся узлом принятия решений. Образованные таким образом узлы соответствуют подмножествам исходного множества. Дальнейшая проверка по критерию Х 2 производится по отдельности для каждого подмножества. Процедура продолжается до тех пор, пока не выполнится некоторое ограничение на рост дерева.

Одним из условий окончания процедуры может являться ограничение на минимальное количество объектов подмножества, соответствующего узлу принятия решений.

В случае когда одна из переменных, участвующих в проверке влияния по критерию Х 2 , является непрерывной, её необходимо категоризовать. С этой целью диапазон изменения значений рассматриваемой переменной делят на некоторое число интервалов, каждому из которых ставят в соответствие одну из категорий. При этом стремятся к тому, чтобы в результате категоризации в каждый интервал попало примерно одинаковое количество наблюдений.

При построении дерева решений стремятся к тому, чтобы на конце каждого из исходящих из узла принятия решений ребер было сосредоточено подмножество с уникальными (не повторяющимися в других подмножествах данного узла) свойствами прогнозируемого показателя.

В связи с этим после категоризации непрерывных переменных решают задачу объединения тех категорий, которым соответствуют подмножества объектов с примерно одинаковыми статистическими характеристиками прогнозируемого показателя.

Иными словами, объединить необходимо те подмножества, в которых значения прогнозируемого показателя встречаются с примерно одинаковыми (близкими) частотами.

Следует отметить, что в случае категорированных непрерывных переменных возможно объединение только соседних категорий.

Аналогичная задача объединения близких с точки зрения прогнозируемого показателя категорий решается и для всех категориальных переменных, принимающих больше двух значений. Однако в данном случае возможна любая комбинация категорий.

Применение метода деревьев классификации К АНАЛИЗУ МЕДИКО - БИОЛОГИЧЕСКИХ ДАННЫХ

Для иллюстрации возможностей выявления скрытых иерархических закономерностей применительно к данным медико-биологической природы было исследовано влияние переменных, характеризующих состояние больного детским церебральным параличом (ДЦП), на комплексный показатель моторики больного.

Деревья классификации строились на основании данных, собранных при обследовании и лечении больных в ГКУ СОН «Центр комплексной реабилитации инвалидов». Во время обследования у каждого пациента были зарегистрированы значения 62 параметров, характеризующих комплексное состояние больного ДЦП.

В число параметров входили факторы, описывающие текущее состояние пациента, возраст больного на момент обследования, характеристики состояния пациента к началу заболевания (т.е. к моменту рождения), а также характеристики дородового состояния больного.

В качестве одного из показателей моторики пациента может рассматриваться индекс моторики (ИМ) – величина, характеризующая интегральный уровень развития двигательных способностей больного. ИМ можно считать непрерывной величиной, измеряемой в интервале [0, ИМ_max]. Нижней границе ИМ соответствует наихудшее развитие, верхней – наилучшее. Исходя из методики определения этой величины, на практике в качестве верхней границы ИМ используют, как правило, ИМ max = 60.

В категориальной форме ИМ обычно подразделяют на три категории:

уровень ИМ = 1 - низкий (ИМ е от 0 до 20);

уровень ИМ = 2 - средний (ИМ е от 20 до 40);

уровень ИМ = 3 - высокий (ИМ е от 40 до 60).

Рассмотрим процедуру построения деревьев классификации для прогнозирования уровня ИМ. Построение выполнялось средствами пакета программ SPSS на основании данных обучающей выборки численностью 126 наблюдений.

В соответствии с требованиями алгоритма CHAID был зафиксирован уровень значимости а = 0,05; в качестве критерия остановки алгоритма было установлено минимальное количество случаев в подмножестве N min = 10, кроме того, было задано изначальное (максимальное) число категорий для непрерывных переменных n k = 10.

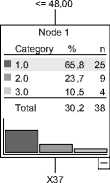
На рис. 2 приведено полученное в результате дерево классификации.

Полученное дерево классификации состоит из узлов принятия решений ( Node ), соединенных ребрами (рис. 2). Для каждого узла дерева указано ограничение на значение входной переменной, а также частотная гистограмма распределения значений прогнозируемого уровня ИМ.

В результате применения метода CHAID было выделено множество значимых входных переменных (табл. 1).

В соответствии с рис. 2 возраст пациента ( X 1) – фактор, оказывающий наиболее сильное влияние на уровень ИМ. Данному фактору соответствует наибольшее значение критерия значимости % ² = 40,68 (см. табл. 1) и, как следствие, значение именно этого фактора проверяется в корневом узле дерева.

Таблица 1

Множество значимых переменных (a)

№ п/п	Значимые переменные	Критерий значимости х 2	Обозначение	Диапазон изменения (обучающая выборка)
1	Возраст пациента (месяцы)	40,68	X 1	(7; 193)
2	Индекс напряжения регуляторных систем (ИНРС) (единицы)	25,23	X 3	(5,53; 1666,67)
3	Низкая масса при рождении	10,25	X 33	да / нет
4	Наличие признаков внутриутробной гипоксии	9,74	X 37	да / нет

Уровень_ИМ

Node 0

n

Total

100,0 126

1.0

2.0

Category %

1.0

2.0

3.0

31,0 39

26,2 33

42,9 54

(48,00, 94,00]

= 33,67

(33,67, 63,66]

(63,66, 133,93]

> 133,93

Рис. 2. Дерево классификации (а)

Четко выделяется тенденция роста уровня ИМ с возрастом. В случае если возраст пациента не превышает 48 месяцев, уровень ИМ в 65,8 % случаев принимает значение «1», что соответствует наихудшему развитию двигательных способностей. Для более старшего возраста ( X 1 > 94 (мес.)) в 66,7 % случаев характерен, наоборот, высокий уровень развития моторики (уровень ИМ = 3).

Описанная тенденция является вполне закономерной. Связана она с тем, что процесс формирования двигательных навыков является многостадийным и иерархическим. Более сложные навыки, как правило, формируются на основе сформированных в раннем возрасте более простых.

Наиболее значимым фактором, оказывающим влияние на уровень ИМ для пациентов в среднем диапазоне возраста X 1 ∈ (48; 94] (мес.), является в соответствии с рис. 2 переменная X 3 – индекс напряжения регуляторных систем (ИНРС). Данный фактор является показателем кардиограммы и характеризует степень напряжения механизмов адаптации человеческого организма. Механизмы адаптации проявляют себя в случае воздействия на организм внешних факторов, например физических нагрузок. При этом в результате медицинских исследований [4] было обнаружено существование двух предельных состояний ИНРС: истощение (низкие значения ИНРС) и перенапряжение (высокие значения ИНРС).

На рис. 2 прослеживается нелинейный характер связи уровня ИМ и ИНРС. Наблюдаемая связь вполне согласуется с зависимостью, полученной в работе [4].

Классифицирующие правила для данного узла будут выглядеть следующим образом:

если X 1 ∈ (48; 94] и X 3<=33,67, то уровень ИМ = 1 с вероятностью 66,7% (истощение);

если X 1 ∈ (48; 94] и X 3 ∈ (33,67; 63,66], то уровень ИМ = 2 с вероятностью 54,5%;

если X 1 ∈ (48; 94] и X 3 ∈ (63,66; 133,93], то уровень ИМ = 3 с вероятностью 81,2%;

если X 1 ∈ (48; 94] и X 3 > 133,93, то уровень ИМ = 3 с вероятностью 50,0%.

Однако в последнем случае также высока вероятность низкого уровня ИМ: если X 1 ∈ (48; 94] и X 3 > 133,93, то уровень ИМ = 1 с вероятностью 40,0% (перенапряжение).

Это говорит о том, что значения индекса напряжения регуляторных систем, превышающие величину «133,93», также могут оказать негативное влияние на развитие двигательных функций больного ДЦП в возрасте от 48 до 94 месяцев.

Полученные математические закономерности отражают неустойчивый характер протекания заболевания ДЦП у пациентов с низким уровнем ИМ. Среди представителей данного класса пациентов встречаются как чрезвычайно высокие значения ИНРС, так и недопустимо низкие.

Необходимо отметить, что к данной обучающей выборке применялся ранее в работе [13] метод пошагового дискриминантного анализа.

В соответствии с алгоритмом метода вся группа пациентов делилась на 3 класса π _i ( i = 1,3 ) в зависимости от уровня ИМ:

π ₁ = { x | уровень ИМ = 1}; π ₂ = { x | уровень ИМ = 2}; π ₃ = { x | уровень ИМ = 3}.

При этом каждому пациенту ставился в соответствие m -мерный вектор параметров x , где m – число параметров, характеризующих состояние пациента.

Задача дискриминации формулировалась следующим образом: требовалось установить критерий, согласно которому по наблюдаемому значению вектора x пациент мог бы быть отнесен к одному из возможных классов πi , характеризующихся различным уровнем ИМ, с вероятностью pi , i = 1,3 .

Интересно подчеркнуть, что в результате пошагового дискриминантного анализа переменная X 3 – индекс напряжения регуляторных систем (ИНРС) – также вошла во множество значимых переменных.

В работе [13] решение о включении переменной во множество значимых факторов принималось на основании проверки F -критерия для всех наблюдений из обучающей выборки.

Метод деревьев решений позволяет получать решающие правила в последовательной иерархической форме. При этом значимость входной переменной оценивается не для всех объектов обучающей выборки, а для каждого из подмножеств, образованных в результате ветвления дерева.

В настоящей работе относительный уровень значимости ИНРС (по F -критерию) для всей выборки оказался значительно ниже, чем для пациентов в возрасте от 48 до 94 месяцев (по критерию χ ² ).

Следует отметить также, что модель деревьев решений наилучшим образом соответствует реальной картине диагностики того или иного заболевания. На практике при попытке диагностировать, например, степень тяжести заболевания врач не требует от пациента собирать сразу все возможные анализы (регистрировать значения всех переменных, характеризующих его состояние). Регистрация входных переменных происходит последовательно, группами. В случае если имеющиеся результаты анализов не дают достаточной уверенности в выбранном значении прогнозируемого показателя, проводится дальнейшее обследование пациента, сопровождаемое регистрацией других переменных [2].

В другом возрастном интервале X 1 <= 48 (мес.) было обнаружено значимое влияние переменной X 37 – наличие признаков внутриутробной гипоксии

(внутриутробного кислородного голодания). Данная переменная характеризует протекание беременности у матери больного ДЦП. На рис. 2 прослеживается негативное влияние данного фактора на развитие моторики больного, особенно ярко выраженное в раннем возрасте пациента.

Еще одним фактором, негативно сказывающимся, наоборот, в более старшем возрасте X 1 > 94 (мес.), является фактор X 33 – низкая масса при рождении.

Таким образом, в результате исследований был также подтвержден тезис о высокой степени влияния на формирование двигательных навыков больного ДЦП факторов, характеризующих состояние больного к моменту рождения, и характеристик дородового состояния больного.

К числу особенностей рассматриваемого метода относится то, что одно дерево классификации не описывает всех существующих зависимостей. Оно отражает только наиболее значимые зависимости. При этом существенное влияние на формирование дерева решений оказывают значения параметров метода, таких как уровень значимости, критерий остановки процедуры роста дерева, изначальное количество категорий для непрерывных переменных.

Для демонстрации данного влияния установим первоначальное количество категорий для непрерывных переменных n_k = 5. Остальные параметры оставим такими же, как и для первого примера. На рис. 3 представлен результат применения алгоритма CHAID пакета программ SPSS с учетом изменений параметров метода.

Небольшие изменения в параметрах модели привели к изменениям границ интервалов возраста, что, в свою очередь, сказалось на дальнейшем выборе наиболее значимых переменных (табл. 2).

Таблица 2

Множество значимых переменных (б)

№ п/п	Значимые переменные	Критерий значимости х 2	Обозначение	Диапазон изменения (обучающая выборка)
1	Возраст пациента (месяцы)	39,50	X 1	(7; 193)
2	Инфицирование	18,61	X 36	да / нет
3	Вес ребенка (граммы)	14,68	X 43	(1222; 4382)
4	Течение предыдущей беременности	10,59	X 12	норма / выкидыш / аборт
5	Наличие признаков внутриутробной гипоксии	6,21	X 37	да / нет

В результате в число значимых переменных вошли новые факторы, и, как следствие, были получены новые классифицирующие правила.

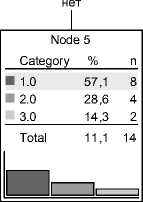
В частности, в возрастном интервале (36; 84] (мес) наиболее значимой по отношению к уровню ИМ оказалась переменная X 36 – инфицирование. Данная переменная характеризует наличие внутриутробного инфицирования плода, вызываемое, как правило, перенесенными в период беременности заболеваниями у матери.

Классифицирующие правила для данного узла принятия решений выглядят следующим образом:

если X 1 ∈ (36; 84] и X 36 = да, то уровень ИМ = 1 с вероятностью 83,3%;

если X 1 ∈ (36; 84] и X 36 = нет, то уровень ИМ = 3 с вероятностью 47,5%.

■ 1.0

■ 2.0

■ 3.0

Уровень_ИМ

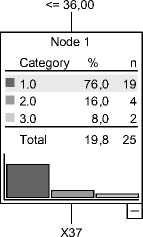
(36,00, 84,00]

Node 2

Category %n

• ■    1.0       32,717

• ■    2.0       26,914

3.0        40,421

Total      41,352

X36

в

да

	Node 4
	Category	%	n
■	1.0	100,0	11
■	2.0	0,0	0
■	3.0	0,0	0
	Total	8,7	11

да                     нет

X12

<= 3222,00

Node 8
Category	%	n
■ 1.0	0,0	0
2.0	45,5	15
3.0	54,5	18
Total	26,2	33
_ 1 J

норма

выкидыш; аборт

Node 10
Category	%	n
■ 1.0	6,7	2
2.0	43,3	13
3.0	50,0	15
Total	23,8	30
1 II 1

Node 11		n
Category	%
1.0	50,0	5
2.0	10,0	1
3.0	40,0	4
Total	7,9	10

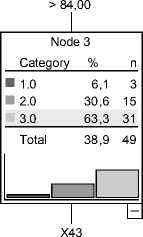
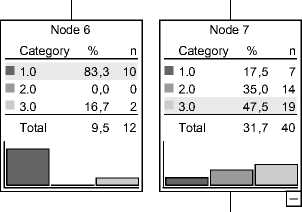
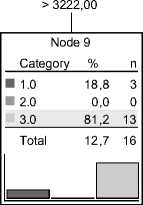
Рис. 3. Дерево классификации (б)

Кроме того, в этом возрастном интервале в случае отсутствия инфицирования ( X 36 = нет) значимое влияние оказывает переменная X 12 – течение предыдущей беременности.

Здесь же можно наблюдать пример объединения двух категорий, схожих по значению прогнозируемого показателя, в одну.

Для иллюстрации объединения категорий построим таблицу сопряженности переменных Уровень ИМ (УИМ) и X 12 для подмножества, соответствующего данному узлу деления (табл. 3).

Таблица 3

Таблица сопряженности для переменных УИМ и X 12. Три категории X 12

		Течение предыдущей беременности X 12			Всего человек
		выкидыш	аборт	норма
к	1	0,33	0,57	0,07	7
	2	0,00	0,14	0,43	14
	3	0,67	0,29	0,50	19
Всего человек		3	7	30	40

Таблица 4

Таблица сопряженности для переменных УИМ и X 12. Две категории X 12

		Течение предыдущей беременности X 12		Всего человек
		выкидыш; аборт	норма
к	1	0,50	0,07	7
	2	0,10	0,43	14
	3	0,40	0,50	19
Всего человек		10	30	40

В ячейках таблицы указаны частоты совместного наблюдения соответствующих категорий.

Следует отметить, что если бы деление в узле было произведено в соответствии с тремя категориями X12, то численность подмножеств составила бы 3, 7 и 30 человек. Для данной задачи был выбран критерий остановки роста дерева – минимальное количество случаев в подмножестве N _min = 10 . Соответственно, в такой категоризации переменная X 12 не вошла бы в число значимых факторов. Объединение первых двух категорий в одну способствовало увеличению представительности подмножеств и позволило зарегистрировать негативное влияние категорий «выкидыш» и «аборт» данной переменной на уровень ИМ. В табл. 4 приведены частоты, соответствующие объединенным категориям.

Кроме того, для пациентов в возрасте X 1 > 84 (мес.) было зарегистрировано существенное влияние на показатель моторики переменной X 43 – вес ребенка (пациента) при рождении. В результате построения дерева классификации в данном узле было выделено два подмножества пациентов (см. рис. 3). Оба подмножества характеризуются высоким значением уровня индекса моторики. Однако для представителей второго подмножества ( X 43 > 3222 (г)) процент случаев со значением уровня ИМ = 3 больше.

Классифицирующие правила для данного узла:

если X 1 > 84 и X 43 <= 3222, то уровень ИМ = 3 с вероятностью 54,5%;

если X 1 > 84 и X 43 > 3222, то уровень ИМ = 3 с вероятностью 81,2%.

Кроме этого, первому подмножеству пациентов соответствует также высокий процент случаев со средним уровнем ИМ = 2:

если X 1 > 84 и X 43 <= 3222, то уровень ИМ = 2 с вероятностью 45,5%.

Полученная закономерность согласуется с оценками медицинских экспертов. Действительно, масса новорожденного X 43 <= 3222 (г) соответствует, как правило, случаям недоношенности и (или) задержки внутриутробного развития.

Однако следует заметить, что во втором подмножестве, характеризуемом в целом высоким уровнем ИМ, присутствует небольшой процент (18,8%) пациентов, у которых наблюдается значение уровня ИМ = 1.

Данная закономерность подтверждает существование негативного влияния высокой массы при рождении на последующее формирование двигательных навыков у больных ДЦП. Одним из объяснений этого явления служит высокая вероятность получения родовых травм в случаях, если масса новорожденного намного превосходит значение X 43, считаемое оптимальным в медицинской практике.

Заключение

Метод деревьев решений представляет собой эффективный инструмент обработки медико-биологических данных, что было подтверждено применением данного метода при прогнозировании двигательного развития больных детским церебральным параличом.

В результате исследования выявлены отдельные факторы и их совокупности, оказывающие наиболее значимое влияние на процесс формирования моторных навыков у больных ДЦП.

В частности, обнаружено, что существенное влияние у больных в возрасте от 5 до 8 лет оказывает показатель кардиограммы, характеризующий степень напряжения механизмов адаптации человеческого организма.

В возрасте старше 7 лет на результате развития двигательных способностей во многом сказывается вес больного при рождении.

Показано, что наличие признаков внутриутробного кислородного голодания или признаков внутриутробного инфицирования больного особенно негативно сказывается при формировании двигательных навыков в возрасте до 4 лет.

В случае отсутствия внутриутробного инфицирования в возрасте от 3 до 7 лет значимым является фактор, характеризующий протекание предыдущей беременности у матери больного (выкидыш / аборт / норма).

Алгоритм поиска значимых факторов метода деревьев решений позволил значительно сократить число входных анализируемых параметров, что является важным в процессе принятия решений при выборе реабилитационной стратегии.

Также были определены диапазоны изменения значимых факторов, соответствующие наиболее высокому уровню развития моторики больных с двигательными нарушениями.

Применение полученных результатов в медицинской практике лечения ДЦП позволит выделить факторы, на которые необходимо оказать воздействие посредством технологий комплексной реабилитации, и установить степень их коррекции для достижения наилучшего двигательного развития больного.

В дальнейшем планируется использование метода деревьев классификации в рамках создания информационно-аналитической системы прогнозирования двигательного развития у детей с церебральным параличом.

Кроме того, представляет интерес дальнейшее изучение медико-биологической природы выявленных зависимостей текущего уровня развития моторных навыков от факторов, провоцирующих появление и характеризующих развитие заболевания ДЦП.