Применение метода «Деревья решений» для дифференциации групп человечества

Высокий фенотипический полиморфизм вида Homo sapiens служит основой для разработки классификаций человечества на разных таксономических уровнях. В настоящий момент созданы десятки таких классификаций по разным системам признаков. Большое количество классификационных схем обусловлено различиями в принципах, на которых они базируются, а также выбором основных и соподчиненных признаков. Авторы многих классификаций стараются придать им филогенетический смысл, чтобы построенная система отражала общность происхождения объектов. Правда, на этом пути существуют неразрешимые проблемы. Типологическое сходство не всегда обусловлено родством, поэтому при построении многих классификаций дополнительно учитываются как географические аспекты распространения признаков, так и внутрипо-пуляционное разнообразие последних, которое отражается в системе внутригрупповых коэффициентов корреляции. Выбор признаков, составляющих основу классификационной схемы, интерпретация морфологического сходства с учетом истории популяций обусловливают субъективизм в классификациях человечества даже на уровне дифференциации больших рас.

Развитие математических методов привело к появлению нового направления в поиске объективной дифференциации – нумерической таксономии, особенностями которой является учет как можно большего числа признаков и допущение их таксономической равноценности. Последнее обстоятельство представляет собой одновременно и достоинство, и основной недостаток любой нумерической классификации. Тем не менее в различных областях биологии этот подход применяется достаточно широко [Sokal, Sneath, 1963, р. 4; Cartmill, 2018; Hugenholtz et al., 2021].

Поиски путей объективной нумерической классификации популяций человечества были начаты еще в работах Е.М. Чепурковского [Tschepourkowsky, 1905], а также активно разрабатывались зарубежными авторами [Morant, 1928; Woo, Morant, 1932; Howells, 1973, р. 149–155, 1990, р. 71–79; Hanihara, 1996, 2000]. В отечественной антропологии разработкой нумерической классификации по краниометрическим признакам занимался В.В. Бунак, предложивший использовать для этих целей три основных диаметра мозгового отдела черепа [1922]. Далее работа в данном направлении продолжилась с привлечением но- вых статистических методов [Алексеев, Трубникова, 1984, с. 1–8, 115–116; Пестряков, Григорьева, 2013]. Но проблема выявления таксономической значимости тех или иных размеров черепа, поиск новых признаков, а также применение различных математических подходов к решению этой задачи по-прежнему не теряют своей актуально сти.

Для построения нумериче ской классификации по размерам черепа используются в основном корреляционные методы, позволяющие интегрировать признаки в более сложные структуры [Алексеев, Трубникова, 1984, с. 1–8, 115–116; Howells, 1990, р. 71–79]. При этом некорреляционных методов в антропологии не так много. Это делает актуальным вопросы их применимости для построения антропологических классификаций и сопоставления результатов, полученных разными методами.

В настоящей работе для создания классификации выборок использован алгоритм «дерево принятия решений» (decision tree), который называют также деревом классификации или регрессионным деревом [Breiman et al., 1984, р. 17; Quinlan, 1986]. Эти названия синонимичны, их употребление зависит от решаемой задачи, т.к. деревья решений можно использовать либо для классификации объектов, либо для построения регрессии. Данный метод, в отличие от канонического дискриминантного анализа, не является корреляционным. Одновременно его математический аппарат не предполагает расчета расстояний между объектами, как в кластерном анализе или многомерном шкалировании. Особенностью алгоритма является также возможность использовать переменные разного типа (количественные и категориальные) в одном наборе. Результаты применения метода достаточно просты и наглядны.

В общем случае дерево представляет собой ветви, которые в определенной точке (узле) дихотомически разделяются, и листья – конечные элементы ветвления. Особенностью алгоритма является отсутствие циклических процессов, поэтому ветви не объединяются, исходное множество объектов разбивается на все более мелкие и все менее разнородные подмножества. В итоге получается график, на котором изображено классификационное дерево с несколькими узлами и конечными результатами разделения – листьями.

На каждом шаге анализа можно оценить дифференцирующую значимость тех или иных размеров и состав получившихся объединений. Очевидно, что группы, разделяющиеся в основании ствола дере- ва, различаются сильнее всего, а наиболее похожие дифференцируются в конечных узлах. Эта информация дает представление о морфологическом сходстве групп и о признаках, которые его обеспечивают. Также отражены пограничные значения этих признаков. Данный метод и обобщающий его алгоритм «случайного леса» широко применяются в различных биологических и медицинских исследованиях [Wong et al., 2004; Djuris J., Ibric, Djuric Z., 2013; Фельдман, 2020; Al Mamun, Keikhosrokiani, 2022].

Материалы и методы

Математический подход, используемый в алгоритме деревьев классификации, основан на поэтапном разделении выборок с максимальным уменьшением меры их разнородности, т.е. на снижении вероятности объединения в некоторой точке выборок, относящихся к разным типам. Дробление продолжается до тех пор, пока в листе дерева не останутся объекты одного типа. Таким образом, необходимость дальнейшей дихотомии определяется критерием разнородности выборок в каждой точке. В качестве такового используют показатель энтропии и индекс Джини. Для нашей задачи мы выбрали первый.

Формула расчета энтропии Шеннона:

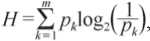
где k – количество типов; p_k – вероятность того, что объект принадлежит к типу k .

Первое ветвление происходит по признаку, по которому различается наибольшее количество выборок, на втором шаге разделяются уже два объединения групп, и так далее, пока не останутся гомогенные наборы образцов. В результате можно составить представление о том, какие из используемых признаков наиболее значимы при дифференциации конкретных объектов. Разделение происходит на основе дискретности вариационного ряда средних значений.

Применяемый алгоритм дерева решений является частью более общего метода, называемого «слу- чайный лес» (random forest). Его суть также состоит в построении классификационных или прогностических деревьев. Но в алгоритме случайного леса предполагается предварительный этап машинного обучения, при котором создаются обучающая и тестовая выборки. Построение единичного дерева имеет определенные ограничения: нельзя гарантировать, что алгоритмом был выбран оптимальный путь. Однако для дифференциации групп по средним значениям признаков такой метод подходит. При этом прогностическое значение классификации не является ключевым, а получаемый результат нагляден и прост для интерпретации. Алгоритм классификационных деревьев реализовывался с помощью библиотеки scikit-learn в языке Python [Pedregosa et al., 2011].

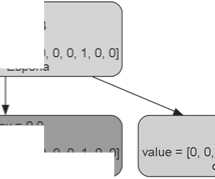
Каждый узел (лист) дерева содержит несколько параметров дифференциации (рис. 1):

• 1)    абсолютное значение того признака, который разделяет две совокупности на конкретном шаге; меньшее значение имеют группы, расположенные на рисунке слева от узла, большее – справа;

• 2)    величину энтропии Шеннона ( H ) для выборок, разделяемых на данном уровне (entropy);

• 3)    число групп ( y ), которые составили совокупности на данном этапе разделения (samples = n ( y ));

• 4)    количество выборок в каждом классе – сформированной нами региональной группе (value = [ n ₁, n 2 , n 3 , … n k ]);

• 5)    преобладающий на данном этапе дифференциации класс, т.е. тот, в котором больше всего групп (class = макрорегиональная группа).

В работе использованы 15 краниометрических признаков, соответствующих стандартной методике [Martin, 1928, S. 625–660; Алексеев, Дебец, 1964, с. 52–74] (обозначены согласно нумерации в программе Р. Мартина): продольный диаметр (М.1), поперечный (М.8), высотный (М.17), длина основания черепа (М.5), наименьшая ширина лба (М.9), лобная дуга (М.26), теменная (М.27), затылочная (М.28), скуловой диаметр (М.45), средняя ширина лица (М.46), длина основания лица (М.40), верхняя высота лица (М.48), высота носа (М.55), ширина носа (М.54), высота орбиты (М.52).

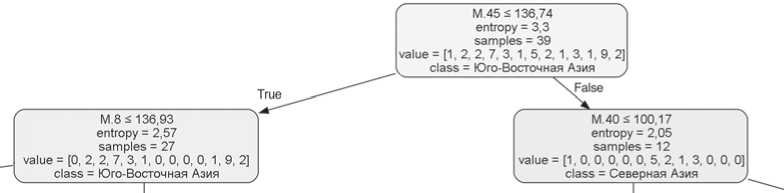
Рис. 1. Первый шаг анализа при дифференциации по линейным размерам.

Исходный набор из 39 групп получил название «Юго-Восточная Азия», т.к. эти выборки наиболее многочисленны. Информационное содержание каждого узла описано в тексте.

Для построения классификации использовались средние значения по 39 этнотерриториальным группам из 13 макрорегионов Старого Света (см. таблицу). Данные взяты из литературных источников, часть черепов измерена одним из авторов в фондах НИИ и Музея антропологии МГУ, Музея антропологии и этнографии им. Петра Великого. Использовались данные только по мужским черепам.

Список используемых в анализе групп и их географическая принадлежность

№ п/п	n	Группа	Источник	Регион
1	11	Тейта	[Kitson, 1931]	Восточная Африка
2	39	Тигре	[Sergi, 1912]
3	88	Камерун	[Drontschilow, 1913]	Центральная Африка
4	24	Баски	[Morant, 1929]	Европа
5	10	Болгары	Данные О.А. Федорчук
6	14	Итальянцы	То же
7	63	Армяне	[Бунак, 1927]
8	9	Ирани	Данные О.А. Федорчук
9	15	Латыши	То же
10	56	Осетины	»
11	11	Чукчи	»	Северная Азия
12	18	Эскимосы Чукотки	»
13	11	Алеуты	»
14	93	Эскимосы Аляски	[Дебец, 1986]
15	11	Якуты	Данные О.А. Федорчук
16	109	Казахи	[Исмагулов, 1970]	Средняя Азия
17	9	Киргизы	Данные О.А. Федорчук
18	61	Ханты	То же	Западная Сибирь
19	26	Теленгиты	»	Центральная Азия
20	154	Буряты	Архивные данные Н.Н. Мамоновой (предоставлены Д.В. Пежемским)
21	17	Монголы	Данные О.А. Федорчук
22	7	Айны	То же	Дальний Восток
23	36	Непальцы	[Morant, 1924]	Восточная Азия
24	32	Тибетцы	[Ibid.]
25	22	Аэта	[Bonin, 1931a]	Юго-Восточная Азия
26	19	Бантам	[Ibid.]
27	25	Джакарта	»
28	28	Даяки	»
29	14	Мадура	»
30	28	Яванцы	»
31	15	Тагалы	»
32	32	Средняя Ява (сборная)	»
33	44	Бирманцы	[Tildesley, 1921]
34	15	Андаманцы	[Bonin, 1931a]	Южная Азия
35	35	Тамилы	[Harrower, 1924]
36	49	Новая Британия	[Bonin, 1936]	Меланезия
37	72	Сев. Новая Гвинея	[Hambly, 1940]
38	25	Юж. Новая Гвинея	[Ibid.]
39	24	Остров Пасхи	[Bonin, 1931b]	Полинезия

Примечание. Макрорегиональные группы сформированы с учетом только географической принадлежности.

Результаты

При анализе линейных размеров на первом шаге дифференциация происходит по скуловому диаметру (М.45) (рис. 1). Выборки Центральной, Северной, Средней Азии, а также айны и ханты имеют бóльшие значения этого признака (более 136,74 мм). Они со- ставили группу из 12 выборок, получившую на данном этапе название «Северная Азия». Более узкое лицо характерно для выборок Юго-Восточной, Южной и Восточной Азии, Европы, Африки, Меланезии и Полинезии, эта смешанная группа названа по самому многочисленному классу «Юго-Восточная Азия». В нее вошло 27 выборок.

Рассмотрим дальнейшую дифференциацию в под-

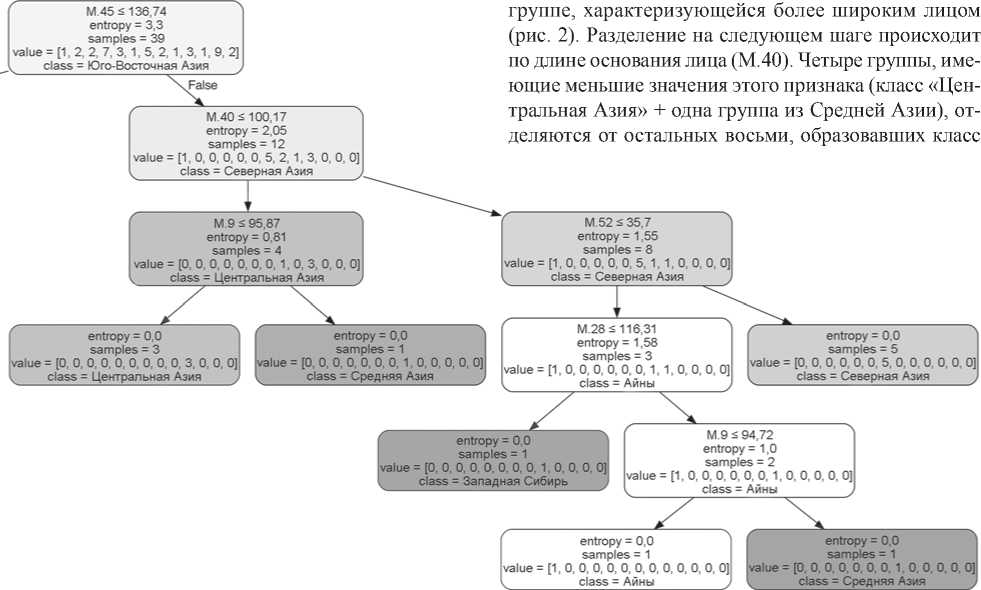
Рис. 2. Ветвь дерева для групп с бóльшим скуловым диаметром после первой дихотомии (градации серого обозначают преобладание групп из той или иной макрорегиональной группы в узле или листе).

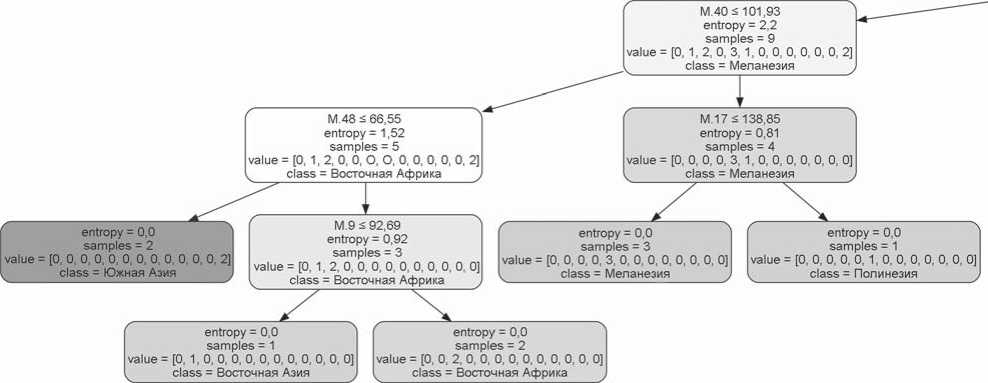
Рис. 3. Ветвь дерева для групп с меньшим

«Северная Азия», в который также вошли ханты Западной Сибири и айны.

Нулевое значение показателя энтропии для класса «Центральная Азия» достигается уже на следующем шаге, а для разделения класса «Северная Азия» на однородные группы потребовалось еще три, в которых использовались значения признаков М.52 (высота орбиты), М.28 (затылочная дуга) и М.9 (наименьшая ширина лба). В итоге получили листья дерева – однородные классы, содержащие только выборки одного макрорегиона: «Центральная Азия» (три выборки), «Западная Сибирь» (одна выборка), «Айны», «Северная Азия» (пять выборок). Выборки казахов и киргизов, отнесенные нами к региону «Средняя Азия», разделились на два отдельных блока. Любопытно, что на финальных этапах обе отделились от «похожих» групп за счет бóльшей ширины лба (М.9). А разнесение среднеазиатских выборок по разным ветвям связано с их различиями по длине основания лица.

Групп, которые после первой дихотомии отделились как более узколицые, больше, показатель энтропии для этого набора выше, поэтому дифференциация потребовала большего числа шагов (рис. 3). На втором шаге дифференцирующим признаком для них выступает поперечный диаметр черепа (М.8). Затем для одной из ветвей значимой является ширина лба (М.9). По этому признаку азиатские выборки отделяются от объединения европейских и центральноафриканской. Получение однородных классов на заключительном этапе происходит по высотным размерам – М.48 (высота лица) и М.55 (высота носа). Финальная дифференциация популяций разных макрорегионов самой левой ветви дерева (рис. 3) идет по очень сходному набору признаков: длине основания лица (М.40), высоте черепа (М.17), высоте лица (М.48) и наименьшей ширине лба (М.9).

Обсуждение

Первый вопрос – насколько представленная с помощью дерева решений дифференциация соответствует какой-либо антропологической классификации. Второй вопрос – какие признаки стали основой разделения общего набора на однородные группы.

Первая дихотомия по скуловому диаметру соответствует представлениям о значимости этого признака для классификации. Действительно, большинство североазиатских групп монголоидной расы отличаются высокими значениями ширины лица. Поэтому первая дихотомия логично разделяет северных и южных, более грацильных монголоидов. К последним присоединяются и другие выборки с малой шириной лица – африканские, европейские, восточно- и южноазиатские, а также группы Океании. Этот второй

M 8 < 136,93 entropy = 2,57 samples = 27 value = (0, 2, 2, 7, 3, 1, 0, 0, 0, 0, 1, 9, 2] class = Юго-Восточная Азия ,

entropy = 0,0

samples = 9

value = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 9, 0]

. class = Юго-Восточная Азия .

M 48 *72,15 entropy = 0,47 samples = 10 value = (0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 9, 0) class = Юго-Восточная Азия .

M 9*94,84 entropy =1,49 samples =18 value = (0,1, 0, 7, 0, 0, 0, 0, 0, 0,1, 9, 0] . class = Юго-Восточная Азия ,

entropy = 0,0

samples = 1

value = (0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

, class = Восточная Азия .

value =[1,2, 2, 7, 3, 1,5, 2, 1, 3, 1,9, 2)

M 45 s 136 74 entropy = 3,3

M 55 s 49,73 entropy =0,54 samples = 8 value = [0, 0, 0, 7, 0, 0, 0, 0, i           class = Европа

entropy = 0,0

samples = 7

0, 7, 0, 0, 0, 0, 0, 0, 0, 0, 0] class = Европа

entropy = 0,0 samples = 1 value = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0] class = Центральная Африка

скуловым диаметром после первой дихотомии.

кластер состоит из разнородных групп, однако его дальнейшее дробление приводит ко все более полному соответствию полученной картины антропологической классификации, что вполне объяснимо, т.к. любая система учитывает и ареал популяций. Интерес представляют те региональные объединения, которые разошлись по разным ветвям дерева. Их два – среднеазиатское, о котором говорилось выше, и восточноазиатское – непальцы, тибетцы. Подчеркнем, что оба случая связаны с дифференциацией выборок, ареал которых приходится на зону контакта разных подразделений человечества: среднеазиатские группы относятся к метисной южносибирской расе, а восточноазиатские происходят из региона на стыке территорий распространения малых рас, относящихся к большой монголоидной расе.

Признаки, по которым происходят дихотомические деления, во многом повторяются в узлах разного уровня, что говорит об их значимости. Большинство этих признаков традиционно используются для классификации популяций. Но есть и такие, значимость которых неочевидна, например длина основания лица (М.40) или ширина лба (М.9).

Сравним результаты, полученные с помощью алгоритма деревьев решения и широко применяемым методом многомерного шкалирования (рис. 4), для которого использована матрица расстояний Эвклида. Коэффициенты алиенации и стресса составили соответственно 0,117 и 0,108.

Расположение групп на координатном поле соответствует классификации, полученной с помощью дерева решений. Хорошо видно, что часть выборок, относящихся к Северной, Центральной и Средней Азии (обведены овалом), заметно обособилась от остальных. Зная результаты анализа дерева клас- сификации, можно утверждать, что увеличение расстояния между этим кластером и всеми остальными группами произошло благодаря различиям по скуловому диаметру (М.45). На краю кластера располагается и выборка айнов. В целом его состав абсолютно соответствует правой ветви дерева классификации (см. рис. 2).

Не менее показательно и второе, весьма рыхлое объединение выборок. Его состав совпадает с левой ветвью дерева решений (см. рис. 3). Так же в одном подмножестве объединились выборки Европы, Юго-Восточной Азии, к ним примкнули краниологические серии Восточной Азии и Центральной Африки. Ориентируясь на результаты анализа дерева классификации, можно уверенно говорить, что данная искусственная совокупность возникает на фоне сходства по ширине мозгового отдела (М.8). А разделение этих разнородных групп возможно на основании наименьшей ширины лба (М.9), что хорошо видно на дереве решений. Причем данный метод позволяет разделить их полностью, в то время как на графике многомерного шкалирования две выборки Южной Европы (ирани и армяне) попадают в кластер Юго-Восточной Азии.

Наконец, по периферии поля многомерного шкалирования расположились группы, которые в рамках дерева классификации составили самую левую ветвь, объединившую выборки Меланезии, Полинезии (о-в Пасхи), Восточной Африки, Южной Азии и одну из Восточной Азии (непальцы). Судя по расположению этих групп на графике, в реальности они очень различны. Так, выборки андаманцев и аборигенов о-ва Пасхи довольно сильно отделены от основного массива, что соответствует их особому антропологическому статусу.

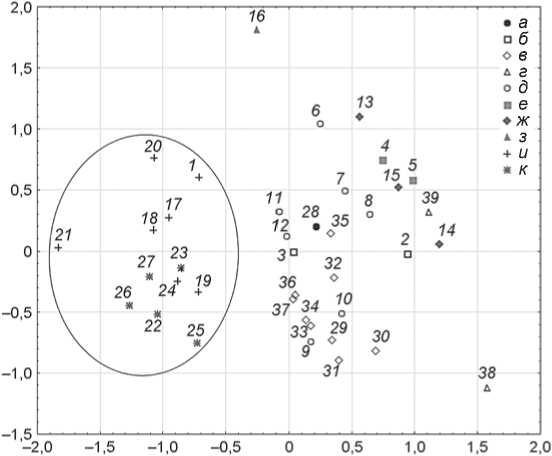
Рис. 4. Дифференциация групп по результатам многомерного шкалирования.

1 – айны; 2 – непальцы; 3 – тибетцы; 4 – тэйта; 5 – тигре; 6 – баски; 7 – болгары; 8 – итальянцы; 9 – армяне; 10 – ирани; 11 – латыши; 12 – осетины; 13 – Новая Британия; 14 – Сев. Новая Гвинея; 15 – Юж. Новая Гвинея; 16 – о-в Пасхи; 17 – чукчи; 18 – эскимосы Чукотки; 19 – алеуты; 20 – эскимосы Аляски; 21 – якуты; 22 – казахи; 23 – киргизы; 24 – ханты; 25 – теленгиты; 26 – буряты; 27 – монголы; 28 – Камерун; 29 – аэта; 30 – Бантам; 31 – Джакарта; 32 – даяки; 33 – Мадура; 34 – яванцы; 35 – тагалы; 36 – Средняя Ява (сборная); 37 – бирманцы; 38 – андаманцы; 39 – тамилы.

а – Центральная Африка; б – Восточная Азия; в – ЮгоВосточная Азия; г – Южная Азия; д – Европа; е – Восточная Африка; ж – Меланезия; з – Полинезия; и – Северная Азия; к – Средняя и Центральная Азия.

Заключение

Дифференциация человечества на группы только по линейным размерам черепа неизбежно имеет ограничения: в разных регионах земли дифференцирующие признаки отличаются. Поэтому попытка разделить значительный массив выборок с использованием небольшого набора признаков не вс егда может быть успешной. Однако возможности метода деревьев решений оказались достаточными, чтобы построить классификацию, соответствующую классическим представлениям о дифференциации человечества. С помощью этого метода нельзя оценить величину расстояний между отдельными группами, однако он позволяет выявить признаки, по которым происходит дихотомия выборок вплоть до финального этапа. Направления межгрупповой морфологической изменчивости могут быть определены посредством канонического дискриминантного анализа, но он относится к числу корреляционных методов, а значит, существуют ограничения на использование в одном наборе исходных признаков и индексов на их основе, а также категориальных признаков. Деревья классификации дают возможность работать как с категориальными признаками, так и с индексами. Таким образом, арсенал антропологических методов классификации пополнился еще одним инструментом, который позволяет получить новую информацию и использовать разные наборы признаков. Можно рекомендовать применение алгоритма деревьев принятия решений как независимого метода систематики на внутривидовом уровне.

Исследование выполнено в рамках исследовательской темы «Формирование некоторых морфо-функциональных особенностей человека в фило- и онтогенезе» кафедры антропологии МГУ и Государственного задания Медико-генетического научного центра им. академика Н.П. Бочкова.