Применение метода функций Грина для решения пространственно одномерных задач теории сушки электромагнитным излучением

С точки зрения математической физики основной проблемой теории электромагнитной сушки является построение алгоритмов для совместного решения уравнений тепломассопереноса и уравнений электромагнитного поля в условиях, когда заданы геометрия образца, параметры обтекающего его воздушного потока, теплофизические и электромагнитные характеристики материала, из которого этот образец состоит, условия возбуждения электромагнитного поля в той области, где располагается образец. В такой постановке эта проблема исследовалась авторами в [1–4]. Здесь мы ограничимся ситуацией, когда распределение источников тепла, вызванных поглощением энергии электромагнитных волн, считается наперед заданным и требуется построить совместное решение лишь для двух связанных уравнений параболического типа, моделирующих распространение тепла и влаги сквозь пористую среду. Эта задача может быть решена численно, с использованием стандартных конечно-разностных процедур, однако такой важный в математической физике расчетный метод, как метод разделения переменных (метод Фурье), обладающий, в отличие от численных методов, возможностями аналитического исследования процесса, в данном случае применен быть не может. Во-первых, это обусловлено тем

существенным обстоятельством, что задачи теории сушки в большинстве случаев ставятся как нелинейные . Во-вторых, в задачах сушки мы всегда имеем систему из нескольких искомых функций, в то время как в методе Фурье речь идет о начальнокраевых задачах для одной искомой функции переменной точки и времени. Эта вторая причина является серьезным препятствием, поскольку, как известно, из системы дифференциальных уравнений в частных производных, в отличие от системы обыкновенных дифференциальных уравнений, в общем случае нельзя получить отдельные уравнения для каждой из искомых функций [5]. Указанные проблемы могут быть решены с помощью алгоритма расщепления процесса по физическим факторам. Идея расщепления, но примененная к проблеме распространения загрязнений в окружающей среде, обсуждалась в работе [6]. На основе этой идеи авторами разработан и применен для исследования задач сушки оригинальный расчетный алгоритм, использующий метод Фурье и аппарат функций Грина [7]. Однако в указанной работе излагалась лишь общая схема расчета, примененная к неоднородному телу произвольной формы . Здесь на примере сушки однородной пластины мы покажем, каким образом эти расчеты могут быть доведены до конца. Задача о сушке пластины рассматривалась многими авторами, и для нее к настоящему времени построены решения анали-

ЕЛ^М © Афанасьев А.М., Сипливый Б.Н., 2020

тические [8; 9], численные [10; 11] и асимптотические [12; 13]. Развиваемый в настоящей статье подход позволит говорить о новом типе решений, в котором содержатся элементы всех трех перечисленных выше типов.

Постановка начально-краевой задачи

Схема сушки плоского образца показана на рисунке. Влажный образец обдувается воздушным потоком и подвергается воздействию плоских электромагнитных волн двух видов, с малой и с большой глубиной проникновения, которые индуцируют источники тепла, распределенные, соответственно, по поверхности образца и по его объему.

Условие тепло- и влагоизоляции нижней поверхности пластины означает, что исходным объектом изучения является пластина толщиной 2 d , у которой вследствие идентичности краевых условий и условий облучения на поверхностях x = 0 и x = 2 d отсутствуют тепловые потоки и потоки влаги сквозь плоскость симметрии x = d .

Образец состоит из двух компонентов: твердой основы (капиллярно-пористое тело) и воды. В качестве математической модели распространения тепла и влаги сквозь пористую среду будем использовать подход, принятый в теории тепломассо-переноса А.В. Лыкова. Исходные приближения имеют следующий вид.

• а)    В отношении всех физических свойств материал пластины предполагается однородным.

• б)    Толщина пластины 2 d является малой по сравнению с ее размерами в направлениях, перпендикулярных оси x .

• в)    Плотность поверхностных источников тепла S , вызванных поглощением излучения с малой глубиной проникновения, а также интенсивность теплообмена Q и интенсивность массообмена J поверхности x = 0 с воздушной средой слабо изменяются вдоль этой поверхности, т. е. эти величины зависят только от времени t .

• г)    Плотность внутренних источников тепла W , вызванных поглощением проникающего электромагнитного излучения, зависит только от координаты x и времени t .

При сделанных предположениях распределения температуры Т и влагосодержания U будут зависеть только от x и t , т. е. искомыми функциями будут Т ( x , t ) и U ( x , t ). Уравнения распространения тепла и влаги и краевые условия тепло- и массо-обмена на границах x = 0 и x = d будут иметь следующий вид [14–16]:

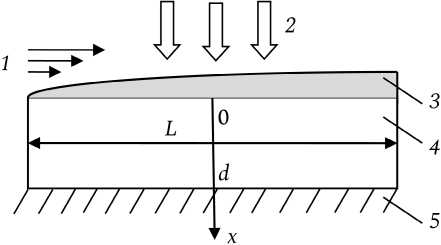
Рис. Схема электромагнитной сушки: 1 – воздушный поток; 2 – плоская электромагнитная волна; 3 – пограничный слой; 4 – пластина из влажного материала; 5 – тепло- и влагоизоляция Fig. The scheme of electromagnetic drying: 1 – air flow; 2 – plane electromagnetic wave; 3 – boundary layer; 4 – plate of wet material; 5 – heat and moisture insulation

• 8 T  , 82 T ,

с р— = к —— + r ур---+ W ( x , t ) , 0 <  x <  d ;

81     8x2        8t

• 8 U     8 2U.8

— = a m”Г ⁺ a m ⁵-y , ⁰ <  ^x<  d ;

• 8 t       8 x 2

Q ⁽ t ^{) +} r ^{( 1} -^ J ( t ⁾ = k | T ⁽ 0, t ) ⁺ S ⁽ t ⁾ , ^x = 0;

^{J (} t ^{) =} a m P^ U ⁽ 0, t ^{) +} a m P ⁶^ ⁽ 0, ^T) ’ x = 0;

• —( d , t ) = 0, U-(d , t ) = 0, x = d ;

8x8

^T ( x ,0 ) = ф _T ( x ) , U ( x ,0 ) = ф и ( x ) , 0 <  x <  d , t = 0.

Здесь с, p, k, у, am, б - теплофизические характеристики материала, а именно удельная теплоемкость, плотность в сухом состоянии, коэффициент теплопроводности, критерий испарения, коэффициент диффузии влаги, относительный коэффициент термодиффузии влаги; r - удельная теплота парообразования воды; фT(x) и фU(x) - заданные функции, определяющие распределения температуры и влагосодержания в начальный момент времени t = 0. Интенсивности тепло- и массообмена поверхности образца с воздушной средой Q и J однозначно определяются температурой поверхности Т(0, t) и рассчитываются по формулам:

Q ( t ) = а A ( T ( 0, t ) + T i ) ⁴ - ( T _B + T i ) 4

+

+ a _w [ T ( 0, t ) - T B ] ;

J ( t Hm [ ^P ( ^T (°, t ) ) -Y ^P ( T B ) ] ;

P ( T ) = 6,03 • 10 ^{- 3} exp—---;

T + T 2

^a w = ^k w L^ ’ ^a m = k m L^ >                    (⁹⁾

k w = 3,82

Вт ■ с' .

2        ’

М ■ С

к _ш = 2,54 ■ 10 ^{- 3}

КГ с¹ / ² ■ м ² .

Расщепление задачи по физическим факторам

В этих формулах: ст - постоянная Стефана -Больцмана; A - коэффициент теплового излучения; Т _в и v - температура и влажность воздуха за пределами пограничного слоя; a w и a m - коэффициенты тепло- и массообмена поверхности образца с воздушной средой; Р ( Т ) - функция, моделирующая зависимость относительного парциального давления насыщенного водяного пара от его температуры Т при общем нормальном давлении; Т 1 = 273 ° С и Т 2 = 238 ° С - постоянные. Если заданы скорость воздуха вне пограничного слоя V и длина пластины в направлении движения воздуха L , то при ламинарном состоянии пограничного слоя коэффициенты a _w и a _m можно рассчитать по формулам (9), полученным авторами в работе [15]. Коэффициенты k _w и k _m соответствуют средним по толщине пограничного слоя температуре Т ср = 50 ° С и влажности ф _ср = 0,7. Условие ламинарного состояния пограничного слоя имеет вид VL < 9,05 м²/с.

Система двух связанных параболических уравнений (1) и (2) моделирует процессы распространения тепла и влаги сквозь пористый материал. Краевые условия (3) и (4) имеют смысл баланса потоков тепла и влаги на поверхности x = 0. Входящая в эти формулы интенсивность теплообмена Q , согласно (7), включает теплообмен конвекцией и теплообмен излучением; интенсивность массообмена J , согласно (8), принимается в виде закона испарения Дальтона. Формулы (5) определяют краевые условия на поверхности x = d и выражают факт ее тепло- и влагоизоляции.

Начальные и граничные условия сформулированной задачи должны быть согласованы . Это означает, что уравнения (3)–(5) должны выполняться при подстановке в них на место функций Т ( x , t ) и U ( x , t ) соответственно функций ф _т ( x ) и ф у ( x ), причем функции Q ( t ) и J ( t ) в (3) и (4) должны быть предварительно вычислены по формулам (7), (8), где на место Т (0, t ) следует подставить ф _т (0). Если условие согласования не выполнено, то задача не имеет ни физического смысла, ни классического решения. Тем не менее такая задача может считаться поставленной корректно, если можно будет построить ее обобщенное решение , которое при t ^ 0 будет примыкать в среднем к начальным распределениям ф т ( x ) и ф у ( x ). Эти вопросы обсуждаются в [17-19].

Начав с момента t = 0, будем решать поставленную задачу на малом интервале времени 0 <  t <  A t . Пользуясь заданным начальным распределением температуры ф _т ( x ), вычислим при t = 0 второе слагаемое в правой части уравнения (2) и обозначим результат, как показано ниже:

а _ш 8д ² T ( х ,0 )/ д х ² = a _ш 8 d ² ф _т ( х )/ dx ² ^ f U ( x ) .

Подставив это выражение в (2), получим для поля влагосодержания U следующее уравнение параболического типа:

д U /д t = а _ш д ² и /д х ² + f U ( х ) .

Это уравнение является приближенным, так как мы не учитываем изменение во времени производной д ² т /д х ². Исходя из того же начального распределения температуры ф _т ( x ) и рассматривая его при х = 0, т. е. используя величину ф _т (0), найдем с помощью (7) и (8) интенсивности тепло- и массо-обмена Q и J на поверхности пластины в начальный момент t = 0:

Q ( О ) = СТ А ( ф т ( О ) + ^ ) ⁴ - ( ^т _в + ^ ) ⁴

+

+ a w [ф т ( ⁰ ) - ^т в > Q ⁰ ;

J ( 0 Н [ P ( ф т «») -Ф P ( ^т в )> J ⁰.

Теперь из краевых условий (3) и (4) могут быть определены нормальные производные полей Т и U на границе x = 0 в тот же самый момент t = 0: д т /д х ( 0,0 ) = [ Q ⁰ + Г ( 1 - Y ) J ⁰ - S ( 0 ) ] [к = ц _т ;

д и / д x ( 0,0 ) = J ⁰ /( а ш Р ) -8ц т i u .

Возвратившись к полю U(x, t), пренебрежем на нашем малом интервале 0 < t < At изменением во времени нормальной производной дU/дx на границе x = 0. Тогда для нахождения этого поля получим следующую начально-краевую задачу: 'д и/ д t = аш д2и/ дх2 + fu (х), 0 < х < d, 0 < t < At;

д и / д х ( 0, t ) = ц _и ; д и / д х ( d , t ) = 0;

^u ( ^{x ,0} ) = ф у ( ^x ) .

Это задача Неймана для неоднородного уравнения параболического типа с неоднородными краевыми и начальными условиями. Процедура решения этой задачи методом Фурье будет рас- смотрена ниже. Используя найденную функцию U(x, t), вычислим во всех точках x производную ∂U/∂t при t = 0 и обозначим

[ r YP d U /d t ( x ,0 ) + W ( x ,0 )]/( c p ) = f T ( x ) .

Тогда, пренебрегая изменением во времени последних двух слагаемых в правой части (1), а также изменением производной ∂ Т /∂ x на границе x = 0, получим для нахождения поля температуры Т ( x , t ) задачу Неймана, аналогичную той, которая получена была выше для поля влагосодержания:

s т / a t = a w -a ² т/ a X ² + f T ( X ) ,

0 <  x <  d , 0 <  t < A t ;

'                                                                (11)

a т /a x ( 0, t ) = ц _T ; a т /a x ( d , t ) = 0;

_ ^T ( ^{x ,0} ) = Ф T ( ^x ) .

Здесь a _w = kJ ( c p ) - коэффициент диффузии тепла (коэффициент температуропроводности).

Решив задачу (11) методом Фурье, найдем поле температуры как функцию координат и времени.

Таким образом, здесь мы построили процедуру расщепления , или развязывания , общей начальнокраевой задачи (1)-(9) для двух функций Т и U , непосредственное исследование которой методом Фурье произведено быть не может, на две отдельные задачи для этих функций, задачи (10) и (11), к которым метод Фурье уже вполне может быть применен. Подчеркнем, что решения этих задач будут приближенно описывать поведение полей U ( x , t ) и Т ( x , t ) лишь вблизи начального момента t = 0. Получить из исходной системы (1)-(9) отдельные начально-краевые задачи для этих двух полей, решения которых давали бы их описания в любой момент времени, оказывается невозможным.

Выше были построены распределения U ( x , t ) и Т ( x , t ). Их справедливость ограничена малым интервалом времени 0 <  t <  A t . Вычислим функции координат U ( x , A t ) и Т ( x , A t ). Объявив их начальными распределениями и повторив изложенный выше алгоритм расчетов, найдем новые функции координат U ( x , 2 A t ) и T ( x , 2 A t ) в момент t = 2 A t и т. д., вплоть до некоторого заданного момента окончания расчетов, чем и будет завершена процедура построения решения сформулированной задачи.

Задача Неймана для уравнения диффузии

Общий вид сформулированных нами начальнокраевых задач (10) и (11) может быть представлен следующим образом:

a у/ a t = a s^y/ a x ² + f ( x ) ,

0 <  x <  d , 0 <  t < A t ;

'                                                                (12)

a Y / a x ( 0, t ) = ц 1 ; a у/ a x ( d , t ) = ц ₂;

^Y ( ^{x ,0} ) =ф ( ^x ) .

Это пространственно одномерная задача Неймана для уравнения диффузии в однородной среде. Здесь а - коэффициент диффузии; f ( x ) и ф ( x ) -заданные функции; щ и р₂ - заданные числа; Y ( x , t ) – искомая функция.

В принципиальном плане алгоритм построения решений таких задач, и даже при более общих условиях f = f (x, t), Ц1 =Ц1 (t), Ц2 = ^2 (t), является в математической физике известным [18]. Нашей задачей будет привести известные в литературе общие теоретические результаты к виду, пригодному для выполнения конкретных в данном случае расчетов. Попытки такого рода предприняты, например, в [20], где анализ производится операторным методом. Здесь мы построим решение другим методом, использующим собственные функции задачи Штурма – Лиувилля и аппарат функций Грина. Такой подход кроме преимуществ, о которых будет сказано ниже, позволит еще распространить предложенный алгоритм исследования задач сушки на образцы с произвольной геометрией. Опираясь на [18], приведем необходимые сведения из теории решения начально-краевых задач и осуществим необходимые для дальнейшего вычисления.

Решение исходной задачи (12) для поля Y представляется в виде

Y = Y 1 + Y 2 + Y 3 ,                                  (13)

где стоящие в правой части функции находятся как решения других, имеющих более простой вид и представляющих, кроме того, и самостоятельный интерес, начально-краевых задач:

a Y 1 /St = a a ² Y1 ^x ²;

< a Y 1 [S x ( 0, t ) = 0; a Y 1 ^ x ( d , t ) = 0;                 (14)

• ^Y 1 ( ^{x ,0} ) = ф ( ^x ) .

'a Y 2/ a t = a a ² Y 2/ a x ² + f ( x ) ;

< a Y 2 /a x ( 0, t ) = 0; a Y 2 /a x ( d , t ) = 0;                 (15)

• Y 2 ( x ^,0 ) = 0.

d Y3^t = a 5 2 Y3/ d x 2 ;

• < 8 Y 3 jdx ( 0, t ) = Цр d Y 3 ^8x ( d , t ) = Ц 2 ;

Y 3 ( x ,0 ) = 0.

Решения задач (14) и (15) для Y ₁ и Y ₂ следующим образом:

d

• Y 1 ( x , t ) = j G ( x , t , x ') ф ( x ') dx ';

0 td

выглядят

Y 2 ( ^x, t ) = jj G ( ^x, t

^^^^^^»

т , x ') f ( x ') dx 'd t .

Здесь G ( x , t , x ') - функция Грина исходной задачи (12) для поля Y . К этому понятию мы вернемся позже. Что же касается задачи (16) для Y ₃, то ее решение ищется в виде

• ^Y 3 = ^Y + ^Y ,

где Y - новая искомая функция, а функция Y подбирается так, чтобы в задаче для Y краевые условия получились бы однородными . Метод подбора такой функции Y в случае задачи Дирихле описан в [17]. Применив этот метод к задаче Неймана (16) для поля Y ₃, получим, что

• ^Y ( ^Х ) = ^Ц 1 ^Х + ^ 2 2d^^{1 Х} 2 .

Учитывая такое выражение для Y , и подставляя функцию Y 3 = Y + Y в задачу Неймана (16) для Y 3 , получим для новой искомой функции Y задачу, в которой, как это уже было объявлено выше, краевые условия будут однородными:

8 Y/ 8 t = a 8²y) d x ² + f ;

< 8 Y/ 8 x ( 0, t ) = 0; 8 Y 8 x ( d , t ) = 0;

Y ( x ,0 ) = ^ф ( x ) .

Здесь обозначено f = a (Ц2-Ц1) , f = d ’

ф ( ^Х ) = - Y ( ^Х ) = ^- Ц 1 ^x -^р ^Х 2 .

Очевидно, что решение задачи (18) для Y можно представит в виде

Y = Y1 + Y2, где функции Y1 и Y2 являются решениями задач (14) и (15) для Y^и Y2, в которых ф и f нужно заменить на ф и f. Пользуясь эти утверждением и обращаясь к формулам (17), образуем решения Y1 и Y2, а затем найдем

Y 3 = Y 1 + Y 2 + Y .

Результат получится таким:

d       ,Г    ^-^

Y ₃ ( x , t ) = - J G ( x , t , x ') ц₃ x ' + —²----¹ x '² j dx ' +

^J0             ^           ² d ^

+ a ^(ц 2_d^-^) j j G ( x , t

т , x ') dx ' d т +

+ Ц 1 Х +

Ц ₂ -Ц 1

2 d

x ²

Функция Грина задачи Неймана для уравнения диффузии

Функция Грина G (x, t, x') задачи Неймана (12), которая входит в построенные решения (17) и (19), вводится формулой vn ( Х ) vn ( Х ’)

to

G ( x , t , x ') = ^ exp ( -X n at ) n = 0

v n

Здесь X n и v n ( х ) есть собственные числа и собственные функции задачи Штурма – Лиувилля : | d ² v ( x ) / dx ² + X v ( x ) = 0;

| dvjdx ( 0 ) = 0; dvjdx ( d ) = 0.

В формулу для G ( x , t , x ') входит также квадрат нормы собственной функции

d

||v n |^ = j v n ( ^Х ) ^dx .

Построение функции Грина указанного вида произведено в [17]. Она выглядит следующим образом:

1 2

G ( x , t , x ) = d ⁺ d ^ exP n = 1

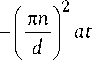
X n n      n n ,

X cos x cos x . dd

Подставим теперь эту функцию в формулы (17) и (19) и выполнив, где это возможно, интегрирование в получившихся выражениях, получим окончательные выражения для функций Y ₁, Y ₂ и Y ₃ . Эти выкладки имеют большой объем; опуская их, приведем лишь результат:

n = 1

1 d            2

Y 1 ( x , t ) = d j ф ( x ) dx ⁺ d ^ exP

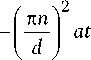
X

n n

X cos —- x d

d jф(x') cos ^nxdlx'

Y 2 ( x , t ) =

d

5 J f ⁽ x ' ) dx'

t +

2 d

⁺ 2 n a

м I z-2- [1 - exp n=1 n I

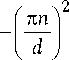
at

n n

X cos x d

d

J f ( x ') cos ^ n x 'dx' 0

Y (x,t) = -d(2^1^^2) + x + ^2Z^1 x2 + 3                6         1      2 d a (^2 —^1) d

2 d 1 Г / xi t - X^ ₂ ^Ц 1 - ^Ц 2 ^{(- 1 )}

ⁿ n = 1 ^{n L}

x exp

n n cos    x.

d

Итак, решение задачи Неймана (12) имеет вид (13), где функции Y p Y 2 и Y ₃ определяются формулами (20)–(22).

Характерной особенностью построенного решения является наличие рядов с экспоненциально убывающими во времени слагаемыми; другие составляющие решения, которые характеризуют процесс при t ^ м , представляют собой слагаемое с линейной зависимостью от времени и слагаемое с квадратичной зависимостью от координаты. Процесс диффузии или распространения тепла при наличии только этих двух слагаемых называют квазистационарным . Именно такие процессы характерны для установившихся режимов при нагревании и сушке плоских образцов [14; 20].

Приближенные формулы для переходов между слоями по времени

Обсудим теперь, каким образом на основе формул (20)–(22) может быть организована процедура расчета полей температуры и влагосодержания. В качестве первых шагов осуществим следующие преобразования.

Во-первых, воспользуемся разложением в ряд Фурье по косинусам на отрезке [0, d ]. Для функции y ( x ) оно имеет следующий вид [21]:

м

/ \        V-1        П n y (x )=у о+z yn cos dx;

n = 1

d у о=d J у (x)dx;

d yn=d J у (x)cos nnxdx.

Здесь y_n – коэффициенты Фурье.

Во-вторых, введем, как это принято в теории теплопроводности и в теории сушки, безразмерное время t* (переменную Фурье) формулой t * = atjd2.

В-третьих, примем в расчет, что, согласно сформулированной выше расчетной схеме, вычисления по формулам (20)–(22) следует производить не в любой момент времени t , а лишь в достаточно близкий к t = 0 момент t = A t , которому теперь будет соответствовать момент A t * = a A t J d ² .

Важно отметить, что на данном этапе мы можем сформулировать критерий близости к нулю момента A t *. Действительно, известно, что процессы диффузии выходят на квазистационарные режимы за время t * ~ 1 [14; 20], а это означает, что для наших расчетов следует взять A t * << 1.

Применив данные соображения к формулам (20)–(22), перепишем их следующим образом:

Y 1 ( x , A t * ) =

м

\ 2 , *          П n exp -(nn) At фn cos —x;

n = 1

d ²

Y 2 ( x ’ ^A t ) = "Г ^{f ) A} t ⁺

м

м

E ¹            2

—<1-exp -(nn) At d2

⁺    2

a n

*

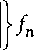
n n cos    x;

d

n = 1

n

Y 3 ( x , ^A t * ) =

^{d (} 2 Ц 1 +Ц 2 )

6      +Ц 1 ^x +

^(ц 2 ^ 1 ) x 2 +

+

d ( ^ 2 -Ц ₁ ) A t *

2 d     1 Г / у

+ -IZ-2 ^Ц 1 ^-Ц 2 ^{(- 1 )}

ⁿ n = 1 ^{n L}

X

x exp - ( n n ) 2 A t *

nn cos    x.

d

В этих формулах ф _n и f_n , n = 0,1, 2, „ - коэффициенты Фурье функций ф ( x ) и f ( x ) в разложениях по косинусам (23).

Получим теперь приближенный вид этих формул при нашем условии A t * << 1.

Рассмотрим сначала функцию Y1. Разложим в ряд экспоненту под знаком суммы и, выполняя двойное суммирование, станем выписывать получающиеся в результате этой операции слагаемые.

Сохранив среди них, кроме постоянного слага- емого фо, сначала члены, содержащие только At* и ф1, а затем члены, содержащие только At*, At *2, Ф1 и Ф2, будем иметь первое приближение Y1(1) и второе приближение Y^2) соответственно. Резуль- тат будет таким:

у ( 1 )

^Y 1

^-ф 0 + ( 1 ^-л 2

п

A t ) ф cos x ; d

„( 2 )           1                  1            1         л

Y 1 - Ф о +1 1 - л ² A t + п A t ² IФ 1 cos x +

(             2         )        d

+ ( 1 - 4 л ² A t * + 8 л ⁴ A t * 2 ) ф 2 cos ^ x .

Аналогичным образом можно построить и приближения более высоких порядков.

Применим точно такую же процедуру и по отношению к функции Y2. Разложив экспоненту в ряд и выполнив двойное суммирование, сохраним в полученном результате, кроме постоянного слага емого f0, сначала члены, содержащие только At* и f!, а затем члены, содержащие только At*, At *2, f1 и f2. Так мы получим первое приближение

( 1 ) Y ₂

Y ₂ :

и второе приближение

Y2(1)- — At * f0 + f cos—x ;(29)

² a I ^{JO J1} d Y

Y ₂

d ²

- A t *

a

\       1

f + 1 — n ² A t f cos — x +

0 I     2

+ —A t * ( 1 - 2 л ² A t * ) f2cos‘^ⁿx .

Как и выше, следуя указанному алгоритму, можно получить приближение любого порядка.

Наконец, обращаясь к функции Y ₃ и сохраняя в (26) первые два члена ряда и первые два члена в разложении экспоненты, получим первое приближение для этой функции:

⁽¹⁾ _ d ⁽ 2 P 1 +P 2 )

^Y 3 ^-       6      ⁺ H ^{x +}

⁺ d ( ^ 2 ^- P 1 ) ^A t * + — ( P 1 + ^ п ²

x 2 +

2 d

( 1 -n ² A t * )

п cos x +

d

2 d ( Ц} -^2 )                 2 л

—■*—¹--- ²¹ ( 1 - 4 n ² A t * ) cos — x .

_п ²    4                     d

Высшие приближения могут быть получены без затруднений.

Обсуждение результатов

В кратком виде созданный нами расчетный алгоритм выглядит следующим образом. Исходными являются начальные распределения температуры фт(x) и влагосодержания фи(x). Пользуясь ими, рассчитываем функцию fU(x), число μU и сформулируем задачу Неймана (10) для расчета поля влагосодержания U(x, t). Решив эту задачу (об этом будет сказано ниже), рассчитываем функ- цию fT(x), число μT и ставим задачу Неймана (11) для расчета поля температуры T(x, t). Она решается тем же способом, что и задача для поля влагосо-держания. Далее функции U(x, t) и T(x, t) рассчитываются в близкий к t = 0 момент t = At. Полученные функции координаты x объявляются начальными распределениями, после чего изложенный выше алгоритм перехода между соседними слоями по времени повторяется.

Напомним теперь алгоритм решения задач Неймана. Для определенности, будем говорить о задаче (10). Ее решение имеет вид

U - U 1 + U 2 + U 3 , где функции в правой части этого равенства могут быть найдены или по формулам (20)-(22) (аналитические решения, выраженные через исходные данные задачи), или по формулам (24)-(26) (аналитические решения, содержащие безразмерное время и коэффициенты Фурье от заданных функций), или по формулам (27)–(31) (приближенные формулы, которые и должны быть использованы в вычислительной программе). Во всех перечисленных формулах Y i , Y 2 , Y ₃ следует заменить на U 1 , U 2 , U ₃; ф ( x ), f ( x ), а , р₁ заменить на ф U ( x ), f U ( x ), a m , p U ; положить P 2 = 0. Схема решения задачи (11) выглядит аналогично.

По своей сути основная вычислительная работа при переходе на новый слой по времени заключается в расчете по формулам (23) коэффициентов Фурье ф n и f n от функций, определяемых распределениями температуры и влагосодержания на предыдущем слое по времени. Этим предлагаемая расчетная схема принципиально отличается от стандартных процедур сеточных методов, в которых указанные распределения входят в виде массивов в СЛАУ высоких порядков, которые и нужно решить, чтобы осуществить переход между слоями по времени [22]. Преимущества, которые открывает этот новый расчетный метод, могут быть предметом дальнейших исследований. Следует сравнить два метода по критерию сходимости, по объему расчетов, по удобству отладки, коррекции и переходу к другим исходным данным.

Еще одной важной особенностью нового алгоритма, отличающей его от сеточных алгоритмов, является тот факт, что исходные формулы (24)–(26), с помощью которых осуществляется переход между слоями по времени, имеют аналитический (формульный) вид. Конечно, при проведении расчетов мы используем их в приближенном виде (27)–(31), но само существование аналитических решений на малых участках между слоями по времени является принципиальным. Пользуясь ими, можно поставить задачу о нахождении асимптотики полей температуры и влагосодержания при t →∞, которые имеют большое значение для практики. Отметим здесь, что формулы (24)–(26) уже содержат характерные для асимптотических режимов линейную функцию по t и квадратичную функцию по x, и они описывают отклонение от этого режима. Впрочем, в случае пластины, как и в случае некоторых других областей с простой геометрией, асимптотические распределения авторами уже построены [15; 23–26]. Но, пользуясь новым алгоритмом и аппаратом функций Грина, способ построения асимптотических полей можно распространить и на области с произвольной геометрией.

По существу, основная идея статьи состоит в том, что в сеточных методах вся вычислительная работа производится «с нуля», в то же время при использовании функций Грина большая часть этой работы, которой учитываются свойства материала и геометрия области, оказывается уже проделанной, и она содержится в собственных числах и собственных функциях задачи Штурма – Лиувилля, в результате чего расчетный алгоритм может быть существенным образом упрощен. Эта идея в литературе по теории сушки пока еще не нашла должного применения.

Заключение

Сформулирована начально-краевая задача для расчета полей температуры и влагосодержания в плоском образце, обдуваемом воздушным потоком и находящемся под воздействием двух видов электромагнитных излучений, с большой и с малой по сравнению с толщиной образца глубиной проникновения. В отношении своих физических свойств материал пластины предполагается однородным, а в качестве математической модели распространения тепла и влаги сквозь пористую среду используются уравнения А.В. Лыкова. Краевые условия задачи являются нелинейными, что обусловлено учетом теплообмена излучением и принятием для интенсивности массообмена формулы испарения Дальтона.

Решение задачи проведено комбинацией численного метода с применением сетки по коорди- нате и по времени и аналитического метода, использующего разделение переменных, т. е. метода Фурье, который непосредственно к исходной задаче применен быть не может.

С помощью процедуры «расщепления» на малом временном интервале между двумя слоями по времени формулируются отдельные начальнокраевые задачи для полей температуры и влагосо-держания. Они имеют вид связанных условиями сопряжения задач Неймана для неоднородных уравнений параболического типа с неоднородными краевыми и начальными условиями. Общие решения этих задач имеют аналитический вид и строятся методом Фурье, для чего используется известная из литературы функция Грина задачи Неймана для однородной пластины, которая содержит собственные числа и собственные функции поставленной ей в соответствие краевой задачи Штурма – Лиувилля. Для перехода к новому слою по времени численными методами рассчитываются коэффициенты Фурье в разложении по косинусам от сеточных функций, определяемых распределениями температуры и влагосодержа-ния на предыдущем слое по времени, после чего эти коэффициенты подставляются в общие решения задач Неймана.

Предложенный расчетный алгоритм, использующий функции Грина, имеет принципиальное отличие от стандартных алгоритмов сеточных методов, в которых для перехода между слоями по времени требуется многократное решение систем линейных алгебраических уравнений высокого порядка. Сравнение двух методов расчета по различным критериям будет проведено авторами в ходе дальнейших исследований.

Наличие между слоями сетки аналитических решений с экспоненциально убывающими во времени слагаемыми позволяет ставить вопрос о применении нового алгоритма для расчета асимптотических распределений температуры и влаго-содержания, которые имеют важное значение для практики и могут быть использованы для наглядного представления основных закономерностей электромагнитной сушки и для расчета полей температуры и влагосодержания в первом приближении.

Исследование выполнено при финансовой поддержке РФФИ и Администрации Волгоградской области в рамках научного проекта № 19-48-340015 р_а.