Применение метода Фурье для решения задач теории сушки электромагнитным излучением

В литературе по математической физике разработано большое количество аналитических и численных алгоритмов решения начально-краевых задач для дифференциальных уравнений в частных производных гиперболического и параболического типов и краевых задач для уравнений эллиптического типа. Основная часть этих процедур, например различные варианты метода сеток, без труда переносится и на случай, когда задачи формулируются не для одного уравнения, а для систем связанных дифференциальных уравнений в частных производных для нескольких искомых функций. Однако в случае такого важного для практики метода, как метод разделения пере-

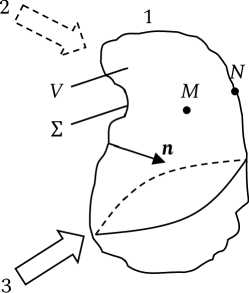
Рис. Схема электромагнитной сушки: 1 – влажный образец; 2 – воздушный поток; 3 – электромагнитная волна

менных ( метод Фурье ), этот перенос, за редкими исключениями, осуществлен быть не может. Причина в том, что из системы дифференциальных уравнений в частных производных, в отличие от системы обыкновенных дифференциальных уравнений, с помощью операций дифференцирования и исключения неизвестных в общем случае нельзя получить отдельные уравнения для каждой из искомых функций, к которым и мог бы быть применен хорошо разработанный в математической физике аппарат решения задач методом Фурье. Эта проблема обсуждается в [1]. Именно с такой проблемой мы и встречаемся при решении начальнокраевых задач теории сушки электромагнитным излучением, которые и являются предметом рассмотрения в настоящей работе.

Для решения указанной проблемы ниже будет впервые сформулирован и применен для решения задач теории сушки вычислительный алгоритм, который может быть назван «расщеплением процесса по физическим факторам». Идея расщепления, но в применении к задаче для одного дифференциального уравнения в частных производных (задача о распространении загрязняющей субстанции в окружающей среде) обсуждалась также в работе [2]. Отправляясь от этой идеи, здесь мы построим алгоритм, в рамках которого на следующих друг за другом и разделенных небольшими промежутками в ремени с лоях разностной сетки lm^^m © Афанасьев А.М. и др., 2019

будут последовательно решаться методом Фурье начально-краевые задачи для уравнения распространения тепла и уравнения распространения влаги. Мы обсудим преимущества нового расчетного метода, сравнив его с методами непосредственного численного решения исходной начально-краевой задачи, и рассмотрим применение построенного алгоритма для исследования асимптотических режимов электромагнитной сушки.

1. Математическая модель электромагнитной сушки

Принципиальная схема сушки показана на рисунке. Влажный образец обдувается воздушным потоком и подвергается воздействию электромагнитных волн. Образец состоит из двух компонентов: твердой основы (капиллярно-пористое тело) и воды. В качестве математической модели распространения тепла и влаги сквозь пористую среду будем использовать подход, принятый в те- ории тепломассопереноса А.В. Лыкова. Начальнокраевая задача для расчета функций T = T(M, t) и U = U(M, t) - распределений температуры и влаго-содержания в области V с границей S как функций переменной точки М и времени t – ставится следующим образом [3–5]:

с р д T д t = div ( k grad T ) + + rYрд U / д t + W ; M e V ; д Uy* д t = div ( a m grad U ) + + div ( a m 8 grad T ) ; M e V ;

Q ( N , t ) + r ( 1 -y ) J ( N , t ) =

= k д T д n ( N , t ) + S ( N , t ) ; N eS ;

J ( N , t ) = a _т рд U / д n ( N , t ) +

+ a _т р8д T /д n ( N , t ) ; N eS;

T ( M ,0 ) = T ⁰ ( M ) ;

U ( M ,0 ) = U ⁰ ( M ) ;

M e V + S ; t = 0.

Здесь с, р, k, y, am, 8 — теплофизические характеристики материала, а именно: удельная теплоемкость, плотность в сухом состоянии, коэффициент теплопроводности, критерий испарения, коэффициент диффузии влаги, относительный коэффициент термодиффузии влаги, которые считаются известными функциями переменной точки, а также температуры и влагосодержания в этой точке; r – удельная теплота парообразования воды; W = W(M, t) - плотность внутренних источников тепла, вызванных поглощением проникающего электромагнитного излучения; S = S(N, t) - плот- ность поверхностных источников тепла, вызванных поглощением излучения с малой глубиной проникновения; д/дn - символ производной по направлению внутренней нормали к границе S; T0(M) и U0 (M) – заданные функции, определяющие распределения температуры и влагосодер-жания в начальный момент времени t = 0; Q и J -интенсивности тепло- и массообмена поверхности образца с воздушной средой, которые в каждой точке поверхности N однозначно определяются температурой в этой точке Т и рассчитываются по формулам q (N, t )=оa [(T (N, t)+T )4—(TB+T )4 + a w [T (N, t)-TB ];

+

J ( ^N , t ) = « m [ P ( T ( ^N , t ) ) -Ф- P ( T B ) ] ;

P ( T ) = 6,03 ■ 10 ^{- 3} exp ^17,3 T .

T + T 2

В этих формулах: ст - постоянная Стефана-Больцмана; тА - коэффициент теплового излуче ния; TB и ф - температура и влажность воздуха за пределами пограничного слоя вблизи точки N; aw и am - коэффициенты тепло- и массообмена поверхности образца с воздушной средой; P(T) – функция, моделирующая зависимость относи- тельного парциального давления насыщенного водяного пара от его температуры Т при общем нормальном давлении; T1 = 273 °C и T2 = 238 °C -постоянные.

Система двух связанных уравнений параболического типа (1) и (2) моделирует процессы распространения тепла и влаги сквозь пористую среду в области V . Слагаемое с множителем д U /д t в правой части (1) есть плотность внутренних источников тепла, вызванных процессами испарения жидкости или конденсации пара. Краевые условия (3) и (4) имеют смысл баланса потоков тепла и влаги на поверхности S . Они не могут быть отнесены ни к одному из стандартных краевых условий математической физики (Дирихле, Неймана или третьего рода). Входящая в эти формулы интенсивность теплообмена Q , согласно (6), включает теплообмен конвекцией и теплообмен излучением; интенсивность массообмена J , согласно (7), принимается в виде закона испарения Дальтона.

Ниже мы будем считать, что на каждом шаге вычислений плотность внутренних источников тепла W и плотность поверхностных источников тепла S однозначно определяются текущими распределениями температуры Т и влагосодер-жания U . Алгоритм расчета функций W ( T , U ) и S ( T , U ) изложен в работах авторов [6; 7].

2. Алгоритм метода расщепления

Исследование сформулированной начальнокраевой задачи (1)-(7) будем вести следующим образом. Начиная с момента t = 0 и пользуясь заданным начальным распределением T ⁰( M ), мы сможем вычислить во всех точках области V вто-

рое слагаемое в правой части уравнения (2). Вводя для него обозначение

div ( a m 5 grad Т ⁰ ( M ) ) = H ⁰ ( M ) ,                   (8)

получим для поля влагосодержания U следующее уравнение параболического типа:

д U / д t ( M , t ) =

= div ( a _m grad U ( M , t ) ) + H ⁰ ( M ) .

но описывать поведение поля U ( M , t ) лишь вблизи начального момента t = 0. Получить из исходной системы (1)-(7) отдельную начально-краевую задачу для поля U ( M , t ), решение которой давало бы описание этого поля в любой момент времени, оказывается невозможным.

Процедура решения задачи (14) методом Фурье будет рассмотрена ниже. Используя найденную в результате этой процедуры функцию U ( M , t ), вычислим во всех точках М производную д U /д t ( M , 0) (как будет ясно из дальнейшего, эта операция может быть выполнена аналитически ). После этого, обозначив

Исходя из того же начального распределения температуры T ⁰ ( M ) и рассматривая его в точках границы S , т. е. оперируя функцией Т ⁰( N ), мы сможем найти с помощью (6) и (7) интенсивности тепло- и массообмена на поверхности образца в рассматриваемый начальный момент t = 0:

r урд U / д t ( M ,0 ) + W ( M ,0 ) = F ⁰ ( M ) (15) (эта функция имеет смысл плотности внутренних источников тепла), получим с учетом (1), (5) и (12) для нахождения поля температуры Т ( M , t ) задачу Неймана, аналогичную той, которая приведена была выше для поля влагосодержания:

Q ( N ,0 ) = о A

( ^{Т 0} ( ^N ) + ^Т 1 ) ⁴ - ( ^Т в + ^Т 1 ) ⁴

+ « w [ ^{Т 0} ( ^N ) - T _B ]- Q ⁰ ( ^N ) ;

+

с р д Т /д t ( M , t ) = div ( к grad Т ( M , t ) ) +

+ F ⁰ ( M ) ; M e V ;

д Т /д n ( N ) = ^ ⁰ ( N ) ; N eS ;

Т ( M ,0 ) = Т ⁰ ( M ) ; t = 0.

J ( N ,0 ) = a m [ P ( Т ⁰( N ) ) -ф P ( T _B ) ] = J ⁰ ( N ) .       (11)

После этого из краевых условий (3) и (4) могут быть

определены нормальные производные полей Т и

U на границе S в тот же самый момент t = 0:

д Т / д n ( N ,0 ) = ^[ Q ⁰ ( N ) +

+ r ( 1 -у ) J ⁰ ( N ) - S ( N ,0 ) ] /к ^⁰ ( N ) ;

д U / д n ( N ,0 ) = J ⁰ ( N )/( a m p ) --5^ 0 ( N ) = ц ⁰ ( N ) .

Возвращаясь к полю влагосодержания U ( M , t ) и рассматривая его вблизи момента t = 0, пренебрежем изменением во времени нормальных производных д Т /д n и д U /д n . Тогда с учетом (5), (9) и (13) для нахождения этого поля получим следующую начально-краевую задачу:

д и /д t ( M , t ) = div ( a _m grad U ( M , t ) ) +

+ H ⁰ ( M ) ; M e V ;

д U /д n ( N ) = Ц 0 ( N ) ; N eS ;

U ( M ,0 ) = U ⁰ ( M ) ; t = 0.

Как и в случае с задачей (14), решение задачи (16) будет давать приближенное описание поля T ( M , t ) лишь вблизи момента t = 0. Решив эту задачу методом Фурье, найдем температуру как функцию координат и времени.

Таким образом, нами построены распределения U ( M , t ) и T ( M , t ). Ограничив их справедливость малым интервалом времени 0 <  t <А t , вычислим функции координат U ( M , А t ) и Т ( M , А t ). Объявив их начальными распределениями и повторив изложенный выше алгоритм расчетов, мы найдем новые функции координат U ( M , 2 А t ) и Т ( M , 2 А t ) в момент t = 2 А t и т. д., вплоть до некоторого заданного момента окончания расчетов, чем и будет завершена процедура построения решения сформулированной задачи.

Важно отметить, что здесь мы построили процедуру «развязывания» общей начально-краевой задачи (1)-(7) для двух функций Т и U , непосредственное исследование которой методом Фурье произведено быть не может, на две отдельные задачи для этих функций, задачи (14) и (16), к которым метод Фурье уже вполне может быть применен.

Это задача Неймана для неоднородного уравнения параболического типа с неоднородными краевыми и начальными условиями . Подчеркнем, что по построению решение этой задачи будет приближен-

3. Решение задачи Неймана (16)

Остановимся теперь на способе решения задач Неймана (14) и (16). Для определенности далее

будем говорить о задаче (16) для поля температуры T(M, t). Задача (14) для поля влагосодержания U(M, t) может быть исследована аналогичным об- разом.

Как известно [8-10], в рамках метода Фурье решение начально-краевой задачи (16) может быть найдено в замкнутом виде (в квадратурах), т. е. записано в виде интегралов от некоторых известных функций, если предварительно построена функция Грина G ( M , t , M ') этой задачи:

V n ( ^M ) V n ( ^M ‘ )

G ( M , t , M ' ) = £ exp ( -X n t )

n = 1

Здесь X _n и v n ( M ) - собственные числа и собственные функции задачи Штурма – Лиувилля :

div (k grad v) + Xpv = 0, M e V, dv]dn (N ) = 0, N eZ, отвечающей решаемой задаче (16). В первом уравнении использовано обозначение p(M ) = = c(M)p(M), а символом ||vn|| в формуле (17) обозначен квадрат нормы собственной функции:

II v n |F = JJJ v n ( ^M ) Р ( ^M ) ^dV .                        (19)

V

Заметим, что для областей произвольного вида нахождение собственных функций в явной аналитической форме сопряжено с большими трудностями и чаще всего может быть выполнено только приближенно: сеточными методами, сведением задачи к интегральному уравнению или с использованием пакетов прикладных программ. Для ряда областей с простой геометрией собственные функции могут быть выписаны явно, хотя это и требует введения специальных функций [8–10].

Как было сказано при постановке задачи, теплофизические характеристики материала k , c , р , a m , 5 , у считаются заданными функциями переменной точки, а также температуры и влагосодер-жания в этой точке. Например, коэффициент теплопроводности является функцией вида k = k [ M , T ( M , t ) , U ( M , t ) ]

(явная зависимость от координат и неявная зависимость от координат и от времени). При таком подходе мы будем вынуждены на каждом слое по времени t = 0, At, 2Аt и т. д. заново решать задачу штурма – Лиувилля (18), причем раздельно для полей Т и U, что потребует больших вычислительных затрат. Если же при моделировании характеристик среды учитывать лишь явную зависимость от координат (стационарная неоднородная среда), т. е., например, в случае с коэффициентом теплопроводности ограничиться зависимостью вида k = k(M), то задачу Штурма - Лиувилля достаточно будет решить только один раз, но все-таки опять раздельно для поля температуры и поля вла-госодержания. Если же среда однородная, то задача штурма – Лиувилля решается один раз, и для обоих полей она оказывается одинаковой.

Допустим, что задача штурма – Лиувилля (18) решена, т. е. множества { X _n } и { v n ( M )} построены. Тогда построена и функция Грина (17), и значит, как говорилось выше, решение задачи Неймана (16) может быть записано в квадратурах. Это решение представляется в виде суммы

T ( M , t ) = T 1 (M , t ) + T ₂( M , t ) + T 3 ( M , t ),               (20)

где функциями T 1 ( M , t ), T ₂( M , t ) и Т з ( M , t ) учитываются вклады в общее решение соответственно начальным условиям T ⁰( M ), плотности внутренних источников тепла F ⁰ ( M ) и краевых условий £ ° ( N ). Указанные слагаемые формулы (20) имеют следующий вид [9]:

T1 (M, t) = JJJ G (M, t, M') p (M') T0 (M') dV';(21)

V t

T2 (M, t) = J JJJ G (M, t - t, M') F0 (M') dV'dt;(22)

0 V

T 3 ( M , t ) =

= T (M)- JJJ G (M, t, M') p (M') T (M') dV ‘ +

V

t

+ f 0 J JJJ G ( M , t — t , M ') dV d t .

0 V

В последней формуле постоянная f0 дается выражением f 0 = VV ^J k ^0 (N) d^                           (24)

z где V - объем области V, а поле T(M) находится как решение задачи Неймана для уравнения Пуассона:

^div ( k grad T ( M ) ) = f ⁰; M e V ;

”d T /d n ( N ) = ^ ⁰ ( N ) ; N eZ ;                     ⁽²⁵⁾

T ( p ) = 0.

Здесь Р – произвольная фиксированная точка в области построения решения.

Мы рассмотрели решение задачи (16) для поля температуры Т . Задача (14) для поля влагосодер-жания U решается аналогично.

4. Сравнительная характеристика решения задач сушки сеточными методами и методом Фурье

При использовании сеточных методов аппроксимация исходных уравнений (1)–(7) конечными разностями производится на базе сетки с некоторыми шагами по координатам А х , A y , A z и по времени A t . Вводятся также сеточные функции T _i ⁿ _jk , U _i ⁿ _jk , S _i ⁿ _jk , W _i ⁿ _jk (нижние индексы обозначают номера узлов сетки по координатам, а верхний индекс – номер слоя по времени), отвечающие искомым распределениям температуры, влагосодер-жания и плотности поверхностных и внутренних источников тепла. На каждом новом слое по времени каждая из четырех искомых сеточных функций находится как решение соответствующей ей одной из четырех систем линейных алгебраических уравнений (СЛАУ). При этом, например, в СЛАУ для нахождения T _i ⁿ _jk будут входить значения этой функции на новом слое и на предыдущих слоях по времени, а функции U _i ⁿ _jk , S _i ⁿ _jk , W _i ⁿ _jk будут браться большей частью с предыдущих слоев, за исключением тех функций, значения которых на новом слое к этому моменту уже определены. Такая процедура требует больших вычислительных затрат. Реализация этого алгоритма для решения пространственно одномерных и пространственно двумерных задач электромагнитной сушки осуществлена авторами соответственно в [11; 12] и [13; 14]. Двумерные задачи рассматривались в рамках метода переменных направлений [15].

Проведем сравнение алгоритмов перехода между соседними слоями по времени в методе сеток и методе Фурье. В методе сеток для этого нужно несколько раз решить СЛАУ высокого порядка. В методе Фурье дело обстоит иначе. Благодаря процедуре расщепления исходной задачи (1)–(7) мы имеем отдельные задачи для поля влагосодер-жания и поля температуры, задачи (14) и (16) соответственно. Эти задачи решаются одинаково, поэтому достаточно будет проанализировать решение только одной из них, например задачи (16). Ее решение, согласно (20), получается наложением полей T ₁, T ₂ и T ₃, которые, в свою очередь, находятся из (21)–(23) с помощью операций интегрирования. Но интегралы в (23) имеют такую же структуру, как и в предыдущих двух формулах, поэтому нам достаточно будет проанализировать лишь вычисления по формулам (21) и (22). В этих формулах T 0 ( M ') и F 0 ( M ') - распределения температуры и плотности внутренних источников тепла на пре-

дыдущем слое по времени t = 0. Значит, чтобы найти Т ₁ и Т ₂ в следующий за моментом t = 0 момент t = A t , мы должны проделать следующие вычисления:

T 1 ( M , A t ) = |Л G ( M , A t , M ' ) p ( M ' ) T 0 ( M ' ) dV ';

V

T 2 ( M , A t ) =

( A t

= Ш J G (M

V <  0

, A t - t ,

)

M ' ) d t

J

F ⁰ ( M ' ) dV '.

Если в достаточно общем случае среда стационарная неоднородная, то, как уже говорилось, задача штурма – Лиувилля решается не на каждом слое по времени, а только один раз, но отдельно для полей Т и U . Таким образом, функция G ( M , A t , M ') в первом интеграле и интеграл по времени во втором интеграле могут быть вычислены раз и навсегда, и переход между слоями по времени будет сводиться просто к вычислениям объемных интегралов. Благодаря этому обстоятельству сокращается объем расчетов, а сама процедура становится удобной для отладки, коррекции и перехода к другим исходным данным.

В действительности при переходе между соседними слоями по времени, кроме вычисления объемных интегралов, нужно будет еще каждый раз решать численными методами задачу (25) для вспомогательной функции T ( M ), входящей в решение (23) для T ₃ ( M , t ). Как и в случае с задачей штурма – Лиувилля (18), она может быть решена сеточными методами, методом интегральных уравнений или с помощью пакетов прикладных программ. Принципиальное значение имеет тот факт, что эта частная краевая задача является существенно более простой по сравнению с исходной начально-краевой задачей (1)–(7).

5. Переход к асимптотике по времени

При исследовании процесса сушки сеточными методами на идущих друг за другом слоях разностной сетки по времени последовательно выводятся распределения температуры, влагосодер-жания и другие данные, что позволяет детально проследить за развитием процесса в различных ситуациях. Однако по совокупности численных экспериментов, выполненных при различных входных данных, часто оказывается невозможным выявить общие закономерности сушки, что затрудняет и общий ее анализ, и производство инженерных оценок для организации режимов с

наперед заданными свойствами. В связи с этим важное значение приобретает следующее обстоятельство. Как известно, сушка влажных материалов большей частью происходит так, что после непродолжительного начального периода , когда наблюдаются переходные процессы , а влагосодер-жание материала почти не изменяется, наступает протяженный во времени и имеющий основное значение для практики установившийся период ( период постоянной скорости сушки ), когда и происходит удаление основной части влаги. Математическое описание этого периода является намного более простым, чем исходное описание. Поле температуры оказывается близким к стационарному однородному (слабо изменяется и во времени, и в пространстве), такие же свойства приобретает и поле скорости сушки (поле производной от влагосодержания по времени). Формально эти решения получаются из построенного выше решения Фурье как асимптотические (для больших моментов времени), что позволяет ограничиться несколькими первыми членами разложения в рядах, которыми такие решения представляются. Поведение полей температуры и влагосодержания во времени в таких решениях будут определяться первыми собственными числами задачи штурма – Лиувилля, распределения этих полей в пространстве – первыми собственными функциями этой задачи, а переходные процессы будут полностью исключены. Такие решения позволят в наглядном виде представить общие закономерности сушки. Они могут быть использованы на практике для инженерных оценок и давать характеристики сушки в первом приближении.

Рассмотрим пример. Обратимся к решению (22) для поля температуры T ₂ ( M , t ). Подставим на место функции Грина G выражение (17) и ограничимся первым членом ряда для этой функции (это можно будет сделать для больших моментов времени: как известно, собственные числа X _n задачи штурма – Лиувилля (18) являются положительными и быстро возрастают с ростом номера n [8]). Тогда температурное поле примет следующий вид:

t

T 2 ( M , t ) * J JJJ exP [^-X 1 ( t ^{- т} ) ] ^x

0V x v 1(M) v 1 (M ) f0 (m,) dvdт = v1

= v 1 ( M )

v 1 ²

JJJ v 1 ( M ■ ) F 0 ( M ■ ) dV'

V

t

x J exp [-X1 (t - т)] dт = v 1 (M)

v 1 ²

JJJ v 1 ( M ■ ) F 0 ( M ) dV ■ l-ex^ .

Назовем величину

F = fJf v 1 ( M ■ ) F 0 ( M ') dv'                        (28)

V обобщающим воздействием на образец, порожден- ным внутренними источниками с распределением F0 (M) и отвечающим собственной функции v1(M). Тогда полученную выше формулу можно будет переписать так:

T 2 ( M , t ) *

^v 1 ( ^M ) _D1 ^{- ex}P ( ^-X 1 t ) ^F

II v ,12              ^X >

Если мы сможем на основании тех или иных разумных предположений указать распределение источников F ⁰( M ) по объему образца, то постоянная F может быть вычислена, а значит, будет вычислена и реакция (отклик) температурного поля Т в каждой точке образца М на это воздействие при больших моментах времени. В частности, мы видим, что при t ^ » этим откликом будет стационарное поле.

ясно, что получение таких аналитических решений, позволяющих приближенно рассчитывать параметры процесса и получать представление о его основных закономерностях в асимптотических режимах, имеет большое значение для практики. Разумеется, приведенный здесь анализ нельзя напрямую распространить на процессы, происходящие при сушке электромагнитным излучением. Ведь рассуждение велось всего лишь для одного из трех слагаемых поля температуры, которое, в добавление к этому, может считаться справедливым лишь вблизи выделенного слоя по времени. Исследовать возможность распространения сделанных выводов на всю сушку и определить границы их применимости – одна из задач дальнейших исследований в этом направлении.

Получение асимптотических решений задач электромагнитной сушки, которое возможно при использовании метода функций Грина и о котором говорилось выше, мы рассматриваем как развитие подходов, уже применявшихся авторами в рамках работ над региональными проектами РФФИ (2004–2018 гг.), в ходе которых были впервые получены предназначенные для инженерных оценок асимптотические распределения темпера- туры и влагосодержания при электромагнитной сушке однородных тел простой формы. Именно в качестве областей построения были рассмотрены пластина [4; 16], цилиндр [17], шар [18], прямоугольник [19] и параллелепипед [20]. Все найденные решения в качестве характерных особенностей имеют стационарное температурное поле (дTдt = 0) и квазистационарное поле влагосодержания (дUjдt = const). В рамках настоящего исследования мы намерены получить обобщение решений такого рода для тел с более сложной геометрией и для режимов из более широкого класса. Аналитические решения, о которых было сказано выше, могут быть использованы для тестирования новых вычислительных программ.

Заключение

Сформулирована начально-краевая задача для расчета полей температуры и влагосодержания в неоднородном теле произвольной формы, обдуваемом воздушным потоком и находящемся под воздействием электромагнитного излучения с заданными характеристиками. Проведена процедура «расщепления процесса по физическим факторам», с помощью которой осуществлен переход от исходной начально-краевой задачи для двух искомых функций, температуры Т и влагосодер-жания U, непосредственное исследование которой методом Фурье произведено быть не может, на последовательность отдельных задач для этих функций, имеющих вид задач Неймана для неоднородных уравнений параболического типа с неоднородными краевыми и начальными условиями, к которым классический метод Фурье уже вполне может быть применен. Эти отдельные задачи сопоставляются узлам сетки по времени, и их решения приближенно описывают поведение полей температуры и влагосодержания вблизи этих узлов. Сами решения записываются в общем виде, а затем они уточняются таким образом, чтобы при переходах между соседними слоями выполнялись условия сопряжения. Эти общие решения строятся методом Фурье, для чего предварительно для каждой задачи определяется ее функция Грина, которая формируется с помощью собственных чисел и собственных функций поставленной ей в соответствие краевой задачи штурма – Лиувилля. В достаточно общем случае, когда среда является стационарной неоднородной, функция Грина оказывается одной и той же для всех слоев по времени, но отдельной для поля температуры и поля влагосодержания. Время входит в функцию Грина в формульном виде, и это обстоятельство сокращает объем необходимых вычислений, делает алгоритм расчета прозрачным, удобным для коррекции и отладки. В этом новом алгоритме переход между соседними слоями по времени сводится к решению существенно более простой, по сравнению с исходной начально-краевой задачей, задаче Неймана для вспомогательной функции координат и к вычислению объемных интегралов от функций, рассчитанных на предыдущем слое, что выгодно отличает метод Фурье от сеточных методов, где для такого перехода требуется многократное решение систем линейных алгебраических уравнений высокого порядка.

Кроме того, в рамках нового расчетного алгоритма появляется возможность исследовать имеющие основное значение для целого ряда приложений установившиеся режимы сушки (режимы постоянной скорости), которые следуют за переходными режимами и математическое описание которых является существенно более простым, чем исходное описание. Формально эти решения получаются из решения Фурье как асимптотические (для больших моментов времени), что позволяет ограничиться несколькими первыми членами разложений, которыми такие решения представляются. Поведение полей температуры и влагосодержания во времени в таких решениях определяются первыми собственными числами задачи штурма – Лиувилля, а распределения этих полей в пространстве – первыми собственными функциями этой задачи. Решения из этого нового класса (асимптотические решения) могут быть использованы на практике для инженерных оценок и давать характеристики процесса сушки в первом приближении.

Исследование выполнено при финансовой поддержке РФФИ и Администрации Волгоградской области в рамках научного проекта № 19-48-340015 р_а.

Расшифровка индексов в – воздух;

m (англ. moisture) – влага;

w (англ. warmth) – тепло.