Применение метода Галеркина с разрывными базисными функциями к исследованию динамики изменения температуры и давления в пласте с нагнетательной скважиной и трещиной гидроразрыва

В настоящее время в связи с вводом в эксплуатацию месторождений с трудноизвлекаемыми запасами и значительной выработкой многих крупных месторождений развитие нефтегазовой промышленности России происходит на фоне внушительного падения запасов нефти и газа. Одним из важнейших факторов, оказывающих влияние на извлечение нефти из месторождения, является состояние призабойной зоны пласта (ПЗП). Важным источником информации о ПЗП являются гидродинамические исследования пластов и скважин (ГДИС).

В устоявшихся методах ГДИС анализируются кривые давления в бесконечном пласте при неустановившемся режиме радиальной фильтрации. Основные подходы (анализ данных по кривой падения давления и по кривой восстановления давления) базируются на решении уравнения пьезопроводности. Однако для более полного исследования скважин очень важно рассматривать, наряду с методами ГДИС, методы термометрии1. Для скважин с гидравлическим разрывом пласта такие исследования особенно важны. Отсюда возникает необходимость в разработке математической модели для системы «скважина – трещина – пласт»2. Использование методов термометрии скважин и пластов на сегодняшний день позволяет увеличить нефтеотдачу пластов за счет более эффективных мер по увеличению нефтедобычи.

Обзор литературы

Настоящая работа посвящена математическому моделированию процесса изменения температурного поля и поля давления в пласте с трещиной гидроразрыва под действием нагнетания охлаждающей жидкости в вертикальную скважину [1]. Для описания математической модели данного процесса используются уравнения конвекции-диффузии. В настоящее время существует множество подходов к решению этих уравнений. Одним из перспективных и активно развивающихся является метод Галеркина с разрывными базисными функциями [2–4], который прекрасно зарекомендовал себя для решения уравнений конвективного типа [5–8]. Также активно развиваются подходы к созданию лимитеров повышенного порядка точности, которые обеспечивают монотонность решения, полученного с помощью разрывного метода Галеркина [9–11]. Дальнейшее развитие метода Галеркина с разрывными базисными функциями привело к его модификации с использованием разнесенных сеток (Staggered Discontinuous Galerkin Method), которая объединяет хорошие качества этих способов [12–15]. К примеру, в ряде работ был построен оригинальный вычисли- тельный алгоритм, в котором вспомогательные переменные, введенные для понижения порядка исходных уравнений переноса тепла, рассчитываются на двойственной сетке, представленной в виде медианных контрольных объемов вокруг узлов основной сетки [16–19]. Искомые величины аппроксимируются на основной неструктурированной треугольной сетке.

Материалы и методы

Для описания динамики изменения температуры, скорости и давления будем рассматривать следующие уравнения, которые подробно представлены в одной из наших работ3.

Процесс переноса тепла:

a t  a La t ) a La t )

cp— =—I X— 1 + — I X— a t   ax ^ ax) ay ( ay)

( a t   a t )

- cp\ u --+ v —

[   ax     ay.

( x , y ) e D ,

max ,

T ( X , y ,0 ) 7 0 ,0 <  t <  T _max,

-X — - 0, ( x , y ) ed D ,0 <  t <  T _max, a n

-X— = p (T-Tr)nx + p (T-Tr)Пу,

p ( x,y ,0 ) = p о ( x,y ) ,0 <  t <  T _max,

- - I P = 0, ( X , y ) e8 D ,0 <  t <  T max , ц 8 n

P = P Г , ( x , У ) бГ ,0 <  t <  T max .

Для описания скорости течения жидкости используется закон Дарси4:

u = - — grad ( p ) , ( x , y ) e D .    (3)

Ц

Ранее авторами был представлен подробный вывод уравнений для решения систем (1)–(3) на неструктурированной двойственной сетке, здесь приведем лишь полученные выражения5.

Для решения системы (1) используются выражения:

cP T. 2o dT j J" к ^ i ^ k ^{dS =} “fc

■■ i—0 dt   к j                 ^к j n to Ljdl -xxk

-d) n, to ^ф^сЯ +   to^^dS + to^^dS - aKj y yYk       Kj x 0x        Kj y 0y

—

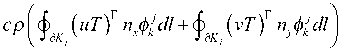
^a ( ^иф\к₊^ т^ефгф\Л

, ^T j ax ^{dS +} J K j T 0y ^dS ,

J K j V

V ф к ( x,y ) , k — 0...2,            ( 4 )

( ^X , У )^{еГ ,}0 <  t ^ T max .

Процесс изменения давления [20]:

c — - div — grad (p) = 0, r dt      (цJ

(x, y )e D,0 < t < T^(2)

S "^xLj J D^lvid =

5Dj                  Dj v vKx, y), k = ° —2,

Е М f „—d =

= - n X Tр/ j dl + T X ⁵^ dS , ⁵ d - y ^k         D -     g y

V i / k ( x , y ), k = 0...2.         (6)

Для решения систем (2), (3) используются выражения:

c r Е Е dp j f У n d = 1 K j n x u^ ⁺

+ n v ^jdl -   u ^k^SS -   v ("k>i dS, aK y Vk      k, 8x        k, 8y

• Vyk(x,y), k = 0_2,

E ^u i K v i v k dS =

• = - n ^— p ^T9^J_kdl +   p ^— ^^dS ,

• к , x p ^k       K j p 8 x

• Vфк(x,y), k = 0...2,(8)

E E v ' J к V i v k dS =

= ^_K n y - p ^Г j ⁺ J _K p - ^^dS , ⁸ K    ^           K , p 8 y

^^j{ x, y), k = 0^2, где ^i (x, y )}, {^/ (x, y )}

– системы

базисных функций, заданные на элементе Kj (элементы основной треугольной сетки) и Dj (элементы двойственной сетки) соответственно, в виде проекции на которые находятся температура, давление и компоненты вектора скорости6.

Для нахождения величин ( uT )^Г и ( vT )^Г на границах элементов в системе (4) используется потоковая функция

Лакса – Фридрихса⁷. При вычислении потоковых величин T ^г , ® f , ® y на границе элементов в системах (4)-(6) применяется потоковая функция [21]. С учетом использования двойственных сеток потоковые величины представляются в виде:

Т ^Г = Т ,

® Г = ® х - с _п ( T ⁺- T -) П х ,

^y= toy - С11 (T+-T-)Пу, где T+ - значение температуры из ячейки, для которой нормаль n = (nx, n ) является внешней, а T+ - значение температуры из ячейки, для которой нормаль n = (nx, ny) является внутренней; C11 – стабилизирующая добавка.

На граничных ребрах, с учетом типа граничного условия, получаем:

T - T+, юг = Р (T - Tr) nx,

^_у= р ( T - Т _г) П у .

Для вычисления потоковых величин p ^Г, u ^Г, v ^Г в системах (7)–(9) также используются стабилизирующие добавки, но в данном случае аппроксимация строится только на треугольной сетке. Вид потоковых функций представлен ниже:

_г_( ^{p +} + p ")

p "     2,

(и++u )         ,.

u ^г = —2-- ^с н ( p ⁺- Р ") n x ,

(v ++v ), v =    2—- - cii (p+- p") ny, где верхний индекс «+» обозначает величины из ячейки, для которой нормаль n = (nx, ny) является внешней, а верхний индекс «–» – величины из ячейки, для которой нормаль n = (nx, ny) является внутренней; C11 – стабилизирующая добавка.

На граничных ребрах получаем следующий вид:

pг = p+, г u = qnx, г

• V - qny.

В системах (4)–(9) необходимо с высокой точностью вычислять поверхностные и контурные интегралы. Для этого используются квадратурные формулы Гаусса [22]. Поверхностные интегралы вычисляются по трем точкам, контурные интегралы вычисляются с использованием двухточечного шаблона. Для подавления нефизических осцилляций используется лимитер TVD8. Для аппроксимации по времени используется явная схема Эйлера.

Результаты исследования

Описанный вычислительный алгоритм был реализован в виде программного пакета для расчета динамики изменения температуры и давления в нефтеносном пласте. Для сокращения времени расчетов была использована технология параллельных вычислений MPI.

Том 31, № 1. 2021

Для анализа полученных результатов рассматривалась следующая постановка задачи: T ₀ = 363 K, c = 2 000 Дж/кг·К, ρ = = 950 кг/м³, λ = 2,5208, µ = 0,315 ∙ 10^–4 Па∙с, p ₀ = 2,5 ∙ 10⁷ Па, p _Г = 2,5 ∙ 10⁷ Па, β = = 150 Вт/м²·K. Для трещины были заданы следующие значения параметров: c_r = = 4,18968 ∙ 10^–9 Па^–1, κ = 2,96 ∙ 10^–15 м². Для пласта были заданы следующие значения параметров: c_r = 0,2505 ∙ 10^–9 Па^–1, κ = 5 ∙ 10^–17 м².

Рассматривается область длиной 60 м и шириной 10 м. В центре области находится скважина с радиусом 0,025 м. Слева и справа к скважине симметрично примыкают трещины длиной 8 м и шириной 0,005 м каждая.

На рисунке 1 представлена расчетная сетка для описанной задачи. Вдоль трещины наблюдается заметное сгущение сетки. Расчетная сетка содержит 36 339 ячеек основной неструктурированной сетки.

Расчет производился с использованием параллельного комплекса программ на 12 процессорах [23]. На рисунке 2 представлена декомпозиция расчетной области по процессорам.

На практике наибольший интерес представляет состояние призабойной зоны пласта. В связи с этим, а также из-за большого масштаба задачи дальнейшие рисунки представляют не всю расчетную область, а ее часть, приближенную к скважине. На рисунке 3

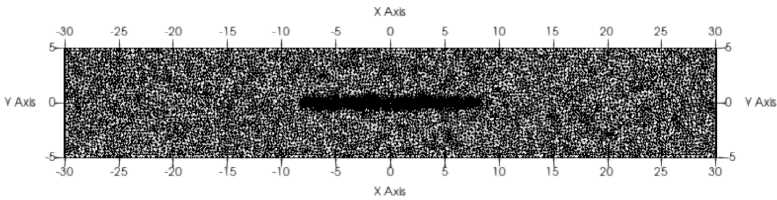
Р и с. 1. Сетка

F i g. 1. Mesh

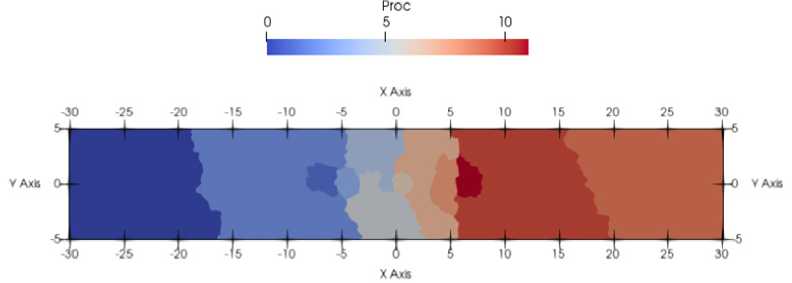
Р и с. 2. Декомпозиция расчетной области

F i g. 2. Decomposition of the computational domain

представлена расчетная сетка возле скважины, диаметр скважины 0,05 м.

На рисунках 4–6 представлено распределение поля давления в различные моменты времени. Из рисунков видно, что с течением времени вдоль трещины давление растет заметно быстрее, по сравнению с пластом, что согласуется с заданными параметрами задачи.

На рисунках 7–9 представлены картины распределения поля температуры в различные моменты времени. Из рисунков видно, что холодная закачиваемая через вертикальную нагнетательную скважину жидкость охлаждает пласт. Можно отметить, что вдоль трещины охлаждение происходит немного интенсивнее, что согласуется с наблюдаемой картиной распределения давления. Существенное уменьшение температуры наблюдаются вблизи скважины и вдоль трещины, в частности на ее створках.

Р и с. 3. Сетка возле скважины

F i g. 3. Mesh near the well

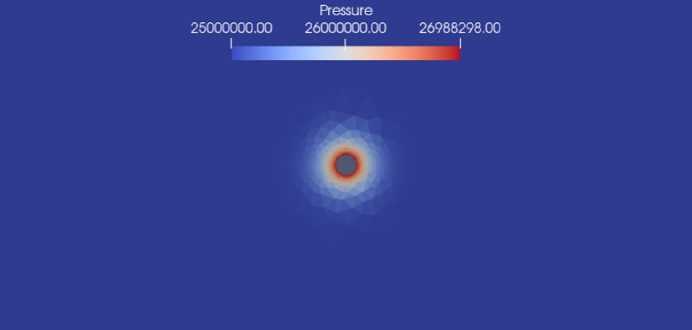
Р и с. 4. Распределение давления, t = 1 с

F i g. 4. Distribution of the pressure, t = 1 s

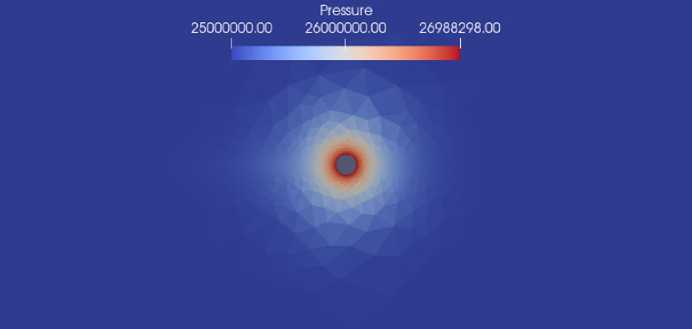
Р и с. 5. Распределение давления, t = 5 с

F i g. 5. Distribution of the pressure, t = 5 s

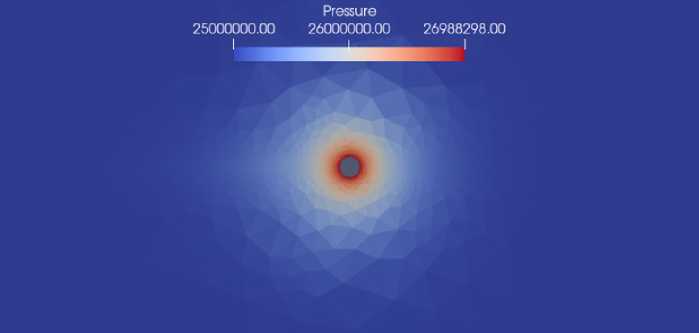
Р и с. 6. Распределение давления, t = 10 с

F i g. 6. Distribution of the pressure, t = 10 s

168                                                       Физико-математические науки

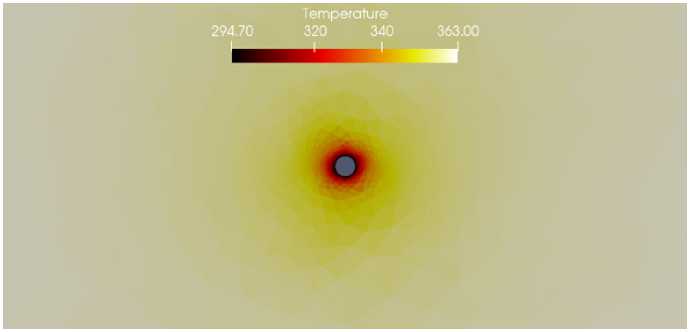
Р и с. 7. Распределение температуры, t = 1 с

F i g. 7. Distribution of the temperature, t = 1 s

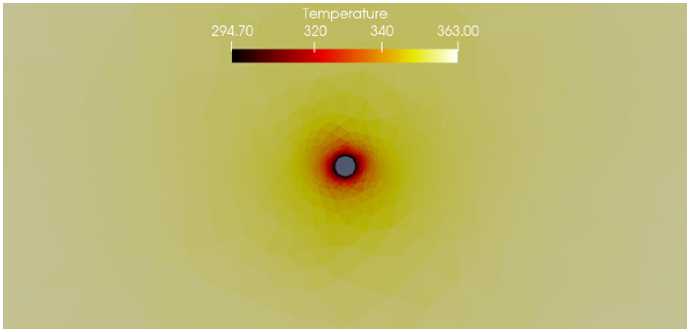
Р и с. 8. Распределение температуры, t = 5 с

F i g. 8. Distribution of the temperature, t = 5 s

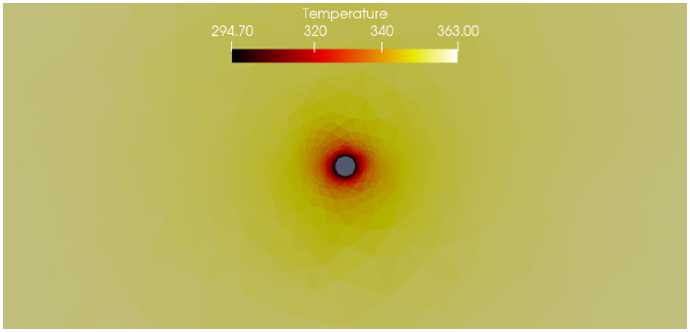
Р и с. 9. Распределение температуры, t = 10 с

F i g. 9. Distribution of the temperature, t = 10 s

Обсуждение и заключение

В настоящей статье разработан и реализован вычислительный алгоритм для моделирования динамики изменения температуры и давления в нефтеносном пласте. Алгоритм построен на основе метода Галеркина с разрывными базисными функциями на разнесенных неструктурированных сетках с применением технологии параллельных вычислений MPI. С использованием разработанного программного кода была исследована задача закачивания

Том 31, № 1. 2021

в пласт охлаждающей жидкости через вертикальную нагнетательную скважину. Можно сделать вывод, что результаты моделирования показывают адекватные картины для температурного поля и поля давления в пласте, соответствующие заданным начальнокраевым условиям. Для более точного моделирования рассматриваемого процесса в дальнейшем планируется решать данную задачу в трехмерной постановке на неструктурированных тетраэдральных сетках.

Поступила 09.10.2020; одобрена после рецензирования 10.12.2020; принята к публикации 20.12.2020

Благодарности: авторы выражают признательность анонимным рецензентам.

Все авторы прочитали и одобрили окончательный вариант рукописи.

172                                                       Физико-математические науки

Submitted 09.10.2020; approved after reviewing 10.12.2020; accepted for publication 20.12.2020

Acknowlegments: The authors express gratitude to the anonymous reviewers.

All authors have read and approved the final manuscript.

Физико-математические науки