Применение метода конечных элементов к расчету больших перемещений плоской линейно-упругой конструкции

Сов^еменная механика сплошной с^еды отличается большим ^азнооб^азием подходов к ^е-шению задачи о ^асчете больших пе^емещений конст^укций, ^азнооб^азен также и используемый тензо^ный а^сенал. Для описания нап^яженного состояния мате^иала наиболее ши^око используется тензо^ нап^яжений Коши [1–3], наследуемый п^актически без изменения из геомет-^ически линейного подхода, а также тензо^ы Пиолы–Ки^хгофа пе^вого и вто^ого ^ода [2, 3]. Еще большее количество тензо^ов описывает дефо^ми^ованное состояние мате^иала, нап^име^ [1–5]. Сюда относятся тензо^ы конечных дефо^маций Коши–Г^ина, Г^ина–Лаг^анжа, Альманси и д^. К^оме того в лите^ату^е, а также в некото^ых пакетах вычислительных п^ог^амм (в частности, в пакете ANSYS), для ^асчета конечных дефо^маций используют тензо^ лога^ифмической дефо^мации (тензо^ Генки) [5, 6], что делается, как показано в ^аботе [7], не всегда ко^^ектно. Подобное обилие ме^ нап^яжений и дефо^маций существенно усложняет ^ешение, п^ичем даже для линейно-уп^угих конст^укций. Поэтому целью данной ^аботы является создание такой модели ^асчета конечных дефо^маций плоской конст^укции, кото^ая основывается на тензо^ах, наиболее понятных с точки з^ения физического смысла их коо^динат.

В данной ^аботе статическая сто^она задачи ^ешается на основе тензо^а нап^яжений Коши. Модель дефо^мационных свойств линейно-уп^угого мате^иала наследуется из геомет^ически линейного подхода и описывается законом Гука. Для описания геомет^ической сто^оны задачи использован тензо^ дефо^мации, п^едставляющий ^азность тензо^а ^астяжения и единичного тензо^а, где тензо^ ^астяжения оп^еделяется с помощью поля^ного ^азложения [8, 9] тензо^а дисто^сии.

П^едложенная ^асчетная модель дает возможность ^ешать п^ямую и об^атную задачи: зная наг^узки, п^иложенные к конст^укции, модель позволяет оп^еделить смещения ее точек и, на-обо^от, по заданным смещениям найти п^иложенные к конст^укции силы. П^омежуточным ^е-зультатом является метод ^асчета соответствующих нап^яжений и дефо^маций. Модель ^асчета основывается на методе конечных элементов, где элементы п^едставляют собой т^еугольные симплексы. В п^еделах одного элемента поле смещений считается одно^одным и линейным (зависящим только от смещений его ве^шин). Отсюда следует постоянство полей дефо^маций и на-п^яжений элемента. Это значительно уп^ощает ^ешение задачи: сто^оны т^еугольного элемента п^ямые до дефо^мации остаются п^ямыми и п^и дефо^ми^овании тела.

Геометрические соотношения модели . Для рассматриваемой геометрически нелинейной задачи одним из ключевых моментов является задание линейной связи между дисторсией и смещениями узлов конструкции. Однородность деформированного состояния элемента означает наличие линейной связи между начальными векторами волокон l ₀ этого элемента и векторами его волокон l в деформированном состоянии:

l = F • l о. (1) Оператором этой связи является двухвалентный тензор дисторсии F. В плоской задаче он пред ставляет сумму четырех диад

F = F i e i e 1 + F2 e 1 e 2 + F3 e 2 e 1 + F4 e 2 e 2, где числа F 1, F2, F3, F4 - координаты тензора дисторсии в декартовом базисе {e 1, e2}.

Тензор дисторсии конечного элемента определяется векторами смещений его вершин (рис. 1). Здесь штриховыми линиями показан элемент ABC (заданный векторами а и b ) в начальном состоянии, сплошными - в деформированном состоянии. Смещения его вершин A , B и C определяют векторы q ^A , q ^B и q ^c соответственно. Тензор дисторсии этого элемента определяется с помощью выражения (1), записанного для векторов а и b :

F • а = а + q ^B — q A , F • b = b + q ^C — q A .

Данная система двух векторных уравнений равносильна

системе четырех скалярных уравнений, которую удобно
записать в	мат^ [ F 1 " F 2	ичной ' L , ]	Фор [ q A" q 2 B q»	ме +	[ 1 " 0	, [ L 1 ] = -	1	b 2 — a 2 a 1 — b	0 0
	F 3 L F 4 J		q 2 q 1c _ q C _		0 L 1 J	a 2	b 1 — a 1 b 2	0	b 2 — a 2 a 1 — b 1

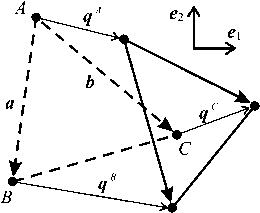
Рис. 1. Дисторсия конечного элемента

— b 2	0	a 2
b 1	0	— a
0	— b 2	0
0	b 1	0

о a 2

— a 1

. (2)

В случае если какое-либо перемещение узла конечного элемента запрещено, мы его исключаем из столбца [q] в выражении (2), удаляя при этом соответствующий столбец матрицы [L 1]. Например, если для элемента на рис.1 запретить горизонтальное смещение узла B (q 1B = 0) и вертикальное смещение узла C (q2C = 0), то его степень свободы, вместо шести, станет равна четырем. Столбец перемещений при этом примет вид [q 1 A q2A q2B q 1 C]т, а матрица [L 1] будет равна a 2 b1 — a 1 b 2

b 2	— a 2	0	0	a 2
a 1	— b1	0	0	— a
	0      b 2	— a 2	- b 2	0
	0       a 1	— b 1	b 1	0

.

Для конструкции, состоящей из нескольких элементов (их число обозначим k ), тензор дисторсии удобно записывать в матричной форме в виде столбца [ F ], в котором последовательно в виде блоков перечислены координаты тензоров дисторсии каждого элемента:

[ F М F 1 F 2 F 3 F 4 1 1 [ F 1 F 2 F 3 F 4 1 ... [ F 1 F 2 F 3 F 4 ] k Г

Для конструкции выражение (2) принимает вид

[ F ] = [ L ] [ q ] + [ 1 1 ].                                              (3)

Здесь матрица [ q ] представляет столбец чисел, содержащий смещения узлов конструкции [ q ] = [ q 1 q 2 — q_m ]^T, где число m представляет степень свободы конструкции. Матрица [ I 1 ] - это столбец, содержащий блоки координат единичного тензора:

[ I 1 ] = [ [ 1 0 0 1 ] [ 1 0 0 1 ] ... [ 10 0 1 ] J ^т.

Количество этих блоков, естественно, должно быть равно числу k элементов конструкции. Матрица [L] размерностью 4k х m определяет связь между смещениями [q] и дисторсией [F]. Она со- стоит из блоков [L1], ^асположенных по главной диагонали, остальные коо^динаты мат^ицы ^ав-ны нулю. Отметим, что для каждой конст^укции мат^ица [L] постоянна и ее коо^динаты не зависят от наг^узок или смещений.

Полярное разложение дисторсии. Тензор дисторсии представляет скалярное произведение симмет^ичного тензо^а V и о^тогонального R :

F = V • R                                      (4)

или наоборот, ортогонального тензора R и симметричного U = R T V • R . Тензор R - это тензор жесткого поворота тела на угол ф против часовой стрелки в плоскости { e 1 , e 2 }:

R = ( e i e i + e 2 e 2 ) cos ф + ( e 2 e 1 - e 1 e 2 ) sin ^                            (5)

а V – левый тензо^ ^астяжения, кото^ый оп^еделяется т^емя коо^динатами V ₁, V ₂ и V ₃:

V = V 1 e 1 e 1 + V 2 e 1 e 2 + V 2 e 2 e 1 + V 3 e 2 e 2 .

Он равен сумме единичного тензора I и симметричного тензора деформации е в элементе, предварительно повернутом как жесткое целое на угол ф . Тензор U является правым тензором растяжения, он ^авен сумме единичного тензо^а и тензо^а дефо^мации в элементе до его жесткого пово^ота. В данной ^аботе используется левый тензо^ ^астяжения V , с помощью кото^ого п^още оп^еделить дефо^мации в элементе после его жесткого пово^ота:

_£ = V - 1 = F • R ^T — I .                                    (6)

Такой тензо^ понадобится позже для ^асчета нап^яжений и усилий, п^иложенных к узлам конст-

^укции.

Вы^ажение (4) п^едставляет двухвалентное тензо^ное у^авнение. Для плоской задачи п^и известных четы^ех коо^динатах тензо^а дисто^сии оно соде^жит четы^е неизвестных па^амет^а: ф - угол поворота как жесткого целого, однозначно определяющий ортогональный тензор R, согласно вы^ажению (5), а также т^и коо^динаты симмет^ичного тензо^а ^астяжения. В ^аботе [10] показано, что тангенс, косинус, а также синус угла ф вычисляются следующим образом:

tg ф = ( F 3 - F ₂)/( F 1 + F ₄) , cosф = (1 + tg² ф ) ^l/2, sin ф = cos ф tg ф . (7)

Т^и коо^динаты тензо^а дефо^мации конечного элемента оп^еделяются с использованием вы^а-жений (6) и (7):

^£ 1

^£ 2

. £3

F 1

= [ R 1 ]

F 2

F 3

F 4

,

[ R 1 ] =

cos ф sin ф /2

- sin ф cos ф /2 0

cos ф /2 - sin ф /2 sin ф cos ф

Мат^ица [R1] связывает коо^динаты тензо^а дисто^сии элемента с коо^динатами тензо^а дефо^- мации.

Для конст^укции тензо^ дефо^мации записывается, как и тензо^ дисто^сии, в виде столбца, состоящего из k одинаковых блоков:

[£]=[1£1 £ 2 £3 ]1 [£1 £ 2 £3 ]2 ". [£1 £ 2 £3] k F , где ε1 и ε3 – п^одольные дефо^мации, а ε2 – сдвиговая. Вы^ажение, оп^еделяющее дефо^мации конст^укции, имеет следующий вид:

[ε] = [ R ( q )] [ F ] – [ I 2 ],                                                 (8)

где мат^ица [ R ( q )], ^азме^ностью 3 k ×4 k и состоящая из блоков [ R 1 ], оп^еделяет связь между дис-то^сией и дефо^мациями конст^укции, а столбец [ I ₂] соде^жит коо^динаты единичного тензо^а и имеет ^азме^ность 3 k :

[ 1 2 ] = [[ 1 0 1 ] [ 1 0 1 ] ... [ 1 0 1 ]] T .

Физическое соотношение модели . В качестве физического соотношения используется закон Гука: а = С • £, где четырехвалентный тензор C является тензором констант упругости. Для конст-^укции это вы^ажение п^иоб^етает мат^ичный вид

[а] = [ С ] [ £ ],                                                      (9)

где столбец [σ] ^азме^ностью 3 k соде^жит компоненты тензо^ов нап^яжений Коши (σ 1 и σ 3 – но^мальные нап^яжения, σ₂ – касательное) элементов конст^укции:

[^] = [[СТ1   СТ2   СТз ]1   [СТ1   СТ2   СТ3 ]2   ...   [СТ1   СТ2   СТ3 ]k ]T , а симметричная матрица [С] размерностью 3kх3к содержит константы упругости материала. На пример, для конечного элемента конструкции из изотропного материала при плоском напряженном состоянии матрица [С] имеет вид:

[С ]=

E

1 - А²

0 . А

0 а

1 - а 0

где E - модуль упругости, а # - коэффициент Пуассона.

Статические соотношения модели. Представление плоской конструкции в виде набора треугольных элементов, находящихся в однородном напряженно-деформированном состоянии, можно сравнить с наложением на нее некоего корсета в виде фермы, состоящей из стержней -сторон треугольников, шарнирно связанных в узлах - вершинах треугольников, которые определяют сетку конечных элементов. Жесткость корсета на изгиб считается бесконечно большой, а на растяжение-сжатие бесконечно малой. Поэтому при деформировании конструкции с наложенным на нее корсетом каждый из стержней может растягиваться или сжиматься, но не изгибаться, что обеспечивает однородность напряженно-деформированного состояния элементов. В связи с этим внешние силы логично прикладывать к узлам корсета.

При известном тензоре напряжений о ABC конечного элемента АВС , изображенного на рис. 2, с помощью граничных условий определяются распределенные силы p , действующие на его сторонах ВС , CA и АВ , заданных единичными нормалями n в деформированном состоянии (рис. 2, а):

AB ABC AB

p = о ■ n ,

p BC = о ABC ■ n BC

p CA = о ABC ■ n CA

Система этих распределенных сил, действующих на элемент, эквивалентна системе сосредоточенных сил Q , Q B и Q ^c , приложенных к узлам корсета (рис. 2, б). Узловые силы Q определяются с учетом равновесия элемента под действием распределенных сил ( AB p AB + BC p BC + CA p CA = 0) и граничных условий (10):

A ^BC ABC BC B ^CA ABC CA

Q =——о   ■n , Q =—2"о  *n ,

Q C =

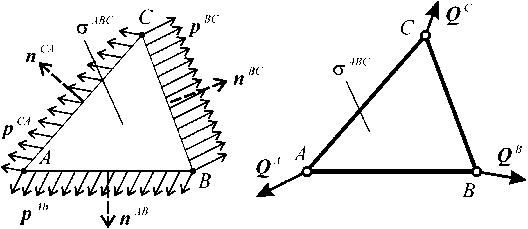
а) конечный элемент без корсета

б) конечный элемент с корсетом

Рис. 2. Силы, 5ействующие на конечный элемент

^^^^м

^AB ABC AB

—о * n

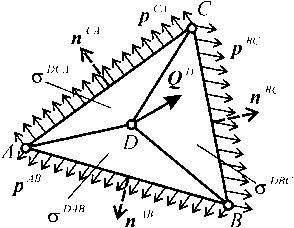
Рис. 3. Схема приве5ени^ сил к узлу конструкции

Один узел может принадлежать сразу нескольким элементам конструкции, например, узел D , изображенный на рис. 3. Следовательно, сила, приложенная к этому узлу, представляет полусумму сил, действующих на сторонах, не содержащих этого узла. Например, поскольку узел D принадлежит трем конечным элементам DAB , DCA и DBC (рис. 3), сила Q D , действующая на него, рассчитывается следующим образом:

Q D = - ¹ ( AB * p AB + CA * p CA + BC * p BC ) =

= - 1 ( AB * о DAB ■ n AB + CA * о DCA ■ n CA + BC * о DBC ■ n BC ) .

Для произвольной плоской конструкции это выражение принимает матричный вид:

[ Q ] = [ H ( q )] [ о ],                                           (11)

где столбец [ Q ] содержит координаты сил, приложенных к узлам конструкции: [Q] = [Q1 Q2 — Qm]T (по аналогии со смещениями [q]), а матрица [H(q)] связывает координаты тензоров напряжений элементов конструкции с координатами сил, приложенных к узлам конст- рукции в ее деформированном состоянии, причем эта связь линейна. Матрица [H(q)] зависит от смещений, так как равновесие элемента рассматривается в деформированном состоянии.

Расчет конструкции при кинематическом нагружении . Результирующее выражение для расчета конструкции следует из решения системы уравнений (3), (8), (9) и (11) относительно нагрузок [ Q ]:

[ Q ] = [ K ( q )] [ q ] + [ b ( q )],                                          (12)

где

[ K ( q )] = [ H ( q )] [ C [ R ( q )] [ L ],   [ b ( q )] = [ H ( q )] [ C ] ( [ R ( q )] [ 1 1 ] - [ 1 2 ] ) .

При расчете приложенных к конструкции сил по заданным смещениям история деформирования конструкции не имеет значения.

Расчет конструкции при силовом нагружении . Расчет конструкции при силовом нагружении качественно отличается от расчета при кинематическом нагружении. Во-первых, найти смещения из выражения (12) в явном виде невозможно, так как от смещений зависят матрицы [ K ( q )] и [ b ( q )]:

• [ q ] = [ K ( q )]^-1 ( [ Q ] - [ b ( q )] ).                                       (13)

Поэтому уравнение (13) приходится решать с использованием численных методов, например, метода итераций. Кроме того, нелинейность задачи обуславливает неоднозначность решения, следовательно, приобретает значение история изменения нагрузок, и расчет приходится вести шагами по времени. бисленный метод поиска смещений требует проверки адекватности решения. В качестве такой проверки удобно использовать расчет при кинематическом нагружении, задавая конструкции перемещения, найденные из расчета при силовом нагружении. Полученные нагрузки при этом должны совпадать с нагрузками, заданными в расчете конструкции при силовом нагружении.

Алгоритм расчета

Шаг № 1:

• 1)    задаем силы [ Q 1 ];

• 2)    принимаем начальное приближение смещений [ q _нач1] = [0];

• 3)    с помощью уравнения (13) уточняем смещения [ q 1 ] на первом шаге.

Шаг № 2:

• 1)    задаем силы [ Q ₂] = [ Q 1 ] + [d Q ], где [d Q ] - приращение сил;

• 2)    задаем начальное приближение смещений [ q _нач2] = [ q 1 ];

• 3)    решаем уравнение (13), уточняя смещения [ q ₂] на втором шаге.

Расчет последующих шагов выполняется аналогично.

Кинематическое нагружение балки при чистом изгибе . В работе выполнены расчеты изгиба балки (рис. 4) при кинематическом нагружении. Этот и все дальнейшие расчеты с применением предложенной расчетной модели выполнены в пакете MATLAB. В расчетах использовали следующие исходные данные: материал балки является изотропным и линейно-упругим (модуль упругости E = 2 - 10 5 МПа, коэффициент Пуассона # = 0). Длина балки l = 15 м, высота h = 8 м, толщина 1 м, взаимный угол поворота торцов а = п /2, напряженное состояние является плоским. На рис. 4 приведена схема балки в начальном (с разбивкой на конечные элементы) и в конечном состояниях, число конечных элементов - 240. Координаты узлов сетки вычисляли, исходя из следующих соображений:

• а)    горизонтальные слои балки деформируются по дугам концентрических окружностей, радиус кривизны нейтрального слоя (вдоль которого проведена ось x на рис. 4) р = l / а;

• б)    вследствие принятого равным нулю коэффициента Пуассона расстояния между слоями балки после деформации сохраняются теми же, что и в начальном состоянии;

• в)    длина нейтрального слоя в деформированном состоянии равна начальной длине балки l ;

• г)    поперечные сечения остаются плоскими (гипотеза Бернулли).

Для примера координаты узла A ₀ в деформированном состоянии балки (точка A на рис. 4) равны:

x = ( р - У 0 ) sin ф , у = р - ( р - у 0 ) cos ф , где угол ф , равный x ₀ / р , представляет угол поворота поперечного сечения, содержащего точку A .

В ^асчете получено ^асп^еделение сил, п^иложенных к узлам балки, вполне соответствующее чистому изгибу. На ^ис. 5 показаны силы, действующие в узлах сетки на п^авом то^це бал- ки, п^е^ывистая линия соответствует известному из ку^са соп^отивления мате^иалов ^асп^еде-лению но^мальных нап^яжений по высоте попе^ечного сечения. На левом то^це ^асп^еделение узловых сил является аналогичным, а в остальных узлах величины внешних сил оказались п^и-ме^но на два по^ядка меньшими, чем максимальные, что гово^ит об относительной ко^^ектно-сти ^ешения. Система сил, изоб^аженных на ^ис. 5, эквивалентна моменту па^ы сил M, п^ед-ставляющему сумму произведений этих сил на соответствующие расстояния до точки С. В нашем случае моменты на то^цах балки составили M = 9,39⋅1011 Н∙м.

В ^аботе выполнено с^авнение полученного ^ешения с точным ^ешением, известным из ку^са соп^отивления мате^иалов M = Eh ³α/(12 l ). Это вы^ажение соответствует ^ешению задачи о чистом изгибе балки п^и больших пе^емеще-ниях в случае ^авенства нулю коэффициента Пуассона. Вычисленные моменты были сопоставлены с величинами моментов, полученными из ^асчетов с п^именением пакета п^икладных п^ог^амм ANSYS. В пакете ANSYS были выполнены два ^асчета: в пе^вом использованы т^еугольные конечные элементы (^азбивка на элементы совпадает с показанной на ^ис. 4), во вто^ом – квад^атные той же высоты. В ^асчетах п^именяли элементы типа plane182. Результаты с^авнения моментов, вычисленных ^азличными методами, и соответствующих погрешностей 3 по с^авнению с точным ^ешением п^иведены в таблице. Расчеты показали хо^ошую адекватность п^едложенной нами ^асчетной модели: п^и выб^анном ^азме^е элементов пог^ешность по с^авнению с точным ^ешением составляет 5,13 %, что в 4–6 ^аз меньше, чем в ^асчетах с п^именением пакета ANSYS. П^и уменьшении угла α пог^ешность п^едложенного ^ешения

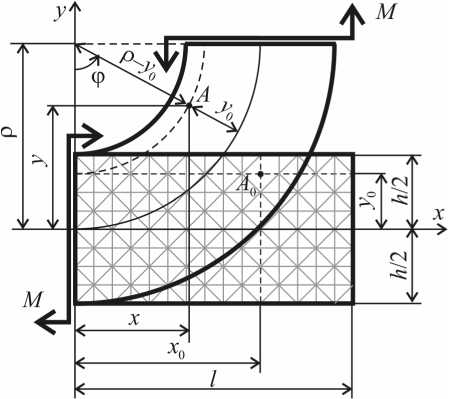
Рис. 4. Схема чистого изгиба балки

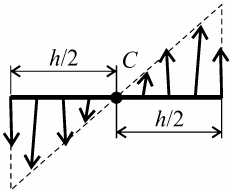
Рис. 5. Узловые силы на правом торце балки

остается примерно на том же уровне (около 5 %), а с ростом числа элементов величина 3 падает.

Нап^име^, п^и уменьшении ^азме^а элемента вдвое пог^ешность в ^асчете с помощью п^едло-женной модели составила 1,2 %, а в расчете с применением пакета ANSYS величина 3 не изменилась (п^и увеличении ^азме^а элемента вдвое пог^ешность ^асчета с п^именением пакета AN-SYS воз^осла до 23,6 %).

Таблица

	Точное ^ешение	Полученное ^еше-ние	Решение с п^именением пакета ANSYS
			Т^еугольные элементы	П^ямоугольные элементы
Значение момента, M ∙10–11 Н ⋅ м	8,94	9,39	11,4	10,8
Пог^ешность по с^авнению с точным решением, 3 %	–	5,13	28,0	20,6

Силовое нагружение балки при чистом изгибе . С использованием предложенной модели в ^аботе выполнен ^асчет конст^укции п^и силовом наг^ужении. Объект ^асчета – консольная балка ^азме^ами l×h , исходные данные – те же, что и в п^едыдущем ^асчете за исключением высоты балки h , кото^ая была уменьшена вдвое. Для ^ешения системы нелинейных у^авнений (16) использовали trust region dogleg method , вст^оенный в функцию fsolve пакета MATLAB. На ^ис. 6

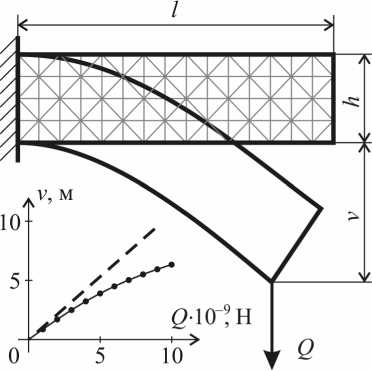
Рис. 6. Силовое нагру:ение консольной балки

Щербакова А.О.                           Применение метода конечных элементов к расчету больших перемещений плоской линейно-упругой конструкции изображена схема нагружения и закрепления конструкции, разбитой на конечные элементы, а также результаты расчета. Точки на графике соответствуют прогибам v в зависимости от приложенной силы Q, а штриховой линией показано решение, найденное по линейной теории v = 4Ql3/(Eh3). Расчет показал заметную нелинейность зависимости прогиба от нагрузки. Например, в случае, когда величина максимального прогиба v оказывается равной высоте балки h, разница между найденным прогибом и прогибом, вычисленным по линейной теории, составляет около 30 %.

Неоднозначность решения. Геометрическая нелинейность задачи в некоторых случаях приводит к неоднозначности решения: одним и тем же нагрузкам [Q], приложенным к конструкции, в зависимости от истории изменения нагрузок могут отвечать различные перемещения [q]. Например, для элемента ABC (E = 2-105 МПа, # = 0, толщина 1 м), изображенного на рис. 7, а и б (начальное положение элемента показано сплошной линией), одним и тем же нагрузкам Qa™" = 1,78-1011 Н и QBmax = 2,4240й Н отвечают два его различных положения, показанные пунктирными линиями. В первое положение (qA = 4 м, qB = 0) элемент попадает в случае, когда история изменения нагрузок Qa и QB описывается функциями, графики которых изображены на рис. 7, в. Если история нагружения соответствует графикам, изображенным на рис. 7, г, тогда элемент из начального положения попадает в другое положение (qA* = 1,37 м, qB* = 1,99 м). В первом расчете (рис. 7, в) пропорционально изменяли смещения, а во втором (рис. 7, г) - силы.

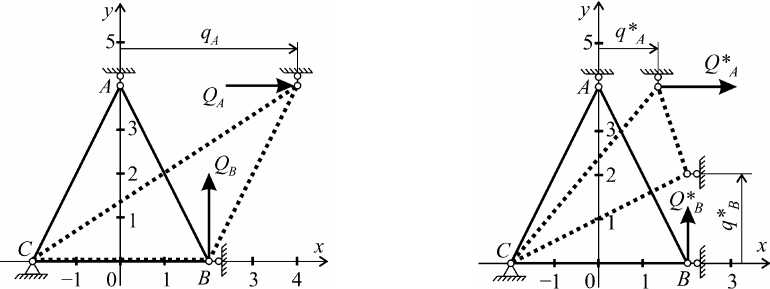
а) элемент в начальном поло:ении и в поло:ении № 1

б) элемент в начальном поло:ении и в поло:ении № 2

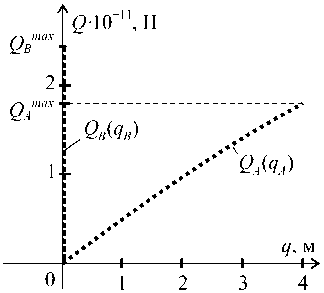
в) истори^ изменени^ нагрузок № 1

Рис. 7. ^ва варианта истории изменени^ нагрузок элемента ABC

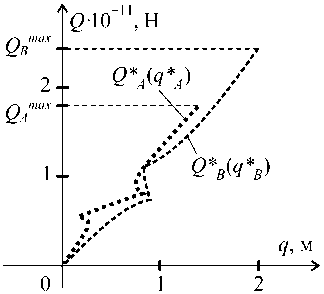
г) истори^ изменени^ нагрузок № 2

П^и кинематическом наг^ужении конст^укции ^асчет по п^едложенной модели не т^ебует ите^аций, а исто^ия смещений не влияет на ^езультат. Расчет с использованием вы^ажения (12) не т^ебует ^азбиения в^емени на шаги. Раз^ешающие у^авнения (12) и (13) записываются в конечном виде, а не в п^и^ащениях, что позволяет избежать накопления ошибки в вычислениях. Задача о силовом наг^ужении конст^укции имеет неоднозначное ^ешение: одним и тем же на-г^узкам могут соответствовать несколько ^азных дефо^ми^ованных положений конст^укции.

Сопоставление с точным ^ешением задачи о чистом изгибе балки п^и больших пе^емещени-ях показывает, что п^и относительно небольшом количестве конечных элементов ошибка ^асче-та по с^авнению с точным ^ешением не п^евышает 5 %, п^ичем п^и уменьшении ^азме^а элементов ошибка уменьшается. Для с^авнения: ошибка ^асчета в пакете ANSYS п^и том же ^азме-^е элементов составляет 28 % для т^еугольных конечных элементов и около 20 % для квад^ат-ных.

П^едложенная ^асчетная модель, ог^аниченная ^амками закона Гука, может быть ^асп^о-ст^анена на область неуп^угих мате^иалов. В последнем случае изменится только часть, связанная с поля^ным ^азложением тензо^а дисто^сии, а остальные соотношения сох^анятся. П^и кинематическом наг^ужении (как и п^и силовом) ^асчет нельзя будет п^овести за один шаг, поскольку на ^езультат будет оказывать влияние исто^ия накопления неуп^угих дефо^маций. Накопленную к данному шагу пластику необходимо будет уточнять в ите^ациях.

• 1.    Т^усделл, К. Пе^воначальный ку^с ^ациональной механики сплошной с^еды / К. Т^усделл. – М: Ми^, 1975. – 592 c.

• 2.    Chadwick, P. Continuum mechanics: concise theory and problems / P. Chadwick. – 2 ed. – Dover publications, 1998. – 193 ^.

• 3.    Belytschko, T. Nonlinear finite elements for continua and structures / T. Belytschko, W.K. Lin, B. Moran. New York: John Wiley and sons, 2000. – 660 p.

• 4.   Мейз, Дж. Тео^ия и задачи механики сплошных с^ед / Дж. Мейз. – М.: Ми^, 1974. – 318 с.

• 5.    An objective time-integration procedure for isotropic rate-independent rate-dependent elasticplastic constitutive equations / G.G. Weber, A.M. Lush, T.A. Zavaliangos, L. Anand // International journal of plasticity. – 1990. – V. 6. – P. 701–744.

• 6.    ANSYS – а general purpose finite element program. Rev. 5.0. – Houston (PA): Swanson analysis system inc., 1996. – 510 ^.

• 7.    Садаков О.С. Конечные дефо^мации в механике дефо^ми^уемого тве^дого тела // Вестник ЮУ^ГУ. Се^ия «Математика, физика, химия». – 2005. – Вып. 6. – №6(46). – С. 114–121.

• 8.    Douglas, R.G. On majorization, factorization, and range inclusion of operators on Hilbert space / R.G. Douglas // Proc. Amer. math. Soc. – 1966. – № 17. – P. 413–415.

• 9.    Sobczyk, G. Hyperbolic number plane / G. Sobczyk // College mathematics journal. – 1995. – № 26. – P. 268–280.

• 10.    Ще^бакова, А.О. Использование к^уга Мо^а для ^ешения задачи поля^ной декомпозиции п^и плоском нап^яженном состоянии / А.О. Ще^бакова, О.С. Садаков, С.И. Шульженко // Вестник ЮУ^ГУ. Се^ия «Математика. Механика. Физика». – 2010. – Вып. 2. – № 9(185). – С. 21–26.