Применение метода максимального правдоподобия для обработки сигналов в цифровых системах обмена информацией

Цитирование: Шостак С. В. Применение метода максимального правдоподобия для обработки сигналов в цифровых системах обмена информацией / С. В. Шостак, А. В. Бенгард, Е. А. Свердлов, Г. В. Дорофеев, П. А. Стародубцев // Журн. Сиб. федер. ун-та. Техника и технологии, 2025, 18(3). С. 428–434. EDN: YMTKME

В современных системах обмена информацией основная ее часть передается в цифровом виде. Причём передается не аналоговый модулированный сигнал, а набор целых чисел, которые принимают значение из некоторого фиксированного конечного множества [1–3]. Эти числа, называемые символами, поступают от источника информации с определенной символьной скоростью. При этом выполняется основной принцип передачи дискретной последовательности символов – каждому из возможных значений символа сопоставляется некоторый набор параметров несущего колебания, т.е. проводится модуляция несущего колебания [1, 2]. Способ модуляции, когда параметры несущего колебания меняются скачкообразно, определяется как манипуляция. Эти параметры поддерживаются постоянными в течение определенного интервала до прихода следующего символа. В зависимости от того, какие параметры изменяются, различают амплитудную (АМн), фазовую (ФМн), частотную (ЧМн) и квадратурную (КАМ) манипуляции [1–3].

Особенность цифровых систем связи состоит в том, что задачей приемника является не точное воспроизведения сигнала, а определение на основе принятого искаженного шумами и помехами сигнала, какой из конечного набора был излучен передатчиком [1–3]. При распространении информационного сигнала в канале передачи его форма может искажаться за счет собственных помех канала и, возможно, преднамеренных помех. Это приводит к ошибкам в детектировании символов. Поэтому задачу определения принятого символа следует рассматривать как задачу оценки параметров модулированного сигнала.

Рассмотрим на примере сигналов с квадратурной манипуляцией (КАМ, или QASK) решение такой задачи на основе известной теоремы.

Как известно, в случае квадратурной манипуляции каждому из возможных значений дискретного символа ставится в соответствие пара величин – амплитуда Am и начальная фаза φ m несущего колебания [1–3]. Такой сигнал в дискретном виде имеет вид [1–3]

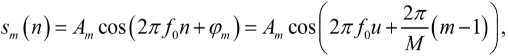
где Am – амплитуда m-го символа; /о = ~ – нормализованная несущая частота; fs – частота дискретизации; /о – несущая частота; n – номер отсчета в области времени, n = 0 ÷ N – 1; N – число отсчетов;

M ’

– начальная фаза для m -го символа; m = 0 ÷ M – номер символа;

M – число символов.

В реальной обстановке при воздействии аддитивного шума, под которым будем понимать шум канала + помехи xm («) = 4, cos(2я/0и + фт ) + ®m (w),                                    (2)

где ω( n ) – искажающее воздействие (шум канала + помеха).

Для таких условий надо понимать не измерение параметров, а их оценки. Поэтому найдем оценки потенциальной точности параметров гармонического сигнала в (2) на основе теоремы Рао-Крамера, которая устанавливает нижнюю границу для дисперсии ошибки оценки параметров без относительно используемого метода оценки, считая, что ω( n ) – белый гауссов шум [4–6].

Для упрощения рассуждений перепишем (2) в следующем виде:

х(и) = A cos(2я/₀п + (р) + со(п),                                         (3)

Требуется оценить A , f 0 , φ. Для этого сформируем информационную матрицу Фишера [4, 5]

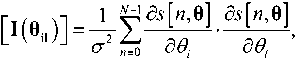
где σ ² – дисперсия шума; i , l = 1, 2, 3; θ = [ A , f 0 , φ] ^T – вектор параметров.

Предположение, что f ₀ достаточно удалено от 0 и ½, позволяет сделать определенные упрощения, основанные на аппроксимации [4]

I лм

— = £ и' sin (4я/0п + 2<р)« 0, n=0

i 2 п¹ cos {4я^п + 2^0

для i = 0, 1, 2. Используя эту аппроксимацию и подставляя a = 2 πf 0 n + φ , имеем

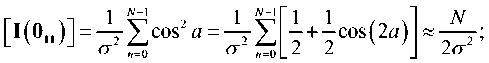
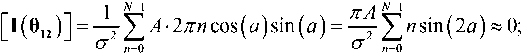
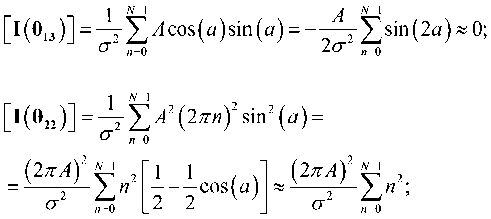
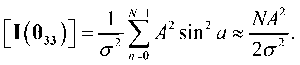
В результате информационная матрица Фишера становится

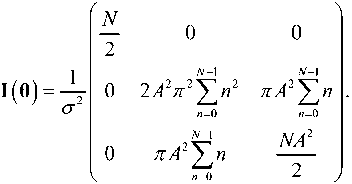
После инверсии I (θ) с использованием равенств

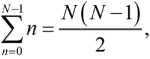
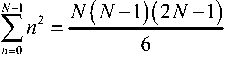
получим

var A > — ’ N

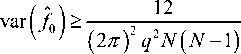
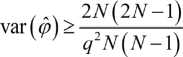
где r=^ – отношение сигнал/шум.

Необходимо заметить, что граница неравенства Рао-Крамера для частоты f0 уменьшается с увеличением отношения сигнал/шум и уменьшается пропорционально -^, делая ее чувстви- тельной к длине сигнала.

Получение оценок рассмотрим на основе следующей теоремы.

Теорема 2 [4–6]. Если данные наблюдения X описываются общей линейной моделью вида

X = H θ + W ,                                                   (18)

где H – известная N × p матрица с N > p и ранга p, θ есть p × 1 вектор оцениваемых параметров, W есть N × 1 вектор шума с плотностью функции распределения ℕ(O, C), тогда оценка по методу максимального правдоподобия есть где C - ковариационная N х N матрица шума; ()-1 - оператор обращения.

При этом полученная оценка эффективна, достигает границ неравенства Рао-Крамера и является несмещенной оценкой с минимальной дисперсией. Плотность функции распределения оценки имеет вид

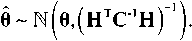
Для приложения результатов теоремы 2 проведём некоторые преобразования сигнала xm ( n ), для чего представим выражение (2) следующим образом:

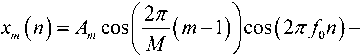
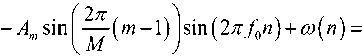
= ат cos(2л-/0и) + bm sin (2^f0n) + со(п), где

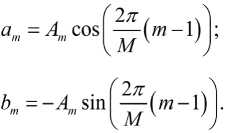
Из выражения (21) следует, что для определения символа на плоскости, т.е. «в созвездии», необходимо получить оценки am и bm, которые удобно представлять в виде комплексного числа в алгебраической (am + jbm) или комплексной форме

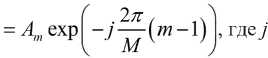
– мнимая

единица.

В нашем случае представим выражение (21) в векторно-матричном виде хт (°)

/Л^Л ад

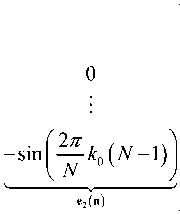
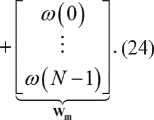
Далее выразим (24) в более компактном виде

X = H θ + W ,

где X - N х 1 вектор принятого сигнала; H = [ e i ( n ) e ₂( n )] - N х 2 известная матрица; 9 = [ a m b m ]^T - 2 х 1 вектор параметров; [] T - оператор транспонирования; W - N х 1 вектор аддитивного шума.

Выражение (25) представляет линейную модель формирования символа. В результате обработки принятого сигнала X ( n ) , представленного выражением (25), требуется получить оценку вектора θ.

Из проведенных рассуждений следует, что оценку параметров am и bm целесообразно проводить согласно выражению (19). После получения оценок и несложно найти оценки амплитуды и начальной фазы соответственно m ’

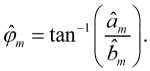
В частном случае, когда ω( n ) – белый шум, выражение (19) примет следующий вид:

нтх.

Соответственно, выражение для плотности функции распределения (28) становится

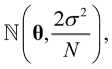
где σ2 – дисперсия белого шума.

В реальных условиях на длительности сигнала шум, как правило, считается стационарным, хотя и не всегда белым. Свойство стационарности шума позволяет оценивать его первые два момента для получения ковариационной матрицы C . Следует также отметить, что умножение входного сигнала X на C ^-1 в (19) приводит к отбеливанию искажающей составляющей W .

Приложение метода максимального правдоподобия рассмотрено на примере обработки сигналов с квадратурной манипуляцией в условиях воздействия аддитивного шума. При этом предполагается, что шум может быть окрашенным. Для применения метода максимального правдоподобия модель формирования таких сигналов представлена в линейном векторноматричном виде (25). Проведен анализ потенциальной точности оценки информационных параметров сигнала (3) на основе теоремы Рао-Крамера [3], для чего была определена информационная матрица Фишера. Затем после её обращения получены выражения для дисперсии параметров информационного сигнала. Представление сигнала в векторно-матричном виде позволяет для его обработки применять результаты теоремы 2 – выражение (19). Показано, что в частном случае, когда искажающее воздействие – белый шум, оценка параметров проводится согласно выражению (28). Изложенный способ оценки параметров может быть также распространён и на другие виды модуляции сигналов в цифровых системах передачи, для чего необходимо, естественно, формировать матрицу H в выражении (25) соответствующего вида.