Применение метода многих масштабов к задаче о возникновении концентрационной конвекции в прямоугольной области пористой среды

4.0. Чтобы просмотреть копию этой лицензии, посетите

Использование природных геологических систем в производственной и промышленной деятельности человека сопряжено с рядом осложняющих факторов. Эти системы состоят из различных пород, грунтов и почв, которые являются пористыми средами. При фильтрации жидкости через эти среды могут происходить процессы, в результате которых частицы твердых веществ и примесей переносятся жидкостью, а также частично растворяются в ней. Эти процессы могут привести к техногенным катастрофам. Учет этих процессов при добыче и обработке полезных ископаемых на рудниках помогает предотвратить опасные последствия, для этого, например, может быть рассчитана прочность конструкции при добыче сырья из пластов.

Риск загрязнения почвы возникает при эксплуатации полигонов, на которых собираются бытовые и промышленные отходы. Снег и дождевая вода с высокой концентрацией загрязнений могут проникать в грунт, перенося с собой вредные вещества. Это может привести к загрязнению водных объектов, включая источники питьевой воды.

Проблемы, связанные с переносом примесей в пористой среде, возникают при очистке фильтров и разработке строительных материалов, когда важно поддерживать чистоту материала для сохранения его свойств. В таких системах могут быть значительные различия в плотности жидкости и примесей, что приводит к неустойчивости и возникновению концентрационной конвекции, а также усложняет процесс транспорта веществ. Одной из первых работ, в которой экспериментально наблюдалась концентрационная конвекция в пористых средах, является [1].

Основываясь на вышеперечисленных причинах, можно сказать, что изучение переноса примеси с учетом адсорбционно-десорбционных свойств необходимо для большого числа технологических фильтрационных процессов, а также для предотвращения экологических катастроф. Для изучения сорбции в пористых средах существует стандартный эксперимент, заключающийся в прокачке конечного объема смеси через массив пористой среды при заданном перепаде давления или при фиксированном расходе. В ряде подобных экспериментов [2] обнаруживалось влияние гравитационной неустойчивости на ход экспериментов. Исследование концентрационной конвекции для корректного учета этого влияния необходимо при подготовке и проведении экспериментов по изучению процессов сорбции в пористых средах.

Наиболее популярным подходом к описанию сорбции в пористых средах является MIM (mobile-immobile media) подход [3], заключающийся в разделении примеси на две фазы: мобильную и иммобильную. Мобильная фаза примеси – частицы, перемещающиеся вместе с потоком несущей жидкости, иммобильная фаза – частицы, осевшие на скелете пористой среды за счет, например, сил Ван дер Ваальса. Обмен примесью между фазами обычно описывается некоторым кинетическим уравнением, выбор уравнения зависит от характера взаимодействия частиц со стенками пористой среды. В литературе представлено множество форм кинетических уравнений в рамках MIM-подхода, представим наиболее распространенные из них:

Стандартная модель MIM [4] – скорости адсорбции и десорбции прямо пропорциональны концентрациям в мобильной и иммобильной фазе соответственно. Фрактальная (дробная) модель MIM [5] – предполагает, что частицы примеси, находящиеся в пористой среде, могут оставаться связанными на непредсказуемо долгие периоды времени. Распределение времени этой связанности не имеет среднего значения, что свидетельствует о субдиффузионном переносе. Следовательно, кинетическое уравнение можно выразить через линейную зависимость потока частиц в неподвижной фазе от дробной производной Капуто от концентрации частиц в подвижной фазе по времени. Данная модель имеет экспериментальное подтверждение, в основном для низких концентраций примеси [6]. Нелинейная MIM-модель с насыщением [7] – описывает транспорт в пористых средах для высоких концентраций растворенного вещества. В модели задается некоторое предельное значение концентрации иммобилизованной примеси, при котором процесс осаждения частиц (адсорбции) останавливается. В [7] этот эффект описывается кинетической моделью второго порядка, в которой скорость адсорбции прямо пропорциональна разнице между предельной концентрацией насыщения и концентрацией в немобильной фазе.

В настоящей статье решается двумерная задача устойчивости течения смеси через вытянутую прямоугольную область пористой среды. Предполагается, что горизонтальный размер области больше вертикального в 10 раз. Между вертикальными границами задается перепад концентрации и давления, на горизонтальных границах является условие отсутствия потоков несущей жидкости и примеси. Задача решается в приближении Дарси–Буссинеска [8], транспорт примеси описывается в рамках линейной MIM-модели [4].

Статья состоит из пяти разделов. В первом обсуждается актуальность исследования и приведен обзор литературы. Второй раздел посвящен постановке задачи. Третий подробно раскрывает методику решения. Четвертый раздел представляет полученные результаты. В последнем пятом разделе приведены основные выводы.

Рассматривается двухмерная задача транспорта примеси через прямоугольный массив пористой среды с отношением сторон H/L = 0.1. Фильтрация примеси происходит за счет заданного на вертикальных границах постоянного перепада давления P - P , на которых так же задается и постоянный перепад концентрации С₊ - С . На горизонтальных границах – условие непротекания несущей жидкости и непроницаемости для растворенного в ней вещества (рис. 1).

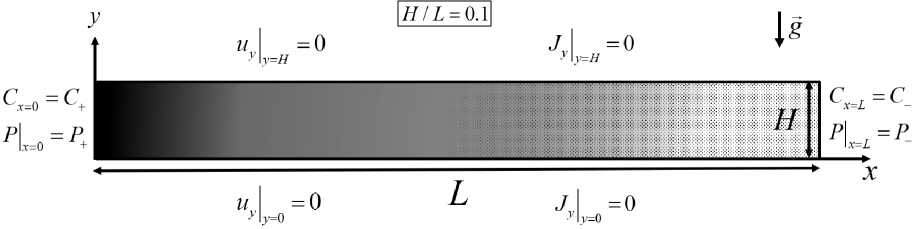
Рис. 1. Принципиальная схема решаемой задачи

Транспорт примеси моделируется в рамках MIM-подхода [3]. Концентрация примеси разделяется на две фазы мобильности: мобильную и иммобильную. Примесь в мобильной фазе может переноситься потоком несущей жидкости. Иммобильная фаза формируется частицами, осевшими (адсорбировавшимися) на стенки пор, такие частицы не могут переноситься потоком несущей жидкости. Уравнение переноса для MIM подхода (1) имеет следующий вид:

^{д(ф С +} Q ) = _div j , j = — d _у с + u с , d t                        ^{,                              ,}

где С , Q - объемные концентрации мобильной и иммобильной примеси, u - скорость фильтрации, ф - пористость среды, D - эффективный коэффициент диффузии.

Фильтрация описывается законом Дарси–Буссинеска [8], учитывающим изменение плотности раствора за счет изменения концентрации примеси. Неоднородность плотности в поле силы тяжести позволяет описать возникновение концентрационной конвекции.

Жидкость считаем несжимаемой. Математически это выражается в следующем виде:

u = - - ( v P' + p ₀ g fi c C k ) ,   P ‘ = P + p ₀ gy ,

П                                             .                    (2)

div u = 0, где u - скорость фильтрации, к - коэффициент проницаемости, п — динамическая вязкость, р0 - плотность несущей жидкости, вс — коэффициент концентрационного расширения, C - концентрация мобильной фазы, g – ускорение свободного падения, k - орт вектор оси y, P — давление жидкости, P' - полное давление жидкости (с добавком гидростатического распределения). При дальнейшем употреблении формулы (2) штрих у давления под знаком градиента будет опущен.

Уравнение (1) должно быть дополнено так называемым кинетическим уравнением, описывающим фазовый переход между фазами мобильности.

В данной работе мы используем наиболее простую линейную MIM-модель [4]:

^ Q = а( С - KQ ) ,                       (3)

dt где а - коэффициент переноса примеси, Kd -коэффициент распределения примеси.

Итоговая система уравнений, описывающая транспорт примеси в пористой среде с учетом процессов сорбции и конвекции, имеет вид:

д(ф с + Q )  ,_п._г

---- = ф D A C - u -V C ,

| Q = а ( С - K_d Q ) ,

^{8 1}                                                           (4)

U = - - (vP + Po gPcCk), п div u = 0;

В качестве граничных условий для задачи имеем постоянный перепад давления и концентрации, заданные между вертикальными границами и непроницаемые для вещества и несущей жидкости горизонтальные границы:

P ( x = 0, y , t ) = P + , P ( x = L , y , t ) = P _ ,

C (x = 0, y, t ) = C+,  C ( x = L, y, t ) = C-,

• (J - k)|      = 0,     (u - k)|

• V       /I y=0, H      ’       v       y=0=0, H’

Для удобства перепишем уравнения (4) в безразмерной форме. Для этого выберем следующие масштабы: концентрация мобильной компоненты [ С ] = С₊ — C , концентрация немобильной компоненты [ Q ] = ф ( C₊ — C ) , время [ t ] = L ² / D , длина [ l ] = L , скорость фильтрации [ u ] = ф D / L , давление [ P ] = P - P .

Тогда система (4) перепишется в безразмерном виде:

d( c + q)

—----- = A c - u • V c ,

дt

д q      a

= ac - bq, dt

u = -(PeVp + Rpck), div u = 0;

где Pe = k ( P - P ) / 0p D - диффузионное число Пекле, Rp = кр₀ g p ( C₊ - C ) / фр / — число Рэлея-Дарси, a = a L / 0 D - коэффициент адсорбции, b = a K_dL / D - коэффициент десорбции. Число Пекле Pe характеризует отношение сил давления к вязким силам, а число Рэлея–Дарси Rp отношение сил плавучести к силам вязкости. За интенсивность перехода между фазами мобильности отвечают коэффициенты сорбции ( a , b ).

Перепишем систему (6) для двухмерного случая, исключив скорость фильтрации:

д(c + q)  д2c  д2c     (дc дp  дc дp^  _   дc

=   +   + Pe ++ Rp c

д t     дx2  дy2     ^дx дx  ду дy J      дy

д q       к

= ac - bq

д t

д2 p  д2 p  Rp д c

дx2   ду2     Pe ду

Граничные условия (5) в безразмерном виде:

c (x = 0, у, t ) = 1, c (x = 1, у, t ) = 0, p (x = 0, у, t ) = 1, p (x = 1, у, t ) = 0,

Ф =_RPC|

ду             Pe |у=0,h ’

/ у=0, h

д c

ду

= 0;

у=0, h

в случае отсутствия сил плавучести (Rp = 0) задача имеет решение:

c0 (x) =   ----Pe-’ q0 (x) = ac0 (x), p0 (x) = 1 -x.               (9)

1 - e               b

При малых значениях числа Рэлея–Дарси к системе уравнений (6) может быть применен метод разложения по малому параметру.

Система уравнений (6) после введения малого безразмерного параметра s :

д ( c + q )           Л       .    R д cЛ —----- = Д c + Pe ( V p -V c ) + s^c— , д t             k                д y J д q      h p = ac - bq ,                                     (io) 8c Д p = — s^ -; д y

где Rp/Pe = р: , г - безразмерный малый параметр, Rp число Рэлея-Дарси, Pe число Пекле.

Граничные условия имеют вид:

^ p      =-e^c\ „,,  '       = 0, д y y = 0, h           y = °' h    d y y p ( x = °, y, t ) = 1,   p ( x = 1, y , t ) = °,                       (11) с ( x = °, y , t ) = 1,    с ( x = 1, y , t ) = °.

Согласно методу многих масштабов [9], искомые функции раскладываются в ряд по малому параметру:

с ( x , y , t ) = c 0 ( x ) + s c1 + s 2 c 2 + ... q ( x , y , t ) = q 0 ( x ) + s qx + s 2 q 2 + ... 2                                 (12) p ( x , y , t ) = p ° ( x ) + s p 1 + s p 2 + ... d / d t = д / d t 0 + sd / d tx + s 2 d / d t 2 + ...

В нулевом порядке распределение концентрации и давления определяются стационарным решением системы (10):

Pe - x    Pe c ° ( x ) =  ,     Pe ,   q ° ( x ) = cC ° ( x ) ,   p ° ( x ) = 1 x .                    (13) 1 — e              b

Система уравнений (10) в первом в порядке малости г имеет вид:

d( C -+ q 1 = Д с + Pe ( V p ° - V с , + V p , - V с л ) , д t ° д q      h —1 = ac 1 — bq 1,                                            (14) д t ° Д p 1 = °;

граничные условия в этом же порядке запишутся следующим образом для давления:

-<•°(x),  dpL    =—&°(x), ду y=°                ду y=h                                (15) p (°, y, t) = —^y,  p1 (1, y, t) = °; и концентрации:

= 0, Ест= ду у=0        ду у=h           .(16)

с ( 0, y , t ) = 0, с ( 1, y , t ) = 0:

Для сведения задачи к однородному виду, можно ввести замену для переменной давления:

Pi (x,у,t) = pl (x,у,t)-^c0 (x)у .(17)

В результате замены (17) граничные условия (15) становятся аналогичны условиям (16):

^д p i д у

= 0, у=0

^  = 0,

P l ( 0, у , t ) = 0,   P l ( 1, у, t ) = 0;

при таких граничных условиях задача имеет аналитическое решение в виде ряда Фурье.

Результаты

Уравнение для концентрации мобильной компоненты:

^C 1 ( x , У , t ) = E ( A nm e ^ n , m

Pe

+ Bn_me^Y t ) e 2 sin (n mx ) cos

п пу

+

^fF ^ + У nm^ в n, m у ^nm J

Pe x

sin (n mx )

cos

f ^пу '

I h J

уравнение для концентрации иммобильной фазы:

ж

q i ( ^x , у , t ) = X

n , m

ж

, a Y Fnm b ^   ²²

Pe

aeY tA    aeY 2 tB nm          nm

Pe

x в2 sin (nmx ) cos

п пу I

h

.

^ nm J

x в2 sin (nmx)cos

п пу

h

Уравнение для давления:

ж pi (x, у ) = "Z k=1

2 ^

( n² k ² + Pe² )

f k ( Pe ) P k ( у ) sin n k ,

f_k ( Pe ) =

( ^{( - 1 ) k} - 1 ) Pe² в ^Pe      J Pe )

n² n ^!  pye) — ^cth [ T J

Pk (у ) =

( 1 - ch n kh ) sh n kh

ch п ку + sh п ку ;

где показатели у ₁₂ временной экспоненты всегда меньше нуля и определяются выражением:

- a а + b + Л2 )±« а + b + А2 V - 4Л2 b nm                nm        nm

^Y 1,2 =                        о

На больших временах зависящая от времени часть решения (19) и (20) обращается в ноль и распределение концентрации определяется коэффициентами (23) и (24):

F nm

—

4- Pe3 • h (1 — ePe )2

2 п n

Pe

«

Pe z mm

4 n m e ²   ( — 1 )

4 п² m ² + 9Pe ²

7 +

⁺ h ( 1 — e^Ре

У 2 - ^ (^{П к + P}e )

к

X

( h² к ² + n²

- 1 ) ^— 1 ) Pe ² e^Ре п² к ²     ( 1 — e^Ре

Pe

1^{1 +} k ⁺ m e ^y  (4 п ²(

-

X

m ² — к ²) + Pe ² )

)      ( 4 п ² ( к + m ) 2 + Pe ² )( 4 п ² ( к — m ) ² + Pe ² )

Используя тот факт, что в момент времени t = 0 возмущения в области отсутствуют c ( x , y , t = 0 ) = 0 и q_x ( x , y , t = 0 ) = 0 можно определить коэффициенты A_nm и B nm :

A nm

B

nm

_ Y2 b+Y Fm

Y2 — Y1   b  Fm ’

• Y1  b + Y Fm.

• Y2 — Y1   b   Fnm ’

Представлены результаты расчетов при суммировании следующего количества членов рядов (19), (21) и (24): n = 0..40, m = 1..40, к = 1..100. Согласно постановке задачи, рассматривается вытянутая вдоль оси x область, поэтому отношение сторон h принимается равным 0.1. Параметр h не влияет на количество образующихся конвективных ячеек, но может влиять на интенсивность. Таким образом, чем длиннее рассматриваемая область, тем более вытянута будет одна из конвективных ячеек и тем меньше будет ее интенсивность. Величина s - это порядок отношения числа Rp/Pe = — . Для малости £ требуется, чтобы Rp <  Pe, с физической точки зрения этого можно добиться увеличением перепада давления (ростом числа Пекле – Pe) или уменьшением перепада концентрации (уменьшение числа Рэлея–Дарси – Rp). В связи с тем, что решение получено для £ <<1 при суммировании поправки с основным решением наблюдается незначительное искривление полей (рис. 2–3).

-1,5          0,5

c,(x,y)-102

-4,5

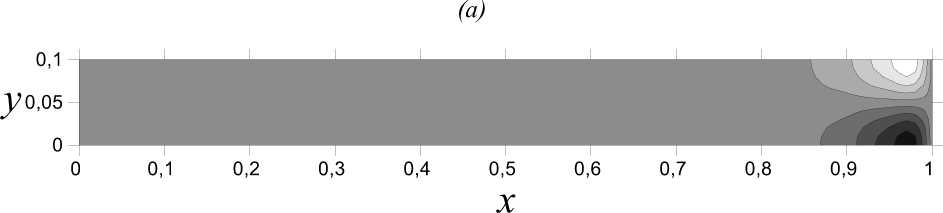
^^■H c,(x,y)-10I

-2,2   -1,7   -1,2   -0,7   -0,2    0,3    0,8    1,3    1,8

(б)

Рис. 2. Поле возмущения мобильной концентрации q ( x , y ) для параметров

а) % = 1, Pe = 1 , б) % = 1, Pe = 10

-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9

pfx.yylO2

(а)

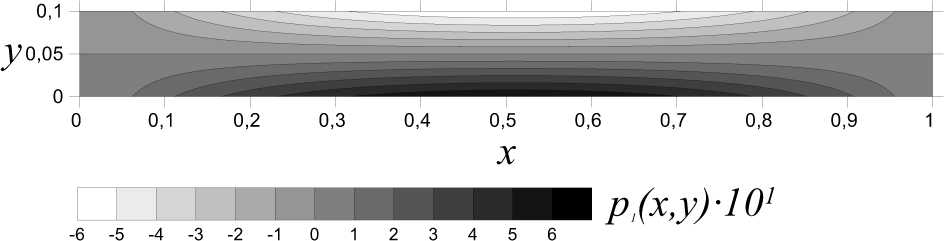
(б)

Рис. 3. Поле возмущения давления p_x ( x , у ) для параметров а) % = 1, Pe = 1 ,

б) % = 1, Pe = 10

Показано, что поле концентрации в первом порядке малости представляет собой конвективную ячейку, таким образом возникают области с повышенной и пониженной концентрацией примеси. Также видно, что с увеличением числа Пекле течение стабилизируется, снижается интенсивность конвекции. Наблюдаемое смещение ячейки с ростом числа Пекле связано с тем, что в области организуются две ячейки (см. [10] рис. 2а) одна из которых сильно вытянута, и, как следствие, интенсивность возмущения такой ячейки значительно ниже. Увеличение числа Пекле приводит к тому, что левая ячейка вытягивается, а правая сжимается у выхода из области. Смена интенсивности ячеек приводит к тому, что области пониженной и повышенной концентрации на входе с ростом числа Пекле меняются местами на выходе из рабочей области. Качественно результаты аналитического расчета полученная структура возмущений и их локализация совпадают с результатами численного счета, описанного в работе [10]. Разница же в количественном описании связана с тем, что для построения аналитических результатов зависимость от времени не учитывается, так как полученное решение рассматривается в пределе больших времен, при которых распределение давления и концентрации являются стационарными.

Решена задача об устойчивости одномерного течения в прямоугольной области пористой среды в присутствии горизонтального перепада давления и концентрации. При малых значениях числа Рэлея–Дарси получены аналитические выражения для полей возмущений давления и концентрации. Показано, что результат численного и аналитического расчета качественно совпадают. Результаты численного и аналитического расчетов показывают, что в случае непроницаемых горизонтальных границ установившееся течение для бесконвективного случая является неустойчивым даже при малых числах Рэлея–Дарси.

• 1.    Schincariol, R. A. and Schwartz, F. W. (1990), "An experimental investigation of variable density flow and mixing in homogeneous and heterogeneous media", Water Resources Research , vol. 26, no. 10, pp. 2317-2329.

• 2.    Maryshev, B. S., Khabin, M. R. and Evgrafova, A. V. (2023), "Identification of transport parameters for the solute filtration through porous media with clogging", Journal of Porous Media, vol. 26, no. 6, pp. 31-35.

• 3.    Deans, H. A. (1963), "A mathematical model for dispersion in the direction of flow in porous media", Society of Petroleum Engineers Journal, vol. 3, no. 01, pp. 49-52.

• 4.    van Genuchten, M. T. and Wierenga, P. J. (1976), "Mass transfer studies in sorbing porous media I. Analytical solutions 1", Soil Science Society of America Journal, vol. 40, no. 4, pp. 473-480.

• 5.    Schumer, R., Benson D. A., Meerschaert M. M. and Baeumer, B. (2003), "Fractal mo-bile/immobile solute transport", Water Resources Research, vol. 39, no. 10.

• 6.    Gouze P., Le Borgne, T., Leprovost, R., Lods, G., Poidras, T. and Pezard, P. (2008), "Non-Fickian dispersion in porous media: 1. Multiscale measurements using single-well injection withdrawal tracer tests", Water Resources Research, vol. 44, no. 6, W06426.

• 7.    Selim, H. M. (1989), "Prediction of contaminant retention and transport in soils using kinetic multireaction models", Environmental Health Perspectives, vol. 83, pp. 69-75.

• 8.    Nield, D. and Bejan, A. (2017), "Convection in Porous Media", Cham, Switzerland: Springer , 988 p.

• 9.    Naifeh, A. (1984), "Introduction to methods of perturbations", Moscow: Nauka , 535 p. (In Russ.).

• 10.    Khabin, M. R. and Maryshev, B. S. (2023), "The onset of concentration convection in a long rectangular domain of a porous medium", Bulletin of Perm University. Physics, no.4, pp. 10-23. (In Russ.).