Применение метода наибольших вкладов в технике инверсии магнитограмм

Сферические гармонические функции были впервые использованы для аналитического представления магнитного поля Земли почти два века назад [Gauss, 1839]. Созданный Карлом Гауссом сферический гармонический анализ (СГА) получил развитие в классических работах [Schuster, Lamb, 1889; Schmidt, 1935; Chapman, Bartels, 1940] и стал в дальнейшем основным методом как для разработки моделей главного магнитного поля, так и для расчета внутренних и внешних источников (эквивалентных токов) спокойных геомагнитных вариаций (суточных и сезонных) в средних и низких широтах в рамках двумерной ионосферной динамо-теории [Бенькова, 1941; Fougere, 1963; Мишин, 1976; Яновский, 1978; Haines, Torta, 1994; Backus et al., 1996; Mandea, Korte, 2010; Olsen et al., 2010].

В ИСЗФ СО РАН метод СГА для переменного геомагнитного поля в динамо-области, а главное — в высокоширотной области полярной ионосферы, стал активно развиваться под руководством В.М. Мишина с момента основания Института в 1960 г. [Мишин, Базаржапов, 1966; Базаржапов и др., 1966, 1979; Шпынев и др., 1974; Мишин, 1976; Мишин и др., 1982, 1984; Ширапов и др., 2000] . В настоящее время СГА остается основным блоком программного комплекса техники инверсии магнитограмм (ТИМ) [Базаржапов и др., 1979; Mishin, 1990; Ширапов, Мишин, 2009] — оригинального метода, позволяющего рассчитывать ионосферные источники (электрические поля и токи) наземных геомагнитных вариаций по данным их измерений на мировой сети магнитных станций.

Методом СГА решается обратная задача теории потенциала для квазистационарного гармонического геомагнитного поля в приземном слое непроводящей атмосферы [Chapman, Bartels, 1940; Яновский, 1978] . Из уравнения Лапласа для скалярного магнитного потенциала и свойства потенциальности геомагнитного поля следует система линейных алгебраических уравнений (СЛАУ), которая в ТИМ [Базаржапов и др., 1979] имеет вид

ЕЕ (gm cosm1+hm sinmx)dP(cos9) = X, n=1 m=0

N                         \mP m ( cos 9 )

i EE ( g m sin ^{m 1-} h m cos^{m x} ) —• _Q    = Y , ⁽¹⁾

n=1 m VSin

NUnu,

EE( j cos m1 + kn sin m XP (cos 9)

n = 1 m = 0

где X , Y , Z — компоненты вариаций геомагнитного поля в дипольной системе координат, измеренные на станциях-магнитометрах; θ — дипольная коши-рота; λ — местное геомагнитное время;

m mm   m mmmm    m gn    En + In ;      hn    en + in ; jn    nEn   (n + 1) In ;

km = nem -(n +1) im; Em , em, I’m , im — сфериче ские коэффициенты; P™ (cos 9)

d P m ( cos 9 ) и

d9

присоединенные полиномы Лежандра степени n и порядка m , заданные в нормировке Шмидта, и их производные [Schmidt, 1935] .

В системе (1) количество столбцов равно количеству неизвестных и зависит от N, а количество строк равно 3K, где K — количество наземных магнитометров. С одной стороны, при выборе N необходимо учитывать K так, чтобы количество неизвестных не превышало количество уравнений. С другой стороны, при использовании лишь части первых столбцов, отсекается остальная часть спектра, которая в общем случае могла бы лучше аппроксимировать исходное поле, заданное на неоднородной сети. Таким образом, возникает задача выбора из ряда сферических функций такого конечного подмноже- ства, которое с приемлемой точностью аппроксимирует ПГВ — задача выбора оптимального спектра аппроксимирующих функций.

По полученным для системы (1) коэффициентам СГА рассчитывается внешняя и внутренняя токовые функции, ответственные за ПГВ, наблюдаемое на поверхности Земли. Формула расчета внешней эквивалентной токовой функции по коэффициентам СГА J (θ, λ) имеет вид [Chapman, Bartels, 1940; Базаржапов и др., 1979; Haines, Torta, 1994]

2 n + 1 1 r | n + 1 I R J

E

N

J ( 9 , 1 ) = - R E- £

Ц ) n = 1

X

N x£ (Em cosm 1 + em sinmX)P,m (cos 9), m=0

где μ₀ = 4π·10^–7 Гн/м — магнитная постоянная; r = R _E + h ; R _E = 6371 км — радиус Земли; h = 115 км — приведенная высота токонесущего слоя ионосферы.

В программном комплексе ТИМ сферические коэффициенты системы (1) и внешняя эквивалентная токовая функция (2) составляют основу расчетов пространственных распределений важнейших электродинамических параметров полярной ионосферы и магнитосферы в двух полушариях (границы авроральных овалов, интегральные проводимости, горизонтальные электрические поля и токи, продольные токи (ПТ) и другие параметры) [Базаржапов и др., 1979; Mishin, 1990; Лунюшкин, Пенских, 2019] .

Количество строк системы (1) зависит от числа работающих станций-магнитометров, а количество столбцов — от используемого спектра степени n и порядка m [Базаржапов и др., 1966; Мишин и др., 1984]. Таким образом, система может быть как переопределенной, так и недоопределенной. При m=0 появляются нулевые столбцы, а для Y-компоненты в системе (1) также появляются нулевые подстроки. В случае плохой обусловленности системы малые изменения X-, Y-, Z-компонент приводят к значительным изменениям искомых коэффициентов [Тихонов, Арсенин, 1979]. Как следствие, источники поля геомагнитных вариаций (ПГВ) для двух последовательных моментов времени с практически одинаковыми вариациями аппроксимируются значительно отличающимися коэффициентами, что противоречит и логике, и реальным наблюдениям. Наличие неизбежной погрешности магнитометров, измеряющих магнитное поле Земли, а также выбор способа определения уровня отсчета ПГВ [Gjerloev, 2012] влекут также неустойчивость решения СЛАУ (1) [Мишин и др., 1982]. Существует ряд методов решения систем линейных уравнений [Фаддеев, Фаддеева, 1963]. С учетом особенностей глобальных распределений магнитных данных в ТИМ для решения СЛАУ был разработан метод наибольших вкладов (МНВ), который показал высокую надежность и эффективность [Шпынев и др., 1974; Базаржапов и др., 1979]. МНВ работает на основе мгновенных данных ПГВ, заданных на неоднородно распределенной сети наземных магнитометров. Это усложняет решение обратной задачи [Sneeuw, 1994], но позволяет получить 1-минутные мгновенные экви- валентные токовые функции без всяких усреднений по времени. Большинство других существующих методов СГА в отличие от МНВ требуют однородного распределения исходных данных на сфере [Barraclough, 1978].

Наземные магнитометры сосредоточены преимущественно в Северном полушарии, поэтому несколько десятков лет задача ТИМ с помощью МНВ успешно решалась только для одного полушария. Благодаря проекту SuperMAG увеличилось количество доступных данных мировых наземных магнитометров, включая Южное полушарие [Gjerloev, 2012] . Это сделало возможным проведение расчетов не только для Северного, но и для Южного полушария, а также послужило одной из причин создания нового программного комплекса ТИМ.

Цели настоящей работы: описать современное состояние МНВ как одного из важных элементов ТИМ, с помощью которого уже получены первые непротиворечащие научные результаты для двух полушарий Земли одновременно [Lunyushkin et al., 2019] ; провести специальное сравнение МНВ с двумя другими популярными методами, применяемыми для решения систем уравнений аналогичных геофизических задач.

1. ОСНОВЫ МЕТОДА НАИБОЛЬШИХ ВКЛАДОВ

В случае однородной сети исходных данных ПГВ раскладывается по системе ортогональных сферических функций, которую можно рассматривать как систему ортогональных векторов, т. е. ортогональный базис. В случае неоднородной сети система векторов является неортогональной.

В матричном виде СЛАУ выражается уравнением:

Ax=b , (3) где A — матрица коэффициентов, b — вектор-столбец свободных членов, x — вектор-столбец неизвестных. В общем случае матрица A может быть неквадратной.

Введем обозначения: C = cos( m λ), S = sin( m λ). Для наглядности используем одну станцию-магнитометр и зафиксируем n и m , тогда СЛАУ (1) можно представить в виде (3), где

рицы x . Таким образом, в общем случае система (1) может оказаться как недоопределенной, так и переопределенной. Путем выполнения последовательных итераций МНВ позволяет получить приближенное решение такой системы независимо от ее размерности.

Рассмотрим основные моменты метода наибольших вкладов на упрощенном примере СЛАУ с двумя уравнениями и двумя неизвестными

Г a 11 x 1 + a ₁₂ x 2 = b 1 ,

I a 21 ^X 1 ⁺ a 22 x 2 = b 2 ^.

Матрицу можно рассматривать как совокупность столбцов или совокупность строк [Беклемишев, 1998] . Если разбить матрицу A на отдельные вектор-столбцы, то СЛАУ можно представить в виде

x ₁

a 11

a 21

+ X 2

a 12

b ₁

b ₂

	" С P. 59	d p- Sn 59	С d p — 59	5 P m Sn 59
A =	„ mP m	mPm	mPm	mPm
	s-^	- С —”—	Smn	- С —”—
	sin 9	sin 9	sin 9	sin 9
	cnP — -	SnP n m	- С ( n + 1 ) P m	- S ( n + 1 ) P —

Эту систему можно представить в виде x ₁ a ₁ + x ₂ a ₂ = b ,                                  (4)

где a 1 = ( a 11 , a 21 ), a 2 = ( a 12 , a 22 ) — новые базисные векторы в двумерном пространстве, x 1 , x 2 — скаляры при базисных векторах, b = ( b 1 , b 2 ) — вектор-результат, который получается путем сложения двух базисных векторов, умноженных на соответствующие скаляры. Векторы b , a 1 , a 2 заданы в ортонорми-рованном базисе e 1 , e 2 .

Таким образом, решение СЛАУ равносильно разложению заданного вектора b по заданному базису a 1 , a ₂, т. е. поиску такого вектора x , компоненты которого являются координатами вектора b в базисе a 1 , a 2 .

Уравнение (4) можно представить в виде x1a1 + x2a2 = b1e1 + b2e2.                        (5)

Таким образом, из (4) следует: ( b 1 , b 2 ) — координаты вектора b в исходном ортонормированном базисе e ₁, e ₂; ( x ₁, x ₂) — координаты вектора b в новом базисе a ₁, a ₂; ( a ₁₁, a ₂₁), ( a ₁₂, a ₂₂) — координаты векторов a ₁, a ₂ в базисе e ₁, e ₂.

Из курса линейной алгебры известно, что для разложения вектора по новому базису необходимо решить СЛАУ [Беклемишев, 1998] . Однако можно поставить обратную задачу — решить СЛАУ путем разложения вектора в новом базисе.

Обозначим proj ab скалярную проекцию вектора на вектор, projab — векторную проекцию вектора на вектор.

b • a proj ^ab = H

Если количество пунктов наблюдений равно K , система (1) будет состоять из 3 K таких подсистем. При увеличении n и m увеличивается количество столбцов матрицы A , а также количество строк мат-

b • a projab =     a , a • a где b • a — скалярное произведение векторов b и a, b • a a — евклидова норма вектора a. Величина

a отражает длину проекции в единицах длин вектора e (исходного базисного вектора).

Величина —a отражает длину проекции в еди- a • a ницах длин вектора a (нового базисного вектора).

Очевидно, что ||b - proj_ab|| <  ||b| |.

Рассмотрим задачу поиска приближенного решения СЛАУ. Такая задача возникает в случае отсутствия точного решения, плохой обусловленности СЛАУ, лимита времени на решение СЛАУ, необходимости нахождения переменных, оказывающих наибольшее влияние на решение СЛАУ и др. Именно такая задача и стоит в ТИМ: необходимо выбрать из матрицы A такие столбцы, такой спектр аппроксимирующих функций, который наилучшим образом аппроксимировал ПГВ.

Решение СЛАУ (3) можно найти путем последовательного вычитания из вектора b его проекций на базисные вектора, которые содержит матрица A . Однако для обеспечения наиболее быстрой сходимости следует вычитать ту проекцию, которая максимально уменьшит норму. Для этого необходимо вычитать проекцию не на произвольный вектор, а на тот, модуль проекции на который максимален, поскольку, чем больше вычитаемая проекция, тем меньше невязка. Следуя данному принципу на каждом этапе, получаем следующий алгоритм решения СЛАУ (3):

тирующий базис, поскольку базисные векторы при нулевых элементах вектора x в формировании вектора b фактически не участвуют.

В результате работы описанного алгоритма определяется такое подмножество базисных векторов матрицы A , которое оптимальным образом аппроксимирует вектор b . В системе уравнений (1) ТИМ матрица A содержит сферические функции, а вектор b — ПГВ, заданное на неоднородной либо однородной сети магнитных станций. Таким образом, суть МНВ состоит в аппроксимации поля (в нашем случае ПГВ) с помощью оптимального подмножества сферических гармоник.

1. t = 0, b ₀ = b , x ₀ = 0

2. ПАРАМЕТР РЕЛАКСАЦИИ В МЕТОДЕ НАИБОЛЬШИХ ВКЛАДОВ

Выше указывалось на необходимость вычитания максимальной проекции, но в ряде случаев не получается выделить одну такую проекцию — пример дан на рис. 1. Модули проекций на базисные векторы в данном примере одинаковые, выбирается первая из максимальных проекций.

На крайне упрощенном примере решения СЛАУ

2. do

( a )

m = argmax

(| proj « j b| )

A =

, b =

x =

3/7

3/7

( b )

( c )

( d )

proj _a b _t

m t+1 t         «a mil bt+1 = bt — Projam bt t = t + 1

e _m

3. while ( t <  MAXT )

and (|b _t ||> NORM )

видно (рис. 2), что при вычитании всей проекции (ξ = 1.0) решение сходится неравномерно, и, если прервать решение по истечении лимита на количество итераций, окажется, что x 1 ≠ x 2 . Для более равномерной сходимости на каждой итерации можно вычитать не всю проекцию, а ее часть (ξ ≠ 1.0).

Покажем справедливость такого подхода. Рассмотрим произвольный вектор v как сумму двух векторов

Здесь t — номер итерации; m — номер базисного вектора-столбца, на который будет осуществляться проекция; b _t — вектор невязки на t -й итерации; x _t — вектор корней СЛАУ на t -й итерации; MAX_T — максимально допустимое количество итераций; NORM — норма, при которой решение должно быть остановлено.

Максимальная проекция вектора на базисный вектор определяется в виде

maxProj = max

(| proj a^) ,

v = ξ v +(1 – ξ) v                            (6)

где 0 <  ^ <  1.

Рассмотрим пункт ( c ) алгоритма:

b t +1 = b t – proja _m b t .

Поскольку projambt является вектором, то, используя (6), получим b t+1 = b t - ^PrOjam Ь t -(1 - ^ ) prOjam Ь t,

m = argmax

(| proj «?|) ,

где argmax() — функция, возвращающая индекс максимального элемента в массиве; max() — функция, возвращающая значение максимального элемента в массиве.

В качестве аргумента функции в argmax() и max() передается массив модулей проекций b на каждый a j -й базисный вектор.

На первой итерации алгоритма вектор x содержит только нулевые элементы, к окончанию алгоритма вектор x содержит как нулевые, так и ненулевые элементы. Базисные векторы матрицы A при ненулевых элементах вектора x составляют резуль-

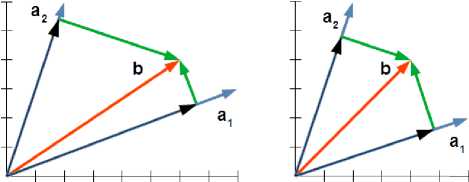
Рис. 1. Выбор базисного вектора с максимальной проекцией. Слева — простой выбор, максимальная проекция вектора b будет на вектор a ₁, справа — неоднозначный выбор, поскольку проекции вектора b на векторы a ₁, a ₂ одинаковы по модулю; b (красный) — исходный вектор; a ₁, a ₂ (синие) — базисные векторы, на которые производится проекция; черные — проекции вектора b на векторы a ₁, a ₂ соответственно

b t + 1 + ( 1 - ^ ) Proj a m b t = b t - ^ Proj a m b t .

Таким образом, в процессе решения вычитается не вся проекция, а ее часть (рис. 2). Часть проекции остается в векторе невязки. Тем не менее, невязка по-прежнему будет снижаться на каждой итерации. Легко заметить (рис. 2, 3), что невязка будет устойчиво снижаться при значениях 0 <  £ <  2 .

Тогда пункты (b), (c) алгоритма можно переписать в виде proja bt

• ⁽ b )    x t + i = x t ⁺ ^       m e m ,

^a m

• ⁽ c )    ^b t + i = ^b t - ^ Proj a m ^b t .

Алгоритм с вышеизложенными изменениями применительно к задаче ТИМ является оригинальным МНВ. В исходном коде ранее созданной оригинальной программы МНВ был задан постоянный параметр ξ=0.7. Кроме того, в качестве дополнительного критерия остановки алгоритма оценивается не только норма невязки, но и изменение нормы невязки. В основе МНВ лежит неполная релаксация по длине вектора невязки [Фаддеев, Фаддеева, 1963] .

Стоит отметить, что введение параметра ξ при решении СЛАУ с ортогональным базисом приведет лишь к увеличению количества итераций. Использование параметра 0 <  ^ <  1 может быть оправданным в случае неортогонального и/или избыточного базиса. В таком случае у других базисных векторов повышается шанс оказаться в итоговом базисе. Использование параметра 1 <  ^ <  2 может быть оправданным при решении плохо обусловленных СЛАУ. Параметр релаксации ^ * 1.0 может уменьшить количество итераций, достаточных для решения СЛАУ. Стоит учесть, что слишком малые значения ξ, наоборот, приведут к увеличению количества итераций. Влияние параметра ξ можно сравнить с коэффициентом обучения, который определяет длину шага в методе градиентного спуска, x _{t + 1} = x _t - ^ V F . Алгоритмами поиска оптимального значения коэффициента обучения занимаются многие ученые, однако эта задача до сих пор окончательно не решена. Коэффициент обучения в методе градиентного спуска и параметр релаксации в МНВ имеют схожий математический смысл, поэтому для МНВ можно использовать уже известные способы оптимизации сходимости [Jacobs, 1988] .

Рассмотрим пункты (b), (c) алгоритма. Математически на любой итерации должно выполняться равенство bt+1 - bo - Axt+1.                                      (7)

Однако выполнение пункта ( c ) из-за вычислительных погрешностей, обусловленных арифметикой с плавающей запятой [Goldberg, 1991] , приводит к нарушению равенства (7), что может дать значительные ошибки округления при большом количестве итераций. Эту проблему можно разрешить двумя способами.

Первый способ — замена пункта ( c ) и явный пересчет невязки на каждой итерации:

b t + 1 = b o — Ax t + 1 .                                      (8)

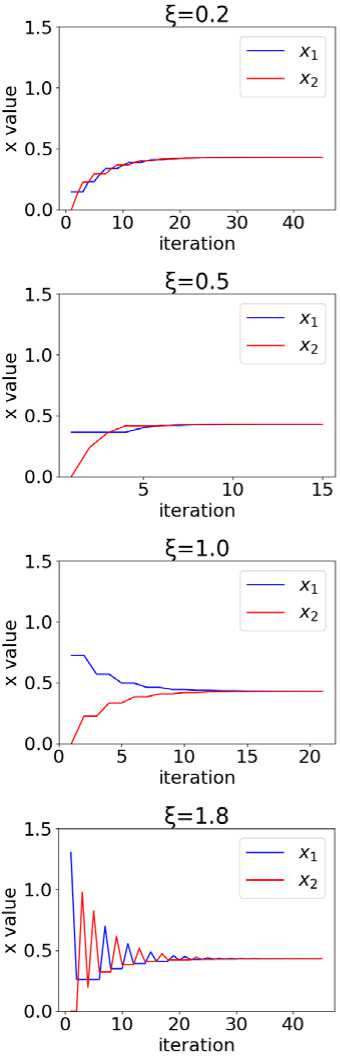
Рис. 2 . Ход решения при различных параметрах релаксации. Ось абсцисс — номер итерации, ось ординат — значение переменной, синий — переменная x ₁, красный — переменная x ₂

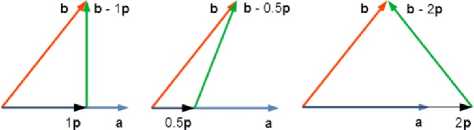
Рис. 3. Слева (ξ=1.0) — вычитание проекции вектора; в центре (ξ=0.5) — вычитание половины проекции вектора; справа (ξ=2.0) — вычитание двух проекций вектора: b (красный) — исходный вектор, a (синий) — вектор, на который производится проекция; ξ p (черный) — проекция вектора на вектор, умноженная на соответствующий параметр релаксации; зеленый — отклонение от проекции вектора на вектор, умноженной на соответствующий параметр релаксации

Второй способ — использование алгоритмов компенсирующего сложения [Kahan, 1965; Klein, 2006] .

Стоит отменить, что оба способа повышают численную устойчивость метода, но снижают скорость его работы. Формулы (7), (8) показаны для ξ=1, но, очевидно, что их легко модифицировать и для других значений ξ.

• 3.  СРАВНЕНИЕ МЕТОДОВРЕШЕНИЯ ОСНОВНОЙ СИСТЕМЫ УРАВНЕНИЙВ ТЕХНИКЕ ИНВЕРСИИ МАГНИТОГРАММ

  Для решения неопределенных СЛАУ существуют различные методы, каждый из которых имеет свои достоинства и недостатки. Наиболее известным и часто используемым является метод наименьших квадратов (МНК) (ordinary least squares, OLS), который широко используется и в геофизике [Rangarajan, Rao, 1975; Weimer, 1995] .

Решение СЛАУ с помощью МНК можно представить в виде

Ax = b ,

ATAx = ATb, x = (ATA) ATb.

В ТИМ матрица A ^T A является плохо обусловленной (число обусловленности ~10²⁰), поэтому математически точное решение СЛАУ является неверным, следовательно, необходимо найти менее точное, но более стабильное решение. Для этого при решении СЛАУ дополнительно к МНК используем стабилизированный метод бисопряженных градиентов (BiCGStab), поскольку он позволяет прервать вычисление на любой итерации, не дожидаясь точного решения.

Другой популярный в геофизике метод решения неопределенных СЛАУ основан на сингулярном разложении матрицы A (singular value decomposition, SVD) [Pulkkinen et al., 2003] . В этом методе рассчитывается псевдообратная матрица A ⁺, по которой находится решение СЛАУ.

A = ULV ^T ,

A+ = VL+UT, x = A+b.

Выполнение одной итерации BiCGStab изменяет все элементы вектора x , поэтому выделить отдельные столбцы (оптимальный спектр) не удается. Это относится и к SVD — в матрице A не будет нулевых столбцов, даже если занулить все сингулярные числа кроме первого. Следовательно, не будет и нулевых значений координат вектора x . Таким образом, SVD и BiCGStab не позволяют выбрать подмножество столбцов СЛАУ (оптимальный спектр аппроксимации), как это делает МНВ.

Сравним методы решения обратной задачи на примере хорошо изученной изолированной суббури 27.08.2001 [Mishin et al., 2017] . Решим систему (1)

методом МНВ и двумя вышеуказанными методами для момента 03:55 UT предварительной фазы указанной суббури. Поскольку на подготовительной фазе суббури имеет место плавное усиление стационарной магнитосферной конвекции, эквивалентный ток Холла (аналог ионосферной конвекции) [Лунюш-кин, Пенских, 2019] должен отражать классическую ровную двухвихревую систему магнитосферноионосферной конвекции.

На рис. 4 представлены эквивалентные токовые функции для Северного и Южного полушарий, рассчитанные для выбранного события тремя разными методами. Видно, что в Северном полушарии все методы в целом дают схожие по структуре эквивалентные токовые функции, но в приполюсной области методы МНК и SVD показывают мелкомасштабные изменения двухвихревой системы конвекции. В Южном полушарии ожидаемую (симметричную) двухвихревую систему ионосферной конвекции удалось получить только с помощью МНВ. Одной из характеристик токовой функции является трансполярный ток, отражающий интенсивность ионосферной конвекции через полярную шапку [Базаржапов и др., 1979; Lunyushkin et al., 2019] . В таблице на основе рис. 4 для каждого метода представлены значения токовой функции в двух основных фокусах, трансполярный ток, а также межполушарное соотношение трансполярных токов.

Магнитосферные и авроральные суббури происходят в двух полушариях одновременно [Akasofu, 1977] . Двухвихревая система ионосферных токов, величина ПГВ для двух полушарий в целом должны быть одинаковы, поскольку они в равной степени зависят как от внешних параметров солнечного ветра и ММП, так и от внутренних магнитосферных процессов. На межполушарную асимметрию в первую очередь влияет угол наклона геомагнитного диполя. При большом угле одно из полушарий оказывается более освещенным Солнцем, что увеличивает проводимость ионосферы и, как следствие, ионосферный ток.

Угол наклона диполя для 27.08.2001 03:55 UT равен 0.24°, поэтому освещенность и создаваемая ею волновая проводимость в Северном и Южном полушариях в дипольной системе координат практически одинаковы. Следовательно, эквивалентные токовые функции и трансполярный ток Северного и Южного полушарий также должны быть практически одинаковы. Как видно из таблицы, это условие выполняется для МНВ, но не выполняется для двух других методов. Эквивалентные токовые функции двух полушарий, полученные с помощью МНВ, в целом являются подобными, а отношение трансполярных токов составляет 0.94, т. е. близко к 1. Напротив, для двух других методов эквивалентные токовые функции Северного и Южного полушарий значительно отличаются друг от друга, а трансполярный ток Северного полушария превышает трансполярный ток Южного полушария более чем в два раза.

Из-за близкого к нулю угла наклона диполя должно также наблюдаться межполушарное подобие продольных токов и их границ. На рис. 5 представлены продольные токи при однородной проводимости с границами, полученными автоматическим

Сравнение трансполярных токов двух полушарий

	North, kA			South, kA			I tr,N /I tr,S
	min	max	I tr	min	max	I tr
MMC	–90	170	260	–109	168	277	0.94
OLS+BiCGStab	–122	168	290	–56	58	114	2.54
SVD	–95	132	227	–60	43	103	2.20

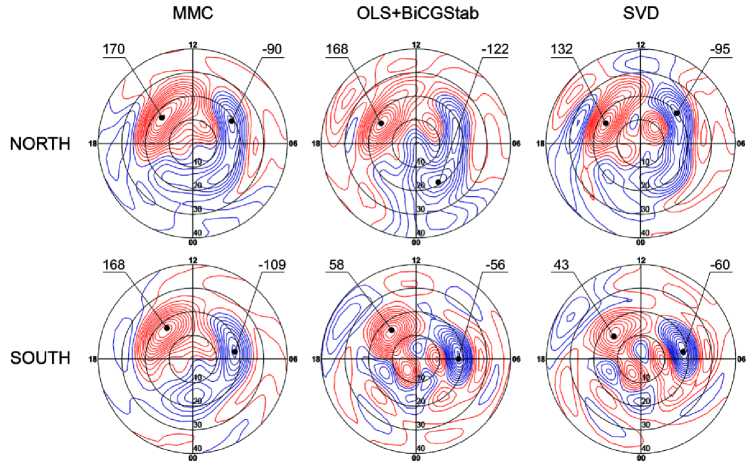
Рис. 4. Сравнение результатов численных методов решения уравнения (1) на примере эквивалентных токовых функций, рассчитанных для момента 03:55 UT изолированной суббури 27.08.2001. Верхний ряд — токовые функции в Северном полушарии, нижний ряд — в Южном. Первый столбец — результаты работы МНВ (MMC — method of maximum contribution), второй — МНК (OLS — ordinary least squares) со стабилизированным методом бисопряженных градиентов (BiCGStab), третий — сингулярного разложения (SVD). Выносными линиями показаны значения токовой функции в главных фокусах (в килоамперах)

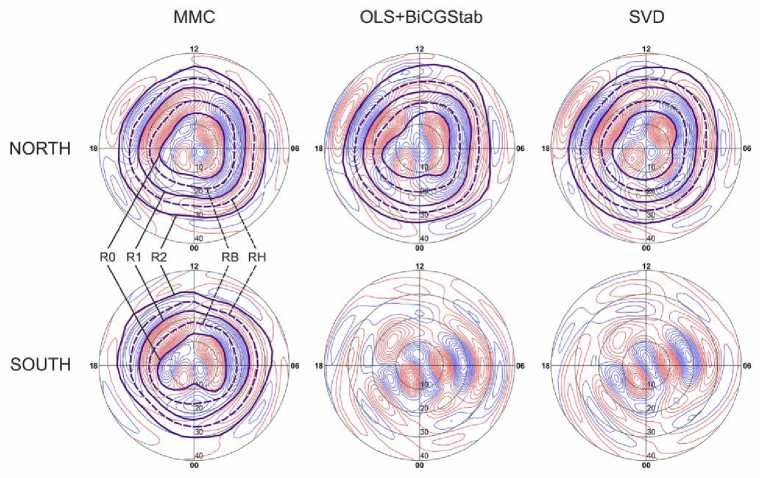
Рис. 5. Сравнение результатов численных методов решения уравнения (1) на примере продольных токов при однородной проводимости, рассчитанных для момента 03:55 UT изолированной суббури 27.08.2001. Верхний ряд — продольные токи в Северном полушарии, нижний ряд — в Южном. Первый столбец — результаты работы МНВ (MMC — method of maximum contribution), второй — МНК (OLS — ordinary least squares) со стабилизированным методом бисо-пряженных градиентов (BiCGStab), третий — сингулярного разложения (SVD). R0 — граница полярной шапки, RB — граница обращения конвекции (линия максимума продольных токов зоны 1), R1 — граница между зоной 1 и зоной 2 продольных токов, RH — линия максимума продольных токов зоны 2, R2 — экваториальная граница аврорального овала методом [Лунюшкин, Пенских, 2019]. Продольные токи двух полушарий, полученные с помощью МНВ, в целом являются подобными, подобны также и границы ПТ. Этого не удалось получить методами МНК и SVD, поскольку распределения ПТ Северного и Южного полушарий значительно различаются, а выделить зоны ПТ практически невозможно.

Таким образом, можно сделать вывод, что решение, полученное с помощью МНВ, оказалось лучшим из трех рассмотренных методов.

ЗАКЛЮЧЕНИЕ

В работе дано подробное описание оригинального МНВ, используемого в ТИМ. Продемонстрирована работа параметра релаксации ξ в МНВ и показано, что алгоритм стабильно сходится при значении параметра релаксации 0 < ^ <  2. Влияние параметра релаксации ξ в МНВ имеет сходство с коэффициентом обучения в методах градиентного спуска, что делает возможным применение известных алгоритмов для оптимизации. Предложены модификации оригинального метода МНВ, повышающие точность и/или скорость решения СЛАУ.

Для задачи ТИМ проведено сравнение методов МНВ, OLS+BiCGStab и SVD. МНВ показал наиболее правдоподобный результат, особенно для Южного полушария. Расчеты на основе МНВ также подтверждают ожидаемую межполушарную симметрию эквивалентных токовых функций, трансполярных токов, распределений продольных токов и их границ.

Автор выражает признательность создателям оригинального метода наибольших вкладов В.М. Мишину, Г.Б. Шпыневу, А.Д. Базаржапову и Д.Ш. Ширапову. Автор благодарит С.Б. Лунюшкина за поставленную задачу и плодотворные дискуссии, а также В.В. Мишина и А.В. Тащилина — за полезные замечания.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-3590046.

Организации и сотрудники, которым автор выражает глубокую признательность за возможность использования данных наземных магнитометров: Мировая сеть магнитных обсерваторий ИНТЕР-МАГНЕТ; Дж. Дж. Лав (Геологическая служба США, USGS); Я. Манн (CARISMA); CANMOS; К. Юмото и К. Шиокава (база данных S-RAMP); база данных SPIDR; О. Трошичев (AARI); М. Энгебретсон (программа MACCS); отдел геомагнетизма Геологической службы Канады; GIMA; MEASURE, UCLA IGPP и Флоридский технологический институт; Е. Зеста (SAMBA); К. Юмото (Chain 210); Ф. Онари (SAMNET); Э. Тансканен (институты, которые поддерживают сеть магнитометров IMAGE); PENGUIN; М. Коннорс (AUTUMN); Р. Бельке (DTU Space); Л.Дж. Ланцаротти и А.Т. Везервакс (магнитометр МакМердо); ICESTAR; RAPIDMAG; Британская антарктическая служба; P. Чи (McMac); С. Макмиллан (BGS); Институт земного магнетизма, ионосферы и распространения радиоволн им. Пушкова (ИЗМИРАН); Дж. Мацка (GFZ); Б. Хейлиг

(MFGI); Дж. Реда (IGFPAS); М. Велланте (Университет Аквилы); В. Лесур и А. Чембодат (BCMT); М. Костелло (данные получены в сотрудничестве с Австралийским агентством по наукам о Земле); Дж.В. Гьер-лоев (SuperMAG). Данные, использованные в настоящем исследовании, доступны на сайте SuperMAG [].