Применение метода наложенных сеток для численного решения задач сейсмики сеточно-характеристическим методом

Одним из способов изучения строения и свойств геологических структур является вычислительный эксперимент. Он опирается на. моделирование распространения упругих волн в среде. Для исследования необходимо точно и подробно описывать строение таких структур с учетом формы границ и глубинных неоднородностей [11]. Среди прочего, неотъемлемой частью моделирования реалистичных геологических структур является учет особенностей рельефа: возвышенностей, ущелий, каньонов и т.д. К неоднородностям под поверхностью относятся, к примеру, трещины и полости. Для описания рельефа и неоднородностей в большинстве работ прибегают к использованию неструктурированных вычислительных

«Московский физико-технический институт (национальный исследовательский университет)», 2023

сеток. Этот метод действительно позволяет описать геологическую структуру, однако имеет существенные недостатки. Неструктурированные сетки накладывают ограничения на используемые вычислительные методы, а с ростом моделируемой области и количества неоднородностей в ней растет также и сложность построения неструктурированной расчетной сетки [1, 14]. В случае вычислительных методов, опирающихся на использование структурированных расчетных сеток, моделирование этих особенностей также может быть произведено, однако при их использовании поверхности рельефа или неоднородностей в расчетной сетке будут представлять собой совокупность множества поверхностей, параллельных осям сеток. В данной работе рассматривается применение метода наложенных сеток (он же метод химерных сеток) для моделирования распространения упругих волн в геологической структуре с учетом различных неоднородностей. В качестве численного метода решения возникающей системы дифференциальных уравнений используется сеточнохарактеристический метод [13]. Сеточно-характеристический метод применяется для решения достаточно широкого круга задач механики деформируемого твердого тела [9,11,12]. В данной работе он рассматривается для моделирования динамических пространственных процессов в задачах сейсмики.

2.    Метод наложенных сеток

Метод наложенных сеток позволяет улучшить точность описания рельефа, топографии или локальных неоднородностей внутренней структуры, не требуя при этом перехода к использованию неструктурированной сетки во всей области моделирования. Он широко используется не только в геологии, но и в других задачах моделирования упругого взаимодействия как, например, [8], а также в вычислительной аэро- и гидродинамике [7], где он и был изначально разработан.

При использовании метода наложенных сеток, моделирование среды производится в два этапа. На первом этапе строится регулярная прямоугольная сетка, описывающая физические параметры среды и покрывающая область моделирования с избытком. Эта сетка строится без учета рельефа или неоднородностей. На втором этапе происходит построение дополнительных сеток, каждая из которых частично или полностью описывает поверхность или одну из неоднородностей. Далее можно приступать к моделированию распространения волн. В процессе моделирования на каждом шаге по времени расчет распространения возмущений в каждой из сеток происходит отдельно, а затем перед следующим шагом выполняется синхронизация значений возмущения в сетках посредством интерполяции. Значения в узлах основной сетки, попадающих в покрытую наложенной сеткой область, интерполируются из значений узлов наложенной сетки. К наложенной сетке достраивается по каждой из осей несколько слоев виртуальных узлов, значения в которых интерполируются из узлов основной сетки. Такой подход позволяет обеспечить корректный перенос значений между сетками и избежать ситуаций, когда проинтерполированные значения затем используются для интерполяции в других узлах, приводя к накоплению погрешности. Ранее в [5] был показан пример использования этого метода в двумерном пространстве. Та же идея может использоваться и в трехмерном случае, однако ряд методов и подходов оказываются неприменимыми или требуют учета тех или иных случаев, аналогов которых нет в двумерном случае.

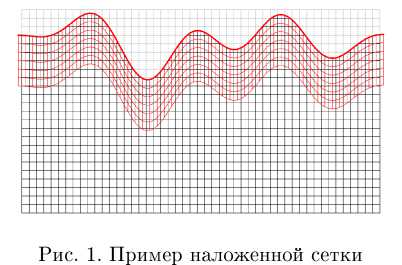
На рис. 1 приведен пример описания двумерной топографии при помощи наложенной сетки. Красным цветом изображена наложенная сетка, жирной красной линией обозначена линия рельефа, описываемая при расчете свободной границей. Основная сетка нарисована черным и серым цветами, серым цветом выделена область над наложенной сеткой, значения в которой не имеют физического смысла и не влияют на расчет.

3.    Проблемы перехода из двумерного пространства в трехмерное

Описание основных проблем интерполяции в трехмерном пространстве удобно проводить путем сравнения двух- и трехмерного случаев. Двумерный случай интереснее одномерного, поскольку в одномерном случае не возникает проблемы поиска соседних точек, все точки могут быть упорядочены по единственной координате, а проверка вхождения точки в интервал тривиальна. У трехмерного случая есть два основных отличия от двумерного.

3.1.    Коллинеарность и комланарность

Если в двумерной сетке провести линии между соседними узлами, то плоскость будет разбита на ячейки-четырехугольники. Мы исходим из предположения, что все эти четырехугольники являются выпуклыми, поскольку сетки, для которых это условие не выполняется, в большинстве случаев являются «плохими» (даже если мы будем корректно обрабатывать их на этапе интерполяции, проблемы возникнут на этапе моделирования). В трехмерном случае все это не так. Интуитивное представление о трехмерной ячейке как об «искаженном кубике» ошибочно, сетки, покрывающие поверхности произвольной формы выглядят иначе. Во-первых, четыре точки, составляющие «грань» ячейки (по аналогии со стороной четырехугольника), в большинстве случаев не компланарны, так что «грань» — это не один четырехугольник, а два треугольника. Во-вторых, требование выпуклости всех ячеек в трехмерии является куда более жестким ограничением, так что его наложение значительно усложняет построение сетки.

3.2.    Разбиение ячейки на симплексы

Если используемый метод интерполяции не предполагает иного, мы представляем значение в точке как взвешенную сумму значений в узлах сетки, образующих ячейку, в которую попадает эта точка. Проверку вхождения точки в ячейку сетки мы выполняем, разбивая ячейку на симплексы и проверяя вхождение в каждый из них. В двумерном случае можно разбить четырехугольную ячейку на два непересекающихся треугольника проведением любой из диагоналей (или какой-то из двух, если снять требование выпуклости). Задача разбиения на симплексы (тетраэдры) в трехмерном случае сложнее.

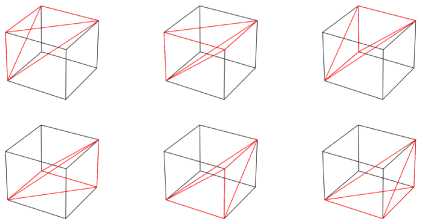
Рис. 2. Иллюстрация разбиения куба на шесть непересекающихся тетраэдров

На рис. 2 представлено возможное разбиение кубической ячейки на тетраэдры. Однако мы имеем дело не с идеальными кубическими ячейками, а с более сложными многогранниками, поэтому использовать такое разбиение не можем. Мы могли бы использовать триангуляцию Делоне, но для наших целей она излишне сложна.

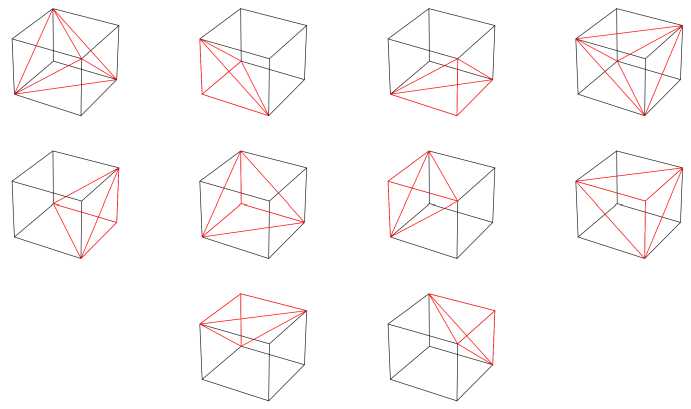
Рис. 3. Иллюстрация используемого разбиения ячейки на тетраэдры

Для простоты реализации мы разбиваем трехмерную ячейку на тетраэдры, не требуя, чтобы они не пересекались, и проверяем большее количество тетраэдров, чем реально необходимо. Если обозначить узлы ячейки ABCDEFGH (пары соседних узлов — АВ₁ ВС, CD, AD, EF, FG, GH, EH, AE, BF, CG, DH\ то тетраэдры, на которые мы разбиваем ячейку: ADBE, BACF, CBDG, DACH, EFHA, FEGB, GFHC, HEGD, ACFH, BDEG (см. рис. 3).

4.    Быстрая проверка точек

Перед тем как пытаться выполнять интерполяцию, имеет смысл выполнять фильтрацию точек, которые нас интересуют, поскольку эта операция «дешевле» с точки зрения затрачиваемых вычислительных ресурсов. Для этого мы используем два подхода — Bounding Box и оболочку множества узлов (необязательно выпуклую).

4.1.    ВВох и Axis-Aligned ВВох

Первый и самый простой способ проверки — это ограничить область пространства, в которой лежат «известные» точки, простым многогранником — прямоугольником или прямоугольным параллелепипедом в дву- и трехмерном случаях соответственно. Если ребра этой ограничивающей фигуры параллельны осям координат, то она называется Axis-Aligned Bounding Box (ААВВ), если нет — просто Bounding Box (ВВ). Можно также потребовать минимальности объема. На практике ААВВ дают большее количество ложноположительных ответов, но их значительно проще строить и несколько проще проверять вхождение, поэтому мы используем их.

4.2.    «Оболочка» сетки

Второй вариант — построение некоторого многогранника, внутрь которого попадут все «известные» точки. Для этого можно использовать, например, выпуклую оболочку. Поскольку мы работаем с сетками, то можем исходить из того, что точки расположены частично упорядоченно, а не произвольным образом, и упростить построение этого многогранника. Сначала мы строим слой виртуальных узлов, координаты которых получаем «продлением линий» между узлами двух крайних слоев сетки (см. рис. 4).

Затем мы говорим, что этот слой узлов задает границу нашей сетки. Если для какой-то точки ближайший узел — виртуальный, то эта точка лежит вне сетки, и пытаться интерполировать в ней мы не будем. Поскольку сетки у нас могут быть закольцованными, то в ряде случаев часть виртуальных узлов не задают границу и должны быть выброшены (см. рис. 5).

Рис. 4. Пример слоев виртуальных узлов (выделены красным) по одной из осей сетки

а)

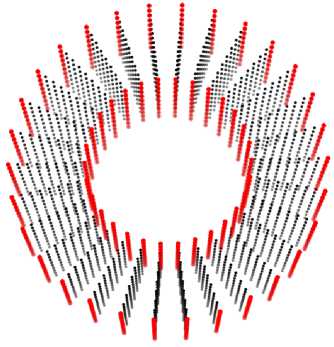
б)

Рис. 5. Пример замкнутой сетки и виртуальных узлов по разным осям: а - виртуальные узлы, не являющиеся частью оболочки сетки из-за ее замкнутости, б - часть оболочки сетки

5.    Используемые методы интерполяции

Нами были реализованы несколько методов интерполяции: метод ближайших соседей, метод естественной окрестности и интерполяция барицентрическими координатами. В этом разделе приведено их краткое описание. Другие методы интерполяции, в частности, би-/трилинейная, би-/трикубическая и сплайны, пока не рассматривались, однако могут быть предметом последующих исследований.

5.1.    Метод ближайших соседей

Интерполяция методом ближайших соседей (kNN) представляет значение в точке в виде взвешенной суммы значений в к ближайших к ней с известными значениями. Предельный случай этого метода — случай к = 1, когда значение приравнивается к значению в ближайшей известной точке. В этом случае фактически происходит разбиение пространства на ячейки Вороного, и в пределах каждой ячейки значения во всех точках полагаются равными значению в точке, которой эта ячейка соответствует.

В случае большего количества точек веса интерполяции определяются взаимным расположением интерполируемой и известных точек. Из принципа чем ближе точки — тем ближе значения следует, что разумно полагать веса суммирования пропорциональными какой-то степенной функции от обратного расстояния. В комбинации с ограничением количества соседей получается модификация метода интерполяции IDW (Inverse Distance

Weighting), впервые предложенного в [6]. Для поиска ближайших соседей мы используем К—d дерево. Идея К—d дерева заключается в разбиении множества точек на подмножества примерно равной мощности по очереди по всем координатам (см. рис. 6).

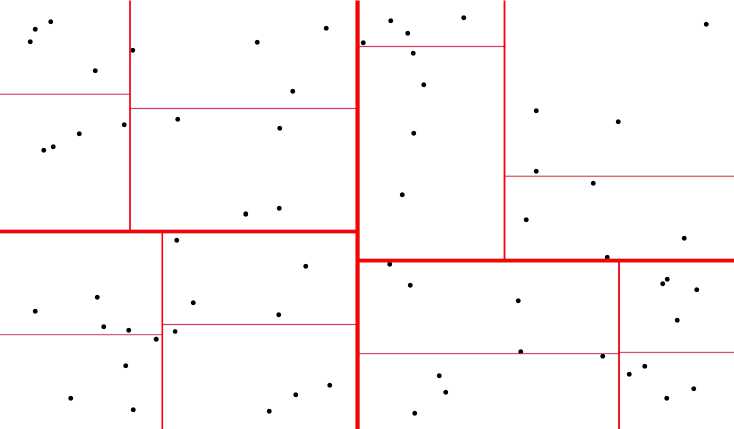
Рис. 6. Иллюстрация К — d дерева в двумерном пространстве. Более поздним разбиениям соответствуют более тонкие линии

Вместо К — d дерева, поиск соседей мы могли осуществлять с помощью R- дерева, но поскольку все точки загружаются в дерево одновременно, их координаты не меняются и все данные помещаются в память, преимуществ у R-дерева в нашем случае нет.

5.2.    Метод естественной окрестности

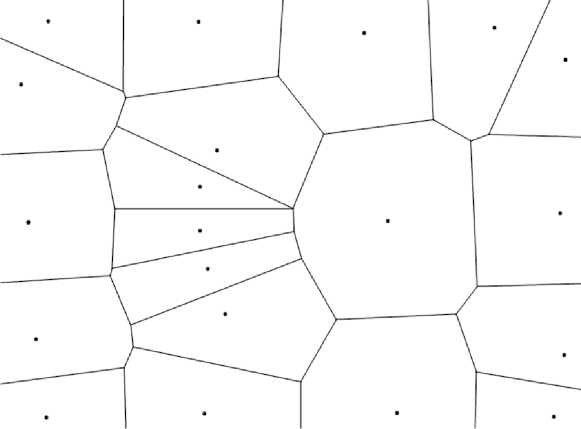
Метод естественной окрестности, также известный как метод похищения площади или метод Сибсона, тоже основан на поиске ближайших соседей точки, однако в отличие от kNN он учитывает не только расстояния, но и взаимное расположение точек. Основой этого метода являются диаграммы Вороного.

а)

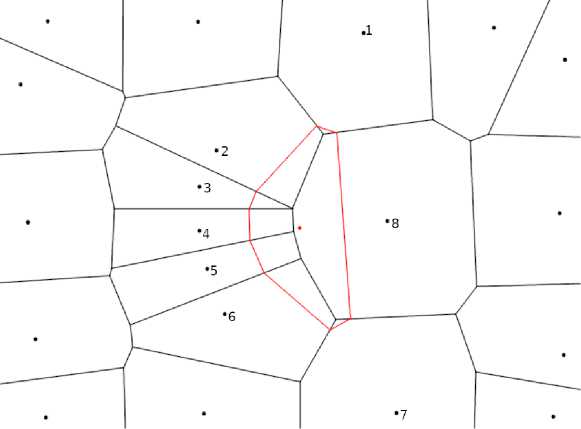
Рис. 7. Диаграммы Вороного в двумерном случае до (а) и после (б) добавления точки

б)

Сначала для точек с известными значениями строится диаграмма Вороного, после чего по очереди для всех точек, значение в которых необходимо проинтерполировать, строятся ячейки Вороного и считается объем пересечения этих ячеек с ячейками исходной диаграммы. Веса суммирования полагаются пропорциональными посчитанным объемам (см. рис. 7). Такой метод подсчета весов позволяет лучше учитывать ситуации, когда точки с известными значениями распределены неравномерно, т.к. kNN полагает вклад точек, находящихся на одинаковом расстоянии от нужной, равным, а метод естественной окрестности уменьшает вклад находящихся рядом друг с другом точек.

Метод Сибсона плохо работает в случаях, когда объем пересечения ячеек условнобесконечен. Это происходит в случаях, когда добавляемая точка лежит на границе или за ней, и ее ячейка Вороного «уходит на бесконечность». Строго говоря, объем ячейки Вороного конечен, если добавленная точка лежит внутри выпуклой оболочки множества остальных точек, однако на практике удобнее считать бесконечными ячейки, линейные размеры которых значительно превышают средний шаг сетки. Описанный выше метод фильтрации точек при помощи граничных узлов и К — d дерева позволяет отбрасывать такие точки в большинстве случаев, а добавление виртуальных узлов к начальной диаграмме предотвращает появление ячеек Вороного бесконечного объема для всех невиртуальных точек (как исходных, так и тех, значение в которых интерполируется). Построение диаграммы Вороного связано с триангуляцией Делоне. Обе эти задачи в трехмерном пространстве значительно сложнее, чем в двумерном. Кроме того, как и у других геометрических методов, при их реализации нужно или аккуратно учитывать возможность появления параллельных линий и плоскостей (а также почти параллельных, пересекающихся на большом расстоянии от рассматриваемой области пространства), или накладывать дополнительные требования на исходные данные. Для предотвращения проблем, связанных с параллельностью, можно случайным образом сдвигать точки с известными значениями на небольшое расстояние. Под небольшим расстоянием здесь понимается расстояние на 2-3 порядка меньшее, чем характерное расстояние между самими точками.

5.3.    Барицентрические координаты

В качестве коэффициентов интерполяции можно использовать барицентрические координаты точки в содержащем ее симплексе (соответственно, в суммировании будут участвовать значения в узлах, являющихся вершинами этого симплекса). Поскольку мы имеем дело с прямоугольными сетками, то вместе с поиском содержащего симплекса происходит поиск и содержащей ячейки сетки. Для поиска содержащей ячейки мы просматриваем ячейки, соответствующие ближайшим к точке узлам. Поиск этих точек мы осуществляем при помощи все того же К — d дерева.

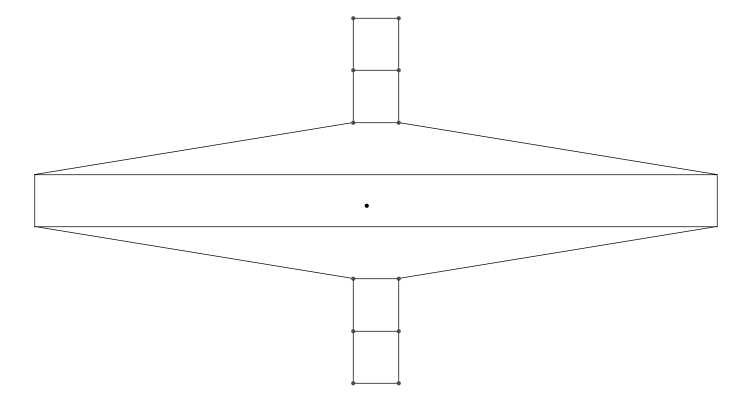
Рис. 8. Примеры успешного и неудачного поиска содержащей ячейки перебором ближайших узлов

На рис. 8 красным цветом выделены ближайшие узлы (которые будут просмотрены при поиске). Видно, что такой способ поиска не является универсальным, можно построить сетку, для которой он не сработает. Однако такие сетки зачастую являются «плохими» — шаги сетки по одной или по разным осям значительно отличаются. Поэтому мы не выполняем интерполяцию на них, хотя это можно было бы делать, например, просматривая узлы, начиная от ближайших поиском в ширину.

6.    Параллельные вычисления

В работах [3, 4, 10] рассматриваются вопросы распараллеливания сеточнохарактеристического метода в случае использования нескольких расчетных сеток, а случай одной сетки рассмотрен в [2]- В [7] проведен анализ различных способов использования массово-параллельных архитектур для моделирования с использованием наложенных сеток. Интерполяция значительно уступает моделированию в вычислительной сложности. Кроме того, она выполняется один раз для каждой конфигурации физического пространства и описывающих его сеток, запускать ее повторно для моделирования с другими начальными условиями не требуется. Все это значительно снижает полезность параллельной реализации интерполяции. С другой стороны, используемые нами методы интерполяции хорошо подходят для параллельного выполнения, поскольку все они хорошо разбиваются на три этапа: подготовка и построение некоторых структур данных по координатам точек; независимая интерполяция во всех интересующих нас точках с использованием этих структур; и, наконец, сбор и объединение результатов. Более того, используемые структуры данных никак не модифицируются в процессе интерполяции (кроме диаграмм Вороного в методе естественной окрестности, однако и там это можно обойти). Таким образом, процесс интерполяции без особых проблем может выполняться как в многопоточных, так и в массово-параллельных средах, если это необходимо. В данной работе используется реализация для многопоточных сред, поскольку размеры используемых сеток сравнительно невелики, и потенциальный выигрыш от использования систем с разделяемой памятью не превышает накладных расходов на использование этих систем. Тем не менее для сеток большего размера такая реализация может быть целесообразна.

7.    Сравнение методов в модельной задаче а) б)

Рис. 9. Взаимное расположение сеток в двух проекциях

В геофизике хорошо известна асимметричная задача Лэмба о распространении сейсмической волны в эластичном полупространстве, ограниченном свободной поверхностью. Для моделирования этой задачи мы использовали сеточно-характеристический метод, сравнивая применения наложенной сетки для описания свободной поверхности и применение граничных условий на основной расчетной сетке (см. рис. 9). Мы использовали в качестве наложенной равномерную прямоугольную сетку, ребра которой повернуты на угол 18^о относительно ребер основной сетки. Для сохранения взаимного расположения в системе источника, свободная поверхность, вектор источник-приемник и источник-первый узел сетки были повернуты вокруг оси, проходящей через источник и параллельной оси Oz. В качестве источника возмущения использовался импульс Риккера частоты 14.5 Гц. Было промоделировано распространение упругих волн в среде со следующими физическими параметрами: V_s = 3200 м/с, V_p = 1847.5 м/с, р = 2200 кг/м³ в течение 490 шагов At = 5 • 10^-4 с.

В постановке с повернутой наложенной сеткой было проведено моделирование распространения упругих волн при различных методах интерполяции, примененных для интерполяции значений из основной в наложенную и из наложенной в основную сетки. В сравнении участвовали следующие методы: метод естественной окрестности (Nat. neighbour), метод ближайших соседей (kNN), интерполяция в барицентрических координатах (Barycentric).

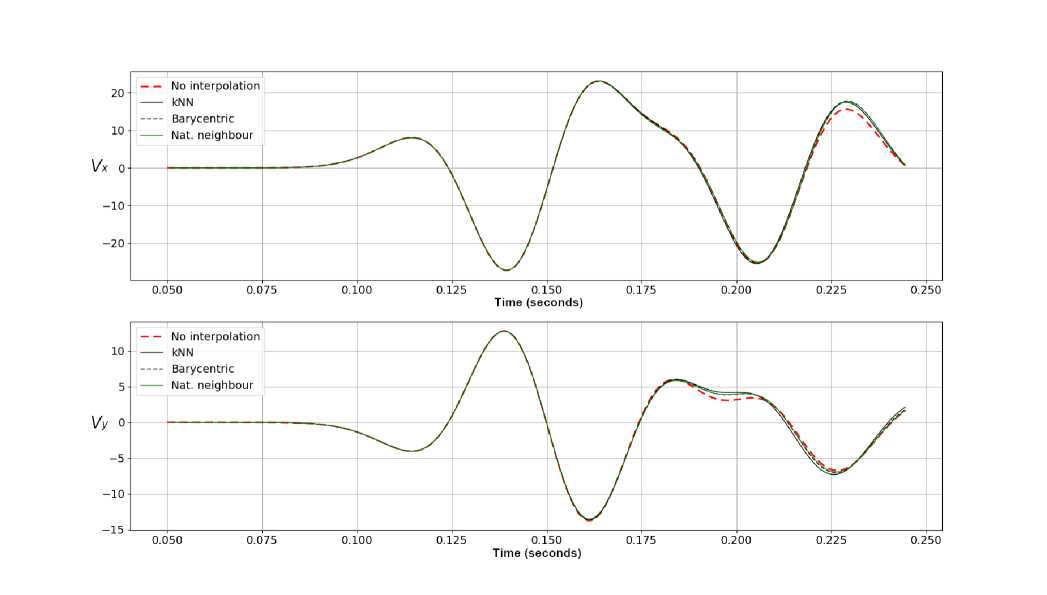
Рис. 10. Сравнение значений V_x и Ту на приемнике при моделировании двумерной задачи Лэмба с использованием различных методов интерполяции

Результаты сравнения различий значений принимаемого приемником сигнала для различных методов интерполяции приведены в сравнении с решением задачи Лэбма сеточнохарактеристическим методом без использования метода наложенных сеток и представлены на рис. 10. Как видно из этого графика, все представленные методы интерполяции показали результаты, сравнимые с результатом, полученным в случае применения классического сеточно-характеристического метода. Пики возмущения отраженной от свободной поверхности волны совпадают по времени регистрации приемником во всех методах.

Различия в абсолютных значениях V_z и Vy плохо различимы на графике показаний приемника, поэтому на рис. 11 приведены графики абсолютной погрешности — разности показаний приемника в постановке с повернутой сеткой и интерполяцией и в эталонном случае (без поворота сетки и интерполяции). Можно видеть, что погрешность невелика, до t = 0.2 с, когда через приемник проходят волна от источника и отраженная волна, однако увеличивается, когда приходят паразитные волны, отраженные от поглощающих границ.

Перейдем к более детальному сравнению использованных методов интерполяции.

8.    Сравнение различных методов интерполяции

В сравнении методов интерполяции мы будем рассматривать два основных критерия. Первый — это относительная ошибка абсолютных значений Vz и Vy, регистрируемых приемником возмущений в задаче Лэбма, описанной выше. Вторым важным фактором сравнения методов интерполяции является их вычислительная сложность, выражающаяся во времени, затрачиваемом для вычисления весов интерполяции. Рассмотрим график, представленный на рис. 11 и отображающий относительные ошибки методов интерполяции. Как видно, результаты, наиболее близкие к эталонным, получены при использовании интерполяции барицентрическими координатами, в то время как метод ближайших соседей дает наибольшую погрешность. Однако погрешности всех методов сравнимы и отличаются не сильно, так что можно сделать вывод о том, что все методы вполне применимы на практике.

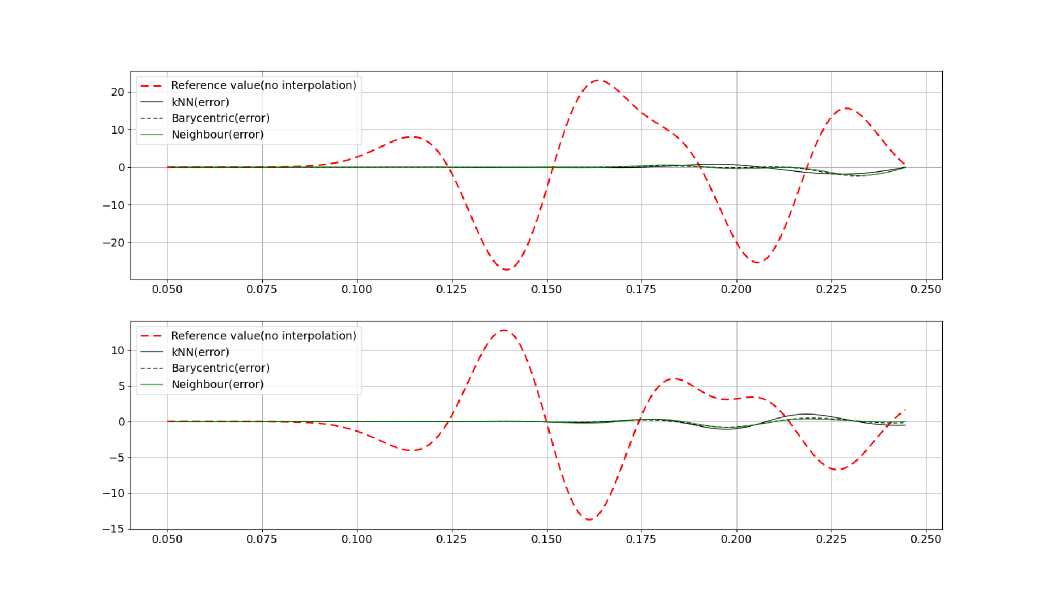
Рис. 11. Абсолютные погрешности методов (разность показаний приемника, с эталонным методом без интерполяции) и показания приемника, для наглядности

Для решения рассматриваемой в нашей работе задачи использовались основная регулярная сетка, состоящая из кубов размером 135 х 135 х 101 узлов, и наложенная повернутая сетка, состоящая из кубов с такой же длиной граней размером 108 х 5 х 102 узлов. Все вычисления производились на одном и том же оборудовании, что позволяет проводить относительное сравнение вычислительной сложности методов в приведенной постановке задачи. В таблице ниже представлены результаты сравнения скорости вычисления описанного эксперимента, для различных методов интерполяции.

Метод	Из основной в наложенную, с	Из наложенной в основную, с
Метод Сибсона.	_	249.81
Метод ближайших соседей	2.32	3.32
Барицентрические координаты	0.31	0.56

Интерполяция методом барицентрических координат работает быстрее всего. Это ожидаемо, поскольку это самый простой из используемых методов. Метод ближайших соседей работает медленнее. Это по большей части связано с тем, что он в любом случае требует построения К — d дерева, на что уходит заметная часть времени. Построение К — d дерева замедлило бы и интерполяцию барицентрическими координатами, но поскольку используемая нами для задачи Лэмба наложенная сетка является структурированной и просто повернута, то мы можем значительно ускорить поиск содержащей точку ячейки. Долгая работа, метода. Сибсона обусловлена, в первую очередь его значительной вычислительной сложностью. Вторая причина — то, что используемая нами реализация работает в один поток, из-за. чего недоиспользует аппаратные ресурсы. Тем не менее время интерполяции методом Сибсона. все еще меньше, чем время моделирования, так что низкое быстродействие не мешает применению метода на практике. Также было обнаружено, что наша реализация метода Сибсона отрабатывает на одних и тех же сетках за существенно разное время (но с одинаковыми результатами), из-за чего не удалось провести измерение времени ее работы из основной сетки в наложенную (разброс составлял более 50 процентов от среднего времени, что делало измерение бессмысленным). Нам не удалось установить причину этой проблемы, однако поскольку она не влияет на результаты моделирования, было решено оставить все как есть.

9.    Пример моделирования сложной топографии

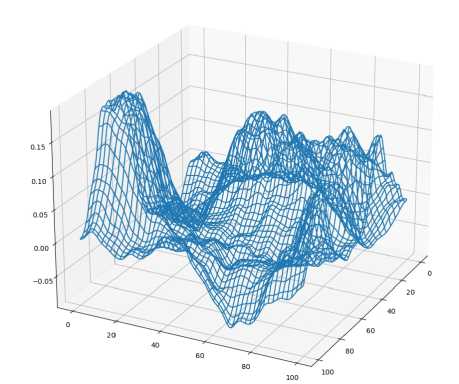
Рис. 12. Пример моделируемой топографии

Используемая для примера поверхность представлена на рис. 12 в виде двумерной криволинейной сетки. Размеры области составляют 600 х 600 метров, перепад высот — 218 метров. Трехмерная криволинейная наложенная сетка состоит из таких же слоев с шагом по вертикали 4 метра. Размеры наложенной сетки — 150 х 150 х 8 узлов, основной — 150 х 150 х 300 узлов с шагом 4 метра по всем осям. Для расчета использовался один вычислительный узел с 8 ядрами и 64 Gb оперативной памяти, расчет занял примерно 40 минут.

а)                                    б)                                    в)

г)                                    д)                                    е)

Рис. 13. Волновые картины, полученные в ходе моделирования в разные моменты времени

На рис. 13 представлены волновые картины в верхней части одного из срезов основной сетки и на поверхности наложенной сетки, описывающей поверхность рассматриваемого участка в различные моменты времени. В данном эксперименте источник находится примерно на глубине 750 м от низшей точки поверхности, для наглядности приведена толвко верхняя частв моделируемой области.

10.    Заключение

В статве приведен анализ основных сложностей трехмерной интерполяции и причин их возникновения, описаны несколвко реализованных и используемых методов. Была проведена оценка относительной точности метода наложенных сеток с применением различных методов интерполяции на примере задачи Лэмба. Так же была измерена скорость расчета интерполяционных коэффициентов в рассматриваемой постановке. Кроме того, в данной работе приводится предложение прикладного применения метода наложенных сеток применительно к реалистичной задаче моделирования распространения упругой волны под свободной поверхностью, имеющей сложную топологию. Список перечисленных методов не является исчерпывающим. В частности, в него не попали полиномиальная и сплайн-интерполяция. Тем не менее предложенные методы широко применимы и используются на практике. Анализ влияния различных методов интерполяции на сходимость автором пока не проводился, но может служить темой дальнейшего исследования.