Применение метода ньютона для решения задач страхования жизни и аннуитетов

В современном мире, где финансовая стабильность играет ключевую роль в планировании будущего, вопросы страхования жизни и аннуитетов становятся все более важными для индивидуальных лиц и компаний, в особенности это будет проявляется при развитии экономики, как происходит у нас в Кыргызстане. Эти финансовые инструменты не только обеспечивают защиту от неожиданных событий, но и способствуют созданию устойчивого финансового фундамента на долгосрочную перспективу.

В контексте математического анализа и решения финансовых задач, метод Ньютона давно зарекомендовал себя как мощный инструмент. Применение метода Ньютона в области страхования жизни и аннуитетов может дать толчок для более точного определения показателей задач страхования и управления финансовыми рисками.

Покажем применение метода Ньютона для решения задач, связанных со страхованием жизни и аннуитетами в условиях

^S n =

Кыргызстана. Мы проанализируем применимость данного метода к различным сценариям страхования, а также рассмотрим примеры его использования в практических задачах страхования жизни опираясь на таблицу смертности Кыргызстана [3].

Основные формулы задач страхования жизни описаны в работах [1, 2, 4, 5]. Применение таблиц смертности приведенных в [3], к сожалению, невозможны из-за отсутствия данных для дробных возвратов, поэтому в работах [6, 7] приведены примеры интерполяции дробных возрастов, имеющих выпуклость вверх, которые подходят для данных из Кыргызстана.

Рассмотрим задачу определения процентной ставки при условии определенности остальных параметров. Для начала рассмотрим задачу с финансовыми аннуитетами для определения накопленной величины S_n , при известных параметрах (процентная ставка - i, ежепериодные платежи - р и срок п), которая имеет вид:

Р•((1 + i)ⁿ - 1) i

В данной формуле все параметры легко определяются, кроме процентной ставки. Для определения процентной ставки выразим данное выражение в виде:

i • Sn — Р • ((1 + i)n — 1) = 0

Рассмотрим данное уравнение как функцию от аргумента i, и выразим его итерационной формулой Ньютона, получим:

ⁱ k+1 ⁱ k

ⁱ k ' -^ п ^- Р • ⁽⁽¹ + ⁱ k ^{)n —} 1) S_n-p-n-(1 + i k ^)n-1

Полученная итерационная формула позволяет определить процентную ставку, если известны другие параметры, в задачах финансовых аннуитетов.

Пример. Родители для своего сына с момента, когда ему исполнился 1 год,

начали откладывали в банк 40 000 в год в течении 18 лет, и накопили 2 229 988,60 рублей. Чему равна процентная ставка.

Решение.

Используя вышеуказанную формулу для данного примера, получим формулу:

ⁱ k+1     ⁱ k

i_k • 2229988,6 - 40000 • ((1 + i_k) ¹⁸ - 1) 2229988,6 - 40000 • 18 • (1 + i_k) ¹⁷   '

Для первоначального приближение возьмем i0 = 0,3, что соответствует 30%. Запустив итерационный процесс, получим:

i 1 = 0,236902081 i₂ = 0,185124714 i₃ = 0,14790489

i4 = 0,127227947 i5 = 0,120639302 i6 = 0,120005586

i7 = 0,12

Как видим уже на пятой итерации при округлении до тысячных мы получили уже точное значение.

Теперь, покажем применение метода Ньютона для задач страхования жизни.

Для этого рассмотрим задачу страхования жизни с выплатой в конце года смерти выгода приобретателю. Формула определения страховой премии при этом будет иметь вид:

от

P = V •

z k=0

Qx+k k+i

—— v^k+1 .

В данной формуле V - это разовая выплата выгода приобретателю, Qx -количество людей умерших в возрасте х лет, lx - количество людей, доживших до возраста х лет и конечно же v - дисконт- ный множитель, равный . Все параметры легко вычисляемы в данном примере, конечно как и в прошлом примере сложно определить только процентную ставку. И в общем виде его не возможно выразить аналитически. Поэтому здесь также как и в первом случае применим методо Ньютона для определения процентной ставки, правда здесь расчеты еще сложнее, так как каждая итерация требует вычисления суммы.

Конечно легче здесь выразить формулу не для процентной ставки а для ставки дисконта, для начала преобразуем нашу формулу к виду

V •

^Q x+k_vk+1 k=0 ^lx

-P = 0

Теперь применим метод Ньютона, получим формулу vm+1

^v m

у . у ° Qx+k к+1 _ p ^{V Y} k=0 l   ^v m     ^P

v-ik+D-vooJ+^vm

1 x

Где после упрощений получим

E°  0x+k_-,,k+1 _ n vm+1

^v m

k=0  [   vm

(k + D-Y^o^vm 1 x или vm+1

^v m

Pv

+---1—

(k+v-YkoJ+^vm

1 x

Последняя формула, является самой менее требовательной к системам, хоть и выглядит более громоздко.

Давайте теперь приведем листинг программы, на языке программирования Python, для определения процентной ставки для финансовых аннуитетов:

n = int(input('Введите срок: '))

p = float(input('Введите ежепериодный платеж: '))

s = float(input('Введите накопленную величину: '))

eps = 10**(-int(input('Введите точность (количество знаков после запятой): '))+1)

i = float(input('Введите первоначальное приближение: '))

pr = i-(i*s-p*((1+i)**n-1))/(s-p*n*(1+i)**(n-1))

k = 1

while (abs(pr-i)>eps and k<100):

print('i({}) = {}'.format(k,pr))

k += 1

i = pr pr = i-(i*s-p*((1+i)**n-1))/(s-p*n*(1+i)**(n-1))

Листинг программы как мы с вами видим простой но эффективный. Если запустить в данными приведенными в примере выше мы получим следующий результат:

Введите срок: 18

Введите ежепериодный платеж: 40000

Введите накопленную величину: 2229988.6

Введите точность (количество знаков после запятой): 5

Введите первоначальное приближение: 0.3

i(1) = 0.2369020811906567

i(2) = 0.18512471422569377

i(3) = 0.14790488975931998

i(4) = 0.127227946916844

i(5) = 0.12063930180323569

i(6) = 0.12000558621157839

Для решения задачи определения процентной ставки в страховании жизни представим таблицу смертности Кыргызстана из [3]. Представим скриншот таблицы смертности Кыргызстана на 2020 год.

Таблица 2.21: Таблицы смертности и ожидаемой продолжительности жизни населения Кыргызской Республики в 2020г.

Возраст (лет)	Числа доживающих до точного возраста х лет	Число умирающих в интервале возраста от х до х+1 лет	Вероятность умереть в интервале возраста от х до х+п	Вероятность дожить до следующего возраста х+1 лет.	Число живущих в возрасте от х и до х+1 лет	Число человеко-лет жизни в возрасте х лет и старше	Ожидаемая продолжите ль ность жизни населения, число лет
X	1х	dx	qx	Рх	Lx	Тх	ех

Оба пола

0	100 000	1425	0,0143	0,9857	98 709      7 165 211	71,7
1	98 575	102	0,0010	0,9990	98 480      7 066 502	71.7
2	98 473	57	0,0006	0,9994	98 420      6 968 022	70.8
3	98 416	43	0,0004	0,9996	98 376      6 869 602	69,8
4	98 373	30	0,0003	0,9997	98 345      6 771 226	68,8
95	780	274	0,3514	0,6486	643      ____1 724	42
96	506	183	0,3609	0,6391	415     ____1081	2,1
97	323	121	0,3741	0,6259	263           667	2.1
98	202	77	0,3827	0,6173	164            404	20
99	125	49	0,3927	0,6073	100           240	1,9
100	76	76	1,0000	0,0000	140            140	1,3

Рис. 1. Скриншот таблицы смертности

Из данного скриншота видно, что нам необходимы данные со столбцов два и три, где указаны число доживщих и умерших в указанных возрастных интервалах. К сожалению, не возможно в ручную произвести расчеты, но тем не менее можно запрограммировать и получить

программу для определения процентной

ставки.

Построим блок схему определения дисконтного множителя методом Ньютона. Так как блок схема слишком длинная, мы разделим блок схему нашего алгоритма на 2 части, которые приведены на рисунках 2 и 3.

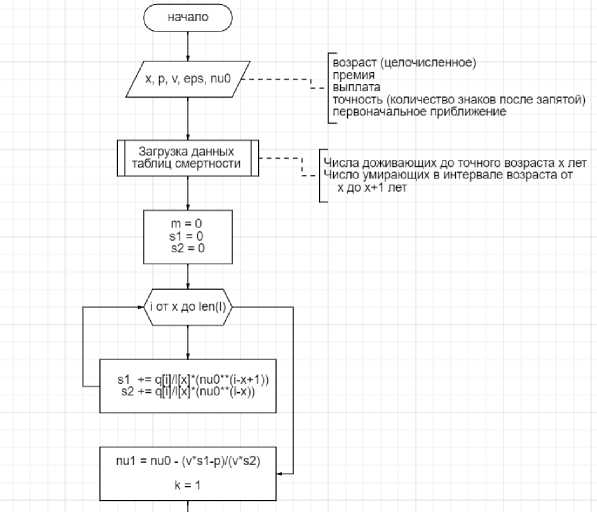
Рис. 2. Первая часть блок схемы метода Ньютона

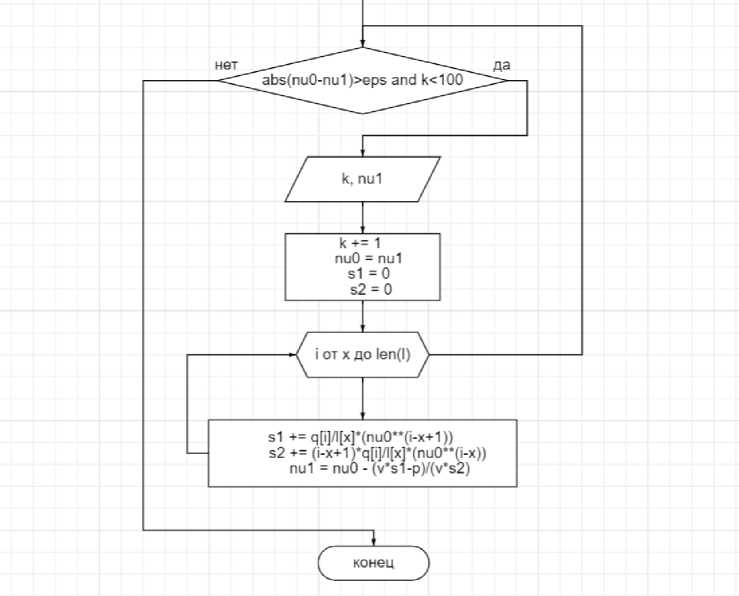
Рис. 3. Вторая часть блок схемы метода Ньютона

На основе указанных на рисунках 2 и 3 алгоритма, приведем листинг программы на языке программирования Python.

Листинг программы:

""" Чтение данных с таблиц смертности для дробных возрастов.

Используем библиотеку xlrd для загрузки. """

wsheet = wbook.sheet_by_index(0)

l = []

q = []

# Загрузка доживщих и умирающих в целых возрастных интервалах for i in range(1,103):

x = int(input('Введите возраст (целочисленное): '))

p = float(input('Введите премию: '))

v = float(input('Введите величину выплаты: '))

eps = 10**(-int(input('Введите точность (количество знаков после запятой): '))+1)

nu0 = float(input('Введите первоначальное приближение: '))

m = 0

s1 = 0

s2 = 0

for i in range(x,len(l)):

s1 += q[i]/l[x]*(nu0**(i-x+1))

s2 += q[i]/l[x]*(nu0**(i-x))

nu1 = nu0 - (v*s1-p)/(v*s2)

k = 1

while (abs(nu0-nu1)>eps and k<100):

print('nu({}) = {}'.format(k,nu1))

k += 1

nu0 = nu1

s1 = 0

• s2 = 0

for i in range(x,len(l)):

s1 += q[i]/l[x]*(nu0**(i-x+1))

s2 += (i-x+1)*q[i]/l[x]*(nu0**(i-x))

nu1 = nu0 - (v*s1-p)/(v*s2)

При запуске программы и вводе контрольных данных мы получим следующий результат:

Введите возраст (целочисленное): 20

Введите премию: 6795.392

Введите величину выплаты: 500000

Введите точность (количество знаков после запятой): 6

Введите первоначальное приближение: 0.89

nu(1) = 1.0663637403130808

nu(2) = 1.0488847474208634

nu(3) = 1.0312860782553877

nu(4) = 1.0134948422346186

nu(5) = 0.995411574023607

nu(6) = 0.9769164189857511

nu(7) = 0.9579271436483767

nu(8) = 0.938630882845695

nu(9) = 0.920152623955502

nu(10) = 0.9055895788018345

nu(11) = 0.8986236946142384

nu(12) = 0.8974613965728628

nu(13) = 0.8974347007717958

Здесь видно, что при точности £ = 10 ^-6 ответ получим на 13 шаге. И это учитывая факт, что первоначальное приближение было более точным. Но при изменении первоначального приближения на одну сотую, получим ответ только на 26 шаге.

Как мы с вами видим, мы можем с помощью метода Ньютона вычислять процентную ставку или ставку дисконта для задач страхования жизни и аннуитетов, данную работу можно использовать на уроках по численным методам или в курсах актуарной математики, с применением ЭВМ.