Применение метода повторного квантования к одному классу нефуксовых уравнений

Эта статья посвящена развитию метода, который применяется для решения одной из фундаментальных проблем аналитической теории дифференциальных уравнений, а именно проблеме построения равномерных асимптотик решений уравнений с мероморфными коэффициентами в окрестности иррегулярных особых точек. Этот метод называется методом повторного квантования [1, 2].

Проблема построения равномерных асимптотик решений дифференциальных уравнений в окрестностях особых точек была сформулирована Пуанкаре в работах [3, 4].

(О 2025 Коровина М. В., Смирнов В. Ю.

В этих работах он рассматривал случай, когда иррегулярной особой точкой является бесконечность, а именно задачу для уравнения вида a-(r)

ddr

u(r) + a --i

ddr

u(r) + ... + a i (r)

ddr

u(r) + ... + a o (r)u(r) = 0,

где a i (r) , i = 0,... ,n , — голоморфные функции. Задача, сформулированная Пуанкаре, заключалась в построении асимптотик решений уравнения (1) в окрестности бесконечности в случае, когда a n (r) = 1 . Как известно, бесконечность, вообще говоря, является иррегулярной особой точкой. Эта задача решена в работах [5, 6] с помощью метода повторного квантования. В общем случае, когда коэффициент a _n (r) является произвольной голоморфной или мероморфной функцией, задача построения асимптотик в окрестности иррегулярной особой точки является более сложной и требует дополнительных возможностей метода повторного квантования.

Данный подход был создан для построения асимптотик решений дифференциальных уравнений в окрестности иррегулярных особых точек в случае, когда корни основного символа дифференциального оператора являются кратными. Напомним определение основного символа.

Без ограничения общности будем считать, что особой точкой уравнения (1) является r = 0 . В работе [7] показано, что уравнение (1) может быть приведено к виду

H^^-rM dr) = (^-r ^k+1 dr) “ ^{+ g} a^r) (^-r ^k+1 dr) i           ⁽²⁾

Здесь k = - 1, 0,1, 2,... , а через at(r) обозначены соответствующие голоморфные функции. B работе [7] найдено минимальное значение k , т. е. минимальный порядок вырождения и коэффициенты этого уравнения. Если в представлении (2) уравнения (1) минимальное k = — 1 , то по классификации особых точек, введенной Пуанкаре, получим, что точка r = 0 не является особой. Если k = 0 , то особая точка r = 0 является регулярной. Как известно [8], в окрестности регулярной особой точки асимптотика решения является конормальной. Если k ∈ N, то особая точка является иррегулярной, в этом случае запишем оператор (2) в виде

H fr, — r k⁺¹ d- ^ = kn ( f — 1 r ^k+1 d- ) + ^g ai(r)T¹- (— 1 r ^k+1 d- ^   .

\ dr J \\ к     dr J    i=0      к^{- г} \ k dr J J

Основным символом дифференциального оператора H ri'. —r^{k +} dr ) является функция

H o (p)= P ^- + ^g ^ p i .

i=0

В случае, когда основной символ имеет только простые корни, асимптотики решений в окрестности особых точек были получены в работе [9].

Однако методы из [9] оказались неприменимыми в ситуации кратных корней, кроме случая уравнений второго порядка. В работе [10] вопрос о построении асимптотик решений для уравнения второго порядка с произвольными голоморфными коэффициентами решен.

Для решения проблемы кратных корней в последние годы был создан метод повторного квантования. Суть этого метода состоит в том, что делается преобразование Лапласа — Бореля и доказывается теорема о бесконечной продолжимости решений полученного уравнения (для обыкновенных дифференциальных уравнений это доказано в [11]). Далее еще раз применяется преобразование Лапласа — Бореля и для итогового уравнения строятся асимптотики, которые позволяют найти асимптотики исходного уравнения. Иными словами, суть метода повторного квантования состоит в том, что преобразование Лапласа — Бореля делается два раза. Т. е. сдвинув корень основного символа pj с помощью экспоненциальной подстановки в точку ноль, делается преобразование Лапласа — Бореля и получается интегро-дифференциальное уравнение относительно функции данного преобразования функции Uj (r), которое мы будем обозначать через Uj (p). При этом точка p = 0 будет особой точкой полученного уравнения. Она может быть как регулярной особенностью, так и иррегулярной. Если она регулярна, то, как известно, асимптотика функции Uj (p) является конормальной, если иррегулярной, то, чтобы найти асимптотику этой функции в нуле, делается преобразование Лапласа — Бореля второй раз. При этом мы получаем интегральное уравнение относительно функции Uj (q), которая является преобразованием Лапласа — Бореля функции Uj (p). Для полученного уравнения, с помощью метода последовательных приближений строится асимптотика его решения в окрестности корней главного символа. Найдя асимптотику функции Uj (q), и затем, сделав обратное преобразование Лапласа — Бореля, строится асимптотика функции Uj (p) в окрестности нуля. Эта асимптотика может быть ВКБ-асимптотикой или иметь более общий вид и содержать экспоненты с дробными степенями. Поэтому возникает необходимость вычисления обратного преобразования Лапласа — Бореля от функций вида n ea/p k g(p~), где n,k G N, a G C.

Рассмотрим пример, который иллюстрирует применение метода повторного квантования к построению асимптотики решения дифференциального уравнения в окрестности иррегулярной особой точки:

(—r ² -f—^ u — cr ² u = 0. dr

Применив преобразование Лапласа — Бореля к уравнению (3), получим p5u — cr2U = f (p).

Приведем (4) к виду

(dp) ^{p 5} u^—cU=(dp) f ^{( p )} -

Здесь f (p) — произвольная голоморфная функция. Применим метод повторного квантования. Так как выполнено равенство

(dp) ^{p 5 u} =

/ 5 d V /5\ 3 / 5 d \

\ p 2 — I и +10--p 2 p 2— u + 20p ³ u,

V dp J      V 2/ V   dp J

то уравнение (5) можно переписать в виде

( 2 5 d V 2 (     5\ 3 / 2 5 d\

- ^—3 ^p 2 dp) ^{u —} Ц^{10 —} + ^p 2 + 3 ^p 2 dp)

~   80

U + —p и —

^{4 cU}= ( ² Tp ) ^{f ( p )} .    ⁽⁶⁾

p

Основной символ дифференциального оператора в (6) равен q ² — 4 c , т. е. основной символ имеет два простых корня q 1,₂ = ± | / с . Асимптотика решения уравнения (6) в окрестности регулярной особой точки p = 0 имеет вид

2 /^    °°             - 2 /7    ^

u(p) ^ exp -Ц- p ⁷ £ b ¹ p i + exp —3g— p ⁷ £ b ² p i .

P ²      i=o               p ²       i=0

Для того, чтобы найти асимптотику решения (3), надо найти обратное преобразование Лапласа — Бореля от выражения вида exp (pO /- )p ⁷ £° =₀ b i p i , где m,n G N , a G C, a G R. Это будет сделано ниже в теореме 2.

• 2.    Основные определения и вспомогательные утверждения

В этом параграфе мы дадим определения основных понятий, которые будут использованы в статье (см. подробнее [12, 13]).

Определение 1. Аналитическая на S R_,ε функция f , имеет не более, чем k -экспоненциальный рост, если существуют такие неотрицательные константы C и α , что в секторе S R_,ε выполнено неравенство

¹ | f | < Ce ^{α | r | k} .

Обозначим через E k ( S r,_£ ) пространство функций k -экспоненциального роста. Если г может быть выбран любым 0 < г ^ 2п , то будем обозначать это пространство как E k ( S r ) ,и E ( S r )= E 1 ( S r ) .

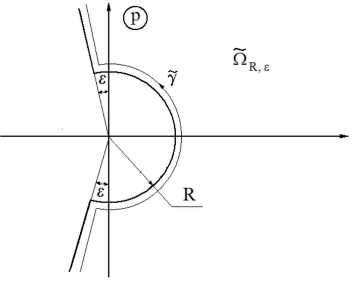
Рис. 1. Контур Y и область ^ r,_£ .

Определение 2. к -преобразованием Лапласа — Бореля функции f (r) G Ek (Sr,£ ) называется отображение Bk : Ek (Sr,£) ^ E(Qr,£)/E(C) такое, что r0

^f = B k f = / e ^- p^/r k f (r)rd +i ■

Обратное k -преобразование Лапласа — Бореля определяется формулой

B - f =^i / e p/r k ^f (p

Y

Контур Y изображен на рис. 1.

Определение 3. Функция f называется бесконечно-продолжимой , если для любого числа R существует такое дискретное множество точек Z R в C, что функция f аналитически продолжается из первоначальной области определения вдоль любого пути длины меньше R , не проходящего через Z R .

Определение 4. Элемент f пространства E k ( S r,^ называется k - ресургентной функцией , если его k -преобразование Лапласа — Бореля f = B k f является бесконечно-продолжимым.

В работе [14] была доказана следующая теорема.

Теорема 1. Пусть f — ресургентная функция, тогда решение уравнения H (— r k+1 dr ,Г u = f является ресургентной функцией в пространстве E ( S r ) . Если полином H q (p) имеет простые корни в точках p 1 ,..., p m , тогда асимптотика решения в пространстве E ( S r ) однородного уравнения H £r k⁺¹ dr ,r) u = 0 имеет вид: при k = 1

u(r) ^ £exp (pj) r^j £ bjri,(7)

j=1       r при k > 1, k G N m      /     k—1 1 \

u(r) ^ £ exp pj + £ rj-r] r £ bjri,(8)

j=1     \      i=1      /i=0

при k = mm , m G N , n G N , m > n,

(m—k—1 1     \

-j + £ i raj £ bjri,(9)

r k     ■-irk1-/ i=1 '         /i=0

где сумма берется по объединению всех корней полинома H q ( p ) . Здесь через b j , a j , j = 1,... ,m, обозначены некоторые числа.

Введем обозначение:

rn = BrnB-\(10)

В работе [14] было доказано равенство

Рn rfp) = (—1)n [ (p—f (p‘) dp'

^{1 ( n})

Р 0

В частном случае

p

Г ~          .

rf (p) = - J f (P ) dp .                                (12)

p 0

• 3.    Основные результаты

В этом параграфе мы сформулируем и докажем следующую теорему.

nk

Теорема 2. Асимптотика функции B^p e a/p g (p), k G N, n G N, k ^ n, и a, a G C, в окрестности нуля имеет вид n+k     /           mk+n—1     j \^

£ exp I —jj--+ £ —ji .— j r^j   bjri.(13)

/         I mk + n 1 1               mk+n-г 1 I            i\ / j=1      \r n+k          i=1 r k+n/ i=0

Здесь a j , j = 1,... ,k + n, — корни полинома p n+k + ( — 1) ⁿ⁺¹ (m — 1) n ( Of ) n ( n+k ) n⁺k , a aj , aj — соответствующие числа, £ “ ₀ b^jг^г — асимптотический ряд.

⊳ Рассмотрим уравнение

(-- m ^U + C n - 1 r m-1    d^

/ J \ k+^n-2                          / и \ k⁺¹

+ C n - 2 r ^2(m-1) ( -r m d-\ U + ... + C i - n-^m-¹ — —r m d     U

+ Cr ^{n(m - 1)} u + C ₀ r ^n(m-1) (—-r ^m dd- ) u = 0.

Здесь через C i , i = 0,...,n — 1, и c обозначены некоторые константы. Перепишем уравнение в виде

- m—1

r m ^d dr

n+k

U + C n-1

m — 1

r m - 1

— m—1

r m ^d dr

k+n - 1

u

^{+ C n - 2} (m — 1) ²

_r 2(m - 1)

(

-

m

— 1

r ^{m d} dr

k+n - 2

u

!                 !                            1

⁺ '" ^{+ C 1} (m — 1) n - 1

r (n - 1)(m - 1)

( Ч rm T У^ u m — 1 dr

+ C 71—т r ^n(m-1) u + Co  -- 1—— r ^n(m-1)

(m — 1) ^{n+k            0} (m — 1) ⁿ

— m—1

r ^m -d] U = 0. dr

Сделаем в (15) преобразование Лапласа — Бореля

Pp2

p n⁺k u + ( m o ⁽ _— 1) _{2 n} У • • • У P 1 u(p 1 ) dp 1 ■■■ dp n 11

n-1 pp

⁺ ( mm _{— 1})2( n - 1) У ••• У ^{p k+1 u ( p} 1 ^{) dp} 1 ••• ^dp n-1 11

n - 2 ^{p p2}

• +    ••• + (m2— 11)2(n-2) У ■” У Pk+2u(P1) dP1dP2 . . . dPn-2

p

• +    ... + Cn-^—1 / pk' u p dp1 (m - 1)21

pp

• ^{+    C ( — 1) n} ( _{m —} 1) 2 n + k У ... У u ⁽ P 1 ) dP 1 ... dP n = ^{f (} P)

Через f (p) обозначена произвольная голоморфная функция. Продифференцируем n раз уравнение (16). Тогда

(d- Г _P n+k u + c ^{o (} - ^{1) n} p k u + c 1 ⁽ — ^{1) n-1}   m _p k₊i u

\dp)           (m — 1) ²ⁿ        (m — 1) ^2(n-1) \dp)

C2( - 1) ⁿ - ²   P У p k+2 u

(m — 1) ^2(n-2) \dp )

^c n - 1 ^{( —}1)

⁺ ■■■ ⁺ (m — 1) ²

( d An ^-1 k+n-1       ( — 1) n          d^d

(dp) p    u ⁺ ( m - 1)* + * cu = U) f'

Покажем, что можно выбрать константы c , C i , i = 0,...,n — 1 так, чтобы функция k

U(p) = p ^ e p ⁿ" являлась решением (17), для этого подставим эту функцию в данное уравнение. Тогда получим соотношение относительно констант c , C i , i = 0,..., n — 1 :

• {„ n^+k ।  „.n^a+k - k  ।  „.n„.++-— ।  „n-ff+k-    ।       ।  „п^стА  ।     c n^{-1 (}   1)

• ^a 0 p   ^{+ a} i p    ^{n + a} 2 p     ^{n + a} 3 p     ^{n +} ... ^{+ a} n p J ⁺ ( m _{— 1} ) ₂( _{n -} 1)

• x {a n^-1 id'k + an^-1 id'k k + an^-1 id ' ^k 2k + an^-1 id ' ^k 3 k +    + a^n—1 id ' ^k ( n^ А

• aQ p      a1 p         a2 p         a3 p         ... an1p

+ _{( m} '   ■          ' +         ' ^k +• • •+a n - “ А

• c ^{1 ( — 1) n-1}    { 1 ст+k ,   1 ст+k - k А  ,    ^{C q ( — 1) n} _pCT+k ,      ^{( — 1) n}        ст _{= 0}

⁺ ... ⁺ (m — 1) ²(n - 1) V^{Qp    + a} 1 ^p      Г (m — 1) 2n ^{p   +} (m — 1) 2n+k cp    0'

Здесь a j , i = 1,... ,n , j = 1,... ,n, — соответствующие постоянные, которые зависят от а и а . Заметим, что а П = (onk) , a i =0 , i = 1,... ,n . Из последнего уравнения следует, что выполнена система

(-Т -а^п

(m-1)2n+k C ап an-1Cn-1 = —аП-1

^а П - 1 ^С п - 1 ^{+ а П} - 2 ^С п - 2 = ^—a n - 2

n-1         n-2               1              n aQ  Cn-1 + aQ Cn-2 + ... + aQC1 + cq — —aQ

Очевидно, что она имеет единственное решение. Отсюда следует, что можно выбрать nk константы c, ci, i = 0,... ,n — 1, так, чтобы функция u(p) = pCTe a/p была решением уравнения (17). Решение (14) является обратным преобразованием Лапласа — Бореля этой функции. Найдем все асимптотики его решений. Разделим это уравнение на rn(m-1) и запишем его в виде n + k k(m — 1)

_ n(m-i) d \ ^{n +k} n + k ___ 1

u

‘ n + k

^{+ c} n^-1 k(m — 1)

m -

n ( m - i) n + k

- 1

—

n + k k ( m — 1)

k+n - 1

,- n(m-1) d \ n+k dr) u

^{+ c} n - 2

П + k \ ² 2 ^ m - nm -d ) - 1 ) / П + k k(m — 1) J                 \ k(m — 1)

n ^{( m -i)} d \

■^m    n + k --- 1

k+n - 2

u

‘ / n + k n^{n +} ... ^{+ c} 1 Um—i ))

_r (n - 1) (m - nn+k) - 1) Л    n ^{+ k}

\ k(m — 1)

m - ' m_; d \ k⁺¹

Г      n + k -- I u

‘ / n + k V _n ( m- ^m-k - 1 ) I n + k    m- ⁿ (m ^-1 ) d\^k / n + k \^n+k

^{+ c} Q Um—n ) ^r          (— dm—d^r      dr) ^{u +} '^:k. . ) ^u = ⁰

/     . , \n+k где c = (—1)n+1(m — 1)2n+kаП =

Здесь основной символ H q

₌ „n+k ,       ^n+k ]

p ⁺ c

( - 1) ⁿ⁺¹ (m — 1) ²ⁿ⁺k ( ok ) n , a c i , i = 0,... ,n — 1, — соответствующие константы.

Отсюда следует, что

H q = p n^+k + ( — 1) ⁿ⁺¹ (m — 1) ^2n+k (— V (—n+k— V^+k nJ km^m — 1)

= p ^n+k + ( — 1) ⁿ⁺¹ (m — 1) ⁿ

Из теоремы 1 видно, что если к + 1 = mn, m G N, к G N, m > к, асимптотика решения удовлетворяет соотношению n+k /           mk+n-1     j \^

• u ~ E exP I Ej , + E          L^j E bjri' >

imk^+n                           imk^+n i

• j=1     \r k         i=1 r + J

Замечание. Уравнение (17) может быть приведено к виду

J n i । k d \ⁿ         _k          (n - i)k /iik d\      . (n-2)k J ,,k d \²

I — ^p ⁺ n d— \ u + b Q p u + b 1 p n i p ⁺ n d~ j u + b 1 P ⁿ \P ⁿ dp j u

• + ... + b n-1 p n fp ¹⁺nУ V ⁺ ( n ) у---- Ln +k ^cu = 0

\    dp J      kkJ (m — 1) ^2n+k

Здесь через b i , i = 0,...,n — 1, обозначены соответствующие константы. Основной символ оператора равен qⁿ + (n)n ( _{m -} 1) _2n+k , c . Он имеет простые корни а 1 ,..., a n . Отсюда следует, что асимптотики уравнения (19) представимы в виде линейной комбинации функций u j , j = 1,..., n :

u j

exp

(k-n-1     j aj + E ai k                    k-i pn     i=1 p~

)м pσj     bijpi .

i=Q

Отсюда следует, что B_k /n u j представимо в виде (18).

Вернемся к рассмотрению примера (3). Найдем

B ₂ ¹ exp

2 Vc ГТ

I' p 2

∞

E biPi- i=Q

Так как в этом случае к = 3 , n = 2 , m = 2 , то из формулы (13) следует, что

± 2 V C

B ^- exp -23- pP ^b i p i p ²       i=Q

^E    (^a j

X exp — j=1     v⁵

mk+n - 1 j \ ^M

+ E i г ^а ^ Ebj r.

i=1 ^{r 5} /      i=Q

Коэффициенты a j , j = 1, 2,..., 5, определяются из теоремы, а именно они являются корнями многочлена p ⁵ — ( | } ⁵ .

Отсюда следует, что асимптотики решения уравнения (3) имеет вид (18).

Таким образом, результат теоремы 2 расширяет возможность применения метода повторного квантования к дифференциальным уравнениям, образы Лапласа — Бореля которых являются уравнениями с дробными порядками вырождения и основными символами имеющими простые корни.