Применение метода проекции градиента к численному решению трехмерной задачи Стокса

Численное моделирование трехмерных стоксовых (ползущих) течений со свободной границей, помимо многочисленных практических приложений (например, моделирование трехмерной конвекции в мантии Земли [1–3]), является одной из важных исследовательских проблем гидродинамики при малых числах Рейнольдса. В настоящее время разработан ряд численных алгоритмов ее решения [4–6].

При рассмотрении задачи в переменных «скорость–давление» [1, 2]) неизбежно возникают следующие трудности:

• •    так как условие несжимаемости заменяется на слабую сжимаемость, при численной реализации это может привести к появлению дополнительной погрешности, особенно в задачах со свободной границей [7];

• •    для определения давления необходимо решать неоднородную задачу Неймана [1], численное решение которой методом установления (например, попеременнотреугольным методом в трехслойной модификации с выбором итерационных параметров по методу сопряженных градиентов, используемым в [8]) имеет очень слабую сходимость даже в двухмерном варианте [5];

• •    применяемый в [2] для решения задачи метод расщепления по физическим процессам [8], существенно увеличивает размерность системы разностных уравнений, поскольку предполагает совместное решение задач для скорости и давления, а также имеет слабую сходимость и низкую точность на свободной границе и границах разрыва вязкости.

При решении трехмерных задач гидродинамики достаточно хорошо зарекомендовал себя метод решения в переменных «завихренность–векторный потенциал» [5, 3, 9]. Несмотря на то, что в этом случае условие несжимаемости выполняется точно, возникается ряд дополнительных проблем:

• •    значительно увеличивается размерность вычислительной задачи, поскольку необходимо решать не три, а шесть уравнений для векторного потенциала и завихренности;

• •    векторный потенциал, в свою очередь, должен удовлетворять условию несжимаемости: только в этом случае задача сводится к решению шести простых уравнений Пуассона, однако в разработанных алгоритмах условие несжимаемости выполняется лишь на непроницаемой границе и не используются какие-либо специальные процедуры для достижения его точного выполнения в остальных точках расчетной области;

• •    данный метод не очень удобен для задач со свободной границей из-за трудности задания граничных условий: они получаются очень громоздкими, содержащими производные третьего порядка от искомых функций.

2.    Система уравнений. Вариационная постановка задачи

В настоящей работе осуществляется развитие на трехмерный случай эффективного численного подхода к решению задачи Стокса [12], который обладает преимуществами традиционных методов решения в переменных «векторный потенциал–завихренность» и «скорость–давление».

В поле силы тяжести рассмотрим трехмерную область D с границей Г , заполненную вязкой несжимаемой жидкостью. Медленное (ползущее) течение с переменной вязкостью и плотностью описывается уравнениями движения вязкой жидкости в приближении Стокса [4, 11]:

• -V p + 2V-(p defu )-р g = 0, (1)

• V- u = 0, (2)

где I — единичный тензор; g — ускорение силы тяжести; ц — коэффициент вязкости жидкости; р — плотность жидкости; u — вектор скорости; p — давление;

defu — тензор скоростей деформации. Если обозначить через ui компоненты скорости, то компоненты

def u равны 2 ( и j + u j i ) , где

( i , j = 1,3 ) .

Пусть Г состоит из двух частей: Г = Г1 иГ2. На части Г1 зададим условие полного прилипания u = 0

или гладкого контакта u • n = 0,(4)

а на Г 2 — условие на подвижной границе:

(-pI + 2цdefu)• n = f .(5)

f — вектор внешней нагрузки; n — нормаль к соответствующей границе.

Если существуют внутренние границы разрыва вязкости и/или плотности, на них задаются условия непрерывности скоростей и напряжений:

[ u ] - = 0,      [ - p I + 2 ц def u ] - • n = 0 ,

где [ - p I + 2 ц def u ] - — это скачок функции на границе.

Уравнения системы (1) , (2) и граничные условия (3)– (6) позволяют записать основное интегральное тождество (принцип виртуальных работ) [11]:

J ( u , v ) = C ( u , v ) - P ( v ) - F ( v ) = 0,

где v — произвольное трехмерное векторное поле;

C ( u , v ) = 2 JJJ ц def u def v dx 1 dx ₂ dx 3 —

D мощность внутренних напряжений;

P ( v ) = JjJ p V • v dx 1 dx ₂ dx 3

— работа, совершаемая

D

давлением;

F ( v ) = JJ f • v dS - JJJ p g • v dx 1 dx ₂ dx 3

— работа внешних поверхностных и

Г2              D массовых сил.

Так как C ( u , v ) — симметричный и положительно определенный оператор, то решение краевой задачи (1) , (2) существует и единственно [6]. Если перейти к эквивалентной задаче минимизации, искомое решение является минимумом функционала [ J ( u , u ) - F ( u ) ] на пространстве соленоидальных функций.

3.    Описание метода

Численное решение задачи Стокса определялось методом конечных элементов [6, 11]. Приближенное решение находилось в виде:

N

U = £ U Ч ,                                                (8)

k =1

где U ^k — узловые значения; ф _k — система базисных функций.

Для решения конечноэлементной задачи, получающейся в результате дискретизации функционала (7) , воспользуемся модифицированным методом проекции градиента, который позволяет исключить часть компонент узловых значений скорости

U k путем введения дискретного аналога функции тока [12]. Простой перенос этого метода на трехмерный вариант невозможен, но, как будет показано ниже, и в этом случае удается найти экономичную процедуру исключения.

Решим задачу на примере прямоугольного параллепипеда П = [ 0, X 1 ]^х[ 0, X ₂ ] х [ 0, X ₃ ] , который с помощью одномерных сеток разобъем на частичные параллепипеды. Рассмотрим произвольный элемент разбиения, который обозначим через d . В качестве базисных используем функции, имеющие форму тензорного произведения квадратичных одномерных лагранжевых элементов: Ф k ( x 1 ,x ₂, x ₃ ) = L₂ ( x 1 ) L k ( x ₂ ) L₂ ( x ₃ ) [11]. В этом случае каждый элемент содержит 27 узлов, которые расположены в вершинах d , на серединах ребер и в центре (Рис 1).

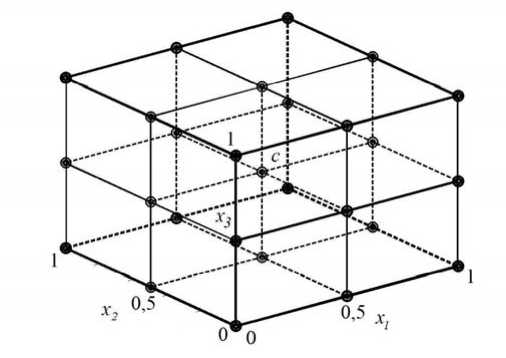
Рис. 1. Трехмерный прямоугольный элемент с 27 узлами

Используя метод, аналогичный [6], можно исключить компоненты скорости во внутреннем узле элемента, одновременно улучшив аппроксимацию давления. Аппроксимируем давление кусочно-непрерыной функцией, линейной на каждом элементе: P = p ₀ + p_ix_i, i = 1,3. В качестве v выберем векторное пространство,

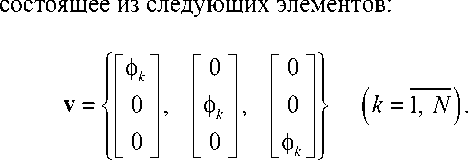
Подставляя (8) и (9) в (7) , получим следующую конечноэлементную задачу:

J ( u , v ) = C ( U , v ) - ^ p ₀ JJJ V- U dx 1 dx ₂ dx₃ - ^ p j JJJ x j V- U dx dx ₂ dx₃ - F ( v ) = 0.   (10)

k = 1       d                            k = 1       d

Тогда дискретный аналог условия несжимаемости, которому должны удовлетворять U ^k , примет вид:

JJJ V- U dx₁ dx ₂ dx ₃ = 0, d

JJJ x i V " U dx₁ dx ₂ dx ₃ = 0

( i = 1, 3 ) .

d

Преобразуем второй интеграл в (11) , используя формулу Остроградского-Гаусса:

∫∫∫ x_i ∇⋅ U dx ₁ dx ₂ dx ₃ = ∑∫∫ dm = 1 S_m

x

U ⋅ n dS -

∫∫∫ U_idx ₁ dx ₂ dx ₃ = 0, d

где S_m — грани элемента d ; n — нормаль к грани.

Для удобства перепишем (12) следующим образом:

6 ∫∫∫ x_i ∇⋅ U dx ₁ dx ₂ dx ₃ = ∑∫∫

d

m

x_i U ⋅ n dS - ∑ U ^j ∫∫∫ φ _jdx ₁ dx ₂ dx ₃ j ≠ cd

- U ^c ∫∫∫ φ _cdx ₁ dx ₂ dx ₃ = 0, (13) d

где c — центральный узел элемента d . Базисные функции узла c равны нулю на границе d , следовательно, значения скоростей U ^c не входят в поверхностный интеграл, и уравнения (12) можно решить относительно этих значений, а затем исключить их из задачи (10) , не нарушая разреженную структуру матрицы жесткости.

Теперь преобразуем первый интеграл из (11) по формуле Остроградского-Гаусса: