Применение метода Прони для анализа выходных сигналов преобразователей давления

Задача применения метода Прони для анализа выходных сигналов преобразователей давления может быть сформулирована следующим образом: необходимо оценить значения частот в выходном сигнале преобразователя с точностью, достаточной для того, чтобы проводить диагностику сенсора по изменению значения частоты. Предварительное моделирование показало, что значения частот необходимо определять с точностью до третьего знака (0,1 %). 2

Для решения данной задачи необходимо исследовать пределы точности, с которой метод Прони позволяет оценивать частоты, содержащиеся в сигнале отклика тензопреобразователя в зависимости от параметров сигнала (уровня сиг-нал/шум, частоты дискретизации, количества частот в сигнале, взаимной близости частот) и параметров самого метода (количества анализируемых отсчетов, порядка модели и предполагаемого числа частот, других параметров, введенных для уменьшения влияния шума).

Стандартная процедура Прони предполагает следующие основные этапы [4]:

• 1.    Определение параметров (коэффициентов) линейного предсказания, с помощью которых осуществляется подгонка имеющихся данных.

• 2.    Формирование из найденных коэффициентов линейного предсказания характеристического полинома и определение его корней.

• 3.    Оценка по корням полинома частот и коэффициентов затухания синусоид для каждого экспоненциального члена.

• 4.    Оценка амплитуд экспонент и начальных фаз синусоид путем решения системы линейных уравнений (если эти оценки необходимы).

Для упрощения идентификации экспоненциальных сигналов на фоне шума и улучшения точности оценок затухания и частоты применяют следующие приемы:

• 1.    Выбор завышенного порядка модели сигнала (количества экспонент).

• 2.    Разложение матриц Тёплица, участвующих в вычислениях коэффициентов, по сингулярным числам.

• 3.    Использование коэффициентов и нулей полинома линейного предсказания вперед и назад.

В методе присутствует ряд параметров, значения которых влияют на точность определения частоты. Соответственно, необходимо исследование влияния данных параметров на точность метода и, если это возможно, предложить алгоритм подбора их оптимальных значений.

Параметры метода таковы:

• 1.    Количество анализируемых отсчетов N . В принципе может быть как минимум в два раза больше числа экспонент в сигнале (в случае затухающих синусоид на каждую частоту приходится по две комплексно сопряженные экспоненты). Вероятно, увеличение количества отсчетов улучшает результат.

• 2.    Порядок модели p и предполагаемое число q экспонент. Для случая сигнала без шума лучшим является точное указание количества экспонент. В случае наличия шума полезным является завышенное значение p . Это добавляет дополнительные ложные корни, не связанные с частотами сигнала, но в то же время дает более точные оценки имеющихся реальных частот. Предполагаемое число экспонент используется при сингулярном разложении матрицы Тёплица для улучшения вектора данных и уменьшения влияния шума.

• 3.    Другие параметры, вводимые для устранения шума. В качестве примера может служить «радиус зоны обнаружения», введенный в [5], связанный с отделением реальных и ложных корней полинома при использовании коэффициентов линейного предсказания вперед и назад.

Помимо параметров самого метода, на точность оценки оказывают влияние параметры сиг- нала, такие как уровень шума, количество синусоид, их взаимная близость и т. п. Параметры сигнала таковы:

• 1.    Частота дискретизации Fs сигнала. В принципе этот параметр можно регулировать. Скорее этот параметр относится к параметрам обработки сигнала, но, так или иначе, он все же связан с отсчетами, которые только затем подвергаются обработке методом Прони. Частота дискретизации влияет на вычисление частоты и коэффициента затухания, так как входит в качестве размерного коэффициента в расчетные формулы. В работе [6] предложен алгоритм вычисления оптимальной частоты дискретизации для n частот.

• 2.    Отношение сигнал/шум SNR. Определяется как отношение полезного сигнала к уровню шума. В случае модельного сигнала его вычисление не представляет особенных трудностей. В случае реального сигнала необходимо дополнительно предлагать методику оценки данного соотношения. Предлагается в качестве SNR выбрать следующую величину [5]:

• 3.    Количество L синусоид, присутствующих в сигнале. Им соответствует 2* L экспонент. Этим числом определяется порядок модели. В случае реального сигнала, как правило, неизвестно.

• 4.    Взаимная близость синусоид A f= f l - f2| или 3f = fl - f 2 \/f1.

SNR= 10*log 10 (sum( S .^2)/(sigma*sigma* N )) , где S – значения отсчетов полезной части сигнала; sigma – среднеквадратическое отклонение (СКО) шума; N – количество отсчетов. Лучше, если значение SNR будет рассчитано для каждого обрабатываемого отрезка сигнала.

В качестве примера того, как частота дискретизации сигнала может влиять на точность оценки частоты, на рисунке приведены восстановленные и смоделированные зашумленные сигналы, содержащие три частоты. Из рисунка видно, что наилучшее восстановление сигнала получается при частоте дискретизации, близкой к оптимальной (в данном случае – 3800 Гц).

Оптимальную частоту дискретизации сигнала для улучшения оценки при спектральном анализе методом Прони в случае n частот f 1 < f 2 < … < f_n можно вычислить по формуле

n

∑ f k ²

Fs - 4 n--- k ^- ------.

n

2 (2 k " 1) fk k-I

Дополнительное улучшение работоспособности метода Прони может дать использование методики разделения сигнала на частотные зоны с помощью вейвлет-преобразования или полосовой фильтрации.

Применение метода Прони для анализа выходных сигналов преобразователей давления

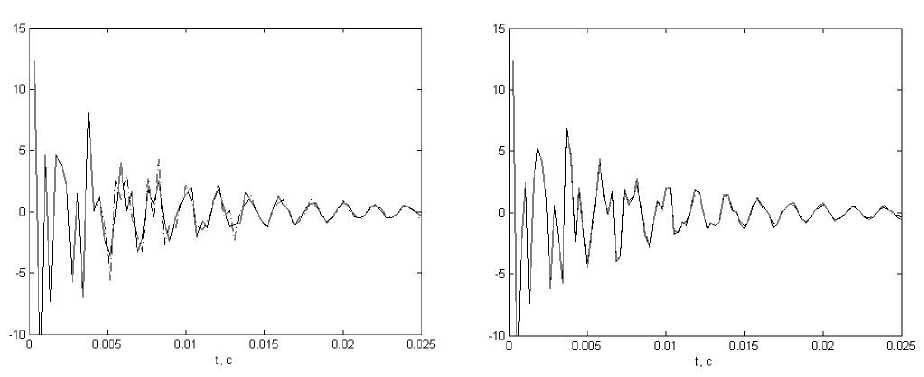
а)                                                                       б)

Зашумленный сигнал (сплошная линия) и его реконструкция (штриховая): а) при частоте дискретизации 2900 Гц; б) при частоте дискретизации 3800 Гц