Применение метода встречных прогонок для синтеза параллельного алгоритма решения сеточных уравнений трехдиагонального вида

Моделирование физических процессов посредством численного решения дифференциальных уравнений находит все более широкое применение в различных отраслях науки. Этому способствует развитие вычислительной техники и численных методов, ориентированных на решение таких уравнений. Наиболее распространенные методы (конечных разностей и Галеркина) сводят дифференциальную задачу к системе линейных алгебраических уравнений (СЛАУ) вида Ax=b, где матрица A - ленточная. К прямым методам решения такой системы относят различные варианты прогонки и редукции. С появлением вычислительных систем, реализующих параллельные вычисления, связано создание парал-лельнНистояо[|яятигать(ясн[оввя[иы1ианпаспроеииюдак.ис- следованию параллельных алгоритмов, ориентированных на кластерную архитектуру ЭВМ и основанных на методе встречных прогонок для решения сеточных уравнений трехдиагонального вида. Известно несколько параллельных алгоритмов, основанных на методе трехдиагональной прогонки. В [1] представлен алгоритм, использующий распределение матрицы системы между задачами (в терминах модели канал/задача [2]), позволяющее каждой задаче алгоритма решать свою подсистему, выражая решение через значения на границах области данных, входящих в задачу. Для вычислительных систем с различной архитектурой синтезировано целое семейство параллельных алгоритмов, основанных на этом принципе. Недостатком такого подхода является наличие глобальных коммуникаций, нежелательных для кластерной архитектуры. В [3] предложено решение поставленной задачи с использованием метода редукции, к сожалению также не свободное от глобальных коммуникаций. Принципиально другой подход содержится в [4]. Автор алгоритма отказался от идеи одновременного решения одной СЛАУ несколькими задачами, применив вместо декомпозиции данных функциональную декомпозицию. Все задачи алгоритма одновременно решают разные подсистемы разных СЛАУ, общаясь посредством локальных коммуникаций. Использование функциональной декомпозиции ограничивает область применения данного подхода, не позволяя решать одномерные задачи мате- матической физики. Другим недостатком алгоритма является неполная загруженность задач: на начальном и конечном этапах расчета часть задач не производит вычислений, ожидая получения необходимых данных. Вариант алгоритма, исключающий простои, требует передачи вдвое большего объема данных из-за неудачной декомпозиции сеточной области. Тем не менее, этот подход представляется наиболее перспективным. В данной работе он применяется к распараллеливанию метода встречных прогонок, что позволяет использовать его для решения одномерных задач математической физики, снизить вдвое время ожидания и улучшить декомпозицию сеточной области для варианта без простоев.

Описание параллельных алгоритмов

Алгоритм 1.

Рассмотрим простейший алгоритм, состоящий из двух задач. Функциональная декомпозиция задается спецификой метода встречных прогонок, в котором прогоночные коэффициенты ( а , в и n , Z ) вычисляются с двух сторон по направлению к центру матрицы А [5]. В последовательном алгоритме этот прием используется, когда желают ограничиться нахождением не всего вектора х, а лишь его части. Так как вычисления двух пар коэффициентов прогонки независимы (информационно, логически и конку-ренционно), то их можно осуществлять параллельно. Произведем разбиение одномерной сеточной области ю1 на ю1 и ю² (рис. 1). Вычисления разделим на три этапа, соответствующие прямому (рис. 1 а), обратному ходу (рис.1 в) встречных прогонок и обмену данными между задачами (рис. 1 б).

Во время прямого хода прогонок первая задача находит прогоночные коэффициенты а , в , вторая задача n , Z . На этом этапе алгоритма (как и на остальных этапах) задачи производят независимые вычисления, следовательно, могут исполняться параллельно. Далее, первая задача передает второй пару чисел а , в , необходимых для запуска обратного хода прогонки во второй задаче, которая в это время производит аналогичную передачу, необходимую первой задаче. На третьем этапе обе задачи одновременно реализуют обратный ход прогонок, находя решение

СЛАУ. Ускорение такого алгоритма можно оценить как:

k =     ^T a ( ^N )

S Ta (N)+ 24 ’ где N - размерность СЛАУ, та(N)=3Nтх+(2N+1)т+3Nt+ - время расчета по последовательному алгоритму (т+ - длительность одной операции сложения (вычитание понимаем как сложение), тх - длительность одной операции умножения, т^ - длительность одной операции деления), т к -время передачи или приема (считаем их равными) одного пакета по сети. При пакетной передаче данных время передачи разного объема информации будет оставаться константой до тех пор, пока объем передаваемого массива не превысит размер пакета. Здесь, и в дальнейшем, это условие соблюдается.

задача 1          задача 2

б)

а)

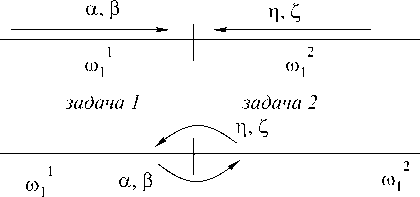
задача 1

задача 2

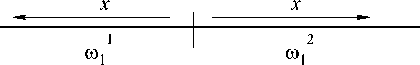
Рис. 1. Этапы вычислений по параллельному алгоритму, состоящему из двух задач и реализующему метод встречных прогонок для одной СЛАУ а - прямой ход прогонок; б - обмен данными между задачами; в - обратный ход прогонок

Очевидно, при N -^« k ^ 2. К сожалению, этот подход нельзя развить для большего количества задач, если сеточная область ю одномерна. Функциональная декомпозиция, как правило, ограничивает масштабируемость алгоритма. В нашем случае, алгоритм 1 не обладает свойством масштабируемости [2].

Алгоритм 2.

Для двумерной области ю ₂ это ограничение снимается. Применительно к ней будем говорить о прогонке по строкам (продольной прогонке) и столбцам (поперечной прогонке) сеточной области, как это принято в методах расщепления и переменных направлений [6].

Если алгоритм состоит из двух задач, то модификации, по сравнению с предыдущим алгоритмом, не требуется, каждая СЛАУ в продольном направлении решается одновременно двумя задачами. Ускорения такого алгоритма и известного алгоритма из [4] составят k =   2 Nt a (N)

2  Nt a (N)+ 2 NTk n ~~ _         2 Nt a (N)

и к 2   1.

^{N T} a ^{( N )+ 2} N ^T k ⁺ ^ ^T a ^{( N} )

Третье слагаемое в знаменателе последней формулы есть время ожидания для задачи в стандартном алгоритме. Сформулированный выше вариант алгоритма лишен ожиданий.

Для алгоритма из четырех задач производится следующее разбиение сеточной области (рис. 2).

На рис. 2 (а-в) представлены начальные этапы вычислений по алгоритму. Задачи 1, 4 (рис. 2 а) начинают прямой ход прогонок для строки 1 и передают прогоночные коэффициенты задачам 2, 3, кото- рые на первом этапе простаивают.

Далее не будем специально говорить об обмене данными между задачами, подразумевая, что перед прямым ходом они принимают прогоночные коэффициенты, после прямого хода передают их. Перед обратным ходом принимают значение сеточной функции, после - передают его. Первая и последняя задачи начинают прямой ход без принятия прогоночных коэффициентов, а задачи под номерами L /2 и L /2+1 ( L - общее число задач) начинают обратный ход принятием прогоночных коэффициентов (друг от друга).

На втором этапе (рис. 2 б) задачи 2, 3 продолжают прямой ход для строки 1, задачи 1, 4 начинают прямой ход для строки 2. Третий этап (рис. 2 в) характеризуется простоем задач 1,4 и началом обратного хода прогонок для строки 1 задачами 2,3. Четвертый этап (рис. 2 г) - прямой ход, задачи 1, 4 осуществляют его для строки 3, задачи 2,3 для строки 2. Пятый этап (рис. 2 д) - обратный ход, задачи 1, 4 осуществляют его для строки 2, задачи 2, 3 для строки 3. Далее прямой и обратный ходы чередуются, пока задачи 2, 3 не произведут прямой ход прогонок для последней строки. На следующем этапе задачи 1,4 будут простаивать, задачи 2,3 начнут обратный ход. Заключительный этап алгоритма характеризуется простоем задач 2, 3, в то время, как задачи 1,4 завершат обратный ход прогонок для последней строки сеточной области. Прогонка по столбцам осуществляется каждой задачей самостоятельно, эти вычисления независимы. Пусть размер сеточной области ю2 - NxN точек, тогда ускорение данного алгоритма и ускорение стандартного алгоритма оценим величинами k =          2 NTa (N)

• ⁴  /4N ^T a ^{( N )+ 4 N T} k ⁺ 14 ^T a ^{( N} )

  ~

  и k ₄

  
  

N ² T a ( N )

12 NTa (N) + 4NTk + 34 Ta (N) + 4Tk где 14 т а(N - время ожидания в разработанном алгоритме, 31 т а(N)+4t к - время ожидания в извест- ном алгоритме.

задачи 12   34

1 2 3 а)		*	*
	1 со2	2 Ю2	3 оэ2	4 Ю2
	задачи 12   34
1 2 3 б)
	1 (1)2	2 Ю2	3 со2	4 со2
	задачи 12   34
1 2 3 в)	*			*
	1 со2	2 со2	3 со2	4 со2
	задачи 12     3     4
1 2 3 г)
	1 со2	2 со2	3 Ю2	4 со2
	задачи 12   34
1 2 3 д)
	1 со2	2 М2	3 оэ2	4 со2

Рис. 2. Этапы вычислений по параллельному алгоритму, состоящему из четырех задач, для прогонки по строкам на а2. а, б,г - прямой ход прогонок; в,д - обратный ход прогонок. Задача, помеченная символом «*», простаивает k четн.

~

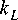
______________ 2 N T a ( N ) ______________ 2 N T a ( N ) + 4 N T k + ^ T a ( N ) + ( L - 4) T k

_________________2NTa (N)_________________

2N T a ( N ) + 4 NT k + ^ LL —) T a ( N) + 2( L - 2)T_k

Время ожидания снижено более чем вдвое по сравнению со стандартным алгоритмом, остальные характеристики одинаковы. Следовательно, ускорение разработанного алгоритма превышает ускорение ранее известного алгоритма. В случае, когда алгоритм из двух задач производит вычисления на области, содержащей две строки, время вычислений сократится в полтора раза.

Для алгоритма с нечетным числом задач результат сравнения окажется скромнее. Поделим область to ₂ так, как это показано на рис. 3.

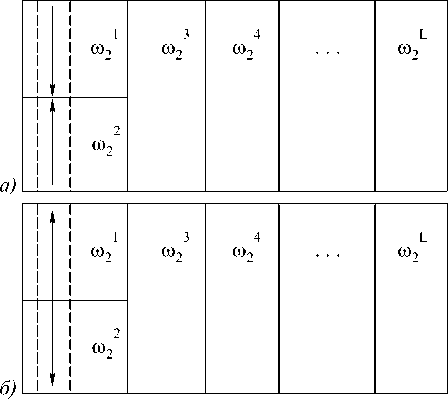
Рис. 3. Этапы вычислений по параллельному алгоритму, состоящему из нечетного числа задач, для прогонки по столбцам. а - прямой ход прогонки;

б - обратный

Прогонка по строкам осуществляется так же, как при четном числе задач, ведь с каждой строкой работает L -1 задача. Появляется необходимость в распараллеливании прогонки по столбцам между двумя первыми задачами (рис.3). При реализации этой прогонки время коммуникаций увеличивается по сравнению с алгоритмом для четного числа задач.

Алгоритм 3.

Осуществим двумерную декомпозицию сеточной области ω 2 для построения параллельного алгоритма метода встречных прогонок. Очевидный вариант такой декомпозиции на четыре подобласти и этапы алгоритма представлены на рис. 4.

Очевидно развитие алгоритма для произвольного четного числа задач. Для L задач ускорения соста-

вят

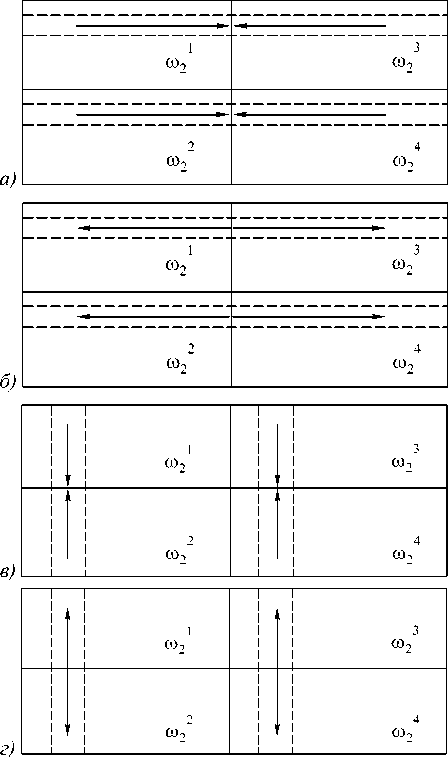
Рис. 4. Этапы вычислений по параллельному алгоритму, состоящему из четырех задач, с двумерной декомпозицией сеточной области. а -прямой ход прогонок по строкам, б - обратный ход прогонок по строкам, в - прямой ход прогонок по столбцам, г - обратный ход прогонок по столбцам.

Четырехзадачные алгоритмы с двумерной декомпозицией сеточной области (представленный на рис. 4 и известный) обеспечивают следующие ускорения , 2 D       2 N t a ( N )        ~ 2 D       2 N t a ( N )

^k 4   = i                         , ^k 4   = i                       ■

2 ^N 2^Ta ^{( N )+ 2} N ^T k         2_ N ^T a ^{( N )+ 6} N ^T k

В отличии от четырехзадачного алгоритма (как изложенного выше, так и из [4]) с одномерной декомпозицией ω2, алгоритм с двумерной декомпозицией не содержит простоев и оперирует вдвое меньшим объемом данных при установке коммуникаций между задачами. По сравнению с известным алгоритмом [4], использующим двумерную декомпозицию, алгоритм 3 тратит втрое меньше времени на коммуникации между задачами.

Декомпозиция области и действия по алгоритму из восьми задач иллюстрируются на рис. 5. Особенность разделения ω2 между задачами состоит в принадлежности одной задаче двух квадратных подобластей. Их взаимное расположение позволяет распараллеливать вычисления прогонки как по строкам, так и по столбцам области.

а)	1 Ю2       *'	2 оз2	6 co2	5 co2
	2 co2       *	(02	5 O32	6
	3 co2       *	4 оз2	8 co2	7 to2
	4 co2 -----	3 O32	7 O32	8 -*----- co2
б)	1 оз2	2 O32      *	6 *     O32	5 co2
	2 co2	1 O32 -----	5 co2	6 co2
	3 co2	4 co2        *■	8 O32	7 co2
	4 co2	3 оз2 -----*-	7 -*-----co2	8 co2

	1 co2	2 O32 *	6 * co2	5 co2
	2 co2	1 co2 -	5 • co2	6 co2
	3 co2	4 O32	8 (02	7 (132
в)	4 co2	3 to2 -—	7 ---- ™2	8
	1 cd2 *	2 оз2	6 оз2	5
	2 co2 *	1 co2	5 O32	6 • to2
	3 оз2	4 оз2	8 co2	7 co2
г)	4 co2 —----	3 co2	7 O32	8 ---- ™2

Рис. 5. Этапы вычислений прогонок по строкам

(восьмизадачный алгоритм с двумерной декомпозицией сеточной области).

а, б - прямой ход прогонок по строкам, в, г - обратный ход прогонок по строкам

На первом этапе алгоритма (рис. 5 а) производится прямой ход прогонок по строкам в левой и правой четвертях ω 2 . На втором этапе (рис. 5 б) прямой ход прогонок по строкам заканчивается, вычисления из левой четверти переносятся на одну подобласть вправо, из правой четверти на одну подобласть влево. Третий и четвертый этапы алгоритма (рис. 5 г, д) - обратный ход прогонок по строкам. Аналогично производятся прогонки по столбцам. Сравним ускорения описанного алгоритма и алгоритма с двумерной декомпозицией ω 2 из [4]

_K2 d_    2 N T a ( N )       ~ 2 D_    2 N T a ( N )

^k 8    = i                         , ^k 8     = i                         ■

4 N T a ( N )+ 3 N T k         4 N T a ( N )+ 7 N T k

Выигрыш по времени коммуникаций составляет 2,5 раза. По сравнению с алгоритмами, основанными на одномерной декомпозиции области, выигрыш по времени коммуникаций меньше (1,25 раза), за то отсутствуют простои, присущие этим алгорит- мам.

Двумерная декомпозиция ω2 при L=2q и q>3 производится аналогично разбиению на рис. 5. При этом ускорения разработанного и известного алго- ритмов составят k 2 d =         2 Nt a (N)

L    2 N t a ( N ) / L + 4(1 - 2/ L ) N т _k ’

N t a ( N )

2 N t a ( N ) / L + 8(1 - 1/ L ) N T k "

Выигрыш по времени коммуникаций оценивается величиной 2( L -1)/( L -2). По сравнению с алгоритмом 2 этот выигрыш окажется значительно 1

меньше и составит ^— 2/L^{, н0 п}Ри этом алгоритм 3

полностью лишен простоев.

Алгоритм 3 разработан для числа задач L - степени двойки. Является ли это ограничение существенным? Отметим локальность коммуникаций алгоритма 3. Каждая задача имеет log 2 L соседей, что соответствует степени связности гиперкуба с L вершинами. Вычисления по предложенному алгоритму разумно производить на ЭВМ с кластерной архитектурой, процессоры которой являются вершинами гиперкуба. Такая архитектура наиболее распространена в настоящее время, следовательно, ограничение алгоритма по числу задач несущественно.

Ранее, имея в своем распоряжении алгоритмы из [4], исследователь сталкивался с проблемой выбора декомпозиции сеточной области. Вариант с одномерной декомпозиции обеспечивал меньший объем коммуникаций, вариант с двумерной декомпозицией был свободен от простоев задач. Алгоритм 3, представленный в данной работе, для квадратной сеточной области обеспечивает, без простоев, наименьшее время коммуникации, по сравнению с известными параллельными алгоритмами из [4].

Численное исследование ускорения параллельных вычислительных процессов, порожденных разработанными алгоритмами

При аналитическом анализе ускорения параллельных алгоритмов сложно учесть все особенности конкретной вычислительной системы (работа с памятью, сетью и т.д.). Становится важным исследование ускорения параллельных вычислительных процессов (ПВП), порожденных синтезированными алгоритмами, позволяющее выявить ранее неучтенные эффекты, присущие практике параллельных вычислений. В дальнейшем, с учетом найденных закономерностей, можно повысить ускорение параллельного алгоритма, соответственно его модифицировав.

Изучим поведение ускорения s ПВП, порожденного алгоритмом 1, меняя размерность сеточной области (рис. 6). Все вычислительные эксперименты проводились на кластере из двух двухпроцессорных ЭВМ Pentium III, связанных сетью Mirinet.

При N =1000 (рис. 6 а) ускорение оказалось меньше 1, время вычислений по параллельному алгоритму больше времени вычислений по последовательному алгоритму.

Выясним, почему это происходит.

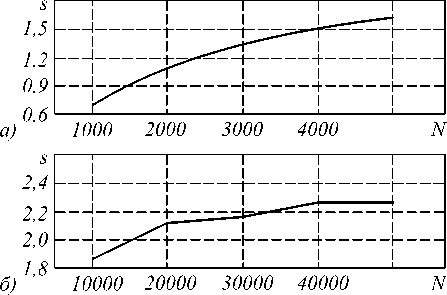
Рис. 6. Зависимость ускорения ПВП, порожденного алгоритмом 1, от размерности сеточной области, для разных диапазонов N

Длительность арифметических вычислений оценим величиной O(N), длительность коммуникаций - константа тк. Из определения функции «О большое» O(N)N' ускорение превысит 1 и по сравнению с последовательным вычислительным процессом получим ожидаемый выигрыш по времени (рис.6 а). Сверху ускорение ограничивается законом Амдала [2], по которому 1

• 5    <----------- , где q - отношение времени испол-

• q + (1 - q)/P

  нения части процесса, которую невозможно распараллелить, ко времени исполнения всего последовательного вычислительного процесса. Всегда найдется вычислительная операция, которую распараллелить нельзя, но, даже положив q=0, ускорение останется ограничено числом процессоров P вычислительной системы. Для исследуемого ПВП ускорение, согласно закону Амдала, не должно превышать 2. Однако, как следует из рис. 6б, при N=20000, s>2. Для изучения этого эффекта обратимся к табл.1.

Таблица 1

Зависимость объема оперативной памяти, занимаемой последовательным вычислительным процессом, от размерности ® 1

	Размерность сеточной области ( N /1000)
	1	2	3	4	5	10	20	30	40	50
Объем занимаемой оперативной	23,3	46,8	70,1	93,5	117,9	234,7	468,5	703,2	937,5	1171,7

| памяти (кБ)

Начиная с размерности N =2000 (именно с нее ускорение превышает 2), объем памяти, занимаемый последовательным вычислительным процессом, превышает кэш процессора (256кБ). Следовательно, последовательный и параллельный процессы оперируют областями памяти, характеризующимися разными скоростями доступа к данным. Область памяти, занимаемая последовательным процессом при N =50000, выходит за размеры кэша на 915,87 кБ, а для ПВП этот показатель равен 329,93 и сравним с объемом кэш. Логично предположить, что как только объем памяти, занимаемой вычислительным процессом (не важно каким именно: последовательным или параллельным), превысит кэш на несколько порядков, ускорение опять подчинится закону Амдала. Действительно, при N =2000000 и занимаемой памяти 45,78 мБ, 5 =1,9969.

Исследуем ускорение ПВП, порожденного двухзадачным алгоритмом 2. Предварительно модифицируем алгоритм, учитывая особенности пакетной передачи данных по сети. Выберем диапазон N таким, чтобы объем всех передаваемых данных не превышал объем пакета (рис. 7). Организуем обмен между задачами не парой прогоночных коэффициентов, относящихся к одной строке области ю ₂, а коэффициентами сразу всех строк. Тогда объем коммуникаций уменьшится в N раз по сравнению с алгоритмом 2 и ускорение модифицированного алгоритма достигнет величины

• 2 N t ( N )

• 1    вект .               a

• ²     " Nt a ( N )+ 2 т_к

Такой алгоритм назовем векторным, прежний алгоритм - скалярным.

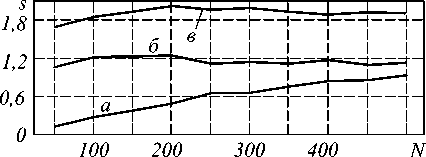
Рис. 7. Ускорения ПВП, порожденных алгоритмом 2.

а - ускорения для скалярного ПВП, б - для векторного ПВП, в - векторного ПВП, при соразмерном по занимаемой памяти последовательном вычислительном процессе

В исследуемом диапазоне значений N ускорение скалярного ПВП растет, не достигая 1. Ускорение векторного ПВП, как и ожидалось, превышает ускорение скалярного. При N =50 отношение

s

вект .

5 скал .

=7,19; при N =500

5 вект .

-----=1,22. Для выяснения

5 скал .

причины, по которой ускорение векторного ПВП не достигает предельного значения, установленного законом Амдала, опять обратимся к анализу объема оперативной памяти, занимаемой процессами. За уменьшение объема передаваемых данных приходиться платить увеличением используемой области памяти. Если одна задача скалярного алгоритма хранит N2+2N чисел, то одна задача векторного алгоритма - 3N2. Ветвь векторного ПВП уже при N=150 занимает 263,67 кБ, что превышает кэш. При такой размерности ускорение равно 1,22. С увеличением N ускорение векторного ПВП не возрастает. Это не соответствует аналитической зависимости ускорения алгоритма от размерности задачи. Из-за увеличения времени доступа к памяти при исполнении ПВП, по сравнению с последовательным вычислительным процессом, векторный алгоритм имеет смысл только при N<150 (разумеется, для данной вычислительной системы), что серьезно ограничивает область его применения. Для подтверждения предположения о влиянии объема занимаемой памяти на ускорение ПВП, используем при определении ускорения векторного ПВП длительность последовательного процесса, занимающего тот же объем памяти, что и векторный (рис. 7). Ускорение векторного ПВП, определенное таким образом, достигает теоретического предела.

В качестве компромисса между скалярным и векторным способами передачи данных выберем блочный способ. Ограничим размером блока M (M < N) количество строк, для которых прогоночные коэффициенты передаются в одном пакете. При этом часть пакета не будет заполнена полезной информацией, зато объем используемой памяти сократится до N 2 +2N x M . Произведение 2 N x M определяет объем памяти, отводящийся под прогоночные коэффициенты. На рис. 8 представлена зависимость ускорения блочного ПВП от M при N =500.

Применение блочного алгоритма позволило повысить ускорение с 5 =0,93 для скалярного ПВП и 5 =1,14 векторного ПВП до 5 =1,41 блочного ПВП (при М =40).

Автору не удалось аналитически выразить зависимость 5(M) , поэтому, рекомендую поиск оптимального М производить экспериментально. Например, при разностном решении дифференциального уравнения параболического типа, следует, ограничившись несколькими шагами по времени, подобрать оптимальную величину М , для которой, затем, произвести необходимые расчеты по решению разностного уравнения с требуемым числом шагов по времени.

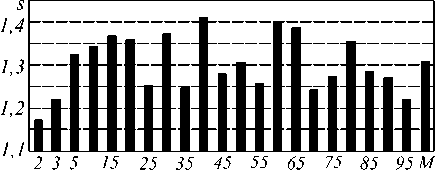
Рис. 8. Зависимость ускорения блочного ПВП от количества строк, для которых прогоночные коэффициенты передаются в одном пакете

При исследовании зависимости s(N) вышеизложенный подход применять нецелесообразно в силу большой трудоемкости. Для каждого значения N придется с помощью серии вычислительных экспериментов подбирать оптимальный размер блока, варьируя M в пределах от 1 до N , производя постановку N x K вычислительных экспериментов для определения вида зависимости s(N) по К отсчетам. На рис. 9 представлена зависимость ускорения блочного ПВП от размерности сеточной области ю ₂ для таких M , при которых объем памяти, занимаемой прогоночными коэффициентами, не выходит за пределы кэша (для M +1 это условие уже не соблюдается). Такой подход к выбору величины М представляется автору наиболее разумным, если экспериментальное исследование зависимости s(М) затруднено.

При нем ускорение должно оставаться постоянной величиной, ведь отношение времени арифметических операций ко времени вычислений, с увеличением N (до тех пор, пока объем передаваемых по сети данных не превзойдет объем пакета), не изменяется. Как видно из рис. 9, ускорение блочного ПВП можно считать постоянным и равным 1,4. Возможно, экспериментально исследуя s(M) при N =4000, удастся существенно повысить ускорение блочного ПВП, однако в этом нет необходимости. При возрастании N ускорение скалярного ПВП стремится к пределу, установленному законом Амдала (рис. 9). Для любой строки ю ₂ с увеличением размерности области, время коммуникаций остается постоянным, а длительность выполнения арифметиче-

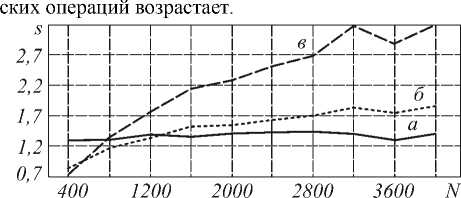
Рис. 9. Зависимость ускорения ПВП от размерности сеточной области.

Кривая а - зависимость для блочного ПВП, порожденного двухзадачным алгоритмом 2, б - для скалярного, порожденного двухзадачным алгоритмом 2, кривая в - для скалярного ПВП, порожденного четырехзадачным алгоритмом 3

Следовательно, для значений NN' - скалярный. Не следует полагать, что при небольших значениях N организация параллельных вычислений неуместна в виду малого размера сеточной области. Решая параболическое уравнение на сетке, содержащей число отсчетов по времени, превосходящее N на несколько порядков, при малой размерности ®2, можно столкнуться с си- туацией, когда время работы последовательной программы окажется неприемлемо большим. Тогда, даже для N=50, следует обратиться к параллельному алгоритму. Так как при малых N блочный алгоритм предпочтительнее скалярного, то в таких ситуациях разумнее использовать именно его.

Отметим, что все известные алгоритмы из [4] подразумевают использование бо льших объемов памяти, чем сформулированные здесь алгоритмы, которые и в этом смысле оказываются предпочтительнее.

Подтвердим экспериментально, что скалярный ПВП, порожденный четырехзадачным алгоритмом 3, развивает ускорение, превышающее единицу. Уже для N =800 (рис. 9) его ускорение выше, чем у скалярного и векторного ПВП, порожденных двухза-дачным алгоритмом 2. При N =7200 исследуемый ПВП достигает предельного ускорения (рис.10).

Для алгоритма 3 имеет смысл та же блочная модификация, что и для алгоритма 2.

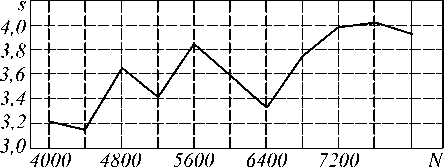
Рис. 10. Зависимость ускорения ПВП, порожденного четырехзадачным алгоритмом 3, от размерности сеточной области N

Выводы

В работе сформулированы параллельные алгоритмы для решения СЛАУ трехдиагонального вида методом встречных прогонок. Выбран оптимальный среди известных и представленных в настоящей работе алгоритмов с локальными коммуникациями между задачами. Предусматривая пересылку меньшего количества данных, будучи избавленным от простоев и требуя меньший объем памяти, он обеспечивает максимальное ускорение. Представлена экспериментальная методика, позволяющая повысить ускорение ПВП, используя блочную структуру коммуникаций.

Автор благодарит Владимира Александровича Шустова за помощь в интерпретации результатов вычислительных экспериментов.