Применение методов машинного обучения для настройки параметров технологического процесса электронно-лучевой сварки

DOI:

Главными целями развития в области машиностроения, авиации и космонавтике, энергетики и приборостроении является достижение высоких показателей качества, надежности и долговечности деталей, а также соединительных конструкций. К сварочным соединениям предъявляются наиболее высокие требования, удовлетворить которые способны современные и прогрессивные технологии сварки деталей

Одной из таких перспективных технологий является электронно-лучевая сварка (ЭЛС), которая дает возможность варьировать комбинации материалов для соединения, не смотря на природу этих материалов (включая использование растворимых и нерастворимых друг в друге материалов) [1]. Причиной, по которой ЭЛС выигрывает на фоне других технологий сварки, является минимальный диаметр пятна нагрева, иногда достигающий тысячных долей миллиметра. Такое преимущество позволяет технологам сваривать металлы очень маленькой толщины друг с другом [1].

Широкие возможности применения ЭЛС доказаны большим количеством научных исследований по оптимизации и моделированию процесса ЭЛС [2-5]. Дальнейшей тенденцией развития ЭЛС, на которой необходимо заострить внимание в рамках темы, является создание математических прогностических моделей технологического процесса сварки. При заранее заданных входных параметрах сварки необходимо делать предсказание размеров шва, что позволит повысить точность и качества соединительных конструкций [1].

ОПИСАНИЕ ПРОЦЕССА ЭЛС

ЭЛС - метод сварки, в основе которого лежит применение луча. Луч выделяет тепло, которое формируется в результате столкновения пучка заряженных частиц. Плотность энергии в таком луче высока, но ее недостаточно для качественной сварки.

Чтобы исправить эту проблему электроны нужно сконцентрировать в магнитной линзе. Далее электроны, находясь в подвижном состоянии, фокусируются в плотный световой пучок и ударяются о деталь. За счет столкновения электроны тормозятся, и их энергия превращается в тепло [6].

Схема электронной пушки изображена на рисунке 1. В конструкции предусмотрена магнитная отклоняющая катушка, которая позволяет перемещать электронный луч по детали.

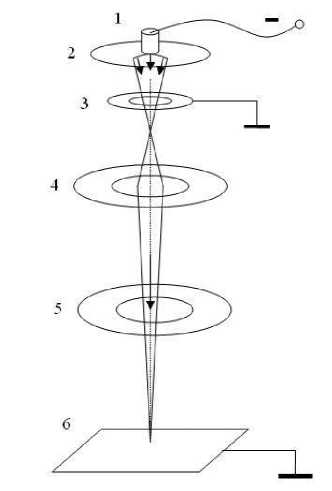
Рисунок 1. Электронная пушка: 1 - катод, 2 -электрод, 3 - анод, 4 - электромагнитная линза, 5 - отклоняющая катушка, 6 - свариваемое изделие.

Figure 1. Electron gun: 1 - cathode, 2 - electrode, 3 - anode, 4 - electromagnetic lens, 5 - deflecting coil, 6 - workpiece to be welded.

В пушке создают условия вакуума, так как они позволяют сохранить значительную часть кинетической энергии во время перемещения электронов к точке сварки.

Ключевыми математическими параметрами процесса ЭЛС, которые необходимы для создания модели прогнозирования, являются:

• •    величина сварочного тока, мА;

• •    ток фокусировки электронного луча, мА;

• •    расстояние от электронно-оптической системы до поверхности детали, мм;

• •    скорость перемещения луча по поверхности изделия, об/мин;

• •    ускоряющее напряжение, кВ.

ПРОБЛЕМАТИКА

Для любого технологического процесса существует проблема определения наиболее оптимальных параметров, позволяющих добиться требуемого уровня качества результата. В границах этой проблемы также может стоять формулировка поиска оптимальных параметрах в условии сохранения значений других, либо достигая минимального отклонения в значениях.

Как показывает опыт использования ЭЛС в производстве, процесс сварки относительно тяжело поддается настройке и не маловажную роль здесь играет дороговизна проведения экспериментов, которые бы могли позволить опытным путем определить наиболее оптимальные параметры сварки. Высокие издержки вызваны необходимостью проведения этапов наладки и отработки, исследования предыдущих результатов сварки с однотипными условиями, а также стоимостью ресурсов: оборудование, специалисты и исходные материалы для соединения.

Решение озвученной ранее проблемы позволит снизить издержки производства и сократить время, потраченное на каждый этап проведения ЭЛС. Все вышесказанное подтверждает необходимость поиска методов эффективной реализации настройки и преобразования параметров технологического процесса.

ПОСТАНОВКА ЗАДАЧИ

Необходимо проанализировать существующие методы машинного обучения, позволяющие решить задачу регрессии, в которой требуется найти математическую зависимость между набором исходных параметров процесса ЭЛС и результатом процесса при этих параметрах.

В качестве исходных данных выступают результаты экспериментов, проводимых в целях улучшения технологического процесса ЭЛС изделия, сборка которого состоит из двух частей разнородного материала. Эксперименты проводились специалистами АО «Информационные спутниковые системы» имени академика М. Ф. Решетнёва». В процессе выполнения работ были проведены 72 эксперимента.

Установка ЭЛС, на которой проводились исследования, предназначена для сварки электронным лучом в глубоком вакууме ДСЕ из нержавеющих сталей, титановых, алюминиевых и специальных сплавов. Имеющаяся установка ЭЛС обеспечивает повторяемость режимов в рамках возможностей имеющейся системы управления.

Математическая постановка задачи в данном случае будет выглядеть следующим образом. Пусть имеются набор параметров технологического процесса: IW – величина сварочного тока; IF – ток фокусировки электронного луча; VW – скорость перемещения луча по поверхности изделия; FP – расстояние от электронно-оптической системы до поверхности детали и результаты технологического процесса: depth – глубина сварного шва; width – ширина сварного шва.

В рамках данной работы имеем:

• 1.    Набор данных D 1 :

• 2.    Модель F(x_iw,x_i f ,x_vw,X f _p), которая предсказывает значения для каждого объекта Y(y_d epth , y width )-

• 3.    Оценка G(х i _w, х ф х_vw, х ^р , Y, F) - оценка точности прогнозирования модели.

D1 = {х iwi,x if^,■хvwi,хfр^,yd ер th^y wid th f) i=i> где n - количество экспериментов; х^ - ток сварки, мА; х^ - ток фокусировки, мА; хvw - скорость сварки, об/мин; х^р - расстояние до ЭОС, мм; y

Итак, необходимо найти такую модель F, которая обладает наилучшей мерой качества G.

МАТЕРИАЛЫ И МЕТОДЫ

Для моделирования предлагается исследовать следующие эффективные и широко применяемые на практике при решении задач регрессии методы машинного обучения:

• 1.    линейная регрессия (гребневая регрессия);

• 2.    искусственная нейронная сеть (ИНС);

• 3.    ансамбль «Случайный лес»;

• 4.    градиентный бустинг.

Также необходимо рассмотреть использование автоматизированной настройки гиперпараметров в разрезе каждой модели прогнозирования для получения оптимальных гиперпараметров.

Для оценки регрессионной модели чаще всего используют значения средней квадратической ошибки MSE, средней абсолютной ошибки MAE и коэффициента детерминации R². Средняя квадратическая ошибка вычисляется следующим образом:

п-1

MSE(у,y) =  У (yi - yi)2,

п Z—i i=0

где y - прогнозируемое i-ое значение, у - истинное i-ое значение, ап- количество наблюдений в выборке.

Средняя абсолютная ошибка определяется уравнением:

п-1

МЛЕ(у,у)= У^-^Ь п i=0

Оценка MAE менее чувствительна к выбросам, как средняя квадратическая ошибка.

Коэффициент детерминации отражает объясняющую способность регрессии f (X ^ Y) и определяется, как доля дисперсии зависимой переменной, объяснённая регрессионной моделью с данным набором независимых переменных. Обычно определяется как единица минус доля необъяснённой дисперсии, т.е.:

R2 = 1 -

^И(У1 - yi)2

£i(yi-yd2'

где

• •    SSE = Zi(yi - yi)²- сумма квадратов остатков регрессии;

• •    SST = ^i(yi - y^i)²-полная сумма квадратов, т.е. сумма квадратов отклонений точек данных от среднего значения регрессии;

• •    Х^п= (x_i; y_i)n=1- набор данных из n наблюдений;

• •    yi Е Yy = ^121;

• •    yi = №У

На практике, если коэффициент детерминации близок к 1, это указывает на то, что модель работает очень хорошо (имеет высокую значимость), а если к 0, то это означает низкую значимость модели, когда входная переменная плохо «объясняет» поведение выходной, т.е. линейная зависимость между ними отсутствует. Очевидно, что такая модель будет иметь низкую эффективность.

Линейная регрессия (гребневая регрессия)

Построение простой линейной модели с коэффициентами w = (w1,..., w_p) в scikit-learn происходит через минимизацию остаточной суммы квадратов между X и y:

min||XW -y||2 w               '2

В пакете scikit-learn [9] реализованы линейные модели с L2 и L1 регуляризацией – Ridge, Lasso.

Ridge решает проблемы обычных наименьших квадратов путем наложения штрафа на размер коэффициентов. Коэффициенты гребня минимизируют штрафную остаточную сумму квадратов:

min||XW —y||2 + a||W||2

Параметр сложности a>0 контролирует величину усадки: чем больше значение, тем больше величина усадки и, следовательно, коэффициенты становятся более устойчивыми к коллинеарности.

Lasso представляет собой линейную модель, которая оценивает разреженные коэффициенты. Это полезно в некоторых контекстах из-за его тенденции отдавать предпочтение решениям с меньшим количеством ненулевых коэффициентов, эффективно уменьшая количество параметров, от которых зависит данное решение.

Перед созданием полиноминальной регрессии необходимо воспользоваться предварительной обработкой данных из scikit-learn – Polynomial Features [9]. Она создает новую матрицу объектов, состоящую из всех полиномиальных комбинаций объектов со степенью (degree), меньшей или равной указанной степени. Расширяя пространство гипотез до всех полиномов степени p (degree = p), линейная модель будет иметь вид: f(X) = W0 + W1X1 + W₂X₂ +----+ W_pX_p + W₁₂X2 + W₂₂X1X₂ +----+ W_p2X1X_p +----+ WppXp

+ —

Если degree = 2, линейная модель для четырех параметров примет вид:

/(X) = W0 + W1X1 + W2X2 + W3X3 + W4X4 + W11X2 + W12X1X2 + W13X1X3 + W14X1X4 + — + W41X4X1 + W42X4X2 + W43X4X3 + W44X2

Обязательным этапом подготовки данных является их стандартизация, которую можно осуществить через функцию Standard Scaler пакета sklearn.preprocessing [9]. Стандартизация набора данных является общим требованием для многих оценщиков машинного обучения: они могут показывать плохие результаты, если отдельные параметры не выглядят более или менее похожими на стандартные нормально распределенные данные.

Информатика. Экономика. Управление// Informatics, Economics, Management 2023; 2(1)

Стандартизация набора данных в Standard Scaler происходит путем удаления среднего значения и масштабирования до дисперсии единиц.

Стандартная оценка для каждой переменной h из обучающей выборки рассчитывается как:

z = (h-u) s где u - среднее значение обучающих выборок; s - стандартное отклонение обучающих выборок.

Существуют следующие гиперпараметры для настройки модели:

• •    degree — степень полинома;

• •    alpha — cила регуляризации.

Для оценки регрессионной модели чаще всего используют значения среднеквадратической ошибки MSE и коэффициента детерминации R².

Искусственная нейронная сеть (ИНС)

Под нейронными сетями подразумеваются адаптируемые обучаемые распараллеленные вычислительные структуры, состоящие из большого числа математических единиц, способных динамически изменять свои значения -искусственных нейронов [10]. В состав нейрона входят синапсы, сумматоры и нелинейный преобразователь. Синапсы осуществляют связь между нейронами и характеризуют силу сигнала между этими нейронами (либо усиливаясь, либо слабея). Сумматор выполняют сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента — выхода сумматора. Эта функция называется функцией активации или передаточной функцией нейрона. Математическая модель нейрона описывается соотношением:

У = fd^iWiXt + b), где Wt - вес синапса; b — значение смещения; Xt - компонент входного вектора (входной сигнал); у - выходной сигнал нейрона, п - число входов нейрона; f - нелинейное преобразование (функция активации или передаточная функция).

Ключевыми задачами при построении нейронных сетей является определение:

• •    архитектуры сети;

• •    оптимизаторов;

• •    функций потерь;

• •    функций активации.

Для решения задачи регрессии наиболее подходящей архитектурой сети является многослойная нейронная сеть, функцией потери – среднеквадратическая ошибка. Другие параметры чаще всего определяются через опыт предыдущих исследований или через проведение определенного количества экспериментов. К таким параметрам относятся:

• •    начальные значения весов;

• •    оптимизатор;

• •    функция активации;

• •    количество нейронов в скрытом слое;

• •    количество эпох обучения;

• •    размер партии входных данных для одной эпохи обучения;

• •    скорость обучения для оптимизатора.

Оценка качества работы ИНС осуществляется с помощью значения функции потерь на последнем шаге итерации обучения (абсолютная ошибка) или с помощью MSE. Также важно отследить момент возникновения переобучения сети: это можно сделать с помощью использования валидационной выборки, которая берется из обучающей на каждой эпохе. Вычисляется критерий качества работы сети для обоих множеств: обучающего и проверочного. Если с какой-то итерации графики начинают расходиться, то делается вывод, что ИНС переобучается и процесс обучения следует прервать. Избежать переобучения помогут регуляризации L1 и L2, а также метод Dropout.

Для построения нейронных сетей будет использоваться Keras [12], оболочка над Tensorflow [13]. При необходимости более гибкой настройки ИНС всегда можно вернуться к использованию TensorFlow.

Ансамбль случайных лесов

Реализацией модели ансамбля случайных лесов в пакете scikit-learn [9] является Random Forest Regressor (RFR). RFR включает в себя метод Extra-Trees - алгоритм усреднения для повышения точности прогнозирования и контроля чрезмерной подгонки, основанный на рандомизированных деревьях решений.

В RFR каждое дерево в ансамбле строится из выборки, взятой с заменой (метод bootstrap) из обучающего набора. Кроме того, при разделении каждого узла во время построения дерева наилучшее разделение определяется по всем входным параметрам.

Алгоритм построения случайного леса, состоящего из N (параметр n_estimators)

деревьев, выглядит следующим образом: для каждого п = 1,..., N:

• 1)    генерируется выборка Х_л с помощью bootstrap;

• 2)    происходит построение решающего дерева Ь_л по выборке Х_л:

• a)    по заданному критерию (параметр criterion) выбирается лучший признак, делается разбиение в дереве по нему и так до исчерпания выборки;

• b)    дерево строится, пока в каждом листе не более п^ объектов (параметр min_samples_leaf) или пока не достигнем определенной глубины дерева (параметр max_depth);

• c)    при каждом разбиении сначала выбирается m случайных признаков (параметр max_features) из n исходных, и оптимальное разделение выборки ищется только среди них.

Итоговое решение является средним значением:

N

1,1 N у» :-:

i=i

Основные гиперпараметры в RFR, которые подбираются для поиска оптимального решения:

• •    n_estimators — число деревьев в "лесу";

• •    criterion — функция, которая измеряет качество разбиения ветки дерева (MSE, MAE);

• •    max_depth — максимальная глубина дерева;

• •    max_features — число признаков, по которым ищется разбиение;

• •    min_samples_leaf — минимальное число объектов в листе;

• •    min_samples_split — минимальное количество объектов, необходимое для разделения внутреннего узла дерева.

Также, при построении случайных лесов, можно решить дополнительную полезную задачу: определить наиболее важные переменные для разбиения – чем чаще переменная встречается в разбиении лесов, тем сильнее она оказывает влияние на образование результирующих переменных.

Оценка качества работы ансамбля случайного леса осуществляется с помощью меры точности и ROC-анализа.

Градиентный бустинг

Градиентный бустинг будет осуществляться над деревьями решений. Главная идея бустинга заключается в том, ансамбль деревьев решений строится не параллельно (при бэггинге), а последовательно. Простыми словами, каждое последующее построенное дерево учится на ошибках предыдущего. В scikit-learn [9] модель Gradient Boosting Regressor (GBR) строит аддитивную модель поэтапно; это позволяет оптимизировать произвольные дифференцируемые функции потерь. На каждом этапе дерево решений соответствует отрицательному градиенту заданной функции потерь.

Алгоритм GBR [11]:

1) инициализируется модель константным значением /(x) = /₀, /₀ = у,уе R"-

п

Ъ = argmin ^L(yi, у) ;

Y 1=1

• 2)    для каждой итерации t = 1, ^,М (M - параметр n_estimators) повторяется:

  а)

  
  

подсчет псевдо-остатков r_t:

ГdL(yi^x))l

lt       |    9/(xt)    J            ......

J ^(Л)=)^(Л)

b)

c)

d)

e)

построение нового базового алгоритма h_t(x') как регрессию на псевдоостатках ^{(х_ьг_иУ}1=1,.,_п;

нахождение оптимального коэффициента p_t при ^_t(x) относительно исходной функции потерь (параметр loss):

п

Pt = argmin } L(yt,/(xt) + p • h(xt, 9)) ; p    t=i

сохранение /t(x) = pt • tht(x);

обновление текущего приближения /(x):

/?(x)^ f(x)+/t(x)= ]T/i(x);

1=0

• 3)    екомпоновка итоговой модели /(x):

/(x)= )T/,(x).

1=0

Основные гиперпараметры в  GBR, которые подбираются для поиска оптимального решения:

• •    n_estimators — количество этапов повышения градиента (количество

используемых слабых деревьев решений);

• •    loss — функция потерь для оптимизации. (MSE, MAE);

• •    max_depth — максимальная глубина каждого дерева решений;

• •    max_features — число признаков, по которым ищется разбиение;

• •    min_samples_split — минимальное количество объектов, необходимое для разделения внутреннего узла дерева;

• •    min_samples_leaf — минимальное число объектов в листе.

Настройка гиперпараметров

Главная идея настройки гиперпараметров состоит в том, чтобы найти наиболее оптимальную комбинацию гиперпараметров, который позволяет получать модели с более высокими оценками качества.

Существует несколько методов оптимизации гиперпараметров:

• 1)    ручной поиск;

• 2)    случайный поиск;

• 3)    поиск по сетке;

• 4)    автоматическая настройка (Байесовская оптимизация, генетические алгоритмы);

• 5)    настройка искусственных нейронных сетей (ANNs).

В ручном поиске предполагается подбор гиперпараметров на основе прошлого опыта специалиста и экспериментов. После каждого подбора осуществляется пересмотр точности результатов модели и, при недостижении необходимой точности, заново осуществляется подбор новых гиперпараметров.

Случайный поиск предполагается использование методов комбинаторики и предполагает создание сетки всех возможных сочетаний значений гиперпараметров. В случайном поиске часто используют перекрестную проверку, которая позволяет избежать использования некоторых гиперпараметров, плохо работающими либо на тренировочных данных, либо на тестовых. Для реализации случайного поиска гиперпараметров     используется     метод     RandomizedSearchCV     пакета sklearn.model_selection [9].

В поиске по сетке используется сетка гиперпараметров, на которой обучают и тестируют модель на каждой из возможных комбинаций. Хорошей практикой является использование поиска по сетке с использованием гиперпараметров, показавшие высокое качество модели после случайного поиска. Для реализации случайного поиска гиперпараметров используется метод GridSearchCV пакета sklearn.model_selection [9].

Автоматическая настройка гиперпараметров используют идеи байесовской оптимизации, градиентного спуска, а также эволюционные алгоритмы.

Для настройки гиперпараметров нейронных сетей используются аналогические методы, что и для других моделей. Для этого используется класс KerasClassifier пакета scikeras.wrappers [14].

Концепция системы поддержки и принятия решений. Изначальный прототип системы предположительно будет состоять из 4 компонентов:

• •    модуль ввода параметров технологического процесса осуществляет ввод и редактирование параметров процесса ЭЛС;

• •    модуль аналитики, осуществляющий прогноз на основе введенных параметров технологического процесса;

• •    модуль вывода информации о прогнозе параметров сварочного шва осуществляет построение графиков, визуализирующих результаты прогноза;

• •    модуль обработки данных прошлых технологических процессов позволяющий добавлять/редактировать/удалять результаты прогнозирования на основе параметров прошлых технологических решений.

В рамках работы с системой возможно появление следующих основных сценариев:

• •    использование новых параметров технологического процесса ЭЛС, осуществления прогнозирования параметров шва, сохранение в БД;

• •    использование прошлых параметров технологического процесса.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Использование определенной модели машинного обучения зависит от целей и задач исследования. Каждая модель характеризуется своей производительностью, сложностью создания, интерпретируемостью, настраиваемостью и прочими факторами, которыми играют важную роль на этапе реализации.

Важно понимать, что нельзя ограничивать исследование только одним типом модели: каждая модель позволяет получить новое знание об исходных данных, зависимостях между входными и выходными значениями, наиболее оптимальную комбинацию гиперпараметров модели. Существует огромное множество методов, которые позволяют оптимизировать результаты моделей машинного обучения и игнорирование их является нецелесообразным.

ЗАКЛЮЧЕНИЕ

В рамках исследования были собраны данные о моделях машинного обучения, способных решить задачу регрессии: алгоритмы решения, оценки качества, оптимизационные алгоритмы и пакеты для реализации моделей.

В перспективе планируется провести реализацию каждой их этих моделей с использованием автоматизированной настройки гиперпараметров, провести сравнительный анализ моделей, систематизировать результаты анализа с помощью инструментов визуализации, оценить наиболее важные переменные, влияющие на результирующие значения, и, в итоге, выбрать наилучшую из построенных моделей.