Применение методов машинного обучения при проектировании камер сгорания газотурбинных двигателей

Задачи проектирования элементов, узлов и конструкций авиационных двигателей решаются с использованием методов вычислительной газодинамики, специализированных программных комплексов (Ansys Fluent1, STAR-CCM+2, OpenFOAM3, FLOW-3D4 и др.) и больших вычислительных ресурсов [1]. К такой задаче можно отнести проектирование элементов камер сгорания (КС) газотурбинных двигателей (ГТД). Важным требованием к КС ГТД является обеспечение потерь полного давления (ППД), не превышающих значений, установленных техническим заданием на проектирование КС [2, 3]. Примерно две трети ППД в КС обусловлены процессами горения и смешения. Остальные потери приходятся на диффузор, который обеспечивает торможение потока воздуха, выходящего из компрессора и его распределение по кольцевым каналам КС. Снижение ППД в диффузоре улучшает характеристики КС и повышает эффективность двигателя в целом [2-5].

Первичный облик КС определяется выбранным прототипом. Проектировочный расчёт прототипа КС позволяет установить: габариты диффузора, геометрию фронтового устройства, объём и габариты жаровой трубы, длину газосборника и т.д.Упрощённая геометрическая модель КС используется для трёхмерного моделирования процессов средствами вычислительной гидродинамики ( Computational Fluid Dynamics, CFD ) [1]. В результате итеративного процесса CFD -расчётов получается окончательный вариант проекта конструкции.

Целью данной работы является попытка применения методов интеллектуального анализа данных (ИАД) [6-10] к проектированию проточной части диффузора КС ГТД. В практике проектирования КС используется специализированное программное средство «Optimization » в Ansys 1 , с помощью которого определяют геометрию диффузора, обеспечивающую минимальные ППД и его распределение по каналам КС. Время поиска решения может составлять от нескольких дней до нескольких недель. В результате создаётся большой объём данных, который можно использовать для обучения нейронной сети (НС). Предиктивная аналитика, базирующаяся на использовании нейросетевых моделей, способна быстро и точно прогнозировать различные результаты и явления. Количество и структура данных, по которым проходит обучение моделей, оказывает существенное влияние на их прогностическую способность. Например, недостаточное количество данных влияет на качество и точность прогноза, а увеличение количества данных позволит повысить точность, но может привести к переобучению [11].

• 1    Выбор методов машинного обучения

Предиктивная аналитика объединят методы ИАД и прогнозного моделирования с целью прогнозирования будущих событий [6]. Она представляет собой набор инструментов, включающий методы анализа больших данных и статистические методы. Использование различных алгоритмов ИАД позволяет обнаруживать скрытые закономерности, выявлять неизвестные зависимости и обучаться [7].

На начальных этапах ИАД выполняют подготовку и преобразование данных [7, 12]. Частью преобразования является очистка данных, в процессе которой устраняются дубликаты, многозначность, аномалии, пропущенные значения и т.п. Одним из распространённых алгоритмов преобразования является нормализация [13]. Другим важным алгоритмом преобразования является обобщение, позволяющее объединить данные в категории для более глубокого понимания зависимостей [14].

Перед обучением нейросетевой модели данные необходимо разделить на выборки [13]. Обычно используются два типа выборок: контрольная и тренировочная. На контрольную выборку отводится 20%, на тренировочную 80%. Тренировочная выборка разделяется ещё на две: 70% - обучающая и 30% - тестовая выборки. Обучающая выборка используется для обучения модели, тестовая - для оценки её качества, а контрольная - для выбора наилучшей модели.

Следующим этапом определяется тип задачи, решаемой ИАД. Среди основных задач: регрессия, классификация и кластеризация [15]. После этого данные могут обрабатываться посредством построения моделей, онтологических конструкций и других методов. В данной работе применены рекуррентная НС (РНС) с долгой краткосрочной памятью ( Long Short-Term Memory, LSTM), способная обучаться долгосрочным зависимостям [16], и алгоритм машинного обучения с применением градиентного бустинга над деревьями решений ( Categorical Boosting, CatBoost ) [17].

РНС с долгой краткосрочной памятью способна хранить информацию на протяжении продолжительного времени. На рисунке 1 представлена схема искусственной НС, которая состоит из трёх типов слоёв [18]: ■    входной - получает данные;

• ■    скрытый - обрабатывает информацию и может состоять из нескольких скрытых слоёв, количество кото

рых зависит от сложности задачи;

• ■    выходной - генерирует результат.

Каждый нейрон, называемый также сумматором, получает входные сигналы с весами, отражающими их значимость [19]. Нейрон суммирует входные сигналы, умножая их на соответствующие веса. РНС представляют собой последовательность одинаковых сетей, позволяющих запоминать и передавать информацию [20]. Схема работы РНС приведена на рисунке 2.

РНС демонстрируют высокую эффективность при решении задач многомерного прогнозирования и моделирования нелинейных взаимосвязей и не требуют большого количества данных, как глубокие НС [21].

РНС имеют ограниченную способность запоминать информацию на протяжении длительных периодов. Поэтому применяется архитектура LSTM , которая позволяет НС хранить и обрабатывать информацию в

Входной слой Скрытые слои

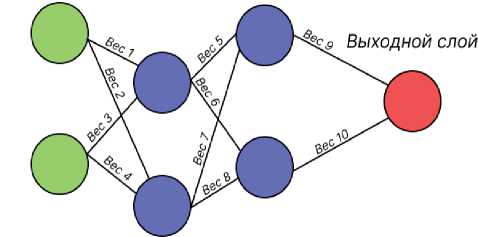
Рисунок 1 - Схема модели искусственной нейронной сети

течение длительного времени. LSTM -сети сохраняют состояние ячейки, содержащее информацию, необходимую для запоминания. Управление доступом к информации, хранящейся в состоянии ячейки, осуществляется посредством фильтров, включающих сигмоидальный слой [21]. Схематическое представление архитектуры LSTM приведено на рисунке 3.

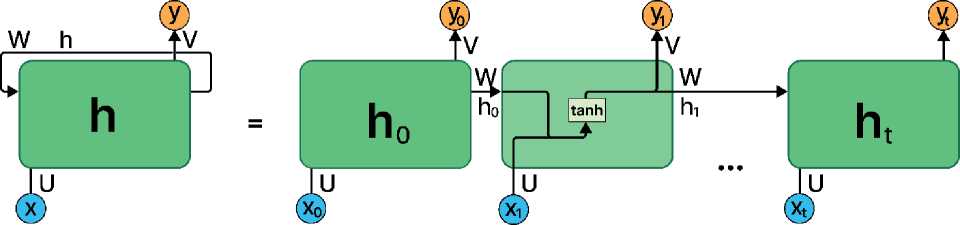
U — матрица весов для входных данных; V — матрица весов для выходных данных; W — матрица весов

для рекуррентных входных данных; xt — входное значение в момент времени t ; y_t — выходное значение в момент времени t ; h_t — вектор результата активации скрытых нейронов в момент времени t

Рисунок 2 - Схема рекуррентной нейронной сети

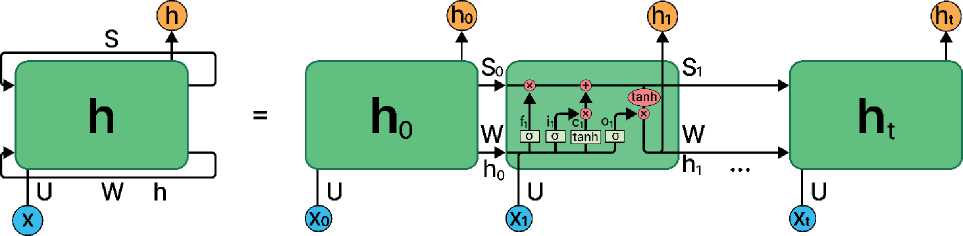
Рисунок 3 - Схема нейронной сети с долгой краткосрочной памятью

В условиях ограниченного объёма обучающей выборки целесообразно использовать алгоритмы машинного обучения с применением градиентного бустинга. Градиентный бустинг отличается устойчивостью при недостаточном объёме данных и эффективностью работы с табличными данными. В качестве входных данных принимаются множества X, Y и используется пространство вещественных чисел в качестве оценок. Описать принцип градиентного бустинга можно следующей формулой [22]: a ( x ) = C ( b ( x )), где b : X ^ R - алгоритмический оператор (базовый алгоритм), а функция C : R ^ Y называется решающим правилом.

Схема алгоритм градиентного бустинга представлена на рисунке 4. В отличие от НС алгоритм градиентного бустинга может обрабатывать данные разных типов. Он применим для прогнозирования числовых значений (регрессия) и для классификации объектов. CatBoost эффективно обрабатывает нелинейные зависимости в дан- ных, а применение L 2-регуляризации, осуществляющей штрафование больших весов модели, способствует улучшению обобщающей способности алгоритма [23]:

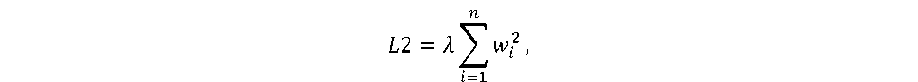
где Л - коэффициент регуляризации, n - количество элементов в векторе весов, w i - i -тый элемент вектора весов.

Оценка качества построенной модели осуществляется посредством анализа метрик, релевантных решаемой задаче. Для задач классификации применяется метрика точности, а для задач регрессии -среднеквадратичная ошибка ( Mean Squared Error , MSE ). Другим методом оценки является кроссвалидация, в частности, метод k-Fold [13], который включает разделение исходного набора данных на к непересекающихся частей (фолдов). В ходе к итера-

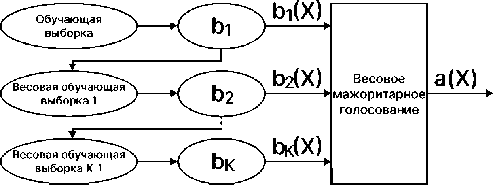
Рисунок 4 - Схема алгоритма градиентного бустинга

ций каждый из k фолдов поочерёдно используется в качестве тестовой выборки, а оставшиеся к- 1 фолды - в качестве обучающей выборки. По завершении к итераций формируется к оценок качества, усреднённое значение которых характеризует общую эффективность модели.

• 2    Задача проектирования диффузора камеры сгорания ГТД

Уровень ППД современных КС лежит в диапазоне 4,5-6,5% и определяется по формуле:

Др* =       100%,                             (1)

где Р*_х - полное давление на входе в диффузор; Р_в*_ых - полное давление на выходе из КС.

Около 3-3,5% ППД возникают в процессах смесеобразования, горения и смешения в жаровой трубе КС, 1-3% - при торможении потока воздуха, выходящего из компрессора, и его распределении по кольцевым каналам КС [2, 3].

Объектом исследования является диффузор КС с внезапным расширением, схема которого представлена на рисунке 5. Для трёхмерного CFD -расчёта рассмотрен сектор диффузора (10°) кольцевой КС. В процессе расчёта положения входного и выходного сечений и их размеры оставались неизменными. Элементы внутреннего и внешнего корпусов приняты линейными для упрощения автоматического построения конечно-элементной модели (КЭМ). Геометрия диффузора определена следующими параметрами: L^- длина диффузора, d^ -диаметр до точки пересечения линии угла нацеливания а с выходным сечением диффузора, а 1 и а ₂ -углы раскрытия стенок диффузора.

Линейные и угловые размеры варьировались в

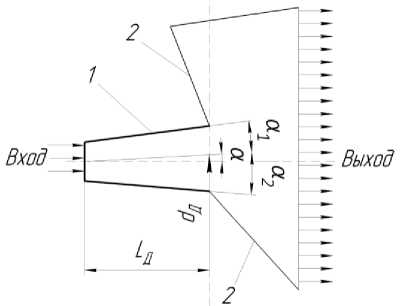
1 - диффузор, 2 - элементы корпуса

Рисунок 5 - Схема конструкции диффузора КС с внезапным расширением

диапазонах, основанных на экспериментальных данных, включённых в методики одномерного проектирования [3, 24, 25]: угол раскрытия диффузора 9°...11°; Ьд = 63^77 мм; dд = 456^558 мм.

Для CFD -расчёта создана КЭМ с максимальным размером элемента 1,2 мм и минимальным 0,15 мм. Количество элементов в модели во всех вариантах расчёта составило около 200 тыс. элементов. Ортогональное качество элементов модели 0,2.

Расчёты выполнялись для значений давления на входе в КС в диапазоне 3,2- 5,2 МПа, что соответствовало режимам работы ГТД во время взлёта и посадки.

Выполнены расчёты 2142 вариантов геометрии диффузора. На каждом шаге автоматического расчёта записывались значения всех геометрических параметров диффузора, давления на выходе и рассчитывались ППД. Минимальное значение ППД принято за эталон. На полученных значениях обучены нейросетевая модель и алгоритм градиентного бустинга. Результаты прогнозов верифицированы по CFD -расчёту.

Для сравнения потерь, предсказанных методами РНС и CatBoost , и потерь, полученных в результате CFD -расчёта, определена относительная погрешность

£ _ |Др predicted-^ CFd\ ^ q q 0 /                                    Г 2 'j где Pp*peed-ted - предсказанные ППД; CFD-fd - ППД, полученный в результате CFD-расчёта.

• 3    Реализация методов LSTM и CatBoost

  Для реализации методов LSTM и CatBoost на Python использовались данные, полученные при трёхмерном численном моделировании диффузора. Набор данных содержит восемь столбцов значений: входное и выходное давления, процент потерь и пять геометрических параметров диффузора. После предварительной обработки данных (2142 варианта), включающей удаление дубликатов и строк с пропущенными значениями, он был сокращён до 1720. Нормализация данных выполнена тремя методами: минимума-максимума; Z-масштабирования; на основе среднего значения [26]. Данные были разделены на обучающую, тестовую и контрольную выборки и преобразованы в формат, совместимый с используемыми методами машинного обучения.

Для построения и оценки моделей LSTM использовался фреймворк Keeas [27]. Архитектура модели включала входной слой, заданное количество скрытых слоёв и выходной слой, оптимизированный с помощью алгоритма Adam [28]. Перебор гиперпараметров, включая точность обучения, размер пакета данных, тип нормализации и количество скрытых слоёв, проводился с использованием кросс-валидации и отрицательной среднеквадратичной ошибки в качестве функции потерь. Обучение модели осуществлялось с использованием лучших параметров, определённых в процессе перебора, и последующим восстановлением исходных значений для оценки результатов.

Для оценки влияния предобработки данных на эффективность алгоритма градиентного бустинга деревья решений были протестированы на данных с различными типами нормализации, а также на исходном, ненормализованном наборе данных. С целью оптимизации гиперпараметров каждой модели CatBoost (обученной на данных с различными типами нормализации) был реализован поиск по сетке с варьированием скорости обучения, глубины дерева, количества итераций и коэффициента L 2-регуляризации. Оценка качества моделей производилась посредством кросс-валидации с использованием MultiRMSE [17]:

MultiRMSE - ^^Т^У^^аУ, где N — количество наблюдений в выборке; dim - количество зависимых переменных; yld — истинное значение d-го признака для i-го наблюдения; yid — предсказанное моделью значение d-го признака для i-го наблюдения.

Перед проведением вычислительного эксперимента выполняется настройка моделей. Из набора данных выделена тестовая выборка, на которой методом geid seaech [29] определены гиперпараметры моделей: тип нормализации данных; количество скрытых слоёв; размеры пакетов данных; количество итераций; коэффициенты регуляризации; глубина и точность обучения. Гиперпараметры для методов LSTM и CatBoost представлены в таблице 1. Тип нормализация для метода LSTM был выбран максимально-минимальный, точность обучения составила 0,001, а для метода CatBoost – 0,1. Схемы моделей, применённые для каждого метода, представлены на рисунках 6-8.

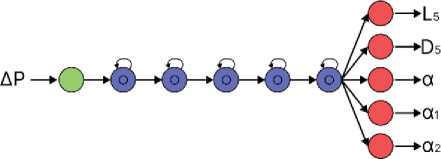
Рисунок 6 – Схема модели, предиктором которой является потеря полного давления в диффузоре

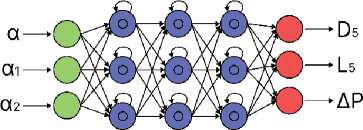
Рисунок 7 – Схема модели, предикторами которой являются углы раскрытия диффузора и наклона осевой линии

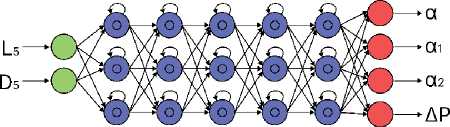
Рисунок 8 – Схема модели, предикторами которой являются линейные параметры диффузора

Таблица 1 – Гиперпараметры методов LSTM и CatBoost

Метод	LSTM		CatBoost
Гиперпараметры	Количество скрытых слоев	Размер пакета данных	Количество итераций	Коэффициент регуляризации	Глубина
По проценту потерь	5	1	1000	5	4
По углам	3	1	3000	7	10
По линейным параметрам	5	15	3000	7	15

• 4    Вычислительный эксперимент и анализ результатов

0.0         0.2         0.4         0.6         0.8         1.0

В ходе вычислительного эксперимента верифицировались значения ППД, предсказанные методами LSTM и CatBoost со значениями ППД, полученными в результате численного моделирования диффузора в Ansys Fluent . Модель диффузора строилась по спрогнозированным геометрическим параметрам. Значения входных параметров для каждой модели задавались случайным образом из принятых диапазонов (см. раздел 2). В модели, предиктором которой был процент ППД, задаваемый диапазон ограничен максимальным значением 1,1%.

В таблице 2 представлены примеры трёх строк из набора данных, полученного в результате расчётов в Ansys Fluent . Входные параметры для моделей LSTM и CatBoost брались из этих строк, выходные – предсказывались. По ним строилась геометрия диффузора и проводился верификационный расчёт прогноза по моделям LSTM и CatBoost .

Вычислительный эксперимент повторен 12 раз. Определены погрешности спрогнозированных процентов ППД от эталонных, полученных в результате расчётов в Ansys Fluent . Построены графики зависимости погрешности от спрогнозированного процента потерь (рисунки 9 и 10). Для каждой модели определено среднее значение погрешности предсказанных ППД. Метод CatBoost обеспечивает наилучшую точность предсказания геометрических параметров диффузора по проценту потерь (средняя погрешность 1,64%). Сводные данные приведены в таблице 3.

Таблица 2 – Полученные параметры диффузора с помощью разных алгоритмов на трёх наборах предикторов

Методы	Набор X	, мм	, мм	α, град	α 1 , град	α 2 , град	, МПа	, МПа	, %
Ansys	По проценту потерь	72,69	466,26	2,39	5,80	6,10	5,230	5,249	0,36
	По углам	77,70	522,00	2,50	4,57	5,77	3,179	3,205	0,80
	По линейным параметрам	75,00	542,00	1,50	3,60	5,40	3,183	3,205	0,66
CatBoost	По проценту потерь	73,20	468,80	2,30	6,10	6,20	5,230	5,249	0,36
	По углам	77,20	538,40	2,50	4,57	5,77	3,176	3,205	0,90
	По линейным параметрам	75,00	542,00	1,90	4,50	5,80	3,186	3,205	0,56
Верификация прогноза CatBoost	По проценту потерь	73,20	468,80	2,30	6,10	6,20	5,227	5,249	0,37
	По углам	77,20	538,40	2,50	4,57	5,77	3,175	3,205	0,93
	По линейным параметрам	75,00	542,00	1,90	4,50	5,80	3,186	3,205	0,58
LSTM	По проценту потерь	79,00	453,60	2,74	6,64	6,90	3,190	3,202	0,36
	По углам	79,67	491,08	2,50	4,57	5,77	4,587	4,641	1,17
	По линейным параметрам	75,00	542,00	2,50	4,57	5,77	4,458	4,508	1,12
Верификация прогноза LSTM	По проценту потерь	79,00	453,60	2,74	6,64	6,90	3,190	3,202	0,38
	По углам	79,67	491,08	2,50	4,57	5,77	4,580	4,641	1,30
	По линейным параметрам	75,00	542,00	2,50	4,57	5,77	4,450	4,509	1,29

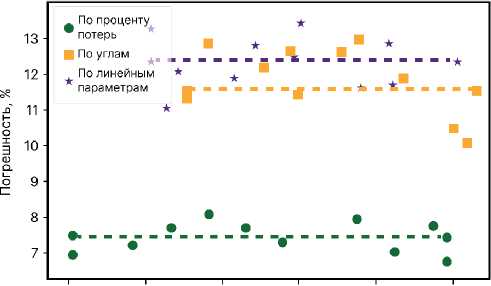
• По проценту потерь

■ По углам

★ По линейным параметрам

0.0         0.2         0.4         0.6         0.8         1.0

Процент потерь модели

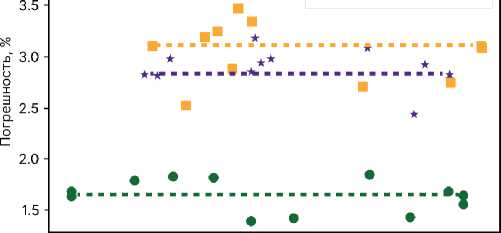
Рисунок 9 – Зависимости погрешности моделей

CatBoost , среднее значение погрешности модели (пунктирная линия)

Процент потерь модели

Рисунок 10 – Зависимости погрешности моделей LSTM , среднее значение погрешности модели (пунктирная линия)

Таблица 3 – Средние значения погрешностей методов

Методы	Модели
	По потерям, X =	По углам, X= {α, α1, α2}	По линейным параметрам X= {  ,  }
CatBoost	1,64%	3,11%	2,84%
LSTM	7,28%	11,39%	12,19%

Для взаимодействия с обученными моделями создан веб-интерфейс с использованием следующих технологий.

• ■   React 5 : библиотека JavaScript , обеспечивающая динамическое обновление пользовательского интерфейса.

• ■    Material UI (MUI)⁶: библиотека готовых компонентов пользовательского интерфейса.

• ■   React-hot-toast ⁷: инструмент для визуализации .

• ■   Flask 8 : фреймворк для разработки серверной часть системы.

Заключение

В работе проведено сравнение вариантов применения методов, использующих нейросетевую LSTM модель и алгоритм градиентного бустинга CatBoost , для проектирования диффузора КС ГТД. Анализ полученных результатов показал, что CatBoost предпочтителен при имеющемся объёме обучающих данных. Средняя погрешность CatBoost составила 1,64%.

Формирование базы данных, полученных с помощью CFD -расчётов, позволило на основе машинного обучения существенно сократить время предварительной оценки геометрических параметров диффузора КС ГТД.