Применение модели память-предсказание к решению задачи распознавания образов
Автор: Болотова Юлия Александровна, Спицын Владимир Григорьевич
Журнал: Проблемы информатики @problem-info
Рубрика: Средства и системы обработки и анализа данных
Статья в выпуске: S, 2011 года.
Бесплатный доступ
Предложена система распознавания образов с использованием модели память-предсказание, разработанной в Редвудском институте нейробиологии как новый подход к созданию искусственного интеллекта, основанный на структуре и принципах функционирования мозга млекопитающих. Модель имитирует работу органов чувств человека и может быть использована для решения задач распознавания образов, речи и прогнозирования.
Иерархическая временная память, распознавание образов, паттерны, нейросети
Короткий адрес: https://sciup.org/14320355
IDR: 14320355 | УДК: 004.931
Текст научной статьи Применение модели память-предсказание к решению задачи распознавания образов
В настоящее время при решении задачи распознавания образов используется активно развивающийся подход – нейронные сети, широкое распространение которого объясняется структурным сходством нейронных сетей с головным мозгом. Этот подход открыл новые возможности для создания искусственного интеллекта, однако достигнутые результаты все еще очень далеки от реальной работы человеческого мозга. Модель память-предсказаниеание, разработанная американскими учеными-нейрофизиологами [1], имеет не только структурное, но и функциональное сходство с работой головного мозга человека. По сути, модель является синтезом нейронных сетей, сетей Байеса и цепей Маркова.
В основе модели лежат два принципа, характерных для человеческого зрения в процессе обучения и восприятия изображений: учет временной составляющей в функции зрения и иерархичность процесса восприятия [2]. Целью настоящей работы являются анализ модели и реализация системы распознавания образов на ее основе.
Структура системы. Система организована в виде иерархической сети, включающей несколько уровней (рис. 1). Каждый уровень состоит из набора узлов. Узлы одного уровня не связаны между собой, каждый узел последующего уровня получает информацию с нескольких узлов предыдущего уровня, за счет чего область рецептивного поля узлов увеличивается с увеличением номера уровня.
Узлы могут находиться в двух состояниях: обучения и тестирования. Оба этапа начинаются с разбиения входного изображения на равные подобласти. В каждой подобласти формируется вектор признаков, который передается в определенный узел первого уровня. При работе с бинарными изображениями вектор представляет собой значения пикселей, при анализе полутоновых изображений - значения фильтров Габора. В узле проводится анализ вектора признаков, результаты которого передаются на следующий, более высокий уровень. На рис. 1 представлена сеть, включающая три уровня.
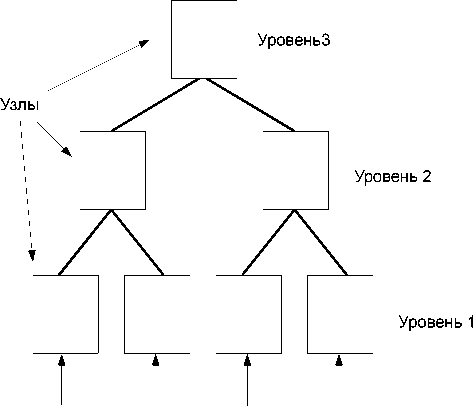
Вектор признаков
Структура узла. Основной особенностью Рис. 1. Структура модели модели является включение временной составляющей в процесс обучения и тестирования сети. Обязательным условием является представление входной информации (независимо от уровня иерархии) в виде последовательности равномерно смещающихся объектов. Модель была обу- чена на видеопоследовательностях, полученных горизонтальным, вертикальным и спиральным смещением объекта. Лучшие результаты получены при спиральном смещении [3].
На этапе обучения в узле сохраняются уникальные входные векторы X- (пространственные центры), содержащие информацию о пространственном расположении пикселей внутри рецептивного поля узла. Затем отслеживается частота следования пространственных центров друг за другом. Центры с наибольшей частотой следования объединяются во временные группы. Связь пространственного центра c i с временной группой g j сохраняется в матрице PCG [ i,j ] [4]. Таким образом, в каждом узле содержатся:
PCG g 1 g 2 gng
...
Матрица Временные группы
А y
-
- множество C пространственных центров c i , i = 1,..., П с ;
-
- множество G временных групп g j , j = 1,..., n g ;
Пространственные центры
c 1 c 2 c nc
...
f
1—-Р,Л-,..-, 1]
-
- матрица PCG размером nc х n g .
На этапе распознавания в узле выполняются две операции: анализ пространственного расположения элементов изображения и проверка инвариантности к смещению. Пространственный анализ осуществляется выбором пространственного центра, соответствующего входному вектору. Проверка инвариантности предполагает выбор временной группы, в которую входит выбранный пространственный центр ^ ^ ^
(рис. 2).
Рис. 2. Пример узла первого уровня
Пространственный анализ входных векторов. Пространственный анализ необходим для фильтрации и компрессии входных данных и их первичного обобщения. При обучении сети в узлах сохраняются уникальные входные векторы. Размерность пространственных центров зависит от номера уровня. Для узлов входного уровня размерность пространственных центров равна размерности входного вектора. При поступлении очередного вектора на вход происходит его сопоставление с уже сохраненными пространственными центрами (паттернами) по формуле
Pi = e-d2 a\ где di - евклидово расстояние между входным вектором и i-м паттерном; с - параметр, характеризующий степень вариации от центра квантизации (пропорционален степени зашумления выборки).
Для узлов остальных уровней каждый элемент паттерна c i [ j ] является индексом временной группы-победителя в дочернем узле child j ( N ). Таким образом, размерность паттернов равна количеству дочерних узлов данного узла. Например, если узел N принимает на вход вектор из четырех дочерних узлов, то его пространственный центр может иметь вид с 1 =[5, 3, 1, 1]. Здесь 5, 3, 1, 1 – номера групп-победителей в соответствующих дочерних узлах child 1 , child 2 , child 3 , child 4 [5].
Временной анализ входных векторов. Даже незначительное смещение объекта на изображении приводит к существенным изменениям пространственного расположения его пикселей. Временной анализ необходим для того, чтобы достичь инвариантности к смещению объектов. Временная группа представляет собой подмножество пространственных центров, которые часто следуют друг за другом и, следовательно, относятся к одному и тому же объекту (рис. 3).
Матрица PCG размерности n g × n c представляет собой матрицу соответствия пространственных центров временным группам. Элемент PCG [ i , j ] = P ( c i | g j ) определяет условную вероятность принадлежности с i группе g j . PCG нормируется по группам g j [6]:
nc
Е P ( c\ g j ) = 1.
i = 1
Метрика объединения центров в группы. Пусть g1,…,gn – набор временных групп, c1,...,cs – множество пространственных центров. Степень связанности центров внутри группы gi определяется по формуле tci=Л Е Е T (k, m) ni kegi megi где ni – число пространственных паттернов в группе gi; k – текущий паттерн в момент времени t – 1; m – текущий паттерн в момент времени t; T(k,m) – число следований паттернов k и m друг за другом.
Чем большее количество раз будет появляться та или иная последовательность внутри кластера, тем больше будет значение tс. Таким образом, имеем целевую функцию ng
J ( G ) = — Е tc ( g k ). ng k = 1
Необходимо создать набор временных групп {D i } i=1,...,n , при котором целевая функция принимает максимальное значение [3].
азшнтщввн аняиеисннк В9ШКЕ1ИВЗ юиппнапавЕ ЛБЕЕИВВаШЕ □шпЕппааяи Еаввввивнв тпшшшшивп □ишавваввв ЕЕЕЕЕЕЕЕПП ЕННПСНЛППВ □□зааэпэиз ллиллаив биНВЕЕЕИ g2: КЩ
63:ВВВВШ
-
64: ЭВ
-
65: ШИ
g6: НЭП б7:Шсваа
-
б8: ШЕИ
g9: ЛЕИ glO: BHG
611: ВШ
612:
Рис. 3. Узел первого уровня: а - пример пространственных паттернов; б - пример разбиения пространственных центров на временные группы g1 ^ g12
Режим тестирования. После того как все уровни сети были последовательно обучены, начинается процесс тестирования. Тестовое изображение разбивается на подобласти. Из каждой подобласти формируется вектор признаков X, который подается на вход узлов первого уровня. Внутри узла рассчитывается вероятность совпадения входного вектора с существующими пространственными центрами у[i]. Интуитивно у[i] может быть представлен как уровень активации соответствующего пространственного центра для данного входного вектора. Вид формулы для расчета у зависит от номера уровня. Для узлов первого уровня имеем у [ г ] = e-| М °2, для узлов других уровней входной вектор представляет собой распределение вероятностей между группами-победителями дочерних узлов
m у [ i ] = ПУ [ C где m - количество дочерних узлов. Найденный вектор у умножается на матрицу смежности P(CIG) для получения выходного вектора распределения вероятности по временным группам X*: nc X* [ j ] = £ у И PCG [i, j ]. i=1 Рис. 5. Примеры правильно классифицированных изображений Узлы верхнего уровня не содержат временных групп. В случае возникновения нового паттерна он автоматически добавляется в группу категории объекта. Таким образом, распределение вероятности по пространственным центрам верхнего уровня служит классификацией изображений по категориям [5]. Результаты тестирования системы. Лучшие результаты на цифровой выборке были получены в случае двухуровневой конфигурации сети: 64 узла на первом уровне, 1 узел на втором. Сеть была обучена на 10 категориях цифр с 30 изображениями для каждой категории. Из каждого изображения формируется видеопоследовательность, состоящая из 100 кадров. Обучающая выборка составляет 30 000 изображений. Вторая выборка [7] состоит из 90 категорий изображений с двумя изображениями для каждой категории, для каждого изображения также формируется видеопоследовательность, содержащая 100 кадров. Обучающая выборка составляет 18 000 изображений. Примеры тестовой и обучающей выборок приведены на рис. 4, 5. Система была протестирована на 300 изображениях цифр. Для зашумленных и искаженных тестовых данных достигнута точность распознавания 97,7 %. Для тестирования картинок использовалось 100 изображений для 40 категорий объектов и 200 изображений для 90 категорий. Точность распознавания для тестовой выборки составила 53,8 и 47,8 % соответственно (см. таблицу). Результаты распознавания цифр и картинок двухуровневой сетью HTM Тип изображений Время обучения, ч Время тестирования, ч Точность распознавания в обучающей выборке, % в тестовой выборке, % Цифры 00:12:09 00:02:30 100 97,7 Картинки (40 категорий) 00:01:18 00:00:11 100 53,8 Картинки (90 категорий) 00:07:58 00:00:59 100 47,8 Снижение точности при распознавании картинок можно объяснить малым количеством обучающих данных, представленных только в двух вариантах масштаба. В результате работы реализована модель память-предсказаниеание в виде двухуровневой сети. Сеть апробирована на задаче распознавания цифр и картинок. Результаты, полученные на широко представленной выборке цифр, оказались положительными (точность распознавания – 97,9 %). Обнаружено, что устойчивость сети зависит от качества и разнообразия представленных для обучения изображений: чем больше и обширнее выборка, тем точнее результат распознавания. На следующем этапе работы предполагается повысить точность распознавания за счет введения в сеть обратной связи, а также саккадных движений.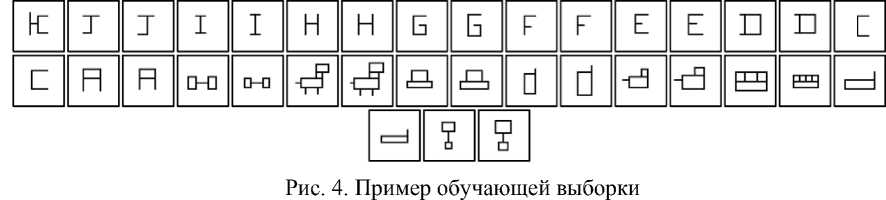

Список литературы Применение модели память-предсказание к решению задачи распознавания образов
- Hawkins J. On intelligence/J. Hawkins, S. Blakeslee. N.Y.: Times Books, 2004. 272 с
- Wolpert D. The lack of a priori distinctions between learning algorithms//Neural Comput. 1996. V. 8, N 7. P. 1341-1390,
- Болотова Ю. А., Спицын В. Г., Фомин А. Э. Анализ и оптимизация модели HTM для распознавания цифр//17-й Междунар. симп. "Оптика атмосферы и океана. Физика атмосферы": Сб. тр. [Электрон. ресурс]. Томск: ИОА СО РАН, 2011. 1 электр.-опт. диск CD-ROM
- Dileep G., George D., Jaros B. The HTM learning algorithms. http://www.numenta.com: сайт компании Нумента. 2006. http://numenta.com/htm-overview/education/ Numenta_HTM_Learning_Algos.pdf http://numenta.com/htm-overview/education/%20Numenta_HTM_Learning_Algos.pdf
- Maltoni D. Pattern recognition by hierarchical temporal memory: DEIS Techn. rep. http://bias.csr.unibo.it: сайт Болонского университета. 2011. http://bias.csr.unibo.it/maltoni/HTM_TR_v1.0.pdf
- Hawkins J., George D. Temporal memory concepts, theory, and terminology. http://www.numenta.com: сайт компании Нумента. 2006. http://numenta.com/htm-overview/education/Numenta_HTM_Concepts.pdf.
- Dileep G. How the brain might work: A hierarchical and temporal model for learning and recognition. numenta.com: сайт компании Нумента. 2007. http://www.numenta.com/htm_overview/education/DileepThesis.pdf


