Применение нейронной сети в решении задач распознавании и классификации космических аппаратов по их оптическим изображениям

Одной из важнейших задач системы мониторинга космического пространства является классификация наблюдаемых космических объектов с целью их отнесения к определенному классу. Одним из наиболее информативных признаков классификации [1] являются оптические изображения, получаемые теми или иными средствами наблюдения [2].

Ручной анализ оптических изображений космических объектов, полученных оптическими инструментами, это очень долгий процесс, требующий кропотливой работы оператора-аналитика, что подтверждает актуальность автоматизации данной задачи [3].

В целях выполнения задач распознавания и классификации изображений наибольшую эффективность применения показывают нейронные сети. Существует большое разнообразие архитектур нейронных сетей, начиная от простейшего перцептрона и заканчивая современными нейросетями с большим количеством нейронов и разнообразных слоев. Широкое распространение получили глубокие нейронные сети [4].

Одними из разновидностей глубоких нейронных сетей являются сверточные нейронные сети, которые при обработке изображений показывают большую эффективность, чем многослойные персептроны. Большое число обучаемых параметров является основным недостатком искусственных нейронных сетей, содержащих только полносвязные слои, в связи с наличием большого числа связей между нейронами. Впрочем, при решении

(оСМИЧЕскйЁ

АППАРАТЫ И

задач, связанных с обработкой изображений, отсутствует необходимость в связях удаленных компонентов изображения друг от друга, поскольку их взаимное влияние фактически сводится к нулю. Применение свертки позволяет учитывать воздействие ограниченного числа примыкающих пикселей изображения, что способствует значительному уменьшению числа обучаемых параметров и увеличению скорости обработки. Свертка позволяет эффективно обнаруживать и запоминать множество признаков в исследуемых изображениях [5]. В подобных алгоритмах машинного обучения признаки выделяются операторами, выделено отдельное специализированное направление исследований - инженерия признаков. Однако, обработка огромных объемов данных оператором занимает большое количество сил и средств, нейронная сеть решит задачу с выделением признаков гораздо оперативнее и качественнее [6].

Содержание методики распознавания и классификации космических аппаратов на основе оптических изображений с применением нейронной сети

Программное обеспечение для реализации методики было написано на языке программирования Python с использованием библиотек tensorflow (программная библиотека открытого доступа для машинного обучения) и keras (откры-

Том 7

тая программная библиотека для настройки, тренировки и оценки качества нейронных сетей).

Отличительной чертой нейронных сетей от математических функций и алгоритмов является необходимость обучения перед применением. Обучение нейронной сети представляет собой процесс определения весов соединений между нейронами в целях приближения требуемой функции с заданной точностью.

На первом шаге был подготовлен набор оптических изображений космических аппаратов для обучения нейронной сети, изображения космических аппаратов были взяты из открытых источников [7]. Всего 576 изображений размером 100x100 пикселей. Выбранное разрешение обусловлено тем, что изображения разных космических аппаратов на снимках очень похожи и нейронной сети потребуется больше количества пикселей с изображением для получения карты признака [8]. Набор изображений был разбит на два каталога: 360 изображений для обучения, 180 изображений для тестирования и 36 (10 % от обучающей выборки) изображений для проверки обучения нейросети (табл. 1).

Кроме того, изображения космических аппаратов были разбиты по трем типам: 1-й тип – КА мониторинга земной поверхности с оптической аппаратурой, 2-й тип – КА мониторинга земной поверхности с радиолокационной аппаратурой, 3-й тип – КА мониторинга земной поверхности с радиотехнической аппаратурой. Пример набора изображений КА первого типа изображен на рис. 1.

Таблица 1

Состав набора изображений для обучения нейросети

Класс	Количество обучающих изображений	Количество тестовых изображений	Количество изображений для проверки
Тип 1	120	60	12
Тип 2	120	60	12
Тип 3	120	60	12

Рис. 1. Пример набора изображений из класса Тип 1

На втором шаге с использованием программного обеспечения были определены выходные значения для нейронной сети (классы, по которым будет осуществляться классификация распознанных изображений): 1-й, 2-й, 3-й тип, и выполнена проверка распределения оптических изображений космических аппаратов по классам.

На третьем шаге была выполнена нормализация входных данных. Это процесс, при котором все поступающие входные данные проходят процесс «выравнивания», то есть приведения к определенному промежутку, в нашем случае [0, 1]. Нормализация позволяет гораздо повысить скорость сходимости алгоритма обучения нейронной сети. Нормализация осуществлена путем опре- деления наибольшего элемента вектора входных данных и деления всех значений на этот элемент:

Unorm = U/ argmaxU, ванный вектор значений. Максимальное значение равнялось 255 – максимальное значение цвета в RGB изображениях.

На четвертом шаге было выполнено создание модели сверточной нейронной сети для обучения, ее архитектура представлена на рис. 2 [9].

где U – трехмерный вектор данных; argmax U – максимальный элемент вектора; U _norm – нормализо-

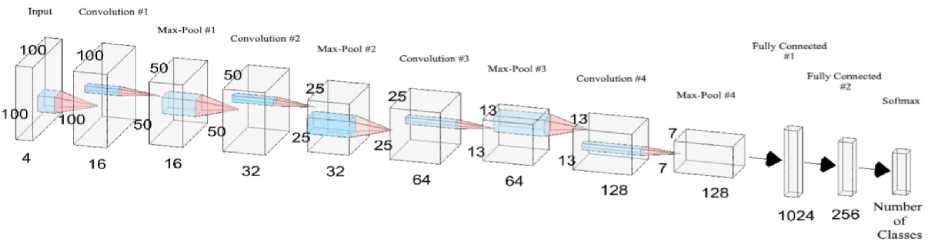
Рис. 2. Архитектура модели нейронной сети

Выбор архитектуры нейронной сети для решения задач распознавания и классификации оптических изображений космических аппаратов обусловлен ее следующими преимуществами:

• •    снижение количества обучаемых параметров и значительное увеличение скорости обучения по сравнению с полносвязной нейронной сетью;

• •    возможность распределения вычислений и реализации алгоритмов обучения сети на графических процессорах;

• •    стойкость к сдвигу позиции объекта во входных данных.

При реализации обучения сверточная нейронная сеть сдвигается по частям объекта. В связи с чем обучаемые признаки не зависят от позиции наиболее важных частей, то есть в каком бы месте на оптическом изображении не находился космический аппарат, нейронная сеть будет его распознавать.

Проанализируем слои созданной архитектуры нейронной сети развернуто.

Input – входные данные с указанием размерности. Conv2D – сверточный слой, имеющий ядро свертки. MaxPooling – сверточный слой, который по принципу действия очень похож на Conv2D, но с тем отличием, что при «движении» происходит не операция умножения, а из части данных выбирается только максимальное значение. Dropout – слой, который предназначен для снижения вероятности переобучения нейронных сетей. Fullyconnected (FC) – полносвязный слой, который состоит из нейронов, каждый из которых соединен со всеми нейронами на предыдущем слое. Основной целью слоя является классификация при помощи создания модели сложной нелинейной функции. ReLU, tanh и Softmax – функции активации, необходимые для формирования выходного сигнала нейронов. Он получается при преобразовании функцией активации взвешенной суммы входных сигналов нейрона. Для активации выходных нейронов сверточных слоев применяется функция ReLU, она выглядит следующим образом:

f x, если x > 0 relu (x) <                 .

[0, если x < 0

Ее основные преимущества – отсутствие ресурсоемких операций, отсутствие затухания градиента при обучении, быстрое обучение. Для активации выходных нейронов полносвязных слоев используется функция активации – гиперболический тангенс ( tanh ), имеющая следующие преимущества: область значений лежит в диапазоне [–1; 1], простое вычисление производной. Для последних слоев, дающих результат классификации в виде прогноза класса, используется функция активации Softmax , она описывается формулой:

_i        n c        _i

^softmax(<) = e / E e‘ , k=1

где xⁱ – i -ое изображение, n_c – количество классов.

Таким образом, функция Softmax преобразует вектор признаков, полученный в нейронной сети для каждого изображения, в вектор, состоящий из чисел, лежащих в диапазоне от 0 до 1, причем сумма всех элементов каждого такого вектора равна единице [10].

По окончанию создания (конструирования) модели нейронной сети с использованием программного обеспечения она получила следующий вид с 5 253 027 параметрами для обучения (рис. 3).

На пятом шаге была выполнена компиляция модели нейронной сети. Компиляция преобразует простую последовательность слоев, которую мы определили, в высокоэффективную серию матричных преобразований в формате, предназначенном для исполнения на графическом процессоре.

Том 7

Рис. 3. Вид модели нейронной сети по окончанию создания (конструирования)

На шестом шаге было выполнено обучение модели нейросети и оценка ее качества. В общем процесс обучения нейросети можно представить в виде, изображенном на рис. 4.

Для реализации обучения нейросети с использованием программного обеспечения необходимо определить количество эпох обучения. Эпоха обучения – это одна итерация в процессе обучения, включающая предъявление всех примеров из обучающего количества и, возможно, проверку качества обучения на контрольном множестве [11].

Обучение нейронной сети проводилось на различном количестве эпох обучения от 10 до 50 эпох, лучшие результаты получения точности предсказаний нейросети получены с 30 эпохами обучения и приведены в табл. 2, обучение нейронной сети с увеличением эпох более 30 не позволило получить точности предсказаний более 0,97.

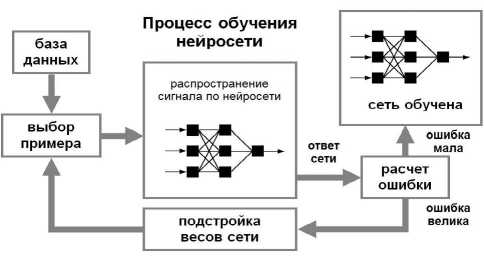
Рис. 4. Процесс обучения нейросети

Таблица 2

Результаты обучения модели нейросети

Номер эпохи обучения	Обучающий набор изображений		Проверочный набор изображений
	Ошибка	Точность	Ошибка	Точность
1	86,82	0,29	4,01	0,36
2	2,58	0,34	1,08	0,38
3	1,08	0,41	1,08	0,38
4	1,08	0,41	1,09	0,36
5	1,08	0,36	1,07	0,36
6	1,05	0,42	1,02	0,52
7	0,99	0,44	0,91	0,50
8	0,94	0,53	0,85	0,63
9	0,87	0,58	0,82	0,55
10	0,79	0,61	0,71	0,66
25	0,12	0,96	0,35	0,77
26	0,10	0,95	0,41	0,86
27	0,12	0,94	0,41	0,80
28	0,13	0,94	0,38	0,80
29	0,08	0,96	0,52	0,80
30	0,07	0,97	0,40	0,83

Результаты обучения модели нейросети: обучающий набор изображений:

• •    точность предсказаний – 30 эпох на 36 % > 10 эпох, 30 эпох на 1 % > 25 эпох;

• •    ошибка предсказаний – 30 эпох на 72 % < 10 эпох, 30 эпох на 5 % < 25 эпох;

проверочный набор изображений:

точность предсказаний – 30 эпох на 17 % > 10 эпох, 30 эпох на 6 % > 25 эпох;

ошибка предсказаний – 30 эпох на 31 % < 10 эпох, 30 эпох на 5 % < 25 эпох.

Далее с использованием программного обеспечения была произведена оценка качества обучения модели нейросети на тестовых данных: ошибка – 0,07, точность предсказаний – 0,97, доля верных ответов на тестовых данных составила 97 %. График оценки доли верных ответов на эпохах обучения и график оценки ошибок на эпохах обучения представлены на рис. 5, 6.

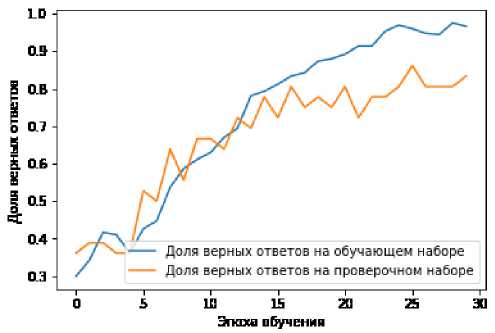
Рис. 5. График оценки доли верных ответов на эпохах обучения программированию, распознаванию и классификации изображений, составляет 96,5–98,5 %.

На седьмом шаге с целью проведения экспериментов по распознаванию и классификации оптических изображений космических аппаратов с использованием программного обеспечения было реализовано:

• •    импорт изображения размером 100×100 пикселей в программную среду;

• •    преобразование изображения из трехмерного в одномерный массив для подачи на вход нейронной сети, таким образом изображения размером 100×100 были преобразованы в массивы, содержащие 10000 элементов;

• •    предсказание классов: Тип 1 – 0, Тип 2 – 1, Тип 3 – 2.

Для демонстрации выполнения седьмого шага методики было выполнено 3 эксперимента по распознаванию и классификации космических аппаратов на основе оптических изображений, результаты экспериментов приведены в табл. 3, 4 и на рис. 7. Обученная модель нейросети успешно справилась с распознаванием и классификацией поданных в нее оптических изображений косми-

ческих аппаратов.

о за ад ш ®

а

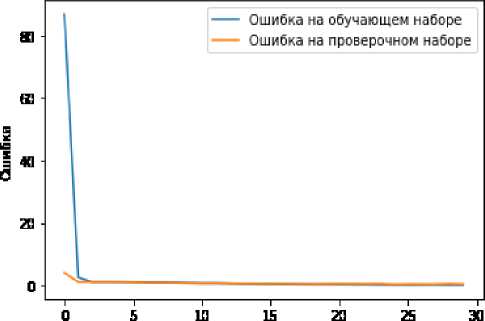
Эпоха обучения

Рис. 6. График оценки ошибок на эпохах обучения

Полученное значение показателя качества обучения модели нейронной сети данной архитектуры достаточно высокое, так как показатели качества обучения похожих моделей нейросетей, доказавших свою эффективность в других экспериментах и международных соревнованиях по о 20 ад ш 81

б

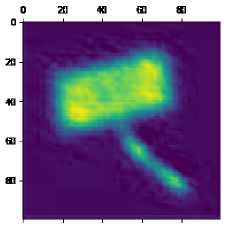
в

Рис. 6. Визуализация машинного зрения признаков в сверточном слое: а – эксперимент № 1;

б – эксперимент № 2; в – эксперимент №3

(шмчесЬё

АППАРАТЫ И

Том 7

Таблица 3

Результаты демонстративных экспериментов

№ п/п	Поданное изображение КА на вход нейросети				Предсказания	Печать результатов
1	° ■ 20 Я 40 Я Я ■ Я Я 0	20      40	Я	я	[0,40846568, 0,30457336, 0,28696108]	Номер класса: 0 Название класса: Тип 1
2	° ■ 20 Я 40 Я Я Я Я Я 0	20      40	Я	я	[0,22658945, 0,32578925, 0,42910256]	Номер класса: 2 Название класса: Тип 3
3	20 Я 40 Я ™ ■ Я Я 0	20      40	Я	я	[0,31252235, 0,45236842, 0,21568552]	Номер класса: 1 Название класса: Тип 2

Для оценки эффективности работы нейросети по распознаванию и классификации изображений космических аппаратов по назначению было проведено дополнительно 30 экспериментов, в том числе

и с подачей на вход нейросети оптических изображений космических аппаратов, отсутствующих в наборе для обучения и тестирования нейронной сети. Результаты экспериментов представлены в табл. 4.

Таблица 4

Результаты проведенных экспериментов

№ п/п	Источник изображения	Результат предсказания	Оценка предсказания	Процент верных ответов
1.	Из набора	0,45236842	Верно
2.	Из набора	0,41235569	Верно
3.	Из набора	0,42589872	Верно
4.	Из набора	0,40253669	Верно
5.	Из набора	0,39256466	Не верно
6.	Из набора	0,42596433	Верно

Окончание таблицы 4

7.	Из набора	0,43389533	Верно	86,6
8.	Из набора	0,48563245	Верно
9.	Из набора	0,42335897	Верно
10.	Из набора	0,45666800	Верно
11.	Из набора	0,41256897	Верно
12.	Из набора	0,35459521	Не верно
13.	Из набора	0,40256984	Верно
14.	Из набора	0,42599842	Верно
15.	Из набора	0,40569871	Верно
16.	Отсутствует в наборе	0,41256842	Верно	66,6
17.	Отсутствует в наборе	0,35458725	Не верно
18.	Отсутствует в наборе	0,40256899	Верно
19.	Отсутствует в наборе	0,39562230	Не верно
20.	Отсутствует в наборе	0,46125600	Верно
21.	Отсутствует в наборе	0,40256980	Верно
22.	Отсутствует в наборе	0,41002568	Верно
23.	Отсутствует в наборе	0,41256982	Верно
24.	Отсутствует в наборе	0,34358974	Не верно
25.	Отсутствует в наборе	0,45236598	Верно
26.	Отсутствует в наборе	0,33569887	Не верно
27.	Отсутствует в наборе	0,45669872	Верно
28.	Отсутствует в наборе	0,41256982	Верно
29.	Отсутствует в наборе	0,45989635	Верно
30.	Отсутствует в наборе	0,33456987	Не верно

Результат предсказаний 30 проведенных экспериментов составил 76,6 %, что на 20,6 % отличается от доли верных ответов тестовых данных, полученных при обучении модели нейронной сети (97,2 %). Хуже результаты были получены с экспериментами оптических изображений, отсутствующих в наборе для обучения и тестирования модели нейронной сети (66,6 %). Полученные результаты в первую очередь связаны с небольшим количеством изображений в наборе для обучения нейронной сети. Для эффективного обучения принято использовать от 4000 изображений до 1,5 миллиона. Вместе с тем экспериментальные результаты даже с 360 оптическими изображениями космических аппаратов позволили успешно обучить нейронную сеть

и реализовать методику распознавания и классификации космических аппаратов.

Заключение

Разработанная методика распознавания и классификации космических аппаратов на основе оптических изображений с применением нейронной сети и ее реализация с применением программного обеспечения на языке программирования Python позволяет повысить оперативность обработки и анализа оптических изображений космических аппаратов. Методика может быть использована при расчете и подготовки данных для информационного обеспечения заинтересованных лиц.