Применение операторов дробного дифференцирования для построения аппроксимативных решений уравнения теплопроводности

Эффективность применения аналитических решений нестационарных задач теплопроводности для целей расчета, анализа, управления и оптимизации в определяющей степени зависит от формы получаемых решений. Во многих случаях точные решения оказываются неэффективными в прикладных задачах вследствие сложности представлений, неудовлетворительной сходимости рядов, трудоемкости вычислительных операций. В статье рассматривается подход к построению приближенных аппроксимационных решений параболических задач, опирающийся на использование операторов дробного дифференцирования.

1.    Постановка задачи

Сущность подхода изложим на примере построения приближенных решений канонической линейной задачи теплопроводности в пластине конечной толщины с граничными условиями 1-го рода д9 = d 29

дт д X ² ’

9 x = 1 = U ( т ) ,                                               (1)

где 9 , т , X - соответственно безразмерные температура, время (число Фурье), пространственная координата, U ( т ) - известная граничная температура.

Решение задачи (1) методом разделения переменных дает представление в виде сходящихся рядов по собственным функциям. Однако такое представление является неэффективным при малых временах вследствие низкой скорости сходимости рядов.

Запишем решение задачи (1) в трансформантах Лапласа в операторной форме [1]

9 ( X ) = W (p , x )U (p),                                 (2)

где

W (P ) =

e V px ₊ e - ^^x

ep

+ e

p

оператор перехода (передаточная функция) от U к θ , символ " " означает трансформанту Лапласа, p – оператор преобразования Лапласа

Переход к оригиналам по времени на основе решения в транформантах (2) (3) приводит к представлениям в виде рядов, эффективных при малых временах (больших p ), но неработоспособных при больших. Они соответствуют внутренним асимптотическим разложениям решения (2) θ i , удобных при p → ∞ .

Построение на основе (2), (3) формальных асимптотических рядов при больших временах (малых p) приводит к сингулярным внешним разложениям θ o , представимым в оригиналах в классах обобщенных функций, использование которых в прикладных решениях затруднительно.

Получаемые таким образом внутренние и внешние разложения не стыкуются друг с другом, не имеют общей области работоспособности, и построение на их основе известными методами сращивания составных асимптотических решений невозможно.

2.    Принцип построения аппроксимативных решений

Сформулируем сущность подхода построения аппроксимативных решений задачи (2), (3) в виде следующих положений:

• 1.    Примем в качестве базовых составляющих приближенных решений N , M конечные суммы внутреннего θ iN и внешнего θ oM асимптотических разложений.

• 2.    На основе θ iN и θ oM сконструируем аддитивную конструкцию

θa =(1-ΩK)⋅θi,N+ΩK ⋅θo,M ,(4)

где Ω K – гладкая (положим K – дифференцируемая) функция-мультипликатор, обеспечивающая сращивание разнородных разложений.

Мультипликатор ΩK ( p) обладает следующими предельными свойствами limΩK(p) = 1 , limΩK (p) = 0 .(5)

p→0

Мультипликатор взвешивает ряды θ iN и θ OM с единичным весом в своих – внутренней и внешней – областях асимптотического описания и монотонно уменьшает их вклад до нуля вне своих областей. В соответствии с этим аппроксимативное решение (4) будет иметь внутренние и внешние асимптотики, соответствующие точному решению (2), (3), плавно сопрягающиеся в промежуточной области.

Построим явную форму мультипликатора Ω K на основе анализа точного решения задачи (3). Видно, что выражение (3), определяющее сущность и закономерности протекания динамических процессов, зависит только от оператора sjp , отвечающего операции дробного дифференцирования степени ½ [2]. В соответствии с этим положим, что для сохранения структурных свойств решений мультипликатор также целесообразно строить как функцию от p . Далее учтем, что решение (3) определяется экпоненциальной зависимостью от дробного оператора вида exp( αJp ) . На основании этого мультипликатор будем конструировать как функцию от exp( γ4 p ), где γ – некоторая константа.

В соответствии с этими двумя вышеизложенными соображениями построим мультипликатор в следующей форме

Ω K ( p ) = exp _K ( γ 4p ) ⋅ exp( - γ 4p ),                        (6)

K zl где expK(z) = ∑ z - многочлен Тейлора степени K для функции exp(z) , γ – численный параметр, l=0 l !

определяемый из условий удовлетворения решения (4) граничным условиям с достаточной степенью точности, соответствующей точности использованных при построении решения (4) внутреннего и внешнего разложений. Очевидно, что асимптотическое поведение мультипликатора (6) удовлетворяет требованиям (5), и структура (6) близко соответствует структуре точного решения (3).

За счет выбора количества членов N,M,K соответствующих рядов θiN , θOM , ΩK и параметра γ получаем возможность конструирования аналитических аппроксимативных решений параболических задач теплопроводности с различной степенью точности и описывающих температурные распределения во всей области определения решений (для те [0, ^], x е [0,1]) с предельным поведением внутренних и внешних асимптотических разложений.

3.    Приближенные решения задачи теплопроводности

Запишем явную форму аппроксимативных решений для оператора (3):

• –    трёхчленное внутреннее асимптотическое разложение

W i2 ( Р , x ) = exp( -P p (1 - x )) + exp( -P p (1 + x ) + exp( -P p (3 - x )) +

+ O (exp( - 3 Р Р ))                                         (7)

• –    двухчленное внешнее асимптотическое разложение

W o ,2 ( p , x ) = 1 + ^Р ( x ² + 1) + O ( p 2 )                            (8)

Видно, что W_{i ,2}( p , x ) и W_{o ,2}( p , x ) являются существенно различными зависимостями, несогласующимися между собой, причем внутреннее разложение (7) имеет так же, как и (3), структуру, соответствующую операциям дробного дифференцирования, а представление (8) – существенно иную, отвечающую операциям дифференцирования в пространствах обобщенных функций.

Используя конструкцию (4) и учитывая различное количество членов во внутреннем 6 iN и внешнем

0 _O M асимптотических разложениях, получим на основе (7), (8) следующие аппроксимирующие решения

W1,1 (p, x) = W1,2 (Pp) = exp(-Pp(1 - x)) + Pp(1 - x) exp(Pp),(9)

W2,1( p, x) = exp(-Pp (1 - x)) + exp(-Pp (1 + x)) - exp(-2Pp),(10)

W2,2 (p, x) = exp(-Pp(1 - x)) + exp(-Pp(1 + x)) - 1 * p( 2   11exp(-2^) ,(11)

W 3,1 ( p , x ) = W 3,2 ( p , x ) = exp( -p p (1 - x )) + exp( -P p (1 + x )) - exp( - P p (3 - x )) -

= Pp (1 - x )exp(-3 Pp).(12)

Видно, что все члены аппроксимирующих решений (9) – (12) имеют аннотированный вид экспоненциальных функций от оператора дробного дифференцирования p и асимптотики аппроксимаций (9)-(12) при p ^ 0 и p ^ ^ совпадают с соответствующими представлениями (7), (8).

Решения (9) – (12) имеют форму, допускающую в большинстве важных для практики случаев переход к стандартным аналитическим функциям в пространстве оригиналов.

Так, для U ( t ) = 1 решения задачи (2), (3) в пространстве оригиналов при W ( p , x ), отвечающих приближениям (9), (10), (11) (12), имеют вид

• 1    - x 1 - x 1

@11(x,т) = 6^(x,т) = erfc(—r) I      exp(-—),(13)

• 2    Vt  Плт4

6*21 (x, т) = erfc(1-Д) + erfc(1+x) - erfc(^),(14)

• 2 Vt      2 VtV

622 (x,t) = erfc(1—x) + erfc(1+x) - erfc(^) —x ^1 exp(- 1),(15)

2V т      2 Vt      Vt  2 ^t3t n X n             г ,1 - xx . г /1+ xx 1 г /3 - xx 1 - x (

631(x,t) = 632(x,t) = erfc(—r) + erfc(—r) - -erfc(—)=- —.=exp(-—).(16)

2V т       2xJ t   2    2 Vt   Пят4t

На рисунке 1 представлены результаты сопоставления точного и приближенных, соответствующих (13) – (16), решений для температурных полей и на рисунках 2, 3 – величины максимальных относительных ошибок для температур и градиентов температур (тепловых потоков). В целом видна удовлетворительная точность аппроксимативных решений и локально-экстремальный по времени характер погрешностей составных разложений.

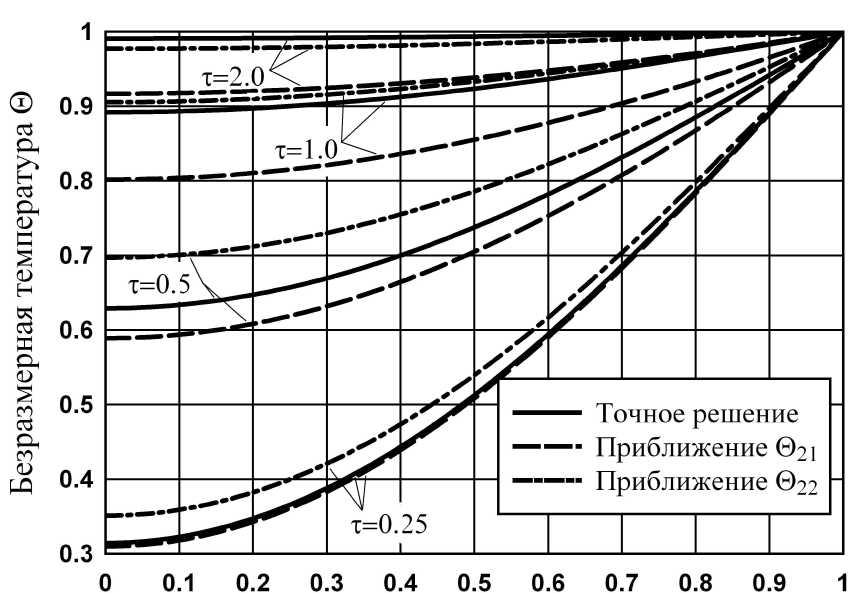
Координата х

Рис. 1. Зависимость температуры от координаты для некоторых моментов времени

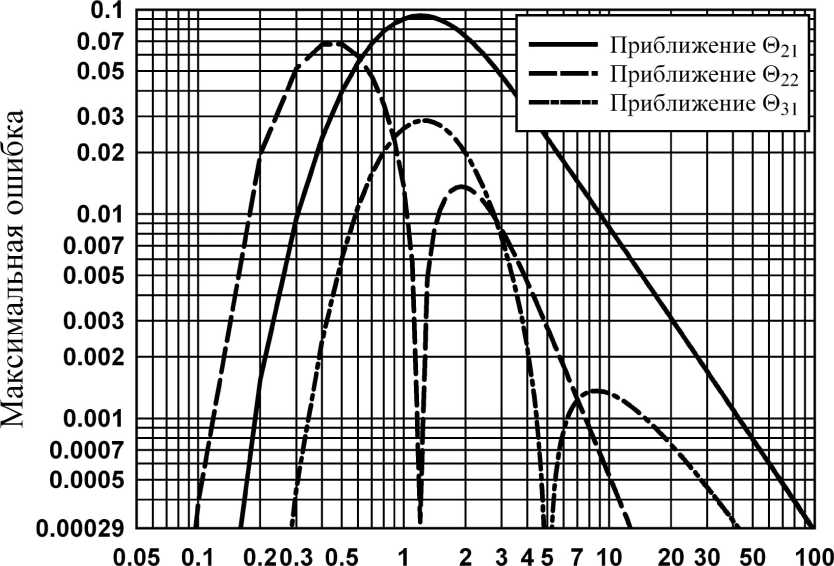
Безразмерное время т

Рис. 2. Зависимость максимальных по координате ошибок расчётов температур от времени

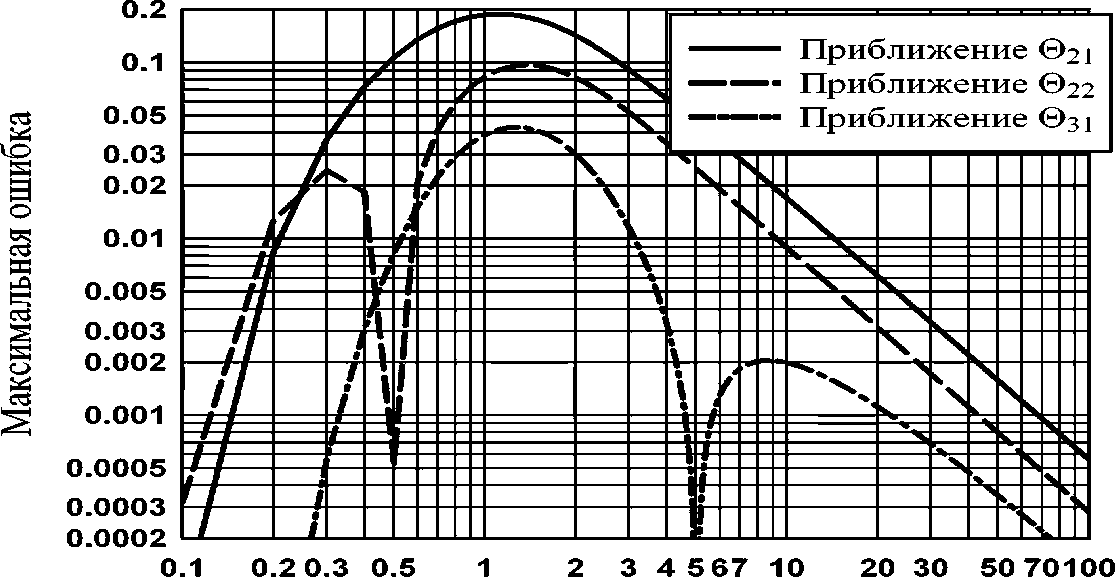
Безразмерное время т

Рис. 3. Зависимость максимальных по координате ошибок расчётов тепловых потоков от времени

При учете дальнейших членов приближенных представлений погрешность аппроксимаций уменьшается.

Заключение

Применение предложенного подхода позволяет получать аналогичные приближенные решения для граничных условий 1, 2 и 3 рода для пластин, цилиндрических тел [3], [4], нелинейных процессов, задач Стефана [5] и иных краевых задач [6].