Применение пакета Fluent для расчета осевой газовой силы, действующей на рабочее колесо центробежного компрессора
Автор: Евгеньев С.С., Зубринкин А.В.
Журнал: Вестник Алматинского технологического университета @vestnik-atu
Рубрика: Международная научно-техническая конференция Казахстан-Холод
Статья в выпуске: 1 (97), 2013 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/140204629
IDR: 140204629 | УДК: 621.55
Текст статьи Применение пакета Fluent для расчета осевой газовой силы, действующей на рабочее колесо центробежного компрессора
Приведена последовательность расчета осевой газовой силы, действующей на рабочее колесо центробежного компрессора, с использованием результатов численного моделирования течения в боковых зазорах около дисков колеса по пакету Fluent.
Центробежные компрессора (ЦК) широко применяются при добыче нефти и газа, в нефтехимии, химии, металлургии. Эффективность указанных отраслей во многом определяется надежностью и экономичностью этих машин. При этом важнейшим фактором, влияющим на надежность и экономичность, являются осевые газовые силы, действующие на рабочие колеса (РК) ротора, на снижение и уравновешивание которых расходуется до 10% полезной мощности. Значительный вклад в решение этой важной проблемы внесли работы Риса В.Ф., Дена Г.Н., Шершневой А.Н., Шнеппа В.Б. и др. Методы расчета, снижения и уравновешивания осевых сил в ЦК, широко используемые на практике, представлены также в работе [1]. Дальнейшее совершенствование методов расчета осевых сил в ЦК требует более глубокого изучения расходного течения в боковых зазорах разных форм между дисками РК и корпусом, граничных условий, влияющих на распределение давления, осевую силу и мощность трения дисков РК.
Целью настоящей работы является создание инженерного метода расчета осевых газовых сил, действующих на РК ЦК, основанного на численном моделировании течения в боковых зазорах между дисками РК и корпусом с помощью пакета Fluent (версия 6.2.16) с последующей экспериментальной проверкой.
В качестве объекта исследования рассмотрена первая ступень многоступенчатого ЦК для сжатия природного газа (рис.1). Исходные известные геометрические и газодинамические данные на расчетном режиме, необходимые для расчета осевых сил, показаны в таблице 1. Особенностью данной реальной ступени являются умеренные окружные скорости РК (u 2 =233 м/с) и, соответственно, низкие значения отношения давлений (πк=1,285) и числа Маха (Мu=u 2 /a0=0,533).
Численное моделирование течения в боковых зазорах около покрывного диска (течение к оси) и основного диска (течение от оси) РК с применением пакета Fluent выполнено [2] для турбулентного осесимметричного течения. Среду считали несжимаемой ввиду незначительной степени изменения давления в этой области, что доказано экспериментами на воде и воздухе [1,3]. Параллельные поверхности дисков РК и корпуса считали точеными с одинаковой шероховатостью. Использована модель турбулентности k–εRNGSWF.
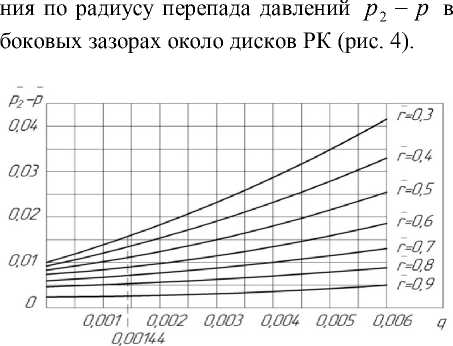
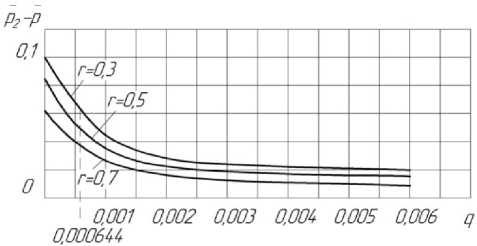
Результаты численного моделирования течения с применением пакета Fluent, в виде зависимостей р 2 - р = f ( г , q ) и N = f ( q ), необходимых для расчета осевых сил при значениях r =0,3…1, S =0,03, q=0…0,006, C u 2 =0.72, реальных для рассматриваемой ступени, показаны на рис.2 и рис.3.
Для дальнейших расчетов необходимы параметры за РК на радиусах r 2 (по ширине b 2 ) и r л с учетом влияния характера течения в боковых зазорах и утечек через лабиринтные
е 2 = 1 + ( к - 1 ) М И ^- П
к
η пол к - 1
- 1
L П пол J
.
Предварительно, по данным [3] для РК с вл 2 =650 и b 2 = 0,05...0,06 принимали Ω=0,6.
Теоретический коэффициент напора РК без закрутки на входе в РК (С1u=0)
С и 2 =
ψ
П пол (1 + в пр + в тр )
где β пр
q • е 2
π Ф 0 τ 2
β тр
,
N nOK + N och
π Ф 0 С u 2 τ 2
уплотнения покрывного (на r л ) и основного (на Г л = г в ) дисков РК. Перечень параметров и окончательных их значений, рассчитанных последовательными приближениями по известным формулам [3], и данным моделирования по пакету Fluent, показан в таблице 2. Рассмотрим порядок их определения.
Коэффициент расхода РК на выходе
Ф 2 = ФТ"
4 b 2 ε 2
, где:
Предварительно значение С u 2 находили по формуле Стодолы [3]
π
Си2 = 1Sin^2 - Ф2ctg^2 z2 , а величины N пок и Nосн – по рис. 3, задавшись приближенными значениями q=0,003 для покрывного диска (течение К оси) и q=0,0015 для основного диска (течение ОТ оси).
Далее находили остальные величины в первом приближении:
Q = 1 - ф 2 + Си 2 - ф 0 ;
" " 2 • ^_ ’
M t 0 - 2 =^ ( Tk - T 0Y ;
Т = Т +М • 12 '0 + ^ t 0 - 2 ’
η пол
р 2 = р 0
I t ') n
V T 0 7
nk
1 k - 1
; P 2 = P 0
Tt
V T 0 7
nk - 1
;
ε 2
= Pl
ρ 0 ,
где
nk
= f П 0 - 2 n k - 1 k - 1
Для определения значения p2 - рл для данного rл использовали результаты моделирования течения в боковых зазорах по пакету Fluent для течения К оси и ОТ оси, показанные на рис. 2. При rл =0,623 и заданного q=0,003 для покрывного диска находили p2 - рл (рис. 2а) и далее при p2 = р2 / р2 • и2 величину рл. По формуле
Стодолы для безразмерного расхода через лабиринтное уплотнение покрывного диска определяли значение q. Аналогично для основного диска при г л = г в = 0,3 и заданного q=0,0015 находили р2 - рл (рис. 2б) и далее pл . По формуле Стодолы для безраз- мерного расхода через уплотнение основного диска q = 2пало • ГлЗл
рк - рл
ρ zo • Рк • — ρk
q = 2.na m • Г л З л
р л - р 0
V z n • Р л
определяли значения q.
Далее рассчитывали все величины в таблице 2 для следующих приближений.
Расчеты показывают достаточность 3-х приближений, когда последующие значения р 2 , Т 2 , ρ 2 , ε 2 , С u 2 , рл и q отличаются от предыдущих не более чем на 1…2 %.
По окончательным величинам q для покрывного и основного дисков по рис. 2
определены значения p 2 - p для разных r и
Т пок = А - Б = π (1 - r л ) р 2
построены эпюры давления по радиусу, показаны экспериментальные данные [2] и известная зависимость для случая ω Г = 0,5 (рис. 4). В результате рассчитаны безразмерные осевые силы, действующие на покрывной Т пок и основной Т осн диски по выражениям
- 2 π ∫ ( р 2 - р ) rd r , rл
Т осн = А ′ - Б ′ = π (1 - r л
) р 2 - 2 π ∫ ( р 2 - р ) rdr ,
rл=rв и суммарная осевая сила, действующая на РК, в размерном виде
Т ∑ = ( Т осн
- Т пок ) ρ 2 u 2 r 2 - TВХ - RВТ ,
где ТВХ = р 0 π ( rл 2 - rВ 2 Т ) – осевая сила на входе РК,
G 2
RВТ = GC 0 = 2 2 – реакция втекания потока в РК.
ρ 0 π ( r 0 - rВТ )
Результаты расчетов этих величин показаны также в таблице 2.
Таким образом, определение осевой силы, действующей на РК ЦК, выполняется последовательно с использованием: известных газодинамических параметров ступени и геометрии боковых зазоров около дисков РК; зависимостей на рис.2 и рис.3, полученных в результате численного моделирования течения в боковых зазорах по пакету Fluent; точных расчетов параметров за РК (р2, Т2, ρ2, С u 2 ), давлений рл и расходов q; распределе-
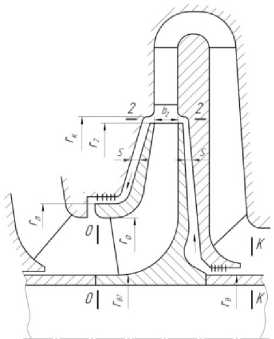
Рисунок 1 - Схема ступени ЦК.
а)
Рисунок 2 - Зависимости p 2 - p = f ( r , q ) для течения к оси (а) и от оси (б) в боковых зазорах РК ( S = 0,03; С u 2 = 0,72; Re u = 2,35 ⋅ 10 6).
б)
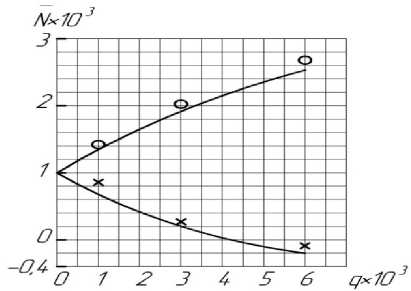
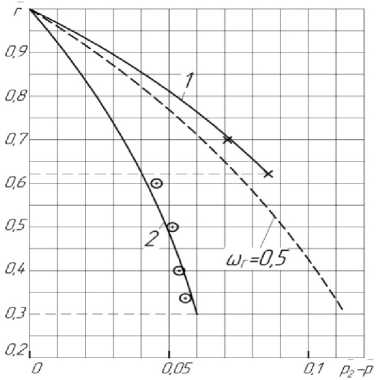
Рисунок 4 - Зависимости p 2 - p = f ( r ) : 1 – покрывной диск, q=0,00144; 2 – основной диск, q=0,00065 ( S = 0,03; С u 2 = 0,72; Re u = 2,35 ⋅ 106 ) х, о – экспериментальные точки [2].
Рисунок 3 - Зависимости p 2 - p = f ( r , q ) для течения к оси (а) и от оси (б) в боковых зазорах РК ( S = 0,03; С u 2 = 0,72; Re u = 2,35 ⋅ 10 6).
Таблица 1
|
Геометрические величины |
||||||||||||||||||||
|
r 2 |
b 2 1 |
r 0 1 |
r л 1 |
r ВТ |
r B 1 |
S |
z 2 |
τ 2 |
z п |
z 0 |
α лп |
α ло |
β л2 |
|||||||
|
мм; см. рис. 1. |
20 |
0,98 |
5 |
5 |
1,2 |
1,2 |
650 |
|||||||||||||
|
420 |
50 1 |
252 |
262 |
126 |
126 |
12,5 |
||||||||||||||
|
z 2 – число лопаток РК; τ 2 – коэфф-т стеснения площади выхода РК; z п , z 0 , α лп , α ло , – число гребней и коэфф-ты расхода лабир. уплотнений пок. и осн. дисков; β л2 – угол лопаток РК на r 2 |
||||||||||||||||||||
|
Парамет |
ры ступени компрессора |
|||||||||||||||||||
|
к |
R Г Дж/кгК |
р 0 Па |
Т 0 К |
z |
ρ 0 кг/м3 |
υ 0 м2/с |
R eu |
u 2 м/с |
Mu |
|||||||||||
|
1,313 |
513 |
5,4 ⋅ 106 |
283 |
0,89 |
41,79 |
0,27∙10-6 |
3,46∙108 |
233 |
0,533 |
|||||||||||
|
Ф 0 |
ψ |
η пол |
η 0-2 |
πк |
р к Па |
Т к К |
G кг/с |
С 0 м/с |
С ϕ 0 = 0 u 2 |
|||||||||||
|
0,12 |
0,6 |
0,81 |
0,87 |
1,285 |
6,94∙106 |
304,6 |
647,2 |
103,4 |
0,443 |
|||||||||||
|
к – показатель адиабаты; R Г – газовая постоянная; р 0 , Т 0рк Т к , – давления и температуры на входе и выходе ступени; z – коэфф-т сжимаемости; ρ 0 , υ 0 – плотность и кинематическая вязкость на входе; R eu , M u – числа Рейнольдса и Маха; u 2 – окружная скорость РК; Ф 0 = 4 V 0 / πD 2 2 ⋅ u 2 – усл. коэфф-т расхода; ψ = Hпол / u 2 2 – коэфф-т напора ступени; η пол , η 0-2 – политр. КПД ступени и РК; π к – отнош-е давлений ступени; G – массовый расход; С 0 – скорость газа на входе; |
||||||||||||||||||||
Таблица 2
|
Величины, рассчитанные с применением пакета Fluent |
|||||||||||||||||||
|
φ 2 |
С u 2 |
β пр |
β тр |
N ⋅ 103 пок |
N ⋅ 103 осн |
Ω |
∆ t 0 - 2 К |
Т 2 К |
р 2 Па |
||||||||||
|
0,444 |
0,73 |
0,00438 |
0,00755 |
0,5 |
1,3 |
0,648 |
14,0 |
297 |
6,44 ⋅ 106 |
||||||||||
|
ρ 2 кг/м3 |
ε 2 =р 2 /р 0 |
р 2 = р 2 / ρ 2 u 2 |
Т ⋅ 10 - 5Н ВХ |
R ВТ ⋅ 10 - 5 Н |
Т ∑ ⋅ 10 - 5 Н |
||||||||||||||
|
47,49 |
1,136 |
2,497 |
8,94 |
0,67018 |
1,01375 |
||||||||||||||
|
Покрывной диск |
Основной диск |
||||||||||||||||||
|
р 2 - рл |
р л |
q |
A |
Б |
Т пок |
р 2 - р л |
р л |
q |
А ′ |
Б ′ |
Т осн |
||||||||
|
0,885 |
2,412 |
0,00144 |
4,797 |
0,0844 |
4,712 |
0,06 |
2,437 |
0,000644 |
7,135 |
0,0868 |
7,048 |
||||||||
|
φ 2 – коэфф-т расхода; β пр , β тр – относит. потери на утечки и трение; N = N / ρ 2 r 2 5 ω 3 – коэфф-т мощности трения диска; q = Gy / ρ 2 r 2 2 ⋅ u 2 – безразмерная утечка через лабир. уплотнение. |
|||||||||||||||||||
Список литературы Применение пакета Fluent для расчета осевой газовой силы, действующей на рабочее колесо центробежного компрессора
- Евгеньев С.С. Разгрузка осевых сил с целью повышения надежности турбомашин//Химическое и нефтяное машиностроение. -1995. -№11. -С.15-21.
- Евгеньев С.С., Зубринкин А.В. Численный и экспериментальный анализ течения в боковых зазорах между рабочим колесом и корпусом центробежного компрессора//Компрессорная техника и пневматика. -2012. -№6. -С.36-39.
- Ден Г.Н. Механика потока в центробежных компрессорах. Л.: Машиностроение, 1973. -272 с.


