Применение пакета прикладных программ для решения задач, связанных с очисткой почвы от нефти и тяжелых металлов посредством биосурфактанта

В последние годы с целью ликвидации последствий углеводородных загрязнений почвы все чаще применяют эффективные и экологически безопасные технологии биологической очистки (биоремедиации), основанные на использовании микроорганизмов и продуктов их жизнедеятельности, в частности биогенных поверхностно-активных веществ (биосурфактантов).

В лаборатории алканотрофных микроорганизмов Института экологии и генетики микроорганизмов УрО РАН получены высокоактивные биосурфактанты, синтезируемые бактериями рода Rhodococcus . Полученные биосурфактанты с высокой нефтеэмульгирующей и нефтеотмывающей способностью успешно применяются в процессах биоремедиации загрязненных почвогрунтов [1]. Лабораторные

Куюкина Мария Станиславовна, д.б.н., в.н.с. лаборатории алканотрофных микроорганизмов, профессор кафедры микробиологии и иммунологии, Пермь

Ившина Ирина Борисовна, д.б.н., профессор, чл.-корр. РАН, зав. лабораторией алканотрофных микроорганизмов, профессор кафедры микробиологии и иммунологии, Пермь

Костина Людмила Викторовна, к.б.н., инженер лаборатории алканотрофных микроорганизмов, Пермь Осипенко Михаил Анатольевич, к.ф.-м.н., доцент кафедры теоретической механики, Пермь Няшин Юрий Иванович, д.т.н., профессор, зав. кафедрой теоретической механики, Пермь исследования показали, что Rhodococcus-биосурфактант способствует эффективной десорбции нефтяных углеводородов [6, 7] и солей тяжелых металлов [2, 3, 8, 9] из загрязненной почвы.

Для подбора эффективных приемов и создания оптимальной схемы биоремедиации необходимо построение биомеханических и математических моделей, адекватно описывающих процесс очистки загрязненного почвогрунта от нефти и тяжелых металлов с помощью биосурфактанта. Ранее авторами построены согласующиеся с экспериментальными данными биомеханические модели: модель проникновения нефти в почве, модель проникновения биосурфактанта в нефтезагрязненной почве, модель проникновения биосурфактанта в почве, загрязненной солями тяжелых металлов [2, 4].

Прогнозное математическое моделирование – эффективный инструмент современной экологической биотехнологии, направленный на адекватное описание и прогнозирование природных процессов в условиях техногенного воздействия. В частности, построение математических моделей позволяет находить оптимальное решение, адекватное описанию процесса загрязнения почв нефтью и нефтепродуктами, прогнозирование последствий нарушения почвенных процессов и выбор оптимальной стратегии биоремедиации [4]. Следует отметить, что очищение почвы от загрязняющих веществ (углеводородов нефти) – процесс комплексный, в котором участвуют физические, химические и биологические факторы. При этом действие всех факторов взаимообусловлено и синергично. Исследование сложных механизмов биоремедиации требует создания пакета прикладных программ на основе биомеханических и математических моделей, описывающих процессы очистки почвы от нефти и солей тяжелых металлов под действием биосурфактантов.

В настоящей работе представлен пакет прикладных программ, разработанный на основе биомеханических и математических моделей процесса фильтрации Rhodococcus- биосурфактанта в нефтезагрязненной почве и почве, загрязненной солями тяжелых металлов.

Описание пакета прикладных программ

Пакет прикладных программ «Очистка загрязненной нефтью и тяжелыми металлами почвы с помощью биосурфактанта» (рис. 1) позволяет решать следующие биомеханические задачи: вычисление времени отмывания биосурфактантом загрязненной нефтью почвы, находящейся в накопительном резервуаре; вычисление коэффициента сопротивления k фильтрации биосурфактанта в почве, загрязненной солями тяжелых металлов, прогнозирование эффективности биоремедиации. Пакет состоит из трех блоков, функционирование которых описано ниже.

Блок «Расчет времени отмывания биосурфактантом загрязненной нефтью почвы, находящейся в накопительном резервуаре» предназначен для определения времени прохождения заданного количества биосурфактанта в загрязненной нефтью почве, находящейся в накопительном резервуаре, а также для определения средней скорости вытекания биосурфактанта из накопительного резервуара.

Загрязненный нефтепродуктами почвогрунт находится в резервуаре, имеющем форму прямоугольного параллелепипеда (рис. 2). На верхней границе (открытая поверхность) давление атмосферное; на дне находится вакуумный насос, который откачивает биосурфактант под давлением, равным атмосферному; боковые стенки и часть дна ( l ₀ ≤ x ≤ l ₁ ) – непроницаемые поверхности.

Открытая поверхность орошается биосурфактантом. В нефтезагрязненном почвогрунте происходит фильтрация биосурфактанта, осуществляющаяся в два этапа.

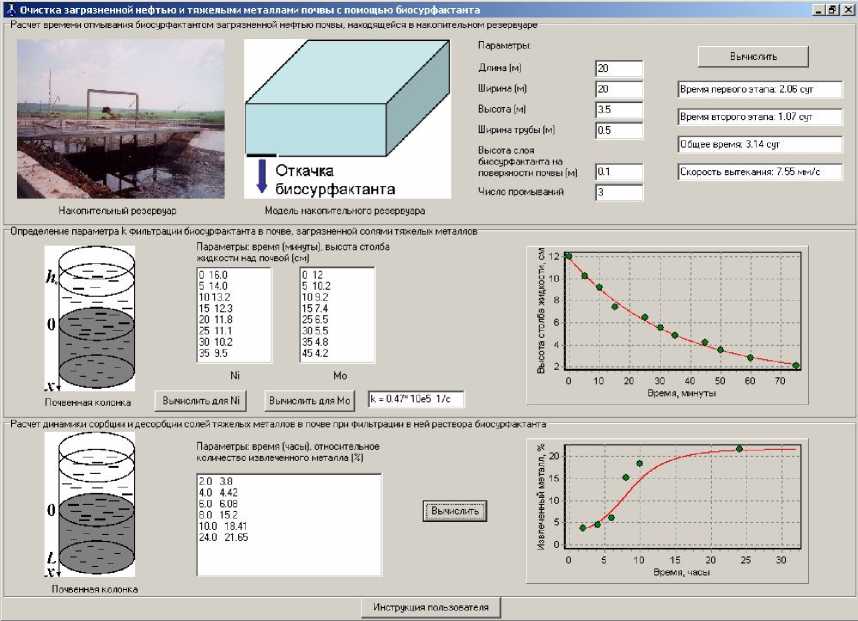
Рис. 1. Пакет прикладных программ «Очистка загрязненной нефтью и тяжелыми металлами почвы с помощью биосурфактанта»

На первом этапе имеется фронт проникновения биосурфактанта. На втором этапе, после достижения биосурфактантом дна резервуара, происходит его откачивание через трубу с помощью вакуумного насоса.

Процесс фильтрации описывается уравнениями безынерционного течения идеальной несжимаемой жидкости под действием силы тяжести, объемной силы сопротивления, пропорциональной скорости, и силы сопротивления, сосредоточенной на фронте проникновения и зависящей от скорости. Для решения использованы математические модели: задача Коши для обыкновенного дифференциального уравнения и краевая задача для уравнения Лапласа в прямоугольнике. А именно, на первом этапе фильтрации gh0/a + (g - kdl(t)/dt) l(t) - f (dl(t)/dt) = 0, где g – ускорение свободного падения, h0 – толщина слоя биосурфактанта на открытой поверхности почвогрунта, a - пористость почвогрунта, k - коэффициент сопротивления при фильтрации, l - глубина проникновения биосурфактанта, f (•) -зависящая от скорости сила сопротивления, сосредоточенная на фронте проникновения биосурфактанта. На втором этапе фильтрации

A p (x, y, z ) = 0, где A - оператор Лапласа, p - давление биосурфактанта. Краевые условия для давления на границе резервуара ap/axx=0 = ap/axx=l = ap/ayy=0 = ap/ayy=4 = 0,    ap/az|z=0 = -рg при y>lо, где 11 - ширина резервуара, 12 - длина резервуара, 10 - ширина трубы, р -эффективная плотность биосурфактанта. Так как на открытой поверхности резервуара

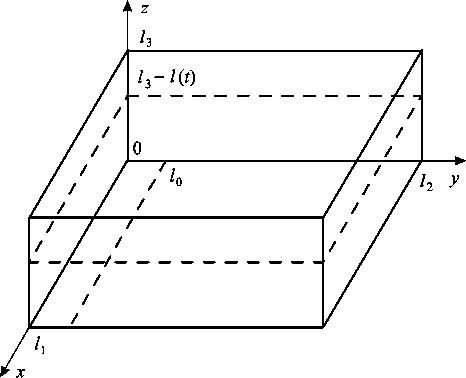
Рис. 2. Модель резервуара с загрязненным почвогрунтом

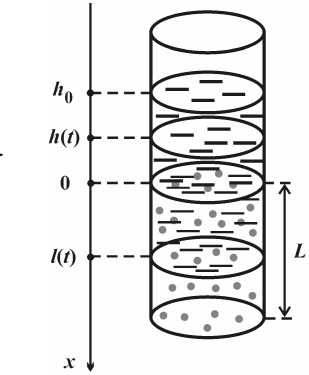
Рис. 3. Схематическое изображение почвенной колонки

имеется слой биосурфактанта толщиной производится вакуумным насосом, то

h ₀ , а откачивание биосурфактанта

p

_z = l₃ = p 0 ⁺ P 0 gh 0 ,     p|

_z = ₀ = ⁰ при y <  ^l 0 ,

где l3 - высота резервуара, p0 - атмосферное давление, p0 - плотность чистого биосурфактанта. Последнее условие заменяется на приближенное dpldAz=0 = p(kU—g) при y < l0, где U следует найти из соотношения

J( l ¹ J 0⁰ p ⁽ x , y , ⁰⁾ dxdy = ^0.

Величина U есть средняя (по области 0 <  x <  1 1 , 0 <  y <  1 ₀) скорость откачивания биосурфактанта. Решение задачи для p имеет вид [5]

p ⁽ y , Z ) = p о +P о gh о +P g V

• nnlo sin

-

kUl о )

l ₂

( 1 3 - Z )

-

—

2 p kUl ₂ n ²

E ra          l-)       n n ( l₃

2sh n=1       П nll n2ch    32

l ₂

где

U =

'a +

l ₂

—

z)    nny cos , l2 ,

\

^ + Д pa- + gh

g

k 2 l 2 ^{2 n 3 l} 0 ^l 3

kl 31 P

Era n=1

a )

1 • 2 ⁿnk

3 sin

n

l ₂

, nnL th 3

l ₂

.

Блок «Определение параметра k фильтрации биосурфактанта в почве, загрязненной солями тяжелых металлов» предназначен для определения k – коэффициента сопротивления со стороны среды при фильтрации биосурфактанта в почве на основе экспериментальных данных по фильтрации биосурфактанта в почве, загрязненной солями тяжелых металлов.

Эксперимент проводится в модельных почвенных колонках. Почва, загрязненная солями тяжелых металлов (никеля и молибдена), находится в стеклянной колонке. Одна колонка схематично показана на рис. 3. Здесь h 0 – высота столба налитой сверху жидкости (водного раствора Rhodococcus -биосурфактанта), l – глубина проникновения жидкости в почву, t – время; поверхность почвы отвечает координате x = 0. Параметры колонок - диаметр d и высота L слоя почвы (рис. 3).

Процесс фильтрации биосурфактанта в модельной почвенной колонке описывается уравнениями безынерционного течения идеальной несжимаемой жидкости под действием силы тяжести и объемной силы сопротивления, пропорциональной скорости. Высота h столба жидкости как функция времени оказывается согласно теории различной для солей никеля и молибдена, а именно для солей никеля h (t) = a1 - a 2t, а для солей молибдена

h(t) = a3 exp(-a4t) + a5, где один из параметров ai (в каждом случае) выражается через k. Обработка экспериментальных данных методом наименьших квадратов позволяет найти этот параметр и, следовательно, коэффициент k.

Данный блок состоит из полей для ввода параметров (для каждого металла предназначено отдельное поле), полей для вывода результата и диаграммы, на которой отображаются экспериментальные точки и теоретическая кривая, построенная по результатам расчета.

Блок «Расчет динамики сорбции и десорбции солей тяжелых металлов в почве при фильтрации в ней раствора биосурфактанта» предназначен для прогнозирования эффективности биоремедиации. Данный блок состоит из поля для ввода параметров, поля для вывода результата и диаграммы, на которой отображаются экспериментальные точки и теоретическая кривая, построенная по результатам расчета.

Процессы сорбции и десорбции солей тяжелых металлов изучались в модельных почвенных колонках. Наблюдалась динамика извлечения солей никеля и молибдена из почвы под действием водной эмульсии Rhodococcus -биосурфактанта (4 г/л, штамм Rhodococcus ruber ИЭГМ 231), синтетического биосурфактанта Tween 80 и дистиллированной воды [2]. Загрязненная солями тяжелых металлов модельная почва находилась в стеклянных колонках (см. рис. 3). Выше нулевой отметки находилась жидкость, ниже нулевой отметки – загрязненная почва и проникшая в почву жидкость; поверхность почвы отвечает координате x = 0.

Количественное определение ионов никеля и молибдена, десорбированных из почвы в водную фазу, проводилось с помощью спектрофотометра диметилглиоксимным и роданидным методом, соответственно. Эффективность процесса десорбции с течением времени t выражалась в массовой доле ц ( t ) десорбированной соли от общего начального количества сорбированной соли.

Для решения использована математическая модель: начально-краевая задача для уравнения переноса. Математическая модель очистки почвы от солей тяжелых металлов основана на уравнениях материального баланса, описывающих десорбцию тяжелых металлов от почвы и повторную сорбцию их к почве:

5т/ 5t + V 5т/ 5x = an - в m,

■5п/ 5t = -an + вm, x > 0, t > 0, nt=0 = n0, mt=0 = 0, mx=0 = 0, где x – координата, отсчитываемая вдоль колонки, t – время, m – концентрация десорбированной соли, n - концентрация сорбированной соли, а - коэффициент сорбции, в - коэффициент повторной сорбции, V - скорость течения жидкости в загрязненной почве, n0 – начальная концентрация соли в почве. Решение записанной задачи имеет вид [5]

а n 0 .                     _х а n 0

m ( x , t ) =----- ( 1 - exp( - ( а + в ) t ) )-- exp( -в x I V ) x

а + в                   а + в

'0, 0 < t < xV, x<

t - XV

J exp(-ат)10(2^авxт/V)(а + вexp(-(а + в)(t-x/V-т)))dt, t - x/V,

, 0

n ( x , t ) = n ₀

1-- " +----- exp( - ( а + в ) t )

^а+ва+в      J

-

ав n 0

-----exp( -в x IV ) x а+в

'0, 0 < t < x/V, x<

t - x/V                      ___________

J exp( -ат ) 1 ₀ ( 2^ ав x т/ V ) ( 1 - exp ( - ( а + в ) ( t - x/V -т ) ) ) d t , t - x/V ,

, 0

где I0 – модифицированная функция Бесселя. Экспериментально измеряемая зависимость ц(t) выражается следующим соотношением:

V Ц * f

ц ( t ) =-----I m ( L , т ) d т ,

Ln 0 ₀

где L - длина колонки, ц* = lim ц(t). Тогда а V ц*

Ц⁽ t ) = 7---777

( а + в ) L

'0,0 < t

1 - ехр(-(а + в) t)

t---“ а + в

t - x/V exP (-вLV ) J Ц(t, t) dт, t - LV , 0

где

Ц(t, т) = ехр(-ат)1₀(2^авLт/V) а(t - L/V -т)+—^[l - exP (-(а + в) (t - L/V -т))] .

Заключение

В настоящей работе представлен пакет прикладных программ «Очистка загрязненной нефтью и тяжелыми металлами почвы с помощью биосурфактанта». Описаны основные блоки, составляющие представленный пакет прикладных программ, биомеханические и математические модели, на основе которых осуществляется решение задач в каждом из блоков пакета программ.

Благодарности

Исследования поддержаны грантами Министерства образования и науки РФ (ГК 16.518.11.7069, 2011-1.3-513-082) и Программы Президиума РАН “Молекулярная и клеточная биология”.