Применение параболического сплайна для анализа распределения населения по доходам

Вопросам изучения проблем неравенства населения различных регионов России и мира посвящена весьма обширная литература [1-4 и др.]. Количественная оценка степени расслоения населения по доходам опирается на теоретическую кривую Лоренца, которая наглядно иллюстрирует распределение доходов и строится на основе анализа соответствующей статистической информации. К наиболее часто используемым количественным показателям (индикаторам) неравенства относятся индексы Джини, Пальмы, Гувера, коэффициенты фондов и др. Особое место среди количественных показателей неравенства занимает коэффициент Джини, который остается одним из основных индикаторов неравенства.

В результате многочисленных исследований установлено, что количественные оценки показателей неравенства на основе использования теоретических функции распределения и кривой Лоренца существенно зависят от выбора функции распределения и методики оценки точности аппроксимации [5-8 и др.]. Понятно, что выбор функции распределения зависит от конкретной статистической информации. Тем не менее, используемая Росстатом методика расчета показателей дифференциации населения по уровню доходов опирается на использование логнормального распределения [9]. Обоснование такого выбора и соответствующие комментарии можно найти в работах [5, 10, 11]. Так, в работе [11] читаем: «Хорошо известно, что распределение доходов описывается логнормальным распределением». Однако существуют работы, в которых использование функций, опирающихся на нормальное распределение, ставится под сомнение. Приведем мнение А.И. Орлова: «…широко распространена вера в то, что статистические данные часто подчиняются нормальному распределению. Математики думают, что это – экспериментальный факт, установленный в прикладных исследованиях. Прикладники уверены, что математики доказали нормальность результатов наблюдений. Между тем анализ конкретных результатов наблюдений, в частности, погрешностей измерений, приводит всегда к одному и тому же выводу – в подавляющем большинстве случаев реальные распределения существенно отличаются от нормальных» [12].

Целью нашего исследования является эмпирическая проверка гипотезы о возможности использования логнормальной функции в качестве адекватной модели распределения населения по доходам. В качестве основного инструментального средства исследования используется метод сплайн-функций [13, 14]. Значения свободных параметров параболического сплайна определялись из решения задачи о минимизации интегральной гладкости функции распределения при выполнении условия о ее монотонном возрастании. В качестве информационной базы исследования использовались статистические данные о распределении заработной платы работников организаций РФ в 2019 г.

1.    Задача построения функции распределения

При анализе неравенства в распределении доходов населения предполагается, что все население ранжировано в порядке возрастания доходов. Ниже используются следующие обозначения: x - величина денежного дохода; x - значение минимального денежного дохода населения; y - доля населения с доходами не более x в общей численности населения (кумулятивная доля населения); z - доля совокупных доходов населения, доходы которых не превышают x , в совокупном доходе всего населения (кумулятивная доля дохода). Упомянутая выше функция логнормального распределения может быть записана так:

x

F ( x , а , а ) = J f ( t , а , а ) dt , 0

где

^{f (} x , a , a ) =

ax Jin

exp

V

(In x - In a )²

2a   ,

С формальной точки зрения для определения параметров а и а кумулятивной функции распределения (1) на основе статистических данных вида ( x_k, у_к ) , где вектор параметров, x_k и у_к — значения переменных x и y , к = 1,2,..., N , требуется решить задачу минимизации некоторой функции W ( а ) , характеризующей степень близости графика теоретической функции от эмпирических точек А_к ( Хк , У к ) . Одной из таких функций является следующая часто используемая функция:

N

W ( а ) = v 2 ( F ( x k , а ) - У к > 2 - (3) N к = 1

Однако вместо решения задачи минимизации функции (3) часто используется следующий прием: параметры a и а функции распределения (1) определяются по двум числовым характеристикам распределения, например по среднему и медиане, или по моде и медиане, или по среднему и среднеквадратическому отклонениям, или по моде и максимальному значению функции плотности (2). «Таким образом, для их вычисления уже не требуется знания всего статистического ряда, а достаточно знания только двух его числовых характеристик» [11].

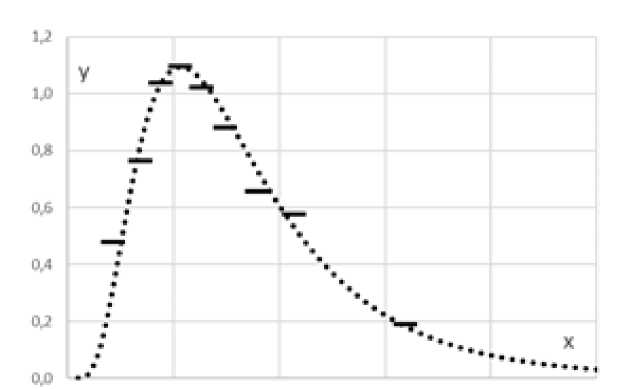
На рис. 1 пунктирная линия - график функции плотности распределения по заработной плате работников организаций г. Москвы, параметры которой определены на основе кусочно-линейной интерполяции твблично заданной функции распределения [13]. Здесь, как и на других рисунках статьи, на оси абсцисс откладываются приведенные уровни заработной платы. Последние вычисляются как отношение заработной платы к среднему его значению, выраженное в процентах. В рассматриваемом случае соответствующая эмпирическая функция плотности является кусочно-постоянной (она изображена условно на рис. 1 горизонтальными штрихами). Как видим, график теоретической функции плотности (2) достаточно хорошо аппроксимирует эмпирическую функцию.

g So к» tio tig tig

Рис. 1. Эмпирическая и теоретическая (логнормальная) функции плотности распределения работников организаций г.Москвы по заработной плате в апреле 2019 г.

Источник: расчеты авторов по данным Росстата [13]

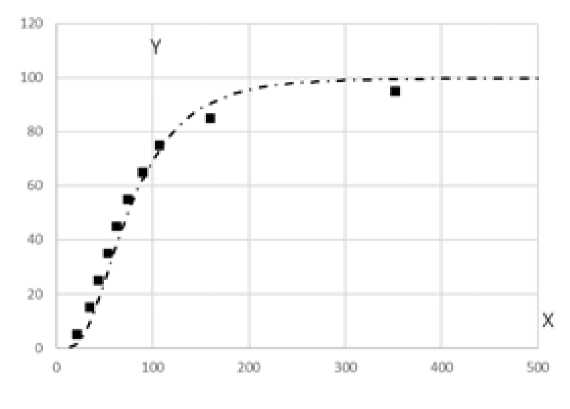
Рис. 2. Эмпирическая и логнормальная функции распределения работников организаций г.Москвы по заработной плате в апреле 2019 г.

Источник: расчеты авторов по данным Росстата [13]

Прямоугольники на рис. 2 - точки А_к ( x_k , у_к ) , где у_к = 10 к — 5 , x_k = 100 ц / Ц , Ц — средний доход в к -ой децильной группе работников, Ц — средний доход всех работников организаций г. Москвы, к = 1,2,...10. Здесь же на рис. 2 приведен график функции распределения по заработной плате работников организаций г. Москвы (штрих-пунктирная линия), которая соответствует функции плотности распределения, изображенной на рис. 1. Как видим, график логнормальной функции распределения (1) достаточно хорошо аппроксимирует эмпирическую функцию распределения при значениях заработной платы, которую получает 80% работников. Однако, для 20% работников с наибольшими заработками график логнормального распределения, соответствующего функции плотности распределения, изображенной на рис. 1, проходит существенно выше эмпирических точек А_к ( x_k ,у_к ) , где к = 1,2,...10. Поэтому функция плотности, график которой приведен на рис. 1, не адекватно отражает реальное распределение работников организаций г. Москвы по заработной плате.

2.    Применение параболического сплайна

Для повышения точности аппроксимации функции распределения у = F ( x ) мы использовали квадратичный сплайн; в этом случае соответствующая эмпирическая функция плотности является кусочно-линейной [13, 14]. Приведем основные формулы для следующего случая: з адана таблица ( x_k ; у_к ), где к = 0,1,..., n , n + 1. Здесь у ₀ = 0, y n _{+ 1} = 1, x_{k —} 1 <  x_k , у_{к —} 1 <  у_к , где к = 1,..., n , n + 1.

• 3.1.    Функция распределения раселения по доходу:

0, если x < x ₀;

F ^{( x} ) = 1 У к — 1 ^{+ а} к ^{( x — х} к — 1 ) ^{+ Ь} к ^{( x — х} к — 1 ⁾²

если x е [ x_k__р x _k ), к = 1,

n + 1;

• 1,    если x >  x ,. ,                      n + 1

• 3.2.    Функция плотности распределения: f ( x ) = F ( x ) .

• 3.3.    Функция, обратная функции распределения: x = ф (y ) , ф (y ) = F 1 ( y ) , у е [0,1]. Если У е [ Ук - 1 , Ук ], к = 1,..., n + 1, то

Здесь a_k >  0 , к = 1,..., n , n + 1.

0, если x <  x ₀;

f ( x ) = 1 a_k + 2Ь_к ( x - x_{k ч}), к = 1,..., n + 1;

0, если x >  x_{n +1}.

d k = У к ^- У к - i    h k = x k ^- x k - i

x ₀, если у = 0;

ф ⁽ У ) =

< xk - 1 ^xk - 1

+ ( У - Ук - 1 ) / a k , если Ь_к = 0;

+ ( 4D - a k )/(2 b k ), если Ь_к ^ 0;

_ x n + 1 , если у = 1.

• 3.4.    Средний доход: Д = J ф (y ) dy . Интегрируя функцию (6), получаем: о

n + 1 д = Е r k , к = 1

где при к = ^1,...^{, n} + ¹ имеем: r_k = cklL , ^d k = У_к ^- У к - 1

x k - 1

/  2               X3/2

а_к ( a k ^{+ 4} b k d k )   - a.

Д к = 1

2 Ь к

12 Ьк dk

3 3

—, если Ь_к * 0;

x ^{k 1} + x ^k , если b = 0.

• 3.5.    Вычисление параметров сплайна. Отметим, что функции (4) и (5) должна быть непрерывны. Поэтому справедливы равенства

У к = У к - 1 ⁺ a k ⁽ x k ^- x k - 1 ) ^{+ Ь} к ⁽ xk ^- xk - 1 ^{) 2} , a k + 1 = a k ^{+ 2 Ь} к ⁽ xk ^- xk - 1 ) •

Обозначим h_k = x_k - x_k__p u_k = d_k / h_k , где к = 1,..., n + 1. Тогда из условий непрерывности функций (4) и (5) получаем: u ^ = a_k + Ь^_к, a_{k+ 1} = a_k + 2 Ь^_к . Известно, что интерполяционный параболический сплайн имеет один свободный параметр [14]. Будем считать, что значение параметра a известно. Тогда полученные соотношения позволяют вычислить все остальные значения параметров сплайна:

^Ь 1 = ^{( и}1 - ^a 1 ) / h 1 , a k + 1 = ^{2 Ь}k^hk ⁺ a k , ^Ь к + 1 = ⁽ uk + 1 - a k + 1 ) / h k + 1 , где к = 1,..., n .

Таким образом, сплайн и все соответствующие функции зависят от параметра a . Средний доход также является функцией параметра a_v : Д = д ( a ).

Выбор значения свободного параметра a зависит от имеющейся информации. Если средний доход известен, то значение параметра ах находим из решения уравнения Ц = ц(а1). Если средний доход не известен, то значения параметра a находим из условия минимизации интегральной гладко- n+1

W(a ) = ^ bk 2 , при выполнении к=1

сти функции распределения, которая вычисляется по формуле условия ак > 0, где к = 1,...,П +1.

На рис. 3 приведен график интерполяционного параболического сплайна (линия 1), который отражает распределение по заработной плате работников организаций г. Москвы (пунктирная линия). Узлами сплайна служат те же точки А_к ( x_k , у_к ) , где к = 1,2,...10, что и точки на рис. 2. Штрих-пунктирная линия 2 на рис. 3 – график логнормальной функции распределения по заработной плате работников организаций г. Москвы, параметры которой определены в результате минимизации функции (3).

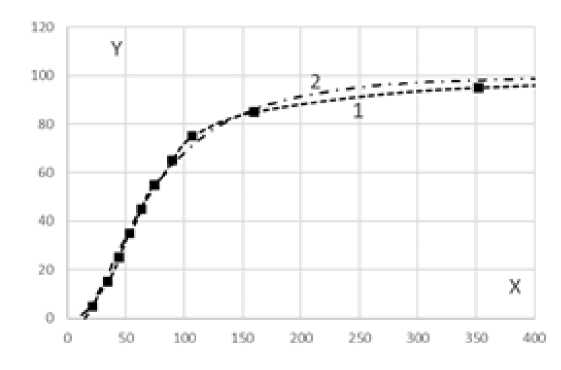
Рис. 3. Аппроксимация распределения работников организаций г.Москвы по заработной плате в апреле 2019 г. параболическим сплайном (линия 1) и логнормальной функцией (линия 2).

Источник: расчеты авторов по данным Росстата [13]

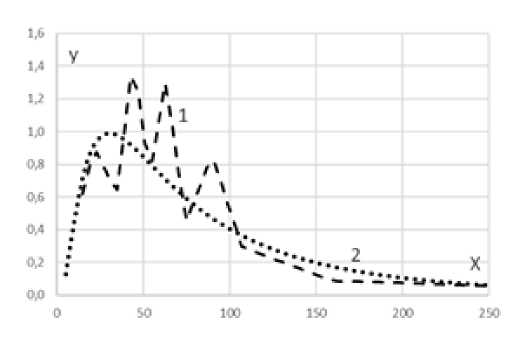
Рис. 4. Графики функций плотности распределения работников организаций г.Москвы по заработной плате в апреле 2019 г. (линия 1 – линейный сплайн, линия 2 – логнормальная функция).

Источник: расчеты авторов по данным Росстата [13]

Как видим, график логнормальной функции распределения (1) достаточно хорошо аппроксимирует эмпирическую функцию распределения при значениях заработной платы, которую получает около 85% работников. Однако, для 15% работников с наибольшими заработками график логнор- мального распределения на рис. 3 проходит выше интерполяционного параболического сплайна (линия 1). Если принять (на основании рис. 3), что сплайн более адекватно отражает распределение работников по заработной плате, чем логнормальное распределение, то использование посдеднего в рассматриваемом случае приведет к занижению среднего значения заработной платы и искажению показателей дифференциации (коэффициента Джини и др.).

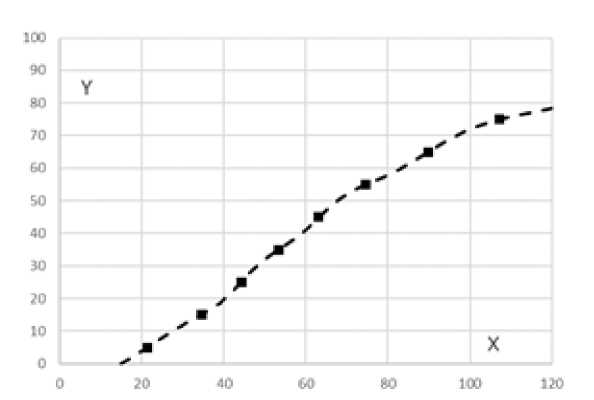
Рис. 5. Гафик сплайновой функции распределения работников организаций г.Москвы по заработной плате при значениях заработной платы ниже 120% от ее среднего значения.

Источник: расчеты авторов по данным Росстата [13]

Отметим еще одну особенность рассматриваемых статистических данных, которая иллюстрируется на рис. 4. На этом рисунке приведены графики функций плотности распределения работников организаций г.Москвы по заработной плате в апреле 2019 г., соответствующие функциям распределения, графики которых приведены на рис. 3. Здесь линия 1 – линейный сплайн, линия 2 – логнормальная функция плотности распределения. Как видим, график сплайновой функции плотности (линия 1) имеет несколько локальных максимумов и, следовательно, сплайновая функция распределения работников организаций г.Москвы по заработной плате в апреле 2019 г. (линия 1 на рис. 3) имеет несколько точек перегиба. Это хорошо видно на рис. 5, где приведен начальный участок сплайновой функции распределения при значениях заработной платы ниже 120% от ее среднего значения. В заключение обратим внимание на то, что, согласно рис. 3 и рис. 5, заработная плата более 70% работников организаций г. Москвы не тпревышает значения средней заработной платы всех работников.

Выводы

Использование сплайновой функции распределения достаточно адекватно отражает распределение населения по доходам. Выполненные расчеты с использованием сплайновой модели дают основание сделать вывод о том, что логнормальное распределение не является универсальным законом распределения. Показано, что особенностью функции распределения работников всех организаций г. Москвы в апреле 2019 г. по заработной плате является наличие у нее нескольких точек перегиба, в результате чего соответствующая функция плотности имеет несколько локальных максимумов. Для повышения адекватности модели распределения населения по доходам предполагается в дальнейшем модифицировать использованный здесь подход, представив «хвост» распределения экспоненциальной функцией у = 1 - (1 - y n ) exp[( x n - x ) / h ], где x >  x_n .