Применение правила Баркера к неорганическим стеклам

Баркер [1] для 68 различных твердых тел (в основном для металлов и аморфных полимеров) установил, что произведение модуля упругости при одноосной деформации E на квадрат коэффициента теплового линейного расширения (КТР) α ² есть величина постоянная

α ²E = 150(дин∙см^-2∙К^-2).                                               (1)

Данное сообщение посвящено применению этого правила к двухкомпонентным силикатным, германатным, боратным, фосфатным и халькогенидным стеклам. Необходимые экспериментальные данные взяты из базы данных SciGlass [2] и справочника [3].

Результаты обработки экспериментальных данных

У большинства исследованных нами стеклообразных систем данное правило выполняется вполне удовлетворительно. Например, у бескислородных халькогенидных стекол P–Se в достаточно широком интервале содержания P (от 2 до 21 мол. %) указанное произведение постоянно (табл. 1) α ²E = 150(дин∙см^-2∙К^-2), и между Е и 1/ α ² наблюдается линейная корреляция (рис. 1). Вместе с тем у ряда стекол произведение α ²E постоянно, однако численное значение существенно отличается от правила Баркера (1), в частности, у свинцовоборатных стекол (табл. 1, рис. 2).

Обсуждение полученных результатов

Особенность правила Баркера заключается в том, что равенство (1) однозначно связывает линейную (гармо- ническую) E и нелинейную (ангармоническую) а величины. Встречаются другие подобные корреляции [4-9], например, соотношение Беломестных – Теслевой [7], выражающее связь параметра Грюнайзена γ с функцией коэффициента Пуассона μ,

3 Г 1 + ц "1

Таблица 1

2 I 2 — 3 Ц J , где μ – гармоническая, γ – ангармоническая величины.

Коэффициент теплового линейного расширения α и модуль упругости при одноосной деформации E для ряда стекол

№	Состав стекла, мол.%		E∙10-9, дин∙см	α∙107, К -1	α2E, дин∙см-2∙К-2
1	P 2.02	Se 97.98	101	400	162
2	4.18	95.82	104	392	161
3	8.93	91.07	120	370	164
4	8.93	91.07	116	375	164
5	13.58	86.42	115	370	158
6	20.73	79.27	113	383	166
7	PbO 12.8	B 2 O 3 87.2	311	94	28
8	15.2	84.8	364	83	25
9	16.2	83.8	407	79	25
10	17.7	82.3	449	74	24
11	18.5	81.5	497	71	25

Вместе с тем в настоящее время природа этого явления остается во многом неясной. Часто встречается представление о том, что гармонические и ангармонические характеристики являются независимыми друг от друга свойствами твердых тел. Представляет интерес работа [4], где на основе приближенного подхода сделана попытка качественно объяснить данный факт.

В рамках одномерной модели твердого тела потенциальная энергия межатомного взаимодействия двух смежных частиц записывается в виде

23 ax x

U =,                                                 (1)

где а = (d²U/dr²)_r =ro - гармонический, b = -(1/2)(d³U/dr³) _r = _ro - ангармонический коэффициенты в разложении U(x) в ряд по смещениям частиц из равновесного положения x = (r-r o ).

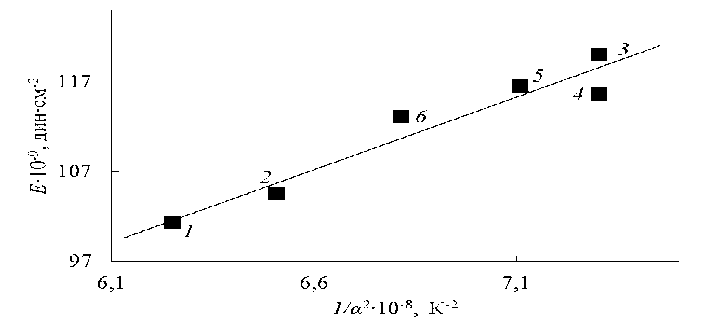
Рис. 1. Линейная корреляция между модулем упругости E и обратной величиной квадрата коэффициента теплового расширения α стекол P–Se. Номера точек соответствуют номерам стекол в таблице

Б.С. Сыдыков, А.А. Машанов, Д.С. Сандитов. Применение правила Баркера к неорганическим стеклам

Используя в указанных производных уравнение Ми

U = -Ar-m + Br-n

Конторова [4] получает следующую связь между гармоническим и ангармоническим коэффициентами:

,     । m + n + 3 ।

b = I                     I a .

V ² r 0       )

Она установила функциональную зависимость коэффициента теплового расширения и модуля упругости (и других подобных свойств) от этих коэффициентов a и b. Отсюда объясняет обсуждаемое явление наличием связи между a и b типа (4) и зависимостью от них линейных и нелинейных свойств твердых тел.

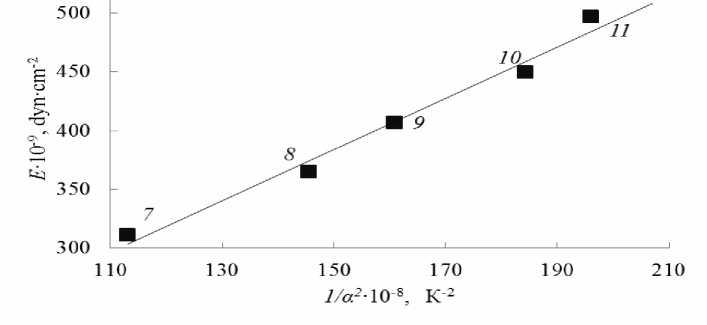
Рис. 2. Линейная корреляция между модулем упругости E и обратной величиной квадрата коэффициента теплового расширения а стекол PbO-B2O3. Номера точек соответствуют номерам стекол в таблице 1

Таким образом, подход Конторовой указывает на принципиальную возможность реализации корреляций между, казалось бы, совершенно различными по своей природе физическими свойствами твердых тел, в том числе гармоническими и ангармоническими величинами. Причиной существования этих связей является общность закона взаимодействия между частицами для данной группы твердых тел [4]. Полный ответ на данный вопрос можно получить только при условии знания функции U(x) и наличия микроскопических теорий гармонических и ангармонических свойств. К сожалению, в настоящее время нет таких общепризнанных микроскопических теорий и строго установленной функции U(x).

Элементарная молекулярная теория теплового расширения твердых тел по Френкелю [5] приводит к выводу о том, что у твердых тел, у которых молярные объемы близки V ≈ const, произведение КТР на модуль упругости есть величина постоянная [10]

аЕ « —— ® const , (5)

2V где R – универсальная газовая постоянная.

Баркер [1] показал, что у однородных изотропных твердых тел разность теплоемкостей Cp – CV= 9α2BTVT с привлечением формулы теории упругости

B

T

E

3(1 - 2 Ц )

может быть выражена через произведение α2E. Он приходит к заключению, что постоянство произведения α2E

означает постоянство отношения (C p – C V /V). Из правила Баркера, устанавливающего взаимосвязь между гармонической и ангармонической величинами, следует, что глубина потенциальной ямы влияет на форму кривой потенциала U(x) [1].

Заключение

У двухкомпонентных неорганических стекол разных классов при определенных изменениях содержания компонентов произведение квадрата коэффициента линейного теплового расширения на модуль упругости остается постоянной величиной: α2E ≈ const. В соответствии с этим правилом между E и 1/α2 наблюдается линейная корреляция. Причиной существования определенной связи между гармоническими и ангармоническими величинами является общность закона взаимодействия между атомами (молекулами) для данного класса стекол.