Применение расчетно-экспериментального метода анализа сложнонапряженного состояния резиновых мембран для эффективных решений их производства

Резиновые мембраны нашли широкое применение в различных отраслях промышленности и в настоящее время область их использования постоянно расширяется. На практике существуют тысячи рецептур резиновых мембран, нередко на основе дорогостоящих каучуков, что связано с разнообразными условиями их эксплуатации и спектром предъявляемых к ним требований [1].

Конкурентоспособность создаваемого изделия, в том числе мембран, определяется совокупностью факторов [2-5]:

─ качеством, в том числе требуемыми техническими характеристиками;

─ стоимостью, в том числе возможностью производства из доступных материалов;

─ сроками, в том числе временем от момента начала проектирования до поступления готовой продукции заказчику.

Существующий процесс создания резиновых мембран является ресурсоемким, т. к. требует проведения большого массива экспериментальных исследований. Кроме того, стандартные лабораторные испытания, которые используются при разработке рецептуры резин, не отражают неоднородное сложнонапряженное состояние, характерное для реальных условий эксплуатации мембран [6].

Поскольку производство новых изделий с заданными характеристиками в современных реалиях происходит в условиях дефицита времени, а также материальных и финансовых ресурсов, то в соответствии с ГОСТ Р 54869–2011, PMBOK и РRINСЕ2 [7-8] процесс создания резиновых мембран, являющийся инженерным творчеством, можно рассматривать как проектное решение, т. е. комплекс взаимосвязанных мероприятий, направленный на создание уникального продукта или услуги в условиях временных и ресурсных ограничений.

Для реализации проектных решений, обеспечивающих конкурентоспособность резиновых мембран, был разработан новый подход к процессу их создания, включающий как проведение простых лабораторных испытаний, позволяющих моделировать поведение мембран в условиях эксплуатации, так и анализ напряженно-деформированного состояния (НДС) с применением корректных физических моделей, максимально учитывающих характеристики резин и их изменение в процессе эксплуатации [9].

Методы исследований

Для создания резиновых мембран необходимо обоснованно подойти к выбору методов их испытания. К методам испытаний предъявляются следующие требования:

─ условия испытания образца должны отражать реальные условия нагружения изделия и обеспечивать высокую точность и достоверность результатов;

─ на одном типе образца можно определить не только деформационные, но и предельные характеристики материала;

─ испытания можно проводить на существующем стандартном оборудовании с применением недорогих адаптированных приставок.

Данным требованиям полностью удовлетворяет метод продавливания резиновой мембраны стальным шарообразным индентором [10]. Авторы метода изучали механизм разрушения протекторных резин при движении по гравийной дороге, поэтому использовали сферический индентор малого диаметра, а также цилиндрический индентор и индентор в виде призмы с целью реализации разрушения образца в виде прокола. В настоящей работе требовалось оценить физикомеханические характеристики резин для мембран, а также их напряженно-деформированное состояние, поэтому методы по оценке прочности и сопротивления раздиру были соответствующим образом адаптированы, в частности увеличен диаметр индентора [9]. Индентор цилиндрической формы и в форме призмы были исключены из дальнейших исследований.

Предлагаемые методики испытания резин в неоднородном сложнонапряженном состоянии просты в аппаратурном исполнении (рисунок 1) и обеспечивают высокую воспроизводимость результатов.

Рисунок 1. Нагружение резиновой мембраны шарообразным индентором

Figure 1. Loading of rubber membrane with a spherical indenter

При продавливании мембраны индентором возникает неоднородное сложнонапряженное состояние, поэтому определить значения прочностных показателей на основании только экспериментальных данных невозможно. Решить данную проблему можно путем численного моделирования [11-14] процесса нагружения резиновой мембраны сферическим индентором.

На основании анализа напряженно-деформированного состояния резиновых мембран (рисунок 2), реализующегося при нагружении их шарообразным индентором, сформулирован критерий для прогнозирования прочности и выбрано уравнение состояния материала, адекватно отражающее его механические свойства (1).

F (S, S2 ) = aSx +(1- a) S2 = C,      (1)

где S 1 и S 2 – первый и второй инварианты тензора напряжений; a и C – экспериментально определяемые коэффициенты: C = f p a - характеризует прочность материала, МПа; f – условная прочность при одноосном растяжении, МПа; a = S ₂ Д f + S ₂ - S j ) - характеризует относительный вклад первого инварианта (нормальных напряжений) в прочность, соответственно, (1- а ) характеризует стойкость к напряжениям, связанным с изменением формы.

Комплексное использование теоретического и экспериментального подходов является необходимым ресурсом для решения задачи создания резиновых мембран с заданными характеристиками.

Результаты

Данный подход рассмотрен на примере создания цельнорезиновой гофрированной мембраны автоматического клапана продувки рукавных фильтров.

Ресурс имеющихся мембран не отвечал требованиям потребителя.

Особенности работы изделия:

• •    мембрана подвергается статическим деформациям ~ 20 ÷ 30%;

• •    в пневмолиниях, где эксплуатируется мембрана, возможно наличие паров масла;

• •    в процессе эксплуатации материал рабочей части мембраны испытывает разносторонне направленные напряжения;

• •    на рабочей поверхности мембраны имеется перепускное отверстие, предназначенное для предотвращения срабатывания пневматического устройства при небольших, «шумовых», значениях перепада давления воздуха по разные стороны мембраны.

С точки зрения распределения напряжений в рабочей части изделия при его эксплуатации, перепускное отверстие является конструктивно обусловленным дефектом и, следовательно, концентратором напряжений. Именно на поверхности этого отверстия в процессе работы возникали трещины, обуславливающие выход мембраны из строя. Таким образом, изделие работает в условиях неоднородного сложнонапряженного состояния и искусственного концентратора напряжений.

При разработке рецептуры резиновых смесей для производства мембран рассматриваемого типа с повышенным ресурсом работы, в первую очередь следует добиваться максимально возможного значения сопротивления раздиру резин в условиях неоднородного сложнонапряженного состояния (естественно, сохраняя в заданных пределах значения других необходимых свойств).

Испытание резин на основе широко использующихся в промышленности РТИ [15] каучуков: СКИ-3, СКМС-30АРК, БНКС-18АМН, БНКС-28АМН и БНКС-40АМН предложенными методами показало, что лучшим сопротивлением раздиру обладают резины на основе бутадиен-нитрильных каучуков, наполненных техническим углеродом N339 (рисунок 2). Как известно эти же каучуки обеспечивают изделиям высокую маслостойкостью, что важно для данной гофрированной мембраны.

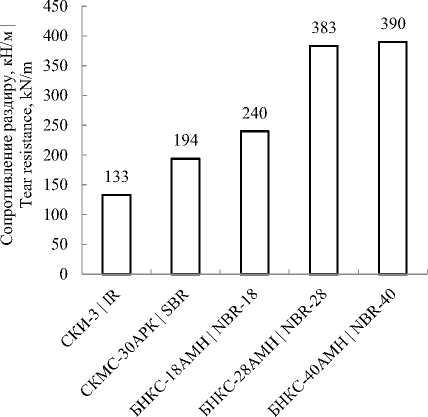
Рисунок 2. Сопротивление раздиру резин в неоднородном сложнонапряженном состоянии

Figure 2. Tear resistance of rubbers in a heterogeneous complexly stressed state

Дальнейшие исследования проводили на бутадиен-нитрильных каучуках [16]. Содержание активного наполнителя – технического углерода N339 варьировалось от 30 до 50 мас. ч. на 100 мас. ч. каучука.

Вулканизаты были испытаны по методике оценки сопротивления раздиру в неоднородном сложнонапряженном состоянии. Для оценки стойкости к воздействию масел дополнительно для всех резин были проведены серии экспериментов по определению прочностных характеристик после выдержки в течение одного месяца в индустриальном масле И-40А, широко использующемся в промышленности, например, в качестве сказки для редукторов.

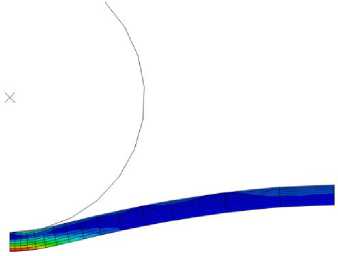
Прочностные характеристики резин оценивали по величине коэффициента «С», который определялся посредством расчета методом конечных элементов [17-19] по формуле (1). Задачу о продавливании резиновой мембраны сферическим индентором решали в осесимметричной постановке (рисунок 3). Для задания свойств резин при расчете методом конечных элементов использовался упругий потенциал Йоха, хорошо учитывающий нелинейность изменения свойств резин при нагружении [20–23]. Расчет показал, что при небольших деформациях область концентрации напряжений сосредоточена на оси симметрии модели в центре под областью контакта образца и индентора (рисунок 3, б). При дальнейшем деформировании происходит резкое перераспределение напряжений, и при больших перемещениях индентора область концентрации напряжений в центре образца сглаживается (рисунок 3, в), а концентрация напряжений на периферии, наоборот возрастает и становится наиболее опасной зоной сечения. Характер разрушения образцов подтверждает корректность проведенного расчета. В таблице 1 приведена оценка прочностных характеристик резин до и после набухания в масле. При испытании резин, не подвергнутых воздействию масла значения коэффициента «С» повышаются в ряду каучуков: БНКС-18АМН → БНКС-28АМН → БНКС-40АМН, что свидетельствует о росте прочности резин с увеличением содержания нитрила акриловой кислоты в молекуле рассматриваемых каучуков. Увеличение прочности наблюдается и при увеличении дозировки технического углерода. После выдержки в масле прочность несколько снижается для всех резин на основе каучука БНКС-18АМН и практически не изменяется для резин на основе каучуков БНКС-28АМН и БНКС-40АМН.

(a)

(b)

Рисунок 3. Характер разрушения мембран (a) и распределение эквивалентных напряжений Мизеса (b), (c) на различных стадиях внедрения индентора

Figure 3. The nature of membranes destruction (a) and the distribution of equivalent von Mises stresses (b), (c) at different stages of the indenter penetration

(c)

Таблица 1.

Влияние выдержки в индустриальном масле на прочностные свойства анализируемых резин

Table 1.

An influence of aging in industrial oil on the strength properties of the analyzed rubbers

Коэффициент "С" при перемещении (мм), МРа Coefficient "С" at moving (mm), МРа	Тип каучука | Type of rubber
	БНКС-18АМН | NBR-18			БНКС-28АМН | NBR-28			БНКС-40АМН | NBR-40
	Дозировка технического углерода N339, мас. ч. | Dosage of carbon black N339, parts by weight
	30	40	50	30	40	50	30	40	50
До выдержки в масле И-40А | Before aging in oil I-40А
10	2.2	2.5	2.9	4.0	4.5	5.0	4.9	5.1	5.3
20	4.0	4.5	4.8	8.0	8.7	10.0	9.8	10.2	10.4
30	10.5	10.8	11.3	14.1	15.5	16.9	16.8	17.1	17.3
При разрыве At break	16.2	16.8	17.0	19.5	21.1	22.9	22.4	23.2	23.5
После выдержки в масле И-40А | After aging in oil I-40А
10	1.1	1.5	1.9	3.7	4.4	4.9	4.8	5.0	5.2
20	3.1	3.6	4.0	7.8	8.6	9.8	9.7	10.1	10.3
30	9.7	10.0	10.5	13.9	15.4	16.8	16.7	16.9	17.2
При разрыве At break	14.2	15.8	16.1	19.3	20.9	22.5	22.2	23.1	23.5

Зависимость сопротивления раздиру от типа каучука и содержания наполнителя качественно аналогична зависимости прочности (таблица 2). При этом стоит отметить, что у резины на основе БНКС-18АМН после выдержки в масле наблюдается достаточно значимое (10 ÷ 25%) снижение сопротивления раздиру. У резин на основе каучуков БНКС-28АМН и БНКС-40АМН снижение сопротивления раздиру незначительно.

Таблица 2.

Влияние выдержки в индустриальном масле И-40А на сопротивление резин раздиру

Table 2.

An influence of aging in industrial oil I-40А on the tear resistance of rubbers

Показатель Indicator	Тип каучука | Type of rubber БНКС-18АМН | NBR-18     БНКС-28АМН | NBR-28     БНКС-40АМН | NBR-40 Дозировка технического углерода N339, мас. ч. | Dosage of carbon black N339, parts by weight 30       40       50       30       40       50       30       40       50
Сопротивление раздиру T s , кН/м Tear resistance, kN/m	До выдержки в масле И-40А | Before aging in oil I-40А 210     302     311      256     383      392“И  268 “И  391      401 После выдержки в масле И-40А | After aging in oil I-40А 192      267      274      251      380      391      267      390      401

На основании совокупности данных по оценке прочности и сопротивления раздиру, для производства гофрированных мембран могут быть рекомендованы резины как на основе каучука БНКС-28АМН, так и на основе БНКС-40АМН с содержанием техуглерода в количестве 40 и 50 мас. ч. на 100 мас. ч. каучука, поскольку они обладают сопоставимыми свойствами. Однако резины на основе каучука БНКС-40АМН с содержанием технического углерода 40 и 50 мас. ч., а также резины на основе БНКС-28АМН с содержанием технического углерода 50 мас. ч. имеют повышенные жесткостные характеристики, о чем свидетельствуют значения коэффициента «С» при небольших значениях перемещения индентора (таблица 1). Это негативно сказывается на работе данной гофрированной мембраны. Таким образом, можно считать, что оптимальный комплекс характеристик будут обеспечивать резины на основе каучука БНКС-28АМН при наполнении техуглеродом N339 в количестве 40 мас. ч. на 100 мас. ч. каучука.

Использование комплексного расчетно-эк-периментального подхода позволило повысить долговечность изделий, испытанных в лабораторных условиях, на 35% по сравнению с эталоном и сократить сроки их создания. При этом в рецептуре использован доступный бутадиен-нитрильный каучук, что особенно важно в современной экономической ситуации.

Заключение

Таким образом, испытания резин методом продавливания, моделирующим неоднородное сложнонапряженное состояние, имеющее место в реальных условиях эксплуатации изделий, позволяет получить широкий спектр достоверных характеристик резин для мембран. Применение метода конечных элементов упрощает идентификацию НДС резиновых мембран и при этом является необходимым ресурсом создания РТИ, который может быть эффективно использован в сочетании с широким спектром методов лабораторных испытаний. Сочетание экспериментального и теоретического подходов позволяет адекватно воспроизводить НДС мембран, добиться существенного сокращения времени, материальных и финансовых затрат на создание резиновых мембран с заданными техническими характеристиками.