Применение сегментного анализа для разработки стратегии развития образовательного учреждения

Особенность задач управления часто состоит в том, что решение должно быть обязательно принято независимо от того, в состоянии ли мы точно оценить результаты, к которым приведет принятое решение. Типичным для задач управления является случай, когда имеющаяся информация бывает или недостаточна для точной оценки ситуации, или искажена посторонними факторами, тем не менее, это обстоятельство не снимает необходимости принятия решения [1]. Таким образом, в процессе управления возникает важная задача принятия решения в условиях, когда информация о сложившейся ситуации или недостаточна, или искажена [2]. Такого рода задачи получили название задач принятия решения в условиях неопределенности.

Одним из наиболее эффективных методов, позволяющих решать такие задачи является метод стохастического (динамического) программирования.

Пусть образовательное учреждение (ОУ) выпускает бакалавров и магистров экономического профиля. Оно может находиться в двух состояниях:

• 1    спрос на выпускников есть;

• 2    спроса на выпускников нет.

Работой организационных структур по набору наиболее подготовленных абитуриентов, влияющих на качество подготовленных специалистов, можно управлять с помощью двух стратегий:

• с тратегия 1 — работать с окружающей средой, например, усилить рекламу среди выпускников ориентированных на классический университет, как наиболее подготовленных;

стратегия 2 — дифференцировать предложения на основе субсегментации потребителей путем открытия новых специальностей, ориентированных на новые, например, биотехнологические направления.

Для каждой стратегии задана своя стохастическая матрица (матрица вероятностей перехода из одного состояния в другое) и своя матрица востребованности выпускников. Здесь Р1, Р2 — матрицы вероятностей переходов образовательного учреждения из одного состояния в другое. Например, Р1 11 — вероятность того, что ОУ, находящееся в состоянии 1 останется в этом состоянии, Р1 12 — вероятность того, что ОУ, находящееся в состоянии 1 перейдет в состояние 2, Р1 22 — вероятность того, что ОУ, находящееся в состоянии 2 останется в этом состоянии и Р1 21 - вероятность того, что ОУ, находящееся в состоянии 2 , перейдет в сосотяние1. Таковы же элементы матрицы Р2.

В матрице R1 элемент R1 11 — ожидаемый процент прироста трудоустроившихся выпускников, если он останется в состоянии1, R1 12 — ожидаемый процент прироста трудоустроившихся выпускников при переходе из состояния 1 в состояние 2, R1 22 - ожидаемый процент прироста трудоустроившихся выпускников (отрицательное число, т.к. процент прироста трудоустроившихся выпускников уменьшается), остающегося в состоянии 2, R1 21 ожидаемый процент прироста трудоустроившихся выпускников при переходе из состояния 2 в состояние 1. Таков же смысл элементов матрицы R2.

Решение проблемы разработки стратегии развития образовательного учреждения состоит в том, чтобы, в каком бы состоянии ОУ не находилось, выбрать стратегию (управление), которая приносит максимальный ожидаемый процент прироста трудоустроившихся выпускников [3].

Поставленная проблема сводится к стохастической задаче: управление (выбор стратегии) изменяет вероятность перехода из одного состояния в другое. Переход происходит дискретно, т.е. это дискретный случайный процесс. При выборе стратегии вероятность перехода из одного состояния в другое зависит только от состояния в настоящий момент времени [4]. Следовательно, этот случайный процесс является Марковским. Ожидаемый процент прироста трудоустроившихся выпускников — это сумма вероятностей получения того или иного дохода.

Рассмотрим отдельные шаги прогнозирования стратегии. Для первого шага выбора стратегии обозначим через F ожидаемый процент прироста трудоустроившихся выпускников. Если ОУ находится в состоянии 1, то оно может остаться в этом состоянии или перейти в состояние 2. При этом может быть использована как стратегия 1, так и стратегия 2. В первом случае F 11 - ожидаемый процент прироста трудоустроившихся выпускников при состоянии 1 и выборе стратегии 1 составляет: F 11⁼ Р1 11 R1 11 +Р1 12 R1 12 . После подстановки чисел получим. F 11 = 6.

Аналогично, при выборе стратегии 2 ожидаемый процент прироста трудоустроившихся выпускников будет составлять F 12 = Р2 11 R2 11 +Р2 12 R 12 =4.

Однако ОУ может находиться в состоянии 2 и для управления также может быть выбрана одна из стратегий. В этом случае: F 21 =P1 22 R1 22 +P1 21 R1 21 =-3 при выборе первой стратегии и F 22 =Р2 22 R2 22 +P2 21 R2 21 =-5 при выборе второй стратегии.

Эти расчеты можно сделать выбором на первом шаге управления. Для получения максимального ожидаемого процент прироста трудоустроившихся выпускников следует выбрать стратегию 1 (работать с окружающей средой, например, усилить рекламу среди выпускников ориентированных на классический университет, как наиболее подготовленных), в каком бы состоянии ОУ не находилось.

На каждом следующем шаге «n» управления мы должны выбирать управление так, чтобы получить максимальный ожидаемый процент прироста трудоустроившихся выпускников за все «n» шагов. Обозначим максимальный ожидаемый процент прироста трудоустроившихся выпускников за первый шаг при нахождении завода в состоянии 1 через f1, а при нахождении

ОУ в состоянии 2 через f2. Из предыдущих расчетов следует, что f1=6 и f2=-3.

На втором шаге управления ожидаемый процент прироста трудоустроившихся выпускников с учетом максимального ожидаемого процента прироста трудоустроившихся выпускников на первом шаге составит при нахождении ОУ в состоянии 1 и выборе стратегии 1:

F 11 = Р1 22 (R1 22 + f1) + Р1 12 (R1 12 +f2) = 0,5(9+6) + 0,5 (3-3) =7,5 или

F 12 =Р2 11 (R2 11 +f1)

+Р2 12 (R2 12 +f2)=0,8(4+6) +0,2( 4-3)=8,2 при выборе стратегии 2.

Очевидно, что при нахождении ОУ в состоянии 1 следует для получения максимального ожидаемого процента прироста трудоустроившихся выпускников выбирать стратегию 2, т. к. f1 =8,2.

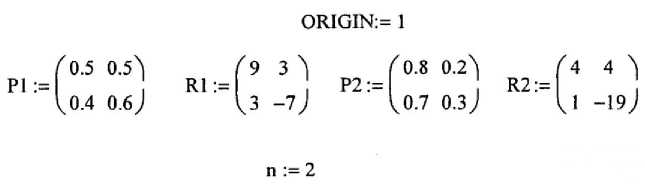
Рисунок 1. Начальные данные для расчета стратегических параметров развития

u :=

f ^

10 )

for i e 1 .. n

F1,1 ^ P'1,1(R11,1 + f1) + P'JRh,2 +

F1,2 ^ P21,1(R21,1 + f1) + P21,2(R21,2 +

F2,1 ^ P12, 2(R12,2 + f '' P12, 1(R12, 1 +

F2, 2 ^ P22, 2(R22,2 + f '' P22, 1(R22, 1 +

( u1 , i ^ 'Hmax , i ^ ^F1 , 1 ) l^fF1 , 1 >  ^F1 , 2 ^ ( и^ - ^ 2 ) v ( max^ i ^ Fl 2) ] otherwise ( ^u2 , i ^ ¹ )^v ( max , i ^ F2 , 1 ) if F2 , 1 >  F2 , 2 ^ ( u2 i ^ 2 ) v ( max j ^ F2 2) ] otherwise ^f1 ^ ^f1 + max , i ^f2 ^ ^f2 + ^ma2 , i

i

u =

u

Рисунок 2. Программа расчета прогнозных параметров на ЭВМ

При нахождении ОУ в состоянии 2, после аналогичных расчетов получим F 21⁼ P1 22 (R1 22 +f2) +Р1 21 (R1 21 +fl) =-2,4 при выборе первой стратегии и F 22 =P2 22 (R2 22 +f2) +Р2 21 (R2 21 +fl)= -1,7 при выборе второй стратегии.

Очевидно, что в обоих случаях для получения максимального ожидаемого процента прироста трудоустроившихся выпускников нужно выбирать стратегию 2.

Подобным образом рассчитывается стратегия развития ОУ (оптимальное управление) и на всех последующих шагах. Ниже представлена программа в Маткаде для решения данной задачи.

Запись ORIGIN=1 означает, что счет начинается не с нуля, а с единицы. Далее приводятся матрицы перехода и матрицы процентов прироста трудоустроившихся выпускников для двух стратегий (рисунок 1).