Применение схем высокого порядка аппроксимации при моделировании процессов торможения сверхзвуковых течений в прямоугольных каналах

Высокоскоростные потоки газов относятся к классу природных явлений, недостаточно изученных теоретическими методами. Практически вся информация о потоках, которой располагает человечество, получена, прежде всего, экспериментально [1]. В работе [2] именно экспериментальным путем исследуется одномодовый панельный флаттер в сверхзвуковом потоке газа. Теоретически одномодовый флаттер был рассмотрен лишь недавно. В [3] представлены результаты специальной оценки структуры течения для двух моделей криволинейных диффузорных каналов: с кольцевой и прямоугольной формами поперечного сечения. При стационарной постановке задачи обнаружено значительное различие между данными, полученными из натурных опытов, и результатами численных расчетов. В работах В.И. Лысенко с соавторами [4, 5] экспериментально анализируется устойчивость течения в области за плоской пластиной при сверхзвуковой скорости набегающего потока.

Несмотря на многолетние изыскания, процессы торможения сверхзвуковых течений в каналах все еще остаются «terra incognita» во многих аспектах газовой динамики [6]. Ранее такие процессы слабо проявлялись в работе двигательных установок и, соответственно, не считались важными для конструкторов. Кроме того, существующие теоретические методики не обеспечивали полного представления обо всех процессах, протекающих при сверхзвуковом течении. Особенно это касалось потоков вязкого газа.

Создание и эксплуатация нынешних поколений авиационной и ракетно-воздушной техники, работающей на высоких сверхзвуковых скоростях, требуют детальной информации о локальных газодинамических процессах, сопровождающих прохождение сверхзвуковых потоков по каналам. Новые поколения газодинамических устройств требуют точно определять границы устойчивой работы конструкции. Так, для управления процессами торможения необходимо иметь детальное представление о поведении и характеристиках высокоскоростных потоков в каналах [6]. В связи с этим встает вопрос о создании математической модели, базирующейся на современных численных методах, способной учитывать эти особенности.

Задача численного моделирования высокоскоростных течений газа даже при использовании современных вычислительных средств не является тривиальной. Для аккуратного расчета течений с воспроизведением реальных физических процессов требуется применение методов высокого порядка точности, минимизирующих численную вязкость до значений, меньших вязкости физической,

либо не обладающих численной диссипацией. Использование же схем низкого порядка приводит к тому, что картина течения, формирующаяся под действием численных эффектов, оказывается сглаженной и зачастую сильно отличающейся от настоящей. Таким образом, методы высокого порядка — это тот инструмент, который дает возможность рассчитывать высокоскоростные потоки вязкого газа при приемлемой для машинной памяти насыщенности сетки. В работе [1], например, приведена и протестирована методика расчета дозвуковых ламинарных, переходных и турбулентных потоков с высоким порядком точности. Показано, что докритический характер течений позволяет выполнять аппроксимацию пространственных производных с высоким порядком на основе центрально-разностных схем.

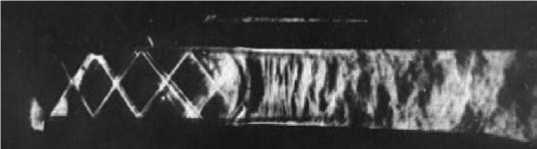
Рис. 1. Торможение сверхзвукового потока в канале при M = 2 (экспериментальная фотография [7])

В отличие от дозвуковых течений, закритические сверхзвуковые потоки характеризуются наличием крутых градиентов и разрывов параметров (экспериментальная фотография процесса торможения из работы [7] представлена на рисунке 1). Для предотвращения получения ложноосциллирующих решений конвективные слагаемые необходимо рассчитывать на адаптивных шаблонах с автоматическим анализом гладкости численных решений. Задачи данного исследования: на примере численного моделирования процесса торможения сверхзвукового потока продемонстрировать методику расчета с высоким порядком точности, базирующуюся на идеях WENO-метода и центрально-разностных аппроксимациях высокого порядка; для прямоугольного канала показать безвихревое безотрывное течение с лямбда-образной системой скачков и провести однопараметрическое теоретическое исследование (в зависимости от значения числа Маха) закритического течения вязкого газа на основе метода высокого порядка точности.

2.    Постановка задачи

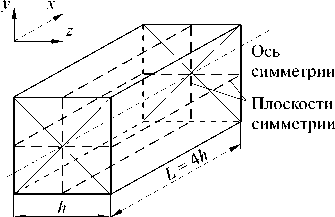
Рассматривается задача исследования сверхзвукового течения вязкого сжимаемого газа в прямоугольном канале с квадратным сечением. Расчетная область (см. Рис. 2) имеет ось симметрии и плоскость симметрии, на которых далее будут представлены распределения параметров. Решается следующая система уравнений, описывающих течение вязкого газа:

∂ρ+∇⋅ρU=0, ∂t

.

∂ρU+∇⋅ρUU+∇ P = 1(∆U+1∇∇⋅U),

∂ t              k M² Re 3

∂ρ ^E +∇⋅ρ E U +∇⋅ ^{P U} = ¹ ( ∇⋅ ( U ⋅ S ) - S : S ) +    ∆ ^T

∂ t              k M² Re                 ( k - 1)M²Pr

Здесь: ∇ — оператор набла (оператор Гамильтона); ∆ — оператор Лапласа; ρ — плотность газа; P — давление; E — удельная энергия; U — вектор скорости потока с компонентами

Рис. 2. Область интегрирования

(прямоугольный канал)                    U, V,   W ; S = (∂ui ∂xj +∂uj/∂xi -2δij∇⋅U / 3) / 2 — тензор вязких напряжений; k= CPCV — отношение теплоемкостей; M = U^c^ — число Маха; Re =ρ^U^hµ — число Рейнольдса; Pr =CPµλ — число Прандтля, а также c^= (kP^/ρ^)1/2 — скорость звука, λ , µ — коэффициенты теплопроводности и динамической вязкости,

C_P , C_V — изобарная и изохорная теплоемкости газа.

Уравнения (1)–(3) записаны в безразмерных переменных; покомпонентная запись уравнений приведена в работах [1, 8]. В качестве масштабов берутся: для линейных величин — высота (ширина) канала h, для скоростей — значение продольной компоненты вектора скорости потока на входе в канал U= U^ ; для давления и плотности — величины давления P^ и плотности ρ^ на входе в канал. Безразмерный масштаб для времени рассчитывается по формуле t^= hU^. Плотность ρ , компоненты вектора плотности тока ρU , ρV , ρW и энергия единицы объема ρE являются неизвестными, которые определяются в результате решения уравнений (1)–(3). Остальные газодинамические параметры выражаются через перечисленные выше пять переменных. Система замыкается уравнением состояния Менделеева– Клапейрона, которое не является следствием какого-либо закона сохранения и поэтому непосредственно в систему не включается, хотя в вычислениях участвует. Температура рассчитывается по формуле

T = k ( k - 1)M²

pE (p U )2 + (p V )2 + (p W )2' ---7----------------------------- p              2p            _ а безразмерное давление определяется как

P = k ( k - 1)M²

( p U )² + ( p V )² + ( p W )²' p E--

2p             .

В расчетах динамическая вязкость ц принималась постоянной, не зависящей от температуры (так как изменения температуры в решаемых примерах были малы) и равной 2 - 10 5 кг/м-с. Коэффициент теплопроводности принимался равным 0,03 Вт/(м∙К). Число Прандтля бралось равным 0,7, отношение теплоемкостей k — 1,4. В обезразмеренном виде ширина и высота канала равнялись единице, длина — четырем единицам. Область интегрирования покрывалась равномерной прямоугольной сеткой с общим числом узлов 50 400 800 (800×251×251).

Граничные условия были следующими:

• -    на входной границе значения параметров полагались равными значениям набегающего потока (p„ = 1, U_А= 1, V. = W. = 0, P. = 1);

• -    на выходной границе для всех параметров задавались «условия сноса» (дf /5n = 0, f = (p, P, U, V, W));

  – на твердых стенках канала выполнялись условия прилипания для скорости, кроме того, поверхность канала предполагалась адиабатической, то есть дT/5n = 0, где n — направление нормали (в простейшем случае дР/дn = 0 и dp/dn = 0 ).

3.    Метод решения уравнений

В качестве начальных условий во внутренних точках использовались параметры набегающего потока, на границах задавались приведенные выше краевые условия.

Расчеты проводились на суперкомпьютере «Уран» в ИММ УрО РАН (г. Екатеринбург). Процесс счета однонаправлено распараллеливался с помощью технологии MPI на 160 процессов. При этом коэффициент распараллеливания КР равнялся в среднем 0,81 ( КР = ( t_P 1 / t_{P 2} )/( P 2/ P 1 ) , где P 1, P 2 — количество процессоров, t_{P 1} , t_{P 2} — соответственное время счета на разном числе процессоров).

Для интегрирования уравнений (1)–(3) применялась следующая методика. Конвективные члены аппроксимировались с высоким порядком с помощью WENO-схем, для аппроксимации диффузионных членов использовался метод центральных разностей также с высоким порядком точности.

Итак, для расчета конвективных слагаемых и первых производных по пространству использовалась конечно-разностная WENO-схема пятого порядка [9]. Поток в точке ( I + 1(2^ записывался в виде суперпозиции потоков

3 г   _ V о(v) f (v)

Ji+1/2    ^^ Ji+1/2, v=1

где Q ⁽¹⁾ = 1/10, Q ⁽²⁾ = 6/10, Q ⁽³⁾ = 3/10 — весовые функции, а соответствующие выражения для потоков имели вид:

• (1)     11      72

J i'+1/2 л J i f Ji-1 + r J i-2, 666

f ^(v) =< ^Ji +1/2

• (2)  251

Ji+1/2    ^Ji+1 + r Ji f-i-1, f +31/2 =-7 f+2 +T f+1 +"7 f. 666

Веса линейной комбинации выбирались так, чтобы они были малыми для разностных шаблонов, содержащих разрывы, и близкими к оптимальным весам Ом в областях, где решение гладкое [10]:

^f i +1/2    ^ ^{ш   f} i +1/2

v=1

to

(v)

G ^{( v )}

G ⁽¹⁾ +G ⁽²⁾ +G ⁽ 3) ’

_    Q ^{( v )}

(б + IS(v)) p

В выражении (4) обозначено: IS ^{( v )} — индикаторы гладкости, для которых в работе [11] предложены выражения:

IS ^<Г* _ 13 ( f - -2 - 2 f - -1 + f ) 2 + 4 ( f -2 - 4 f -1 + 3 f ) 2 , is ⁽²⁾ _ 13 ( f -1 - 2 f + f +1 ) ² + 4 ( f -1 - f +1 ) ², IS^m _ 13 ( f - 2 f +1 + f +2 ) 2 + 4 ( 3 f - 4 f +1 + f +2 ) ²;

p — показатель степени, принимался равным 2; б — малая величина, предотвращающая деление на 0, составляла 10-6. С оптимальными весами WENO-схема эквивалентна несимметричной разностной схеме пятого порядка f _ -3f+2 + 30f+1 + 20f - 60f -1 +15f-2 - 2f -3

d x                      60 A x                    '

Все вышесказанное относится к случаю, когда df рии >  0 (здесь и — искомый параметр). Но знак этой производной может меняться, поэтому в описанную последовательность нахождения потока f _{+ 1/2} вносятся некоторые дополнения. Необходимо сначала расщепить поток на положительную и отрицательную части:

f ( и ) _ f ⁺ ( и ) + f ^- ( и ),

. 0,        ^Т , 0, ди             ди затем по отдельности к f+ и f- применить процедуру аппроксимации с симметричными относительно (i + 1/2) шаблонами. Суммарный поток вычисляется как f+1/2 _ f+1/2 + f-1/2. Расщепленные потоки строятся обычно в виде:

^f ± ^{( и} ) ^_ 2 ( ^{f ( и} ) ±^{Л и} ) ,

Л _ max| f'(и)|, где при определении Л максимум может устанавливаться либо по соседним с точкой i точкам, либо по всем точкам сетки, либо быть константой.

Далее, уменьшение индекса на единицу и выполнение аналогичного комплекса действий позволяет найти суммарный поток f _{- 1/2} _ f +_1/2 + f -_1/2 . Таким образом, первая производная d f /5 x аппроксимируется выражением ( f _{+ 1/2} - f _{- 1/2} )/ A x с высоким порядком точности.

Вязкие потоки, содержащие смешанные производные, вычисляются по схеме WENO с пятым порядком точности. Диффузионные слагаемые из уравнений (1)–(3), включающие вторую производную

• _ _              _                             - . f д д и д ² и )

по пространству, записываются в неконсервативной форме--= ——  и аппроксимируются

(дx дx   дx2 J

центральными разностями с высоким порядком точности на симметричном шаблоне. На 9-точечном шаблоне вторая производная д2и/дx2 аппроксимируется выражением с восьмым порядком точности:

д ² u i " x x²

'В (it-

/ v Рm \^i + m   i—i-m     ^i / m=1

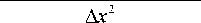
f 8 д ¹⁰ u, )

+ O A x -- :t- .

(       дx10 J

Разложение u i _{- 4} , .., u i-1 , u i _{+ 1} , .., u i ₊ 4 в ряд Тейлора в окрестности i -й точки и объединение коэффициентов при производных одного порядка дает систему линейных алгебраических уравнений для нахождения неопределенных коэффициентов в m :

в 1 + 4 0 2 + 9 в з + 16 0 4 = 1,

<01 + 16 0 2 + 81 в з + 256 0 4 = 0, ” 0 1 + 64 0 2 + 729 0 3 + 4096 0 4 = 0,

01 + 256 в 2 + 6561 в ₃ + 65536 0 4 = 0.

Полученные из ее решения коэффициенты имеют значения: 0 1 = 1,6, 0 ₂ =- 0,2, в ₃ = 0,02539682, в ₄ =- 0,00178571. Тогда разностное соотношение (5) приобретает вид: д ² u , /дx ² =[ 1,6 ( u , _{+ 1} + u , 1 ) -- 0,2 ( u_{i + 2} + u_{i - 2} ) + 0,02539682 ( u_{i + 3} + u_{i - 3} ) - 0,001785712 ( u_{i + 4} + u , _{- 4} ) - 2 - 1,4236111 - u , ]/A x² .

Представленный метод нахождения производных по пространству позволяет интегрировать уравнения (1)-(3) на 9-точечном шаблоне с высоким пятым порядком точности, хотя часть производных считается с более высокой точностью (вычислительный шаблон обеспечивает это, и качество расчетов, по крайней мере, не ухудшается). Аналогичные рассуждения приводят к тому, что теоретически порядок точности можно повысить до любого требуемого, если соответствующим образом расширить разностный шаблон.

Для аппроксимации потоков на границе в рассмотрение вводятся «мнимые узлы». Значения параметров экстраполируются в эти точки со вторым порядком точности.

По времени уравнения (1)–(3) интегрировались со вторым порядком точности. TVD-схема Рунге–Кутты второго порядка, используемая в работе, выглядит следующим образом [12]

U ⁽¹⁾ = U n +A t L( U n ),

U ⁽ n ^{+ 1)} = 1 U n + 1 U ⁽¹⁾ + 1 A t L( U ⁽¹⁾).

22  2

Здесь L — конечно-разностная аппроксимация.

Таким образом, методика расчета заключается в объединении идеи WENO, метода центральноразностных аппроксимаций высокого порядка и TVD-метода Рунге–Кутты.

4. Результаты параметрического исследования

Рассмотрим модельную задачу торможения сверхзвукового течения в плоском канале квадратного сечения. При дозвуковом протекании вязкого газа сквозь канал картина течения достаточно ясна: входящий поток содержит на стенках пограничные слои, толщина которых растет в продольном направлении, далее (при достаточной длине канала) слои сливаются. Торможение течения у стенок и увеличение толщины погранслоев вызывает разгон в ядре потока (вследствие выполнения условий сохранения), при этом поперечный размер ядра уменьшается.

Иная ситуация возникает при входе в канал сверхзвукового потока. Здесь на стенках также образуются пограничные слои, но прежний баланс между формирующимися слоями и центральным ядром потока отсутствует. Режим реализующегося течения становится закритическим и имеет сложную структуру с системой трансформирующихся скачков и градиентов параметров. Далее покажем, как в зависимости от числа Маха меняется структура течения, представим сложную картину скачков и зон разряжения в плоскости симметрии для различных значений числа Маха. Отметим, что нестационарное течение стабилизируется со временем.

При числе Рейнольдса 10⁶ и числе Маха 1,2 была проанализирована сходимость численного решения при квантовании по пространству. Для этого сравнивались полученные на различных по мощности сетках значения продольной компоненты скорости U . Графики распределения скорости при различных сетках в момент времени, равный 4 безразмерным единицам, приведены на рисунке 3. Переход с сетки с 50 400 800 узлами к сетке с 90 601 000 узлами незначительно меняет результат, вследствие этого сетку 800 х 251 х 251 считаем приемлемой для расчетов. Важно, что продвижение вверх по числу Рейнольдса потребует дополнительного анализа и обеспечения асимптотической сходимости как по порядку точности аппроксимации, так и при квантовании по пространству. Возможно, более целесообразным окажется осуществление расчета для невязкого газа (в дальнейшем невязкого расчета).

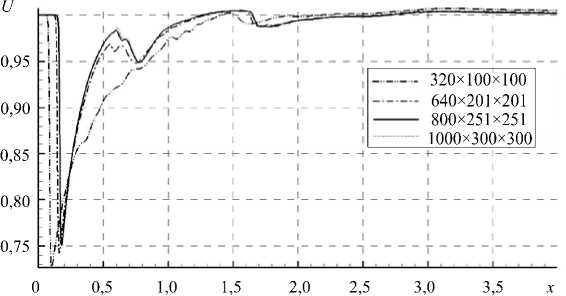
Рис. 3. Распределение продольной компоненты скорости на оси симметрии канала для различных сеток

При численном решении дифференциальных уравнений гидромеханики с использованием явной разностной схемы, как в рассматриваемом случае, на первый план выходит проблема устойчивости вычислительного процесса. При этом единого критерия устойчивости не существует. Условие Куранта–Фридрихса–Леви является лишь необходимым, но не достаточным. В этом случае шаг по времени определяется на основе методических расчетов и оказывается мал (на порядок или несколько меньше шага по пространству). В данной работе шаг A t по безразмерному времени равнялся 0,0002. При такой его величине, с учетом того, что расчет по времени ведется со вторым порядком точности, нет необходимости обсуждать вопрос о сходимости вычислительного процесса путем уменьшения A t . При решении уравнений гидромеханики для высоких чисел Рейнольдса величина шага интегрирования по времени определяется исключительно условием обеспечения устойчивости вычислительного процесса.

На рисунке 4 показано влияние числа Рейнольдса на распределение продольной компоненты скорости при фиксированном значении числа Маха; расчеты выполнены на сетке 800 х 251 х 251. Здесь и на последующих рисунках 5 и 6 данные вычислены в момент безразмерного времени, равный 15 единицам, когда течение близко к установлению.

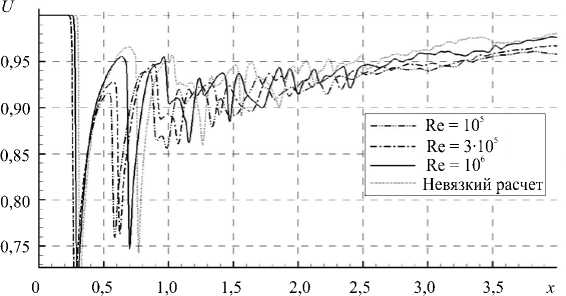
Рис. 4. Распределение продольной компоненты скорости на оси симметрии канала при различных числах Рейнольдса и M = 1,3

Для однопараметрического исследования торможения сверхзвукового потока в прямоугольном канале проведена серия расчетов течений с различными характерными числами Маха при одном и том же значении числа Рейнольдса (см. Рис. 5, где показано распределение плотности на оси симметрии канала). Число Маха увеличивалось за счет повышения скорости потока, при этом для сохранения того же значения числа Рейнольдса предполагалось сужение канала.

Итак, из рисунка видно, что при числе Маха, большем единицы, нестационарный набегающий сверхзвуковой поток тормозится и со временем стремится к установлению. При M = 1,2 на некотором расстоянии от входа в канал формируется прямой скачок уплотнения; далее по потоку параметры изменяются практически монотонно, стремясь к значениям на входе, хотя и присутствуют локальные экстремумы. С повышением числа Маха в канале начинает формироваться и трансформироваться система скачков, которые приобретают икс-образную структуру. Меняется поведение параметров: кривые распределения плотности при M = 1,3 носят явно немонотонный характер; за первым скачком на оси симметрии канала следуют другие скачки с постепенным уменьшением отклонения от значений на входе.

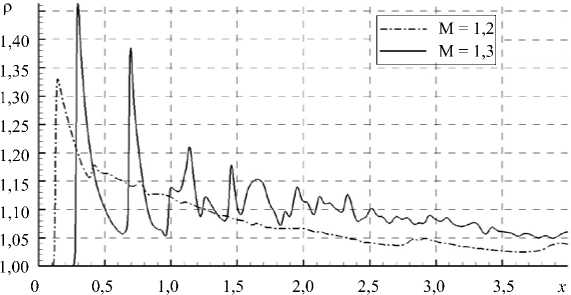
Рис. 5. Распределение плотности на оси симметрии канала при различных числах Маха и Re = 10⁶

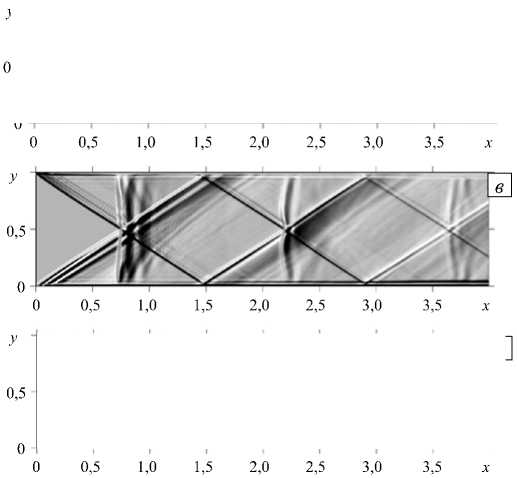
Рис. 6. Теневая картина распределения плотности при различных значениях числа Маха: 1,5 ( а ); 1,7 ( б ); 2,0 ( в ); 2,5 ( г )

При дальнейшем увеличении числа Маха обозначенная тенденция только усиливается, что демонстрирует рисунок 6, на котором показаны теневые картины распределения плотности, отвечающие различным числам Маха. Последовательность «ромбов», которые формируются системой отраженных ударных волн, становится более выраженной, а сами «ромбы» вытягиваются в направлении движения потока. Видно, что прямой скачок в окрестности входа с ростом числа M «отодвигается» вглубь канала, икс-образные структуры скачков укрупняются и становятся вытянутыми.

Сравнение рисунков 1и 6 свидетельствует о физическом подобии картин и подтверждает обоснованность применяемой вычислительной методики.

На основании вышесказанного можно сделать вывод, что представленный способ интегрирования уравнений гидромеханики является эффективным средством теоретического изучения высокоскоростных течений вязкого газа. В работе рассмотрен процесс торможения сверхзвукового течения в прямоугольном канале при различных значениях одного параметра — числа Маха. Показано, как с изменением его значения трансформируется картина течения, образующаяся в результате сложного взаимодействия скачков уплотнения, как икс-образные структуры вытягиваются в направлении течения и увеличивается расстояние между псевдопрямыми скачками.

Работа выполнена при финансовой поддержке Программы фундаментальных исследований УрО РАН (проект № 12-T-1-1006) и РФФИ (проект № 13-01-96004-р_урал_а).