Применение SIR модели в моделировании эпидемий

Модель SIR (модель Кермака-Маккедрика) - одна из простейших ком-партментных моделей, в которых с помощью систем дифференциальных уравнений описывается динамика групп восприимчивых, инфицированных и выздоровевших индивидов. Многие модели являются производными от этой базовой формы. Модель состоит из трех «ячеек». S: количество лиц, восприимчивые к инфекции, то есть, те люди, которые не имеют иммунитета к данному вирусу и потенциально могут заразиться. I: число инфицированных в некоторый момент времени. Это инфицированные люди, способные заразить восприимчивых людей. R: количество людей, которые переболели, имеют иммунитет, или число умерших лиц. То есть, это люди, которые были инфицированы и либо вылечились от болезни и попали в удаленный отсек, либо умерли. Такой моделью можно пользоваться для расчета таких показателей, как распространение болезни, общее число инфицированных или продолжительность эпидемии, а также оценить различные эпидемиологические параметры, такие как репродуктивное число. Такие модели могут показать, как различные меры общественного здравоохранения могут повлиять на исход эпидемии, к примеру, какой метод является наиболее эффективным для выпуска ограниченного количества вакцин для данной группы населения или то, как влияют меры предосторожности на скорость распро- странения инфекции. Эта модель достаточно предсказуема для инфекционных заболеваний, которые передаются от человека к человеку, и когда выздоровление вызывает устойчивую резистентность, таких как корь, эпидемический паротит и краснуха.

Итак, мы имеет три изменяющие во времени величины:

S(t), I(t),R(t)

Для любого момента времени сумма этих трех значение равно общей численности популяции:

S(t) + I(t) + R(t) = N (1)

Для примера рассмотрим начальный момент времени, т.е., начало эпидемии. Пусть у нас имеется один инфицированный индивидуум и некоторое количество восприимчивых людей. В результате контактов, данный инфицированный заражает какое-то количество восприимчивых, тем самым переводит их из «ячейки» S(t) в «ячейку» I(t). Пусть один инфицированный заразил в среднем за единицу времени троих людей. Тогда новую величину обозначим через в — интенсивность заражения, и она равна в = 3. Дальше рассмотрим середину эпидемии. В популяции, кроме двух упомянутых категорий людей, появились переболевшие или выздоровевшие. Рассмотрим конкретного инфици- рованного и посмотрим, сколько людей он может заразить, это уже не будет значение β, потому что у нас в популяции есть люди невосприимчивые к данной инфекции, поэтому значение β надо уменьшить, то есть, надо умножить на долю всех восприимчивых людей в данный момент времени в популяции:

β ∗ S(t) (2)

Таким образом (2) это и есть количество инфицированных людей за единицу времени одним конкретным человеком.

Общее количество всех инфицированных за единицу времени увеличивается на величину:

β ∗ S(t) ∗ I(t) (3)

Конечно, реальное значение (3) будет несколько отличаться от наших вычислений, оно будет меньше, так как, разные инфицированные могут заразить одного и того же человека, но мы этим пренебрежём.

Напомним, что изменение величины за единицу времени это и есть ее производная. Таким образом, мы можем записать, что:

dS(t) = -β ∗ S(t) ∗ I(t)            (4)

dt           N

Итак, общее количество восприимчивых индивидуумов за единицу времени уменьшается на данную величину, поэтому спереди ставим знак « - ». На эту же величину увеличивается число инфицированных людей за единицу времени, но с некоторыми изменениям:

dI(t) = β∗S(t)∗I(t)-γ∗I(t) (5)

где γ-интенсивность выздоровления. Оно выражает количество людей, которые выздоравливают и переходят в ячейку «R» за единицу времени. Например, если болезнь длится 14 дней, и в течение этого периода инфицированный индивидуум может заразить еще кого-то, то γ = 1⁄ . В среднем одна четырнадцатая всех инфицированных переходит в категорию выздоровевших за единицу времени, в нашем случае за один день [1].

Количество выздоровевших за единицу времени:

dR(t) dt

= γ ∗ I(t)

Таким образом, уравнений, которая странение эпидемии:

мы нашли систему описывает распро-

dS(t) = -β ∗ S(t) ∗ I(t)

dt           N dI(t)         S(t)

= β ∗    ∗ I(t) - γ ∗ I(t)

dR(t) dt

=γ∗I(t)

Добавить начальные условия, это значения функции в начальный момент времени:

S(0) = S0 ≈ N

I(0) = I0 ≪ N         (8)

R(0) = R0 = 0

Мы получили задачу Коши. Таким образом, мы при помощи математической модели упрощенно рассмотрели распространение эпидемии.

Рассмотрим аналитически, как будет выглядеть наша модель распространения заболевания. Возьмем отрезок времени в 100 дней. В начальный момент времени доля инфицированных 0%. Зададим % зараженных в нашей группе людей. Пусть β=0,5, а γ= 0,3 (рис 1).

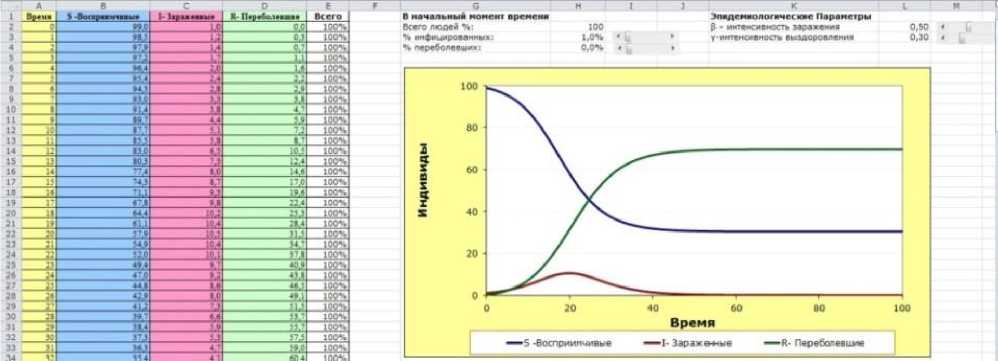
Рисунок 1. При β=0,5, а γ= 0,3

Мы видим, что количество восприимчивых со времен уменьшается, число переболевших увеличивается, а число зараженных достигает своего пика на 20 день, а затем их количество уменьшается. В реальной жизни происходит такой же процесс. Это говорит о том, что количество переболевших, т.е. имеющих иммунитет, быстро растет, соответственно число зараженных уменьшается. Это и есть коллективный иммунитет, когда население становится невосприимчивым к штампу вируса.

Примечание, данная модель является базовой, здесь мы не рассматривали вероятность вакцинации населения, то есть коллективный иммунитет был приобретен естественным путем, к тому же мы, по модели SIR, в число выздоровевших относятся люди, которые погибли от данного заболевания. Это является одним их минусов данного моделирования. Базовая модель

SIR служит отправной точкой для разработки более сложных моделей, включающих такие характеристики, как демографические группы с различными рисками для здоровья, влияние мер общественного здравоохранения, естественные показатели рождаемости и смертности и влияние сто-хастичности (случайности).

В мире появляются новые возбудители болезней, которые могут привести к эпидемии, есть также множество инфекционных заболеваний, которые человечеству еще предстоит победить, но и наука не стоит на месте, развивается, появляются новые методы выявления и борьбы с инфекционными заболеваниями, здесь велика роль математики и математического моделирования. Данная тема является очень обширной и актуальной, особенно в контексте нашего времени, когда вот уже два года мир, человечество страдает от коронавирусной инфекции.