Применение системы Matlab к решению задач сопротивления материалов

 через коэффициенты а и Ь, зная, что корни этого уравнения образуют арифметическую прогрессию.

Решение: Поскольку корни x_v х₂, х₃ уравнения образуют арифметическую прогрессию, то удобно их обозначить так: %, = к - d, х₂ = к, х₃ = к + d В силу этих обозначений находим х, + х₂ + х₃ = Зк , а на основании формулы

Виета имеем х, + х₂ 4- х₃ = -а

Из двух предыдущих равенств следу-

7 -  ° ет, что К — —~ 3

но так как х₂ = к , то

а

Подставив этот корень в данное уравнение, получим

(-|)3+^(-j)2+6(-j) + C = 0.

9аЬ-2а" откуда с = ---—---

9аЬ-2а"

Ответ: с =---------

19-е занятие. Итоговое повторение. Зачет.

Подчеркнем, что экспериментальное апробирование всех разработанных материалов проводилось нами в трех типах школ (естественно-техническом лицее, малой школьной академии и в математических классах школы № 32 г. Саранска).

ПРИМЕНЕНИЕ СИСТЕМЫ MATLAB К РЕШЕНИЮ ЗАДАЧ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

Сопротивление материалов как одна из важнейших дисциплин играет существенную роль в подготовке инженеров любых специальностей и входит в программу обучения студентов вузов большинства технических факультетов.

На основных принципах сопротивления материалов базируются такие дисциплины, как строительная механика, строительные конструкции, теория машин и механизмов, детали машин. В различных курсах по машиностроительным, механическим,строительным, приборостроительным и другим специальностям также широко используются важнейшие положения сопротивления материалов.

Главной задачей дисциплины является исследование напряженно-деформированного состояния элементов на различных стадиях нагружения внешней нагрузкой. Хорошее усвоение студентами курса сопротивления материалов предполагает не только глубокое изучение теории,но и приобре тение твердых навыков в решении задач и проведении исследований. При этом очень важна визуализация их результатов, что не всегда осуществимо вручную, и требуется развитие методов исследования напряженно-деформированного состояния материалов.

Исследование напряженно-деформированного состояния материалов с помощью методов теории упругости предусматривает решение необходимого количества уравнений механики, с помощью которых могут быть определены тензоры напряжений, перемещений и деформаций. Этими уравнениями являются:

• а)    дифференциальные уравнения равновесия (Новье), устанавливающие общие условия равновесия внутренних усилий в элементах;

• б)    статические условия на поверхности тела (граничные условия), используемые для определения постоянных интегрирования, появляющихся при интегрировании уравнений (а);

ЖЖЖЖ ИНТЕГРАЦИЯ ОБРАЗОВАНИЯ

• в)    геометрические уравнения (Коши), выражающие зависимость между перемещениями и деформациями;

• г)    уравнения неразрывности деформаций (Сен-Венана), устанавливающие связь между деформациями в различных плоскостях;

• д)    физические уравнения (Гука), определяющие зависимость между напряжениями и деформациями.

С помощью указанных уравнений определяются как функции координат точек составляющие тензора напряжений, составляющие вектора перемещений и составляющие тензора деформаций. Таким образом, необходимо решить систему из 9 уравнений в случае плоского, и из 15 уравнений в случае объемного напряженно-деформированного состояния, что практически невозможно без применения средств вычислительной техники. Поэтому в конечном счете решаемая задача представляет собой более или менее сложный программный продукт. Разумеется, как и любая другая программа, она может быть реализована на любом универсальном языке программирования. Однако и в этом случае на пути исследователя возникает следующая проблема: требуется знание не только предметной области исследуемого объекта, но и языка программирования, причем на достаточно высоком уровне.

Реализация таких возможностей на универсальном языке программирования очень непроста. Вместе с тем в настоящее время на российском рынке компьютерных технологий есть программный продукт, позволяющий весьма эффективно решить указанную проблему, - пакет MATLAB 5 * (название произошло от словосочетания Matrix Laboratory).

Пакет MATLAB - это уникальное сочетание возможностей математики с последними достижениями в области вычислительной техники. Основное его достоинство заключается в том, что для работы пользователю достаточно знать о нем ровно столько, сколько требуется для решения поставленной задачи. Например, в простейшем случае MATLAB может сыграть роль обыкновенного калькулятора, для использования которого достаточно помнить знаки математических операций. Если же решаемая задача требует создания каких-либо специальных инструментов, MATLAB предоставляет в распоряжение пользователя универсальный язык программирования, обеспечивающий проведение исследований практически во всех известных областях науки и техники.

Покажем решение задачи о распределении напряжений в сечениях д линной балки, свободно опертой на две опоры, при ее изгибе.

Балка длиной /, высотой h загружена по верхней кромке равномерно распределенной нагрузкой q (рис. 1). Толщину длинной балки можно считать достаточно малой по сравнению с другими ее размерами, поэтому задача исследования напряженно-деформированного состояния в данном случае является плоской. В случае плоской

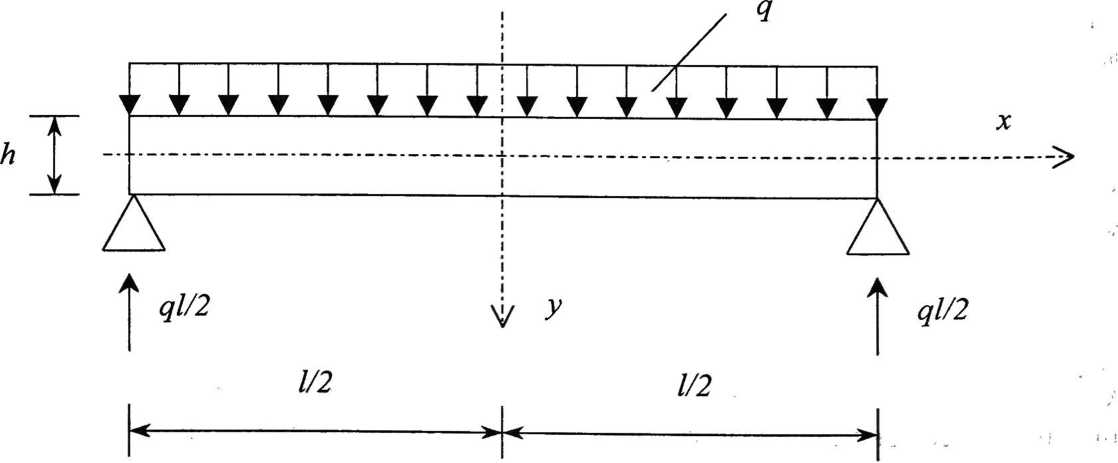
Рис. 1. Расчетная схема балки

задачи напряжения и деформации не зависят от координаты Z, следовательно, основные уравнения теории упругости упрощаются и их число сокращается.

Функция распределения напряжений, выбранная для решения задачи, имеет вид

и удовлетворяет бигармоническому уравнению плоской задачи V⁴ f = 0.

Для исследования плоского напряженного состояния выделим из тела элементарную площадку dxdy. Укажем нормальные и касательные напряжения, действующие в сечении (рис. 2), выразив таким образом напряжения в некоторой точке через напряжения в бесконечно малой площадке.

Рис. 2. Напряжения в сечении балки

Составим для данной площадки усло

вия равновесия:

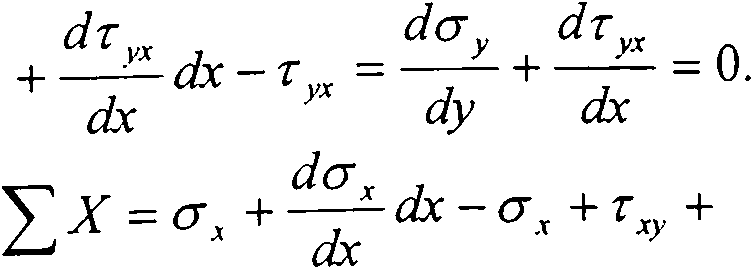
dr,y J т — dy тху dy do^ ! dr^ dx dy

Согласно правилу парности касательных напряжений ф_ху = ф^ для решения плоской задачи теории упругости достаточно определить три составляющие тензора напряжений: у_х, у и ф_х . С учетом этого условия равновесия (Новье) принимают вид

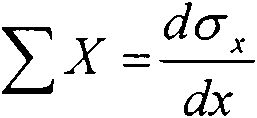
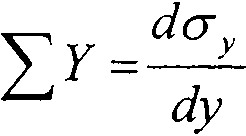
dT dy dT [ ух dx

Статические условия на поверхности тела также предстают в виде т! + ^Л1 = УУ-ух        у       S •

Геометрические уравнения (Коши) в случае плоской задачи:

dU

£X "     ,   ’ dx dV

dy ’ dV du

dx dy

Из уравнений неразрывности деформаций (Сен-Венана) остается одно уравнение:

dy" dx2 dxdy

Закон Гука предстает в следующем виде

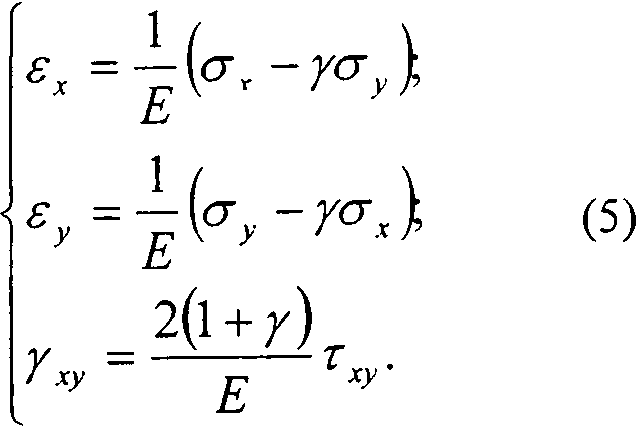
С помощью этих уравнений должны быть найдены как функции координат точек три составляющие тензора напряжений.

По формулам Эйри находим выражения для напряжений:

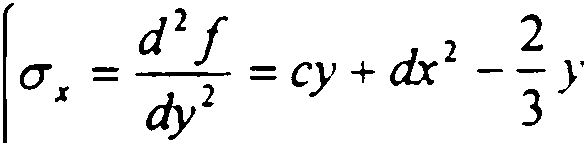
х = ± 1/2. N = О, М = 0. Q = ± qlC.

С учетом этих условий выражения для напряжений принимают вид

^7 к ^d з

7 = —у = а*Ьу + -у ;

ах            3

т = - 7 - = -Ьх + dxy" dxdy

Для нахождения постоянных a. b. с. d воспользуемся граничными условиями задачи:

на верхней грани:

у = h/2, yt= -q, фху=0;

на нижнеи грани:

у = h/2, уч= 0. фху=0;

для торцов балки:

координата сечения х, м

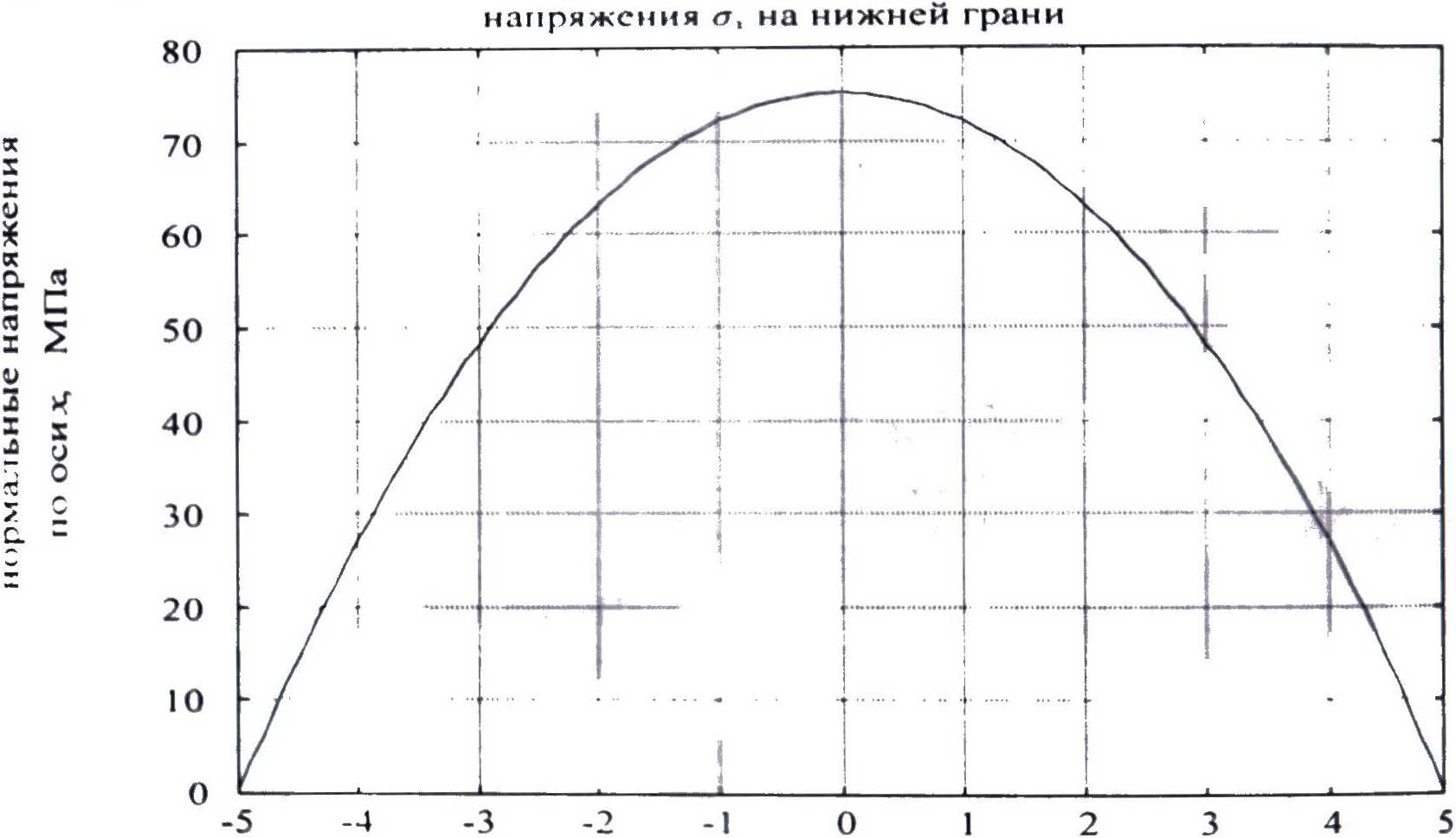
Рис. 3. Зависимость величины нормальных напряжений о, на нижней грани балки от координаты сечения х

Для построения графиков распределения нормальных напряжений ух по верхней и нижней граням балки решаем уравнение f при > = +h/2 и \ = -Н2; значения координаты х меняем в пределах от - 1/2 до +1/2.

Сформируем м-функцию для описания правой части уравнения f, под именем fun 1: function fl =fun l(x.v,q.h,l);

fl=6*q*((2 3)*(у'Л2/ЬЛ2)-(!/10))*Ь h)+6*q*U A2/h л2)*(( 1 '4Цх л2/1.л2))*(у h);'

М-сценарий fun 11 решения уравнения f при переменном x:

хЦ-5:0 1 5];

У=0-5;

q=i;

h=l;

1=10;

zl=funl(x,y,q.h,l);

figuref 1 ),plot(x^ 1, ’b’ Xgridлlabe^Гюopдинaта сечения Х”),у1аЬе1(“нормаяьные напряже ния по оси X”),... tit

Результаты представлены на рис. 3. 4

Для построения графиков распределения нормальных напряжений ) по сечению балки решаем уравнение 1. при переменном у.

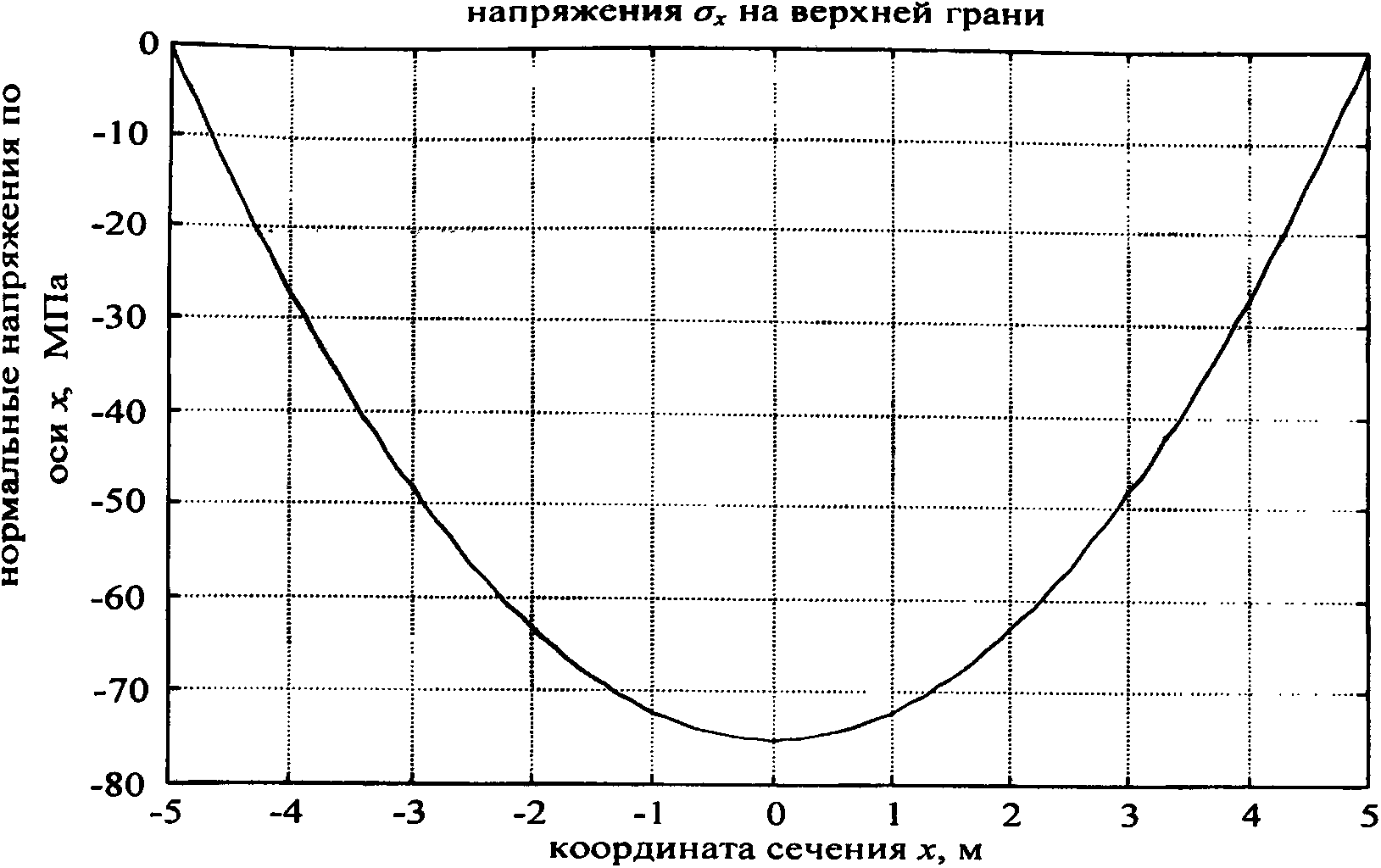
Рис. 4. Зависимость величины нормальных напряжений о_х на верхней грани балки от координаты сечения х

Сформируем м-функцию для описания правей части уравнения ^ под именем fun2: function f2=fun2(y,q,h);

f2=-(1 /2)*q*( 1 -3 *(y/h)+4*(y.A3/h Л3));

М-сценарий fun22 решения уравнения f2 имеет вид y=[-0.5:0.01:0.5];

q=i;

h=l;

z2=fun2(y,q,h);

figiire(2),plot(y^/b’),grid^abel(‘‘i«x)^^

сечения У”),у1аЬе1(“нормальные напряжения по оси У”),... 1к1е(“нормальные напряжений уу в сечении”)

Результаты решения представлены графиком на рис. 5.

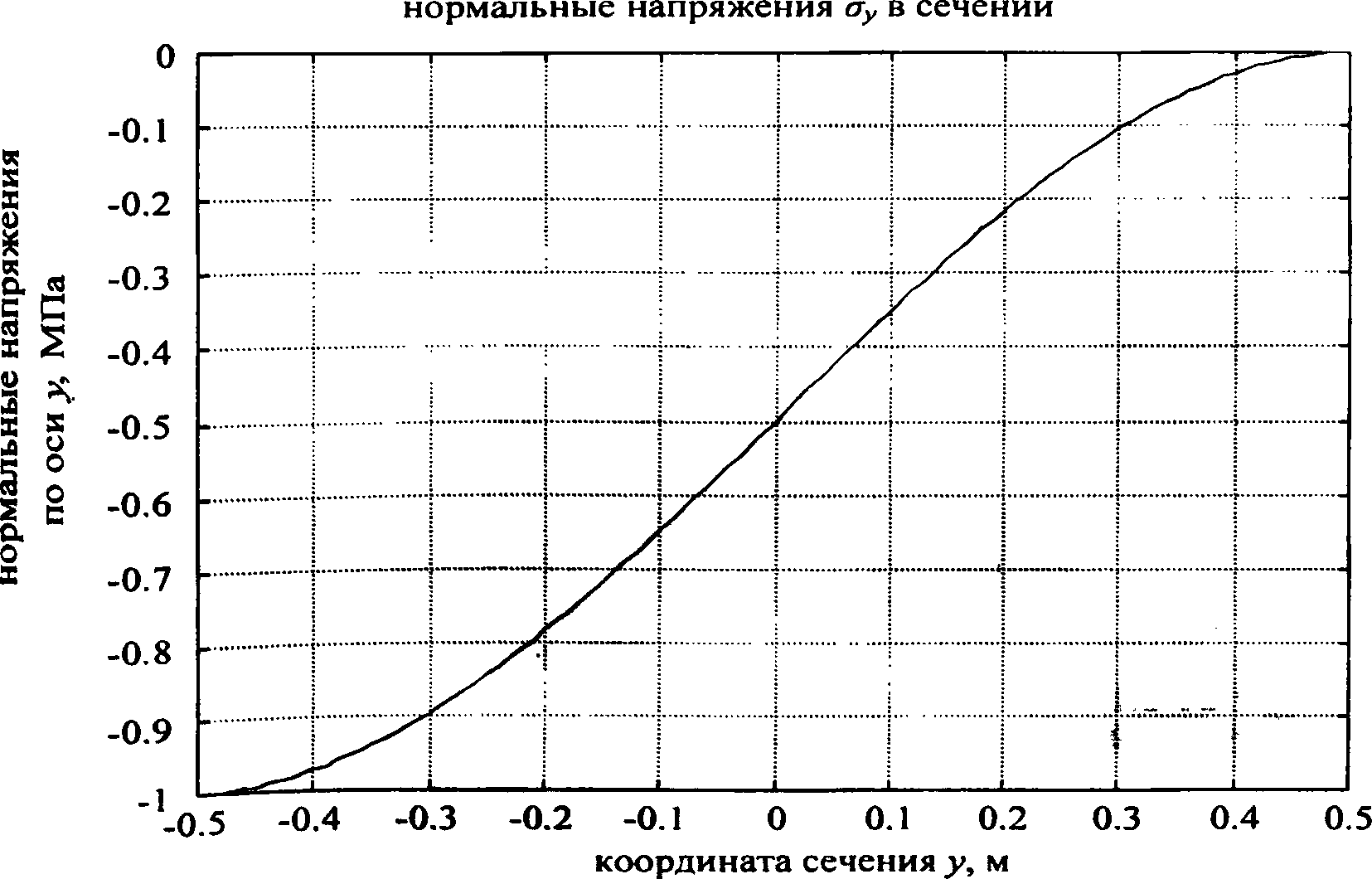
Рис. 5. Распределение нормальных напряжений о_у по сечению балки

^%^^     ИНТЕГРАЦИЯ ОБРАЗОВАНИЯ ^^

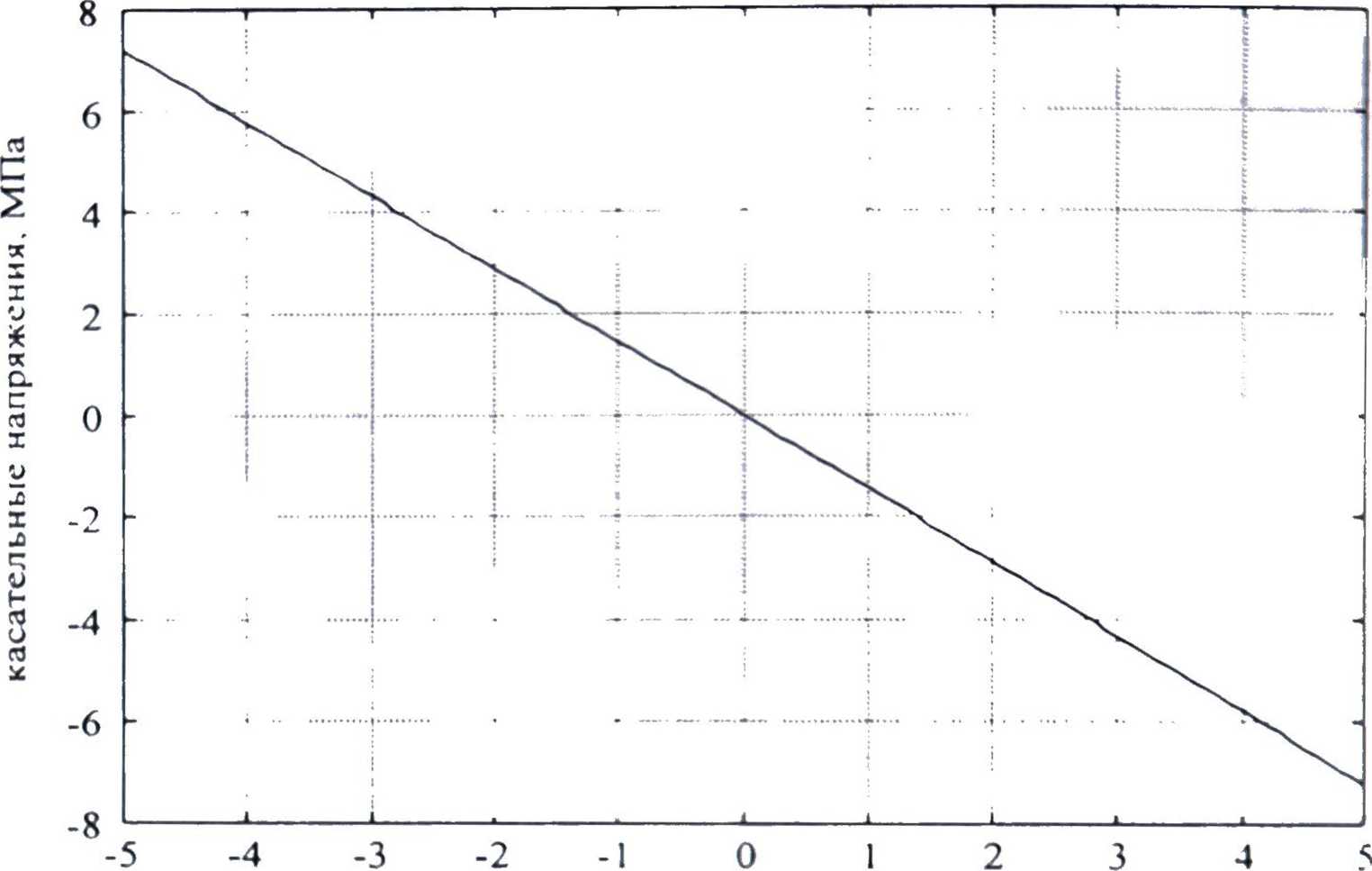
Для построения графиков распределения касательных напряжений ф по верхней и нижней граням балки решаем \ равнение f3 при у = -ьЬ/2 и у = -h/2; значения координаты х меняем в пределах от-12 до-12.

Сформируем м-функцию для описания правой части уравнения f пол именем fun3:

напряжения го на верхней грани

координата сечения х.м

Рис. 6. Зависимость величины касательных напряжений rt> на верхней грани балки от координаты сечения д

координата сечения х. м

* Зависимость величины касательных напряжений r_t> на нижней грани

балки от координаты сечения х

function f3=fun3(x,y,q,h);

f3—(3/2)*q*( 1 -4*(y.A2/h.A2))*(x/h);

М-сценарий решения fun33 имеет вид x=[-5:0.1:5);

У=0.5;

q=i;

h=l;

z3=fun3(x,y,q,h);

figure(3),plot(x^,^^gridAlabel(“координата сечения X ),у!аЬе1(“касательные напряжения”), ...

Й11е(“напряжения на нижней грани”)

Результаты решения представлены графиками (рис. 6 и 7).

Все графики распределения напряжений построены для балки высотой h = 1 м. длиной I = 10 м, загруженной равномерно распределенной нагрузкой q = 1 кН/м. Чтобы изучить поведение исследуемой системы при других условиях (размерах, внешней нагрузке и т.д.), достаточно в м-сценарии изменить входные параметры.

Таким образом, использование пакета MATLAB позволяет без значительных затрат труда решать задачи сопротивления материалов при исследовании напряженно-деформированного состояния элементов в различных условиях.

КЛИНИЧЕСКОЕ ЮРИДИЧЕСКОЕ ОБРАЗОВАНИЕ

Термин «клиническое юридическое образование» появился в США в 20 - 30-х гг. XX столетия и стал отражением определенного течения в юридическом образовании. Его представляли члены так называемого реалистического юридического движения, старавшиеся внести социальные аспекты в изучение права. Американские юристы клиническое юридическое образование понимали как эквивалент клинического медицинского образования. На самом деле, идея была позаимствована из медицинской профессии, где существовала традиция использовать функционирующие учреждения медицины как базы для подготовки молодых специалистов.

Становление клинического юридического образования в США произошло в 60-х гг. XX в., когда частные фонды стали стимулировать создание клиник, видя в них средство разрешения двоякой проблемы, а именно: оказание необходимой юридической помощи в первую очередь малоимущим клиентам и одновременно формирование необходимых юридических навыков у студентов. На протяжении последующих десятилетий клинические программы получили бурное развитие.

При поддержке, осуществляемой Фондом «Евразия» за счет средств, пре-достав юнны.х Агентством международного развития США (АЮ), с 1-го июня

2000 г. в Мордовском государственном университете им. Н.П. Огарева действует юридическая клиника - бесплатная сту-денческая юридическая консультация.

Цели создания и функционирования данной организации заключаются в повышении профессионального уровня юридического образования на основе оказания бесплатной правовой помощи некоммерческим структурам, предприятиям малого бизнеса, индивидуальным предпринимателям

Задачами проекта «Юридическая кли-ника» являются:

• -    нравственное формирование буду-щего юриста как социально активной личности;

• -    вовлечение студентов в работу с правоохранительными органами и правозащитными организациями, воспитание у студентов традиций принимать самостоятельные решения и отстаивать свою позицию, правильно и качественно выполнять свою работу; перенятие студентами опыта специалистов;

• —    оказание студентами бесплатных юридических услуг;

• -    создание базы юридической клиники;

  -организация пропаганды юридических знаний, формирование) консультируемых навыков самостоятельного обучения современным методикам поиска необ-

  © Т. В. Ху дойкина, 2001