Применение спектрального метода к расчету дисперсии волн регулярных волноводов с произвольным диэлектрическим заполнением

В статье предложен общий подход к расчету дисперсионных характеристик экранированных волноводов с произвольным диэлектрическим заполнением и сложной формой идеально проводящей ограничивающей поверхности. Подход основан на методе Галеркина и на представлении полей волн направляющей структуры в виде разложений по базису функций, обладающих свойством полноты.

Метод расчета

Рассмотрим закрытую направляющую структуру (экранированный волновод) с произвольным диэлектрическим заполнением и произволь-

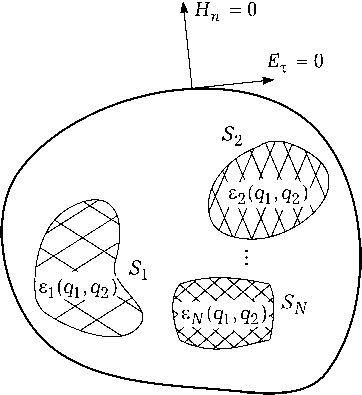
Рис. 1. Произвольная направляющая структура

ной регулярной и непрерывной формой внешней идеально проводящей ограничивающей поверхности (рис. 1).

Геометрия идеально проводящего экрана рассматриваемого волновода описывается обобщенными координатами (qi, q2, z). В качестве примеров возможных вариантов (qi,q2) можно указать канонические системы координат: пря- моугольную, цилиндрическую и эллиптическую. В предлагаемом методе нет ограничений на форму внешней идеально проводящей границы – она может быть как гладкой, так и дискретной, единственным ограничением является существование для заданной формы внешней идеально проводящей границы базиса собственных функций, обладающего свойством полноты.

Полагая, что диэлектрическое заполнение рас- сматриваемого волновода является изотропным и регулярным по продольной оси z, представим значение диэлектрической проницаемости в виде кусочно-непрерывной функции:

^s ( q i , q 2 ) = •

s i ( q i , q 2 ) e S i , S 2 ( q i , q 2 ) e S 2 ,

...

_e N (q1,q 2 ) e SN, запишем уравнения Максвелла для всей области внутри рассматриваемого волновода:

rot ( E ) = - i юц о H i ;

rot ( H ) = i tos ( q i , q 2 ) б д E.

Из системы уравнений (1) получаем уравнение

—*        О /          X —*

rot rotE = k 2 s ( q i , q 2 ) E ,

I

2 E q i H i E 7 7

= ^k0 ^s( q i , q 2 ) E q^ ;

где вектор напряженности электрического поля представляется в виде

E — = ( ^Eq_i ( q i , q 2 ) q i +

⁺ E q ₂ ( , i , q 2 ) q 2 ⁺ E z ( q i , q 2 ) z o ) e ^— i ^{e z} •

Используя обобщенную формулу [1] представления оператора «ротор» в произвольной координатной системе:

H 2

—

d

rot ^{( E )=} H r

⁽ 8 E z 8^{( e}, 2 H 2 ) '

—

+--

H 2 d q 2

V

d z

7

— qi +

1 H E q , H l )_а^ q 2 +

H 1

V

⁺ H i H 2

—

A

z

—

d z

8 q i

7

a ( E q 2 H 2 ) 5 ( e , i H i ) ) -------- — --------

V где H1, H2 – rotrot (E— )

q ₁

a q i

^d q 2

— z,

7

коэффициенты Ламе [1],

получим:

—

H 1 H 2

i

H 2

V

( ^d 2 ( ^e, 2 H 2 ) S² ( E q i H i)( --------- — ---------

^d q i' q 2

V

d q 2     ^

—

" ( ^e, i H i ) 5 2 E z --------- — ----

8 z 2 V

8 q i d z

;

7

rotrot ( E )

dE

—

^d 2 E 2 ^H 2 ) )

H 2 d q ₂ d z V

8 z ²

7

—

— i e^ E z + P ² E_a H I — 8 q 2    ^P q ^{2 2} J

( i ⁵ ( E q 2 H 2 ) )

8 q i H i H 2     8 q i

8 +--

V7

⁽ i (>& i H i ) )

d q 2 H i H

V

^r 2      9 q i

7

+

= ^k 0 ^s ( q i , q 2 ) E q ₂ ;

H 1 H 2

—

V

— i e^ ( E q i H 2 ) —

8 q_i     ^{i 7}

d ( Hi dEz

8 q 2 V H 2 d q 2

— i в

54 d q 2

—

V-2^H 2 ) )

^d q 2

= k o ^s ( q i , q 2 ) E z •

7

При решении системы трех дифференциальных уравнений (4) будем использовать представление искомых компонент поля в виде рядов по некоторому базису функций разложения. Данный базис должен удовлетворять свойству полноты и может быть ортогональным (при этом требование ортогональности не является обязательным).

Кроме того, выбранный базис функций разложения должен обеспечивать выполнение граничных условий на идеально проводящей ограничивающей поверхности волновода S , которые могут быть записаны в следующем виде [2]:

q ₂

	d	(	1	5 ( e, , H 2 )			+
	3 q i	H 1 H 2 V		a q i		7
+	d	(	1	5 ( E q i H i»
	d q 2	V	H 1 H 2	a q i		7	J ;
rotrot		( E ) z ^
	( 8		H 2 C	( E q i H i	) I		d 2 E z
	d q V	1	H i V	d z	7	J J	d q 2

—

— dq 2 V H 2 dq 2

^( H i d E z L ^d 2 ( E q 2 ^H 2 1

E q i L=⁰ ;

⁵ ( E q 2 H 2 )

^d q 2

= 0;

Ezl, = 0.

S

Вид граничных условий (5) обеспечивает автономность разложений компонент поля.

Будем считать, что для рассматриваемого волновода в выбранной системе координат существует набор базисных функций е -q ⁱ ) , е -q ² ) , е nz ) , обладающих свойством полноты и удовлетворяющих граничным условиям на идеально проводящих стенках ограничивающего волновода (рис. 1).

Таким образом, функции выбранного базиса должны удовлетворять соотношениям:

d q 2 8 z

7

Подставив (3) в (2), получаем:

4q ⁱ )|

0,

s

H 1 H 2

i

H 2

V

(8 2 ( E q 2 ^H 2 ) 5 2 ( E , i H i ) ) --------- — ---------

8 q i d q 2

V

8 q 2    _?

+

lim E

N ^®

q ₁

V

N

- t a - e n - q i )

n = 0

I

^ 0

для любого E_q ;

d ( nq ^{2 )} H 2 )

^d q 2

S

= 0,

Подставив (7) в (4), получим систему трех функциональных уравнений, записываемых относительно коэффициентов разложений неизвестных функций:

lim E,

N ^®

V

N

- X b q ^{2 )}

n = 0          у

^ 0

для любого E_q ;

H 1 H 2

^H 2

V

( _N

X bn n=0

d² ( e nq ²) H 2 ) ---------- —

^d q i ^d q 2

e

( z )

n

\ = °' s

lim E

N ^»

V

N

- X    'z )

n = 0        у

N

-X an n=0

d ²

V

( = nq * H i )

d q 2

+

^ 0

у

для любого E_z .

( +

На практике условия (6) могут быть легко реализованы в случае, если форма ограничивающего волновода (рис. 1) соответствует какой-либо канонической системе координат (прямоугольной, цилиндрической, эллиптической и т. д.). Для системы координат, отличающейся от канонической, поиск таких базисных функций представляет собой нетривиальную задачу, которая в основном может быть решена только численным способом [3–4].

В результате неизвестные функции поля будем искать в виде разложений:

N

E q _i ( q i , q 2 ) = X ^an e nq ¹ ) ( q i , q 2 ) ;

n = 0

N

E q ₂ ( q i , q 2 ) = X ^ьп^еПq ² ) ( q i , q 2 ) ;                    ⁽⁷⁾

n = 0

N

Ez (qi' q 2) = X cnenz) (qi, q 2) • n=0

V

N в Hi X anenqi)

n = 0

N

- ieX Cn n=0

) d e nz ))

^d q i

У у

N

= ^k 0 s ( q i ' q 2 ) X ^an e niq ⁱ ) ;

i

H 2

-

n = 0

N       ( z )

- i e X C n ⁸eⁿ

V

d

n = 0

(

i

^d q 2

N

+ e ² h 2 X b n e n = 0

^ .⁽ q 2) n

-

у

d q 2 H i H 2

V

( +-L

d q 2 H i H 2 V

N

X bn n=0

N

X a n=0

d ( e nq ² ) H 2 )

8 ^qi

у

+

d ( e nq ⁱ ) H i ) =

n

8 q 2

у

N

= ^k 0 s ( q i , q 2 ) X b ne^ixq ² ) ;

n = 0

H 1 H 2

V

N ieX an n=0

d^ q ⁱ) H 2 )

^d q i

-

N

X C n n = 0

d ² e nz ) d q 2

-

Отметим, что в качестве базисных функций в разложениях (7) могут использоваться собственные функции так называемого «волновода сравнения» – однородно заполненного волновода с ограничивающим идеально проводящим экраном, полностью идентичным ограничивающей поверхности рассматриваемого волновода. В таком волноводе, как известно, могут распространяться только волны Е- и Н-типа, электрические поля которых можно использовать в качестве базисных функций.

Однако выбор функций разложения в виде собственных функций «волновода сравнения» для данного метода вовсе не является обязательным. В качестве базиса могут использоваться совершенно произвольные функции, удовлетворяющие свойству полноты и граничным условиям (6).

-

N

У c. — ⁿ d _q„

H i s e n )

-

n = 0

^d q 2 V ^H 2 ^d q 2

у

N ieX bn n=0

9 ( e nq ² ) H 2 ) _

8 ^q 2

у

N

= ^k Q s ( q i , q 2 ) X c n e nz ) ;

или

N

X an n=0

n = 0

+

H 1 H 2

d ² ( e n^qi ) H i )

d q 2

+

V

N

'■ He nq ) - X b

2 =

у

n = 0

n H 1 H 2²

d ² ( e nq ² ) H 2 )

^d q i ^d q 2

N

+ ieX c n=0

( z ) e_n

ⁿ H i H 2 d q i

= 0;

N

У а« ~ n я

n = 0

r

i

d q 2 H i H

8 ( e n^qi ) H i )

—

N

— ± bn n=0

V

Г k2s( qi, q 2) enq 2)

8 ^q 2

7

i

⁺ HH 2

d ² ( e n^{q i} ) H i )

8 q 2

H 2

e nq i ) ds

—

V

+ p ² H ₂ e n^{q 2} ) +

—

N

2 bnU^q i )

= 0   5     ^H i ^H

n = 0

S

7

d ² ( e nq ² ) H 2 ) —----dss +

5 q i 8 q 2

r d

■ — ■

d ( e n^{q 2} ) H 2 )

+

—

d q 2 H i H

V

N

— i ₽2 c n=0

n

N

— i P ± a.

n = 0

n

^r 2       8 q i

7

7

N

i pV cnd)e(qi)

² n ^f q H i H 2 d q i

( z )

-n-ds = 0;

n = 0    5

( z )

— £e ^ = 0; H 2 8 q 2

N

2 a n f e qq 2 ^

n = 0    5

i a ( e n^{q i} ) H i ) '

d q 2 H i H

V

8 ^q 2

7

ds —

H 1 H 2

d ( e nq ⁱ ) H 2 ) --------- —

—

N

— i ₽2 bn

a qi d(enq 2) H 2 ) --------- —

± bn $ e q^{q 2} ) ^k2 ^s ( q i , q 2 ) e nq ² )

N

n = 0

S

+ p ² H ₂ e n^{q 2} ) +

n = 0

N

— 2 C n n = 0

H i H 2    d q 2

r

+Л

V d^q 2) H 2 )

A

Г

V

1 2 /        \ ( z ) i d ² e ⁽ z )

^k 0 ^s( q i , q 2 ) ev-n-n- —n - ⁺ H i H 2 d q i

8 q 2 H i H 2

V

a q i

7

ds

+

+

i d

(z)A^i

H i S e r

N                    ( z )

i вУ U < ⁽ q 2 ) -I- *nl ² n ^f ’  ^H 2 ^d q 2

ds = 0;

H i H 2 d q 2 V H 2 8 q 2 ^J

= 0.

n = 0

S

7

N

Для решения дисперсионной задачи и расчета полей собственных волн рассматриваемого волновода воспользуемся проекционной методикой, умножив первое уравнение (8) на функцию e q^qi ) , второе — на функцию e q^{q 2} ) , третье — на функцию e qz ) (здесь q = 0, i, 2, ..., N ) и проинтегрировав по поперечному сечению волновода.

Такой подход представляет собой модификацию метода Галеркина. Отличительными особенностями предлагаемого подхода, обеспечивающими его универсальность, являются применение процедуры Галеркина к функциональным уравнениям, получаемым непосредственно из уравнений Максвелла, и отказ от использования аналитической связи между компонентами поля. Установление взаимосвязи между q ₁, q ₂, z компонентами поля здесь полностью возлагается на коэффициенты разложения a_n , b_n , c_n .

В результате применения спектрального метода получаем систему линейных алгебраических уравнений относительно трех неизвестных вектор-столбцов:

■ i ^e ± a n f ^eqz ) h H n = 0    5 ⁱ

d ( e nq ⁱ ) H 2 )

ds

—

—

—

S

^r 2       ^d q i

iP± bn f eqz) H

= ¹

N

d

( e nq ² ) H 2 )

n = 0

N

S

8 q 2

ds

—

± ^cn f ^eqz ) k > E < q i , q 2 ) e n' ^{) +}

i    5 2 e n z >

n = 0    5

i d

+--

V

H i s e nz ))

H i ^H 2 d q ²

+

H i H 2 d q 2 V H 2 8 q 2 J

ds = 0.

7

Представим (10) в виде системы трех матричных уравнений:

(k2 W(0) + W(i) + P2 W(2)) a — Qb + iPVc = 0;Wa — (c2 Q (0) + Q (i) + p2 Q(2)) b + iPVc = 0;    (ii)

( 0 )       ( i )

—iPWa — iвQb + I k2 V( ) + V() I c = 0,

где

W q n = <£ s ( q i , q 2 ) e q^{q i} ) e n^{q i} ) ^ds , S

Nr

± a n (^ e q^{q i} ) ^k 0 ^s ( q i , q 2 ) e n^{q i} )

+

n = 0    5

Wq(i) =

S¹

d²

(enqⁱH) ds,

^r 2      8 q 2

V

w(²⁾=e (⁴ⁱ) — e⁽qⁱd q,n      q H n

s;

S

d²

Qq,n

(еПq²) H 2 ) ds;

£ ^q  H_iH2   8qiSq2

V

(z ) den/

S

Hi H2 dqi

ds;

W

S

d(enq¹) Hi)

Q(0)

Qq,n

Q(i)

Qq,n

Q(2)

Qq,n

V

dqi HiH 2

V

^dq 2

= J e( qi, q 2 ) eq^{q 2}eqq²)ds^,

S

(

S

dq 2 Hi H

V

ds;

7

d(nq²)H2 )

^{8 q}i

7

ds,

= J eqq²) H₂-Пq²)ds

S

= - (q²) X ^eV. ds;

J q  H 2 8 q 2

Wq,n

^

Q.

V

q,n

_{() i}   д(еП^qi) H 2 )

= (f> e ()---ds

J q Hi H2

-   d(e nq²) H 2 )

ds;

^    -i-2

S

= I- (z) —

I q HiH

q, n =

s(qi,q2 )eqz^)еПzds^, S

V⁽ⁱ⁾ -

Vq, n =

+--

S

d

' i   а²-Пz) +

_VHi H 2 8 qi

Hi ^de nz Л

Hi H2 8q 2 V H2 8q 2

7

7

ds.

Систему матричных уравнений (11) можно представить в виде одного однородного матричного уравнения

a

^- b = 0,

c

где

^ =

k 2 W(0) + W(i) + в2 W(2)

W

- i в W

Q i в V ko2 Q(0) + Q(i) + в2 Q(2) i в V .

- i в Q k02 V (0) + V (i)_

Записывая условие нетривиальности решений системы (11) – приравнивая определитель матрицы ^ нулю, получаем дисперсионное уравнение.

Отметим особенности и преимущества численной реализации предложенного метода.

Из формул (12) видно, что от функции диэлектрического заполнения е(x, у ) зависят только матрицы Q⁽x), Q⁽y) и Q⁽²), которые при этом не зависят ни от частоты, ни от значения продольной постоянного волнового числа в. В результате для сколь угодно сложной структуры (в предложенном методе нет никаких ограничений на характер диэлектрического заполнения) матрицы, входящие в (13), рассчитываются лишь единожды, а затем, при изменении частоты и продольного волнового числа в, они просто домножаются на k2 и в2. Это позволяет существенно сократить время расчета дисперсионных характеристик анализируемой структуры.

Все остальные матрицы в (13) не зависят ни от частоты, ни от структуры диэлектрического заполнения и определяются исключительно геометрией ограничивающей идеально проводящей поверхности (т. е., по сути, формой волновода сравнения). Это также позволяет вычислять их значения один раз и использовать при любых значениях частоты и продольного волнового числа.

Отмеченные особенности представленного метода обеспечивают его существенное преимущество в скорости расчетов по сравнению с методом частичных областей [5] или сеточными методами [6].

Практические результаты применения представленного подхода для частных случаев декартовых координат (при расчете планарных волноводов и прямоугольных волноводов со сложным диэлектрическим заполнением) и радиальных координат (при расчете круглых волноводов со сложным диэлектрическим заполнением) приведены в [7–10]. Все приведенные в указанных работах результаты свидетельствуют о работоспособности и эффективности представленного метода.

Заключение

В общей формулировке с использованием метода Галеркина представлен подход к расчету дисперсионных характеристик экранированных волноводов с произвольным диэлектрическим заполнением. Особенностью подхода является запись компонент поля в виде рядов по набору базисных функций, обладающих свойством полноты и удовлетворяющих граничным условиям на идеально проводящих границах волновода.