Применение спектров высокого порядка при анализе нелинейного взаимодействия высокоскоростного потока газа с твердым телом

При анализе нелинейных свойств сигналов используются спектры высоких порядков: третьего – биспектр, и четвертого – триспектр. Эти функции позволяют определить, какие возмущения являются фазово-связанными, и определить степень этой связи. В силу сложности интерпретации результатов триспектрального анализа экспериментальных данных в аэродинамических исследованиях большее распространение получил биспектральный метод. Впервые этот метод был применен в работе [1]. Подробное описание данного метода представлено в работе [2].

Метод исследований

Спектры высокого порядка определяются через кумулянты второго c 2 ( k ) и третьего c 3 ( k, l ) порядков следующего вида:

c₂ ( k ) = E { x * ( n ) x ( n + k ) } ;

c ₃ ( k , l ) = E { x * ( n ) x ( n + k ) x ( n + l ) } , где E {} - функция математического ожидания; x ( n ) - измеряемый сигнал; индекс «*» обозначает комплексное сопряжение. Выражения для спектра мощности P(f) и биспектра B(f _ ,f 2 ) записываются через кумулянты путем преобразования Фурье:

P ( f) = Е c 2 ( k) exp(i2 n k) = E { X * ( f) X ( f ) } ;                         (1)

k

B ( f , , f 2 ) = E c 3 ( k , 1 ) exp(i 2 n ( f , k + f 2 l)) = E { X * ( f , + f ₂) X ( f , ) X ( f 2 ) } ,                (2)

k, l где X(f - Фурье-преобразование сигнала x(n).

Спектр мощности и биспектр являются спектрами соответственно второго и третьего порядка, представляя собой частные случаи спектра N-го порядка. По значениям биспектра можно определить степень квадратичной связи по фазе волн с частотами f., f2 и f = f _ +f2. Этот параметр можно интерпретировать как вклад энергии нелинейного взаимодействия волн с частотами f _, f2 в энергию волны с частотой f3 = f _ +f2 вследствие резонанса (в данном случае трехчастотного), возникающего при фазовой связанности волн. Биспектр обладает следующими свойствами симметрии:

B(f . , f 2 )= B(f 2 , f )=B*(f . , -f _;)= B*(-f 2 , - f>B(-f 1 - f 2 , f 2 )=B(f_л - f 1 - f )=B(-f 1 - f 2 , f . )= B(f 2 , - f 1 - f )      (3)

Поэтому, используя соотношения (3), при анализе биспектра достаточно знать его значения в треугольнике (0,0), (fN,0), (fN/2, fN/2), где fN - частота Найквиста. Кроме свойств сим метрии важно отметить, что кумулянт третьего порядка равен нулю для сигнала с Гауссовым распределением. В данном случае биспектр будет равен нулю для всех/1,f2.

Поскольку амплитуда биспектра (2) зависит от амплитуды волн, то его обычно нормируют на спектр мощности (1), получая при этом коэффициент (амплитуду) бикогерентности:

bic ²( f i , f 2 ) =

I B ( f 1 , f 2 )Г

P ( f 1 ) P ( f 1 ) P ( f 1 + f 2 )

Величина амплитуды бикогерентности варьируется в диапазоне от 0 до 1, где значение «0» соответствует независимым волнам, а «1» - полностью связанным волнам.

После вычислений значений амплитуд бикогерентности для всего сигнала строятся диаграммы бикогерентности: по вертикальным и горизонтальным осям откладываются частоты волн в сигнале, а изолиниями обозначаются значения амплитуд бикогерентности. На диаграмме пик на пересечении частот ( f 1 , f 2 ) означает фазовосвязанность волн с частотами f 1 , f 2 и f 3 = f 1 + f 2 .

Экспериментальное оборудование

Исследования проведены в аэродинамической трубе Т-326 Института прикладной механики (ИТПМ) СО РАН. Параметры потока в экспериментах следующие: число Маха набегающего потока М_ю = 5,95; единичное число Рейнольдса Re i, 11,9^10⁶ м^-1 , давление торможения (давление в форкамере трубы) P о = 10⁶ Па и температура торможения T о = 390 К. В ходе экспериментов параметры P о и T о поддерживались постоянными с погрешностью 0,06% и 0,25% соответственно. В качестве модели использовался остроконечный конус длиной 1 м, радиус притупления носика не превышал 0,1 мм. Пульсационные характеристики измерены при помощи термоанемометра постоянного тока (ТПТ). Тестирование гармоническими и прямоугольными импульсами показало, что частотный диапазон используемых в экспериментах ТПТ равняется 400 кГц. Схема эксперимента представлена на рисунке 1.

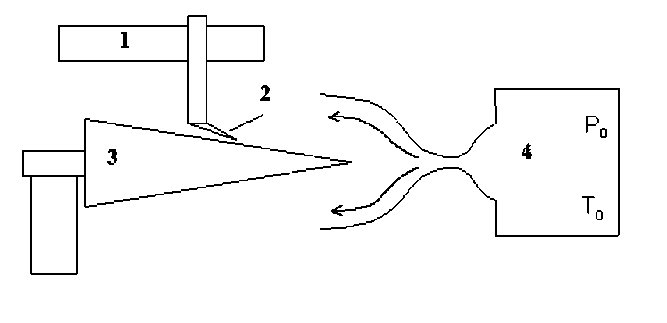
Рисунок 1 - Схема эксперимента: 1 – координатное устройство; 2 – датчик термоанемометра; 3 – модель конуса; 4 – форкамера аэродинамической трубы

Результаты и обсуждение

На рисунке 2 приведены диаграммы бикогерентности для высоты y/S = 0,8 над поверхностью модели, где S - локальная толщина пограничного слоя, соответствующая максимальному уровню значений амплитуд пульсаций. Сверху над диаграммами отображены спектры мощности сигнала пульсаций.

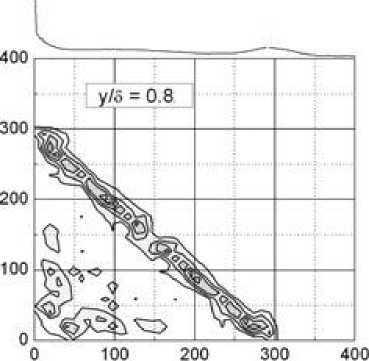
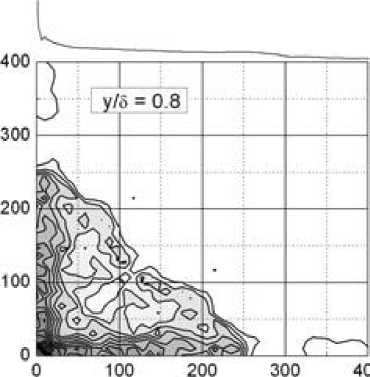
Измерения проведены на расстоянии x = 245 мм от носика модели вдоль образующей конуса (рис. 2 а). Это соответствует параметру, равному корню из числа Рейнольдса R =1970. Как видно, на спектре мощности сигнала наиболее интенсивными являются пульсации на частоте ~ 290 кГц. Максимальные значения амплитуды бикогерентности наблюдаются вдоль линии f 1 + f 2 = 290 кГц до значений bic ² = 0,3. На этой линии основная волна фазово связана со своими субгармониками, что является индикатором субгармонического резонанса. Значения амплитуд в области низких частот f 1 , f 2 < 100 кГц существенно меньше: bic ² <  0,11. Ниже по течению потока ( x = 315 мм и R = 2230, рис. 2 б) на диаграмме бикогерентности наблюдается рост нелинейного взаимодействия в широком диапазоне частот, ограниченных линией субгармонического резонанса. По спектру мощности можно отметить рост амплитуд пульсаций вплоть до 290 кГц, что является следствием перераспределения энергии в спектре. Катализатором данного эффекта является субгармонический резонанс, наблюдавшийся на рисунке 2 а.

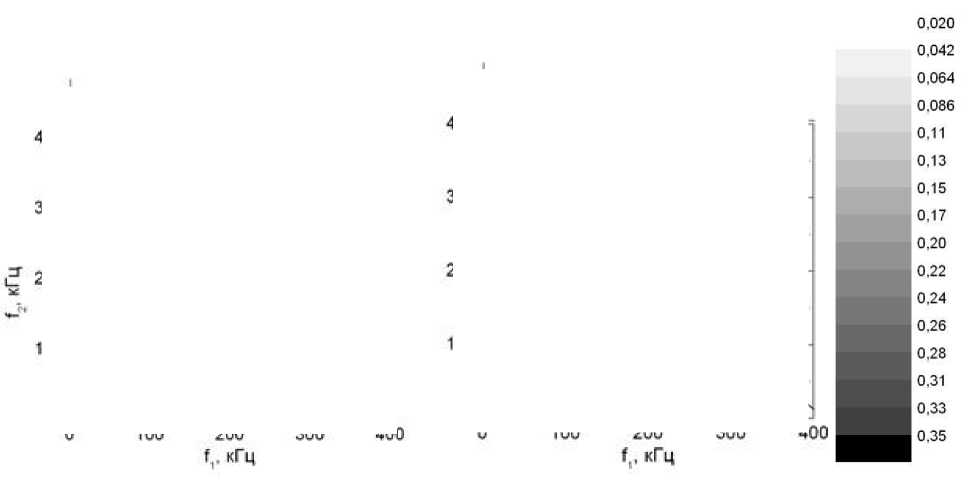
Рисунок 2 - Диаграммы бикогерентности: а - x = 245 мм; б - x = 315 мм

Заключение

Метод спектров высоких порядков позволяет проводить качественный анализ нелинейных взаимодействий между пульсациями различных частот в спектре сигнала. Установлено, что перераспределение энергии в спектре происходит вследствие субгармонического резонанса. Данный метод может быть использован для исследования граничных процессов при взаимодействии потоков плазмообразующего газа и плазменной струи с элементами конструкций в каналах сильноточных газоразрядных устройств различного класса и назначения.