Применение способа интеграции нечётких временных рядов и нечётких онтологий в задачах диагностики технических систем

Неопределённость и неполнота информации – неотъемлемая часть сложных организационно-технических систем, в которых качество функционирования процессов зависит от человека. При анализе, моделировании и проектировании таких систем большое распространение получили экспертные системы, которые используют оценки, основанные на опыте и знаниях эксперта.

Экспертные оценки – это лингвистическая форма какого-либо качественного аспекта оцениваемого элемента системы или самой системы.

Методология логического вывода экспертных оценок на базе предметных онтологий, играющих роль базы знаний в системах поддержки принятия решений (СППР), применяется в различных предметных областях (ПрО), в том числе в области ситуационного управления в энергетике [1], при проектировании сложных диагностических систем [2] и др. Также онтологии нашли применение в качестве базы знаний интеллектуальных систем предупреждения рисковых ситуаций в условиях разнородной информации для этапа проектирования сложных технических систем критической инфраструктуры [3].

Несмотря на широту применения, классические языки онтологии и семантических сетей, которые обычно используются для резюмирования и характеризации особенностей ПрО, не могут быть использованы при раскрытии неопределённости и неточности в знаниях, присущих большинству приложений реального мира в рассматриваемой области.

Нечёткая теория множеств, также как и нечёткая логика – формализмы, подходящие для обработки неполных знаний. Одно из самых эффективных решений представления базы знаний в контексте учёта нечёткости и неопределённости в человеческих рассуждениях и оценках в СППР – представление в виде нечётких онтологий. Так, нечёткие онтологии применяются в таких системах, как: системы диагностики заболеваний [4], нечёткие поисковые системы [5], системы знаний, основанные на групповом принятии решений о важности данных [6] и др. В большинстве случае такие системы оперируют фактами, объектами или терминами, которые описаны естественным языком и содержат особенности рассматриваемой ПрО.

Нечёткие временные ряды (НВР) – это способ получения экспертных оценок, удовлетворяющих условиям полноты, непротиворечивости и адекватности [7]. Одной из основных областей приложений НВР является диагностика процессов. Диагностикой называется процесс, при котором происходит поиск проблем в системе: дефектов, аномалий, неисправностей. При решении задач диагностики сложных технических систем, состояние которых определяется набором данных в виде НВР, целесообразно применять методы сравнения динамики процессов с ожидаемой или требуемой динамикой.

В связи с этим, актуальной задачей, требующей системного решения, является интерпретация полученных результатов анализа в виде экспертных оценок. Для резюмирования результатов, полученных при анализе НВР обычно применяется система правил, которые хранятся в базе знаний экспертной системы. Базой знаний при решении данной задачи выступают онтологии и подобные им графовые формы представления и хранения знаний, которые позволяют учитывать семантические особенности объекта указанной ПрО, а не только их логический вывод [8, 9].

Интерпретирование извлеченных сопоставлений в виде экспертных оценок, значения которых представлены в виде смысловых единиц, которые соответствуют некоторым классам нечёткой онтологии, учитывающих отклонения между текущим и требуемым НВР, могут быть получены при решении задачи интеграции НВР и нечёткой онтологии. Целью данной работы является разработка алгоритмов и моделей интеграции нечётких онтологий и НВР в задачах диагностики сложных технических систем.

1    Нечёткие временные ряды и модель нечёткой онтологии

Модели, а также алгоритмы анализа и прогнозирования НВР подробно описаны в работах [10, 11]. Базовой нотацией представления нечёткой онтологии является стандарт

FuzzyOWL [12-14]. В общем виде любая FuzzyOWL-онтология может быть представлена следующим образом:

• (1)                          I = (I f , C f , P f , A f , D f , Q f , L f , Mod f ),

где

• ■    I f - множество объектов классов онтологии;

• ■    C f - множество нечётких классов онтологии:

• (2)                                C f = { C f^A , C ^Cf } ,

где C_f ^A -множество абстрактных классов, C ^C _f - множество конкретных классов онтологии.

• ■ P f — множество свойств объектов:

• (3)                                P f = { P f^A , P f^C } ,

где P fA множество конкретных свойств, т.е. свойств объектов (ObjectProperty), P fC - множество абстрактных свойств, т.е. свойств типа данных (DatatypeProperty).

• ■ D f — множество аксиом онтологии:

ABox TBox RBox

• (4)                                 D_f = { A_f , A_f , A_f   } ,

где A_f ^ABox – множество утверждений об индивидах, A ^T _f ^Box – множество терминологических аксиом, A_f ^RBox - множество аксиом отношений (иерархия отношений). Часть аксиом может быть подклассом множества нечётких аксиом, которые предполагают истинность утверждения с определённой степенью.

• ■   O f — множество значений степеней, которые могут быть добавлены к объекту нечёт

кой аксиомы:

• (5)                               O f = {LD f , MD f , ND f , Var f },

где LD f – множество лингвистических переменных, MD f – множество степеней модификации, ND f – множество численных значений степеней, Var f – множество переменных.

• ■ L f — множество операторов нечётких логик соответствующих типов: Luk Zad Goed   Pr od

• (6)                                      L_f = { L_f , L_f , L_f , L_f } ,

где L ^L _f ^uk - множество операторов логики Лукасевича, L ^Z _f ^ad - множество операторов логики Заде, L ^G _f ^oed - множество операторов логики Геделя, L ^P _f ^{r od} – множество операторов продукционной логики. Определяются с помощью встроенного отношения hasSemantics .

• ■ Mod f — множество «нечётких модификаторов», т.е. функций модификации функций принадлежности, нечётких классов и нечётких отношений. Функции могут быть линейными или треугольными [15]. В таблице 1 приведены элементы нечётких аксиом FuzzyOWL, а также их возможное представление.

Таблица 1 - Элементы нечётких аксиом в FuzzyOWL

№	Элемент	Возможные значения	Представление в FuzzyOWL
1	LD f – множество лингвистических значений степеней	«рост», «спад», «высокий», «низкий»	#ВысокаяНагрузка datatypeIRI="&rdf;PlainLiteral">fuzzyOwl2 fuzzyType="datatype"; Datatype     type="rightshoulder";      a="15.0"; b="30.0";/fuzzyOwl2
2	MD f – множество степеней модификации	«очень», «быстрый», «медленный»	type="modified" modifier="очень"
3	ND f – множество численных значений степеней	0≤ND≤1	Degree Value=0,6
4	Var f – множество переменных	a, b, c, k1, k2	b="30.0";
5	L f — множество операторов нечётких логик соответствующих типов	Zadeh, Lukasiewicz Goedel and Product	hasSemantics="Zadeh"
6	Mod f — множество нечётких модификаторов	Linear, Triangular

2    Предметная область

Рассмотрим применение подхода интеграции НВР и нечётких онтологий при решении задачи диагностики состояния вертолёта. Диагностика вертолёта заключается в проверке его агрегатов с целью установления их исправности и возможности эксплуатации вертолёта в целом. Результатом проведения диагностики будет оценка значений ключевых показателей физических величин. Основная цель – оценить опасность значений. Для решения этой задачи необходимо построить модели поведения выбранных узлов и с помощью моделей делать заключения об исправности узлов. Модели построены в виде экспертной базы суждений о поведении того или иного компонента. Для построения НВР были определены параметры функций принадлежности (см. таблицу 2).

Таблица 2 - Параметры функции принадлежности

Физический параметр	Границы диапазона	Опасно мало	Мало	Норма	Велико	Опасно велико
Температура  выхлопных газов двигателя, °C	0-1000	a<100 b=200 c=200,5	a=100 b=275 c=350,5	a=350 b=560 c=600,5	a=600 b=700 c=720,5	a=720 b=800 c>1000
Температура масла в двигателе, °C	0-150	a<0 b=5 c=10,5	a=10 b=15 c=20,5	a=20 b=30 c=60,5	a=80 b=100 c=120,5	a=120 b=135 c>150
Давление масла в двигателе, кгс/см 2	0-20	a<0 b=1 c=2,05	a=2,0 b=3,5 c=5,05	a=5,00 b=8 c=10,5	a=10 b=12 c=15,5	a=15,2 b=17,5 c>20
Температура масла главного редуктора, °C	0-100	a<0 b=5 c=10,5	a=10 b=15 c=20,5	a=20 b=35 c=50,5	a=50 b=70 c=80,5	a=80 b=90 c>100
Давление масла главного редуктора, кгс/см 2	0-8	a<0 b=1 c=2,05	a=2,0 b=2,5 c=3,5	a=3,45 b=4 c=4,55	a=4,50 b=5 c=7,55	a=7,5 b=7,8 c>8

Таким образом, для каждой физической величины определено по 5 нечётких меток. Задача анализа технических рядов сводится к задаче поиска аномальных ситуаций в ВР показателей физических величин главного редуктора (ГР) и силовой установки (СУ) двигателя. Анализ представляет собой последовательность следующих шагов:

• 1)    формирование НВР на основе полученной информации о значениях ключевых физических величин после полёта вертолёта;

• 2)    поиск известных аномальных ситуаций в полученных НВР;

• 3)    определение корректности работы узлов. Работа будет считаться некорректной в случае обнаружения хотя бы одной аномальной ситуации.

Для проведения экспериментов была разработана нечёткая онтология. Разработанная FuzzyOWL-онтология имеет иерархическую структуру и включает в себя 55 классов, 8 объектных свойств, 40 типов данных. В ходе выполнения работы были выделены следующие свойства объектов, представленные в таблице 3 (ДМ-давление масла, ГР - главный редуктор, ТВГ – температура выхлопных газов, ТМ-температура масла).

Пример объявления свойства «имеетДМГР»

Таблица 3 - Свойства объектов

Свойство	Домен	Диапазон
имеет ДМ ГР	ГР	ДМ ГР
имеет ДМ левого двигателя	СУ двигателя	ДМ СУ двигателя
имеет ДМ правого двигателя	СУ двигателя	ДМ СУ двигателя
имеет ТВГ левого двигателя	СУ двигателя	ТВГ СУ двигателя
имеет ТВГ правого двигателя	СУ двигателя	ТВГ СУ двигателя
имеет ТМ ГР	ГР	ТМ ГР
имеет ТМ левого двигателя	СУ двигателя	ТМ СУ двигателя
имеет ТМ правого двигателя	СУ двигателя	ТМ СУ двигателя

Помимо этого, было выделено 40 типов данных: по 5 нечётких меток, на 8 вариантов отношений. Параметры типов данных соответствуют параметрам функции принадлежности. Тип функции принадлежности во всех типах данных был выбран треугольный.

Пример объявления типа данных в нотации FuzzyOWL:

#ВеликоДМГР

В качестве объекта экспериментов были исследованы временные ряды для диагностики вертолётных агрегатов и нечёткая онтология конструкции вертолётных агрегатов. В процессе проведения данных экспериментов были использованы алгоритмы интеграции НВР и нечётких онтологии.

3 Эксперименты

Для проверки адекватности алгоритма интеграции НВР и нечёткой онтологии на основе FuzzyOWL, а также корректности работы программного продукта, реализующего данный алгоритм, был проведён ряд экспериментов, в рамках которых были возможные проблемные ситуации. В рамках эксперимента были проведены следующие действия:

Экспертом была разработана нечёткая онтология по стандарту FuzzyOWL. Для построения нечёткой онтологии был использован редактор Protege [16] с подключённым плагином FuzzyOWL Plugin [17]. Фрагмент онтологии представлен на рисунке 1.

Типы данных в нечёткой онтологии FuzzyOWL содержат параметры функций принадлежности, а также привязку к конкретному классу онтологии (Таблица 4).

Задача проведённых экспериментов - это поиск возможных неисправных агрегатов вертолёта. Анализ представляет последовательность следующих шагов:

• 1)    формирование НВР на основе полученной информации о значениях ключевых физических величин после прогона машины;

• 2)    поиск неисправных агрегатов вертолёта в полученных ВР;

• 3)    определение неисправных вертолётных агрегатов.

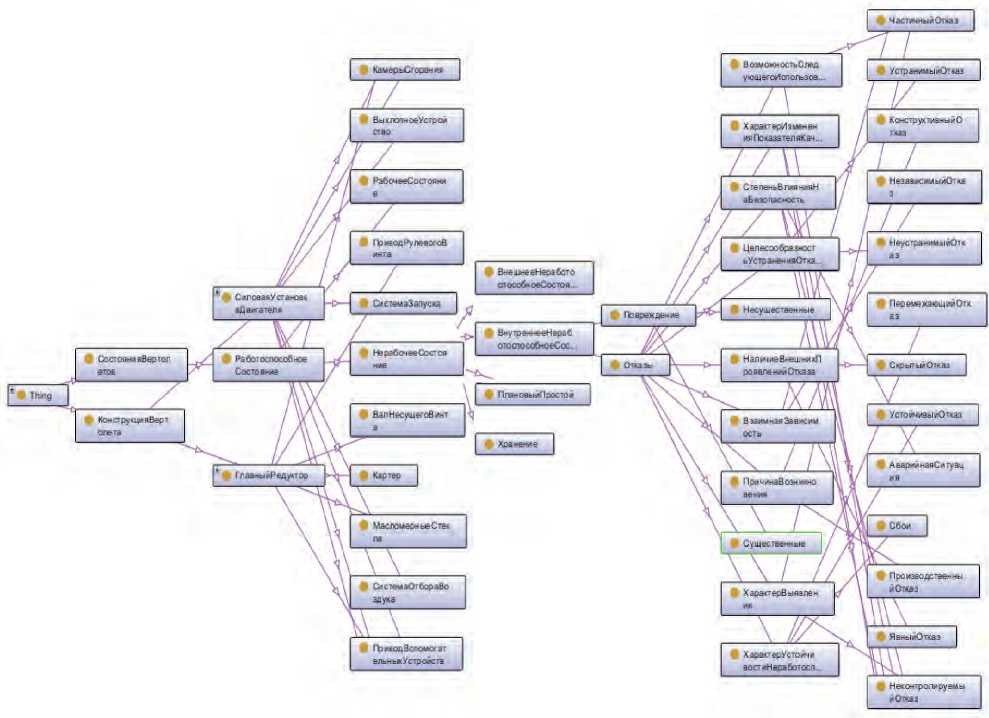
Рисунок 1 – Фрагмент онтологии анализа диагностики основных агрегатов вертолета

Таблица 4 - Таблица описания типов данных

Тип данных	Тип функции принадлежности	Связанный класс	a	b	c
ОпасноМалоТВГЛевДвигателя	треугольная	СУ двигателя	100	200	200,5
МалоТВГЛевДвигателя	треугольная	СУ двигателя	200	275	350,5
НормаТВГЛевДвигателя	треугольная	СУ двигателя	350	560	600,5
ВеликоТВГЛевДвигателя	треугольная	СУ двигателя	600	700	720,5
Опасно ВеликоТВГЛевДвигателя	треугольная	СУ двигателя	720	800	1000
ОпасноМалоДМГлавногоРедуктора	треугольная	ГР	0	1	2,05
МалоДМГлавногоРедуктора	треугольная	ГР	2,0	2,5	3,5
НормаДМГлавногоРедуктора	треугольная	ГР	3,45	4	4,55
ВеликоДМГлавногоРедуктора	треугольная	ГР	4,5	5	7,55
ОпасноВеликоДМГлавногоРедуктора	треугольная	ГР	7,5	7,8	8

Вертолётный агрегат будет считаться неисправным в случае обнаружения хотя бы одной аномальной ситуации для физической величины, привязанной к конкретному классу онтологии, соответствующему данному неисправному агрегату.

Эффективность алгоритма диагностики технических систем может быть оценена при решении задачи моделирования поведения вертолётных агрегатов. Система должна правильно выявлять возможные неисправные вертолётные агрегаты. Для подтверждения эффективности необходимо проанализировать данные, характеризующие машины, как без дефектов, так и с возможными дефектами, после чего проанализировать информацию о не- исправных агрегатах, полученную системой и полученную от эксперта. Для эксперимента были получены данные о прогоне трёх машин, сгенерированы данные, моделирующие те или иные аномальные ситуации. Описание рядов приведено в таблице 5.

Таблица 5 - Описание временных рядов

№ ряда	№ борта	Период	T vg 1	T vg 2	Pm1	Рm2	Pmp	Tm1	Tm2	Tmp
1	210111	15.09.2010	739,59	258,85	2,3	0,8	0	58,1	59,2	29,3
2	210111	16.09.2010	757,29	256,93	2,4	0,8	0	57,1	59	29,3
3	210111	30.09.2010	503	227,78	7,4	0,8	1,8	47,5	51,3	29
4	210111	12.04.2012	536,85	520,93	7,6	6,6	4	53,9	56,5	35
5	240111	11.09.2014	176,43	178	0,8	0,8	0	42,5	46	31,3
6	240111	12.09.2014	176,57	178	0,8	0,8	0	42,5	46	31,3
7	240111	13.11.2016	483	448,85	6,4	5,6	3,4	49,5	51,9	23,5
8	240111	11.08.2017	479,13	0	6,4	5,4	3,3	51,6	55,1	29
9	250111	22.01.2016	189,72	206,22	0,8	1	1,6	52,5	55,5	24,5
10	250111	23.01.2016	193,3	209,22	0,8	1	1,6	52,5	55,5	24,5

Приняты следующие обозначения: T VG 1- температура выхлопных газов левого двигателя, T VG 2- температура выхлопных газов правого двигателя, Pm1 – давление масла левого двигателя, Pm2 – давление масла правого двигателя, Tm1 – температура масла левого двигателя, Tm2 – температура масла правого двигателя, Pmp – давление масла ГР, Tmp – температура масла ГР. Были проведены эксперименты с десятью рядами, результаты которых приведены в таблице 6. Как видно из результатов экспериментов, построение нечёткой онтологии НВР позволило сделать вывод о неисправности агрегата вертолёта при анализе чётких значений показателей агрегатов.

Таблица 6 - Результаты экспериментов

№ борта	Период	T vg 1	T vg 2	Pm1	Рm2	Pmp	Tm1	Tm2	Tmp	Неисправный агрегат
210111	15.09.2010	739,59	258,85	2,3	0,8	0	58,1	59,2	29,3	#СиловаяУстановкаДвигателя
210111	16.09.2010	757,29	256,93	2,4	0,8	0	57,1	59	29,3	#СиловаяУстановкаДвигателя
210111	30.09.2010	503	227,78	7,4	0,8	1,8	47,5	51,3	29	#СиловаяУстановкаДвигателя
210111	12.04.2012	536,85	520,93	7,6	6,6	4	53,9	56,5	35	Неисправных агрегатов нет
240111	11.09.2014	176,43	178	0,8	0,8	0	42,5	46	31,3	#ГлавныйРедуктор
240111	12.09.2014	176,57	178	0,8	0,8	0	42,5	46	31,3	#ГлавныйРедуктор
240111	13.11.2016	483	448,85	6,4	5,6	3,4	49,5	51,9	23,5	Неисправных агрегатов нет
240111	11.08.2017	479,13	0	6,4	5,4	3,3	51,6	55,1	29	#ГлавныйРедуктор
250111	22.01.2016	189,72	206,22	0,8	1	1,6	52,5	55,5	24,5	#СиловаяУстановкаДвигателя
250111	23.01.2016	193,3	209,22	0,8	1	1,6	52,5	55,5	24,5	#ГлавныйРедуктор

Заключение

В работе исследована методика построения нечётких онтологий и разработана онтологическая модель состояния вертолётных агрегатов. Разработан программный продукт, обеспечивающий реализацию интеграции НВР и нечёткой онтологии. Проведены эксперименты по поиску аномальных ситуаций и возможных неисправных агрегатов с использованием разра- ботанного подхода. По итогам проведённых экспериментов можно сделать вывод о том, что предложенный подход интеграции НВР и нечётких онтологий позволяет распознавать аномальные ситуации и находить возможные неисправные агрегаты, соответствующие каждой такой ситуации.

Работа выполнена при финансовой поддержке РФФИ. Проекты № 18-37-00450, № 16-47732070 и 18-47-732007.