Применение структурной модели для расчета усталостной долговечности по корректированной линейной гипотезе суммирования повреждений

Введение. Как показывает анализ, большинство поломок деталей конструкций и машин в процессе эксплуатации происходит вследствие многоциклового усталостного разрушения, вызванного накоплением повреждений под действием переменных нагрузок. В связи с этим при проектировании новых образцов техники большое внимание уделяется прогнозированию ресурса тяжелонагруженных узлов и деталей по критерию усталостной долговечности. Так, например, применительно к транспортным машинам методика расчетной оценки ресурса ходовой системы предполагает моделирование движения машины по трассе в условиях, соответствующих реальной эксплуатации. Полученные в результате интегрирования уравнений движения случайные процессы изменения нагрузок, действующих на исследуемые детали, в дальнейшем преобразуют в процессы изменения напряжений в наиболее нагруженных зонах и получают оценку долговечности с использованием модели накопления усталостного повреждения [1]. При реализации подобной методики наиболее сложным этапом является расчетная оценка усталостной долговечности, что

Расчет и конструирование связано со значительным разбросом характеристик материалов, а также существенным влиянием ряда технологических, конструктивных и эксплуатационных факторов.

В настоящее время для оценки долговечности по критерию многоциклового усталостного разрушения при случайном нагружении находят применение различные подходы. Чаще всего используется методика, предполагающая схематизацию случайного процесса изменения напряжений [2, 3]. При схематизации определяют амплитуды и средние значения напряжения в отдельных циклах, затем строят блок нагружения и с помощью гипотезы суммирования получают оценку накопленного усталостного повреждения [4–6]. Существует также ряд альтернативных подходов. Например, в [7, 8] рассматриваются энергетические методы, в соответствии с которыми мерой накопленного усталостного повреждения является энергия, затраченная на неупругое деформирование. Методика прогнозирования долговечности при случайном нагружении по обобщенной диаграмме усталости предложена в [9]. Кинетическая теория усталости, в соответствии с которой рассматривается снижение предела выносливости по мере накопления повреждений, рассматривается в [10]. Использованию марковских процессов для описания накопления повреждений посвящена работа [11]. Перечисленные методики предназначены в основном для оценки усталостной долговечности при простых видах нагружения. В случае однопараметрического нагружения при сложном напряженном состоянии, когда компоненты тензора напряжений изменяются во времени синхронно и пропорционально, рекомендуется выполнять расчет эквивалентных амплитуд напряжений и далее проводить расчет как при одноосном нагружении [12].

Наиболее сложным является случай многопараметрического случайного нагружения, при котором в опасной зоне детали случайные процессы изменения компонентов тензора напряжений являются независимыми. В подобных условиях работают рамы и несущие корпуса транспортных средств, а также некоторые детали ходовых систем [1]. Анализ литературных источников показывает, что для такого вида нагружения стандартные методики расчетной оценки усталостной долговечности отсутствуют. В связи с этим большой интерес представляет разработанная на кафедре прикладной механики, динамики и прочности машин ЮУрГУ группой исследователей под руководством профессора О.С. Садакова модель накопления повреждений, базирующаяся на использовании структурной модели среды [13, 14]. Такой подход, первоначально разработанный для случая малоцикловой усталости, позволяет получать оценки долговечности как при однопараметрическом, так и при многопараметрическом нагружении. В [15] предложено распространить его на случай многопараметрического многоциклового нагружения. Данная статья посвящена дальнейшему развитию этого подхода, связанному с использованием корректированной линейной гипотезы накопления повреждений.

Модель накопления повреждений. Приращение накопленного повреждения определяется выражением:

d ω= K ⋅ν^β⋅ d λ ,                                                                         (1)

d λ= Δ p _k I) .                                                                                     (2)

Значение v на каждом шаге нагружения является функцией числа сместившихся поверхностей текучести n .

Представленный метод позволяет рассчитать накопленное повреждение для любой траектории движения точки e , в том числе и для случая многопараметрического нагружения. В работе [15] его предложено распространить на случай многоцикловой усталости. Это оказывается возможным, поскольку на диаграмме Велера области много- и малоциклового разрушения являются различными участками одной кривой. Вместо пластических деформаций в этом случае рассматривают микропластические деформации, вызывающие накопление повреждений при практически упругой работе материала. Для их расчета можно использовать описание диаграммы деформирования зависимостью Рамбер - Осгуда [17]:

r = A ■ P m ,                                                                                        (3)

где r и p - интенсивность упругой и пластической деформации, A и m - постоянные (характеристики материала). Методика определения A и m по пределу текучести и пределу прочности материала представлена в [18]. Сопоставление расчетных и экспериментальных диаграмм деформирования для различных сталей и сплавов показывает, что погрешность обычно не превышает 5 %.

Идентификацию модели накопления повреждений (определение констант K и в ) обычно осуществляют, приравнивая повреждения, рассчитанные в соответствии с (1) и по формуле Коффина:

N f ■A p ^а = C ,                                                                           (4)

где а и С - постоянные, N - число циклов до разрушения, A p - интенсивность размаха пластической деформации в цикле. Для получения адекватных результатов в случае многоцикловой усталости параметры а и С следует определять на основе диаграммы Велера, связывающей амплитуду напряжений c a с числом циклов до разрушения при симметричном цикле нагружения:

NT = (~) m

N 0 о a где о-1 - предел выносливости детали, N0 - базовое число циклов, mv - показатель наклона. Приравнивая значения Nf, полученные по (4) и (5), можно определить значения параметров а и С:

N_f = C ■A p ^-а = C ( ^' G ■ A ) ^{а / m} = N ( ° -- ) m v , C = N ( 2 ° ) m v , а = m ■ m_v .             (6)

f                  2 o a              о a           ^u 76 ■ G ■ A

Значения параметров модели (1) K и в получают в результате приравнивания повреждения за симметричный цикл при одноосном нагружении:

1     An^{a      A} p         ^A p

Am =---=----= 2 ■ j d to =2 ■ j K ■ v^e dp .

Nf   ^C     0       0

В качестве исходных данных при расчете накопленного повреждения используются массивы значений компонентов тензора напряжений, заданных с постоянным шагом по времени A t . Используя известные соотношения, из компонентов тензора напряжений получают значения компонентов девиатора деформаций. Поскольку при напряжениях, характерных для многоцикловой усталости, материал работает практически линейно, на этом этапе используются соотношения теории упругости. Затем для каждого шага нагружения в девиаторном пространстве определяют смещение центров поверхностей текучести и определяют v i , AX i . Приращение накопленного повреждения на I- м шаге нагружения определяется выражением:

Am i = K ■v i ^e-AX i . (8)

Общее накопленное повреждение to получают в соответствии с линейной гипотезой суммированием Ac^ на каждом шаге; условие m = 1 служит критерием разрушения (возникновения усталостной трещины):

^m = E ^Am i = ^L (9) l

Результаты проверки адекватности модели приведены в [15]. На первом этапе была выполнена серия расчетов для случая циклического растяжения - сжатия (однопараметрическое нагружение). Рассматривалось гармоническое, бигармоническое (с различным соотношением частот и амплитуд составляющих) и случайное нагружение. Результаты расчета усталостной долговечно-

Расчет и конструирование сти по предлагаемой модели сопоставлялись с результатами, полученными традиционным методом, предусматривающим схематизацию процесса изменения напряжений методом «дождя» [19, 20] и последующий расчет накопленного повреждения с помощью линейной гипотезы суммирования. Отличие результатов не превышает 20 %, что является вполне приемлемым для оценки усталостной долговечности. В качестве примера на рис. 1 представлены фрагменты процессов изменения напряжений и сопоставление результатов расчетов для бигармонического и случайного нагружения (Lsm – долговечность, рассчитанная по предлагаемой методике с использованием структурной модели материала, Lrf – результат, полученный при схематизации процесса методом «дождя»). На следующем этапе было проведено сопоставление результатов расчета с экспериментальными данными при двухпараметрическом нагружении (плоское напряженное состояние), которое также продемонстрировало хорошее соответствие.

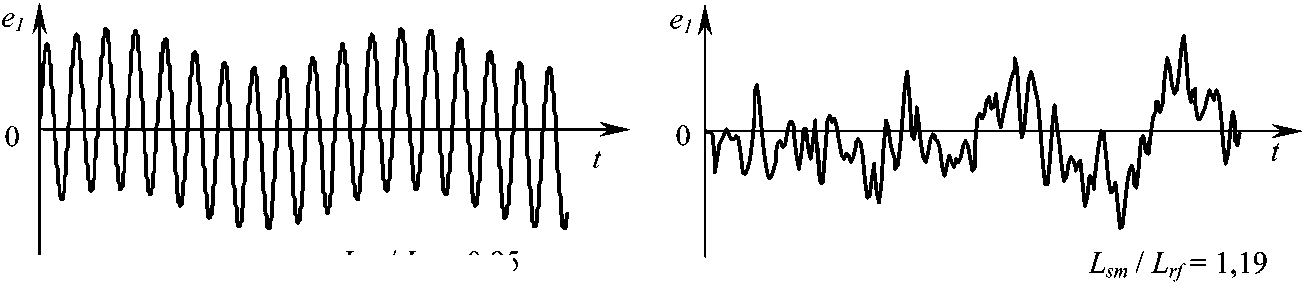
L_Sm / L^ 0,95

Рис. 1. Процессы нагружения и сопоставление результатов тестовых расчетов

Одним из недостатков предложенного подхода является использование линейной гипотезы суммирования повреждений. Сопоставление экспериментальных данных с результатами расчетов показывает, что в этом случае расчетная оценка усталостной долговечности часто оказывается завышенной. В связи с этим в настоящее время чаще используется корректированная линейная гипотеза [3]. Традиционная методика оценки усталостной долговечности при простых видах нагружения предусматривает схематизацию случайного процесса методом «дождя» или полных циклов и формирование блока нагружения, в котором каждому дискретному значению амплитуд напряжений σ ai ставится в соответствие число циклов η i , которые деталь нарабатывает в течение одного часа работы изделия на i- м уровне. В соответствии с корректированной линейной гипотезой суммирования повреждений разрушению (зарождению усталостной трещины) соответствует выполнение условия:

M

T⋅∑ηiσamiv i=1 N0σ-m1v ap,

где T – продолжительность работы в часах, a p – корректирующий коэффициент, зависящий от формы блока нагружения. Значение a p определяют по эмпирическим зависимостям:

M

∑σaiηi ap=(ξ⋅σamax/σ-1-0,5)/(σamax/σ-1-0,5), ξ=i=1       ,                                (11)

σamaxηbl где ηbl – общая продолжительность блока, σamax – максимальная амплитуда напряжений в блоке. Если значение ap , полученное по этим выражениям, оказывается меньше 0,1, в расчетах принимается ap = 0,1.

По аналогии для использования корректированной линейной гипотезы в модели накопления повреждений, основанной на структурной модели среды, в выражении (9) необходимо заменить единицу на a p :

ω= ∑ Δω l = a p .                                                              (12)

l

Однако в этом случае расчет накопленного повреждения производится непрерывно, на каждом шаге, без построения блока нагружения, необходимого для расчета ap. Как показывает анализ, при однопараметрическом нагружении использование структурной модели позволяет выделить отдельные циклы из случайного процесса изменения напряжений путем подсчета числа ре- версов в перемещениях каждой поверхности текучести. В дальнейшем это позволяет построить блок нагружения и определить значение ap. Возможность такого подхода иллюстрирует рис. 2.

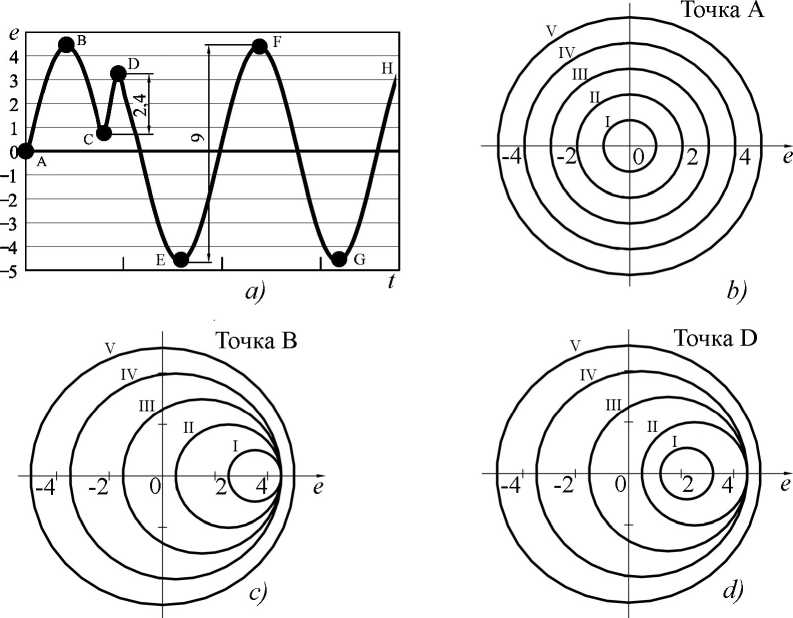
Рис. 2. Процесс нагружения и перемещения поверхностей текучести

На рисунке схематично изображен процесс изменения во времени одной из компонент девиатора напряжений ( e ) и плоскость в девиаторном пространстве, на которой поверхности текучести изображены в виде окружностей. Процесс изменения e ( t ) включает два цикла с амплитудой 4,5 и один цикл с амплитудой 1,2 (в условных единицах), которые, очевидно, могут быть выделены из него при обработке методом «дождя» или полных циклов. Поверхности текучести I–V имеют радиусы R k , равные 1, 2, 3, 4 и 5 (в условных единицах). В начальный момент времени (точка А ) центры поверхностей текучести совпадают с началом координат. Поверхность V, имеющая радиус, превышающий наибольшее значение e ( t ), в процессе нагружения будет оставаться неподвижной. В точке В траектории нагружения поверхности I–IV переместятся в крайнее положение. При движении от точки А до F поверхности II–IV два раза изменят направление движения, а поверхность I совершит еще два дополнительных реверса на участке B – C – D – E . Общее число реверсов Nr k для каждой из поверхностей на рассматриваемой траектории (A – H) приведено в табл. 1. Значения Nrb k получают по следующей формуле:

Nrb k = Nr k – Nr k+1 , k = 1 … Km – 1; (13) где Km – общее число поверхностей текучести (в данном примере Km = 5). Указанные значения для рассматриваемого примера также приведены в табл. 1. Для поверхности IV Nrb 4 = 4, что соответствует числу полуциклов с амплитудой, находящейся в диапазоне 4 … 5; в данном примере это два цикла с амплитудой 4,5. Для поверхности I Nrb 1 = 2, что соответствует числу полуциклов с амплитудой, находящейся в диапазоне 1 … 2 (в данном примере – цикл с амплитудой 1,2).

Таким образом, если при расчете с помощью структурной модели материала подсчитывать число реверсов при перемещении каждой поверхности текучести, а потом обработать результаты в соответствии с (13), можно получить информацию о числе циклов различной амплитуды, присутствующих в случайном процессе. В дальнейшем на ее основе можно построить блок нагружения, необходимый для расчета корректирующего коэффициента a p .

Таблица 1

Число реверсов поверхностей текучести

№ поверхности ( k )	1	2	3	4	5
R k	1	2	3	4	5
Nr k	6	4	4	4	0
Nrb k	2	0	0	4	—

Расчет и конструирование

Результаты расчетов. Для проверки предложенной методики была выполнена серия расчетов, при которых проводилась обработка случайных процессов методом «дождя» и с помощью структурной модели. По результатам расчетов строились блоки нагружения и определялись значения a p . В качестве примера рассмотрим результаты, полученные для трех различных случайных процессов изменения напряжений. На рис. 3 представлены фрагменты этих процессов и соответствующие блоки нагружения. Процессы изменения напряжений различаются спектральным составом и формой блоков нагружения. Процесс № 1 – узкополосный, в блоке нагружения преобладают циклы с максимальной амплитудой; процесс № 3 – широкополосный, с преобладанием составляющих малой амплитуды. Коэффициенты сложности структуры процессов ( β ), числовые характеристики блоков нагружения, а также значения ξ и a p , полученные двумя методами, приведены в табл. 2.

Рис. 3. Случайные процессы и блоки нагружения

Анализ представленных данных показывает, что блоки нагружения, построенные двумя рассматриваемыми методами, отличаются незначительно; значения корректирующих коэффициентов a p отличаются не более чем на 15 %. Различие результатов прогнозирования долговечности также не превышает 15–20 %.

Таблица 2

Параметры блоков нагружения

σ ai / σ a max	Процесс № 1, β 1 = 0,93		Процесс № 2, β 2 = 0,80		Процесс № 3, β 3 = 0,61
	η i / η bl		η i / η bl		η i / η bl
	метод «дождя» ξ = 0,70 ap = 0,59	структурная модель ξ = 0,68 ap = 0,56	метод «дождя» ξ = 0,38 ap = 0,14	структурная модель ξ = 0,40 ap = 0,16	метод «дождя» ξ = 0,29 ap = 0,10	структурная модель ξ = 0,29 ap = 0,10
0,0–0,1	0,049	0,048	0,167	0,160	0,262	0,243
0,1–0,2	0,025	0,023	0,067	0,067	0,238	0,242
0,2–0,3	0,027	0,027	0,133	0,134	0,123	0,127
0,3–0,4	0,009	0,009	0,233	0,252	0,085	0,087
0,4–0,5	0,038	0,039	0,067	0,067	0,131	0,135
0,5–0,6	0,078	0,079	0,067	0,084	0,077	0,080
0,6–0,7	0,184	0,185	0,167	0,134	0,023	0,024
0,7–0,8	0,332	0,338	0,067	0,067	0,031	0,032
0,8–0,9	0,224	0,222	0,000	0,000	0,023	0,024
0,9–1,0	0,031	0,031	0,000	0,034	0,008	0,008

Заключение. В статье рассмотрена методика прогнозирования долговечности при многоцикловом случайном нагружении, основанная на применении структурной модели материала. Для повышения точности результатов расчетной оценки предложено использовать корректированную линейную гипотезу суммирования повреждений. Показано, что в случае однопараметрического случайного нагружения применение такого подхода дает результаты, хорошо согласующиеся с традиционными методами. Отличие в оценке ресурса не превышает 15–20 %. С учетом большого естественного разброса характеристик материалов такой результат является вполне допустимым.

В рамках разработанной методики предложен алгоритм определения числа циклов различной амплитуды, составляющих случайный процесс. Алгоритм основан на анализе числа реверсов при перемещении поверхностей текучести структурной модели. Он может представлять самостоятельный интерес при разработке методов схематизации случайных процессов.