Применение субъективных вероятностей, критерия ожидаемой полезности и вероятностно-теоретических моделей с тяжелыми хвостами в управлении социально-экономическими объектами

Интерес к субъективной теории вероятностей (ТВ) как к области научного знания появился в 30-е годы ХХ века. До сих пор эта область является малоизученной и дискуссионной. Субъективная вероятность (СБВ) по своей сути близка к методам принятия решений в условиях неопределенности, поскольку эксперт, который проводит оценки, базируется на своем личном опыте и знаниях, поэтому оценки одного и того же события разными экспертами могут существенно отличаться друг от друга.

В статье рассматриваются виды СБВ, методы ее получения, функционал ожидаемой полезности (ФОП), а также их применение на практике для нахождения наиболее выгодного (квазиоптималь-ного) сценария тестирования программного модуля в составе выполняемого проекта; представлено исследование имеющихся дефектов на проекте при использовании одного из сценариев и приведено его описание в виде модели с «тяжелым хвостом».

Методы определения СБВ

Решения, которые принимаются в условиях неопределенности, каждый день пронизывают жизнь любого человека и организации. Достаточно часто встречаются случаи, когда мы не имеем представление о вероятностях состояний природы. Все, что мы знаем – это перечень вариантов состояний, оценить которые в полной мере мы не можем.

В таких случаях вероятности состояния природы могут быть оценены субъективно. Поэтому большое значение приобретает оценка СБВ осуществления того или иного сценария развития прогнозируемого объекта. Теория СБВ – это теория вероятностей, изучающая оценки человеком достоверности уникальных событий [1]. Другими словами, СБВ представляет собой шанс, который приписывается событию конкретным человеком. Другой человек может иначе оценивать шансы этого события. Оценки СБВ различных событий, как правило, основываются на личном опыте, общественном мнении и анализе конкретной ситуации. Особенно полезна СБВ в ситуациях, когда эмпирическую вероятность события вычислить невозможно.

В зависимости от формы представления СБВ можно разделить на качественную и количественную. Существует много методов, нацеленных на количественную оценку СБВ, но стоит отметить, что практически во всех методах для получения оценки используют опрос эксперта (группы экспертов). Поэтому целесообразно для принятия решения использовать уже формализованные методы. Методы получения количественной СБВ можно поделить на две группы: методы с конечным множеством событий, которые нацелены на оценку вероятно- сти каждого события в отдельности (метод прямой оценки вероятности событий, метод отношений, метод собственного значения, формула Байеса) [2] и методы с бесконечным множеством событий (метод переменного интервала, метод фиксированного интервала, графический метод) [3-4].

Для качественной СБВ выбирается преимущественный, то есть наиболее вероятный объект: это может быть предположительное развитие события (явления) или наиболее вероятный исход принятого решения. Такая вероятность считается более надежной, чем и отличается от количественной вероятности, когда объекту проставляются экспертами оценки. К методам получения качественной СБВ можно отнести экспертные методы (Дельфи, разработки сценариев, морфологический анализ) [5].

Чтобы выделить и идентифицировать существенные факторы риска, повысить эффективность процесса управления исследуемым объектом, получить возможность принятия правильного решения, необходимо дополнение СБВ с помощью количественного анализа. Поэтому результаты качественного анализа служат важной исходной информацией для дальнейшего получения количественной СБВ, которая предусматривает ее вычисление.

Функционал ожидаемой полезности (ФОП) в рамках теории субъективной ожидаемой полезности можно использовать для исследования и анализа процессов принятия решений в сложных системах. Рассмотрим ситуацию, когда лицу, принимающему решение (ЛПР) необходимо оценить i -й сценарий развития событий. Тогда для получения критерия эффективности сценария может быть использована следующая формула [6]:

Q_i=P_i(P_FF_i-P_cG_i), (1)

где F_i – позитивный эффект, прогнозируемый ЛПР ; G_i – затраты на ресурсы; Р_F – вероятность получения прибыли; Р_G – вероятность получения ресурсов; Р_i – вероятность разрешения реализации проекта; i – номер сценария.

Применение СБВ и ФОП на практике

Рассмотрим применение различных методов СБВ на примере оценки тестирования одного из новых модулей проекта. Перед руководством поставлена задача: провести качественное полное тестирование модуля с покрытием всех возможных кейсов . Для решения такой задачи нужно правильно подобрать ресурсы и выбрать наилучший способ тестирования, чтобы обеспечить прибыль для компании.

Первый этап. Необходимо определить варианты действий ЛПР, то есть сценарии развития событий. Для такой задачи хорошо подходит метод сценариев (см. таблицу 1).

Второй этап. Получить вероятности затрат, прибыли, привлекательности по каждому сценарию, используя методы количественной субъективной вероятности с конечным множеством.

Используем формулу Байеса, так как эксперту с ее помощью легче провести оценку – не оценивая отношение вероятностей друг к другу, а просто проставив по шкале оценки событий. Такой подход более прост при восприятии ситуации человеком. В нашем случае экспертом была проведена оценка по затратам для трех сценариев: P ( G ₁) = 4, P ( G ₂) = 5, P ( G ₃) = 2, P ( A_G | G ₁) = 7, P ( A_G | G ₂) = 6, P ( A_G | G ₃) = 9. На основе этих значений был вычислен нормирующий параметр P ( A_G ) = 76, соответствующий полной вероятности в формуле Байеса. Расчет апостериорных вероятностей затрат дает Р_{G 1} = 0,37; Р_{G 2} = 0,39; Р_{G 3} = 0,24.

Аналогичным образом были получены вероятности прибыли и привлекательности для каждого сценария: Р_{F 1} = 0,33; Р_{F 2} = 0,14; Р_{F 3} = 0,53 и Р ₁ = 0,34; Р ₂ = 0,13; Р ₃ = 0,53.

Третий этап. Рассчитать ФОП для рассматриваемых сценариев на основе полученных СБВ и выявить наилучший вариант. Для получения критерия эффективности сценария используем формулу (1). Подставив найденные значения СБВ получим Q ₁ = 0,099; Q ₂ = –0,014; Q ₃ = 0,435.

Определим наиболее эффективный вариант развития событий путем максимизации критерия Q_i . Таким образом, получается, что наиболее оптимальным является сценарий 3.

Проведем анализ найденных дефектов при использовании сценария 3 (длительность тестирования составляет 75 рабочих дней, то есть 1800 рабочих часов). За указанный интервал времени было обнаружено 220 дефектов.

Определим число групп, которые будут описывать имеющуюся выборку, по формуле Стерджесса [7]:

n = 1 + 3,322 lg?V = 1 + 3,3221g 1800 = 11,813; (2)

где n – число групп; N – число единиц совокупности (в нашем случае – временных интервалов). С округлением в меньшую сторону принимаем n = 11, то есть выборка будет включать 11 интервалов. Определим шаг интервала h [8]:

_{/? =} К^^1 = (1800-0) _{= 164}

n            11

Таблица 1. Основные сценарии процесса тестирования модуля проекта

	Сценарий 1	Сценарий 2	Сценарий 3
Способ тестирования	Тестирование осуществляется за счет существующих ресурсов проекта. Вид тестирования: комбинированное (ручное и автоматизированное).	Полностью ручное тестирование. Есть потребность в найме новых сотрудников.	Тестирование осуществляется с помощью автотестов с незначительной долей ручного тестирования. Привлечение дополнительных сотрудников.
Ресурсы	1    QA Analyst осуществляет анализ тестирования и информационную поддержку (ставка на проекте в день: 0,5); 2    QA способны подготовить пререквизиты для автотестов, написание автотестов (знания базовые), провести ручное тестирование, написание документации (ставка на проекте в день: 1).	1    QA Analyst осуществляет анализ тестирования и информационную поддержку, обучение новых QA (ставка на проекте в день: 0,75); 2    QA осуществляют ручное тестирование, написание документации (ставка на проекте в день: 1); 2    Junior QA осуществляют ручное тестирование несложных задач.	1    QA Analyst осуществляет анализ тестирования и информационную поддержку QA и ТА (ставка на проекте: 0,5); 2    QA осуществляют подготовку пререквизитов для автотестов, запуск и наладку автотестов, ручное тестирование непокрытых кейсов автотестами, написание документации (ставка на проекте: 1); 1 ТА осуществляет написание автотестов (ставка на проекте: 1).
Задействование ресурсов в течение всего времени тестирования	Полное	Полное	1 QA Analyst - 0,75 1 QA-0,75 1 QA - 1 1 ТА - 0,5
Время тестирования (рабочих дней)	120	90	75

Таблица 2. Группировка выявленных дефектов по интервалам

Интервал Диапазон, часы Частота,/ Накопленная частота, сумма/ 1 0-164 7 7 2 164-328 3 10 3 328 - 492 2 12 4 492 - 656 27 39 5 656-820 45 84 6 820 - 984 51 135 7 984- 1148 43 178 8 1148-1312 27 205 9 1312-1476 4 209 10 1476- 1640 3 212 И 1640- 1800 8 220 где xmax – максимальное значение признака в совокупности; xmin – минимальное значение признака в совокупности. Проведем группировку имеющихся значений с равными интервалами, представленными в таблице 2, для построения гистограммы.

Данная выборка соответствует условию нормировки:

J p{x}dx = 1, (4)

где р ( x ) – плотность распределения вероятности (ПРВ) рассматриваемой случайной величины х . На рисунке 1 показаны экспериментальная гистограмма и два варианта ее аппроксимации: нормальный закон (штриховая линия) и распределение, учитывающее «тяжелый хвост» гистограммы (сплошная линия). Распределения с «тяжелыми хвостами» – это такие распределения, для которых вероятность случайной величины отклониться от средних значений будет значительно выше, чем, например, для нормального распределения. Наличие «тяжелых хвостов» у ПРВ случайной величины х существенно затрудняет ее компьютерное моделирование. Хвосты у ПРВ обычно появляются в результате обработки экспериментальных гистограмм, когда выясняется, что полученные данные хорошо соответствуют нормальному закону лишь в центральной части области распределения х [9].

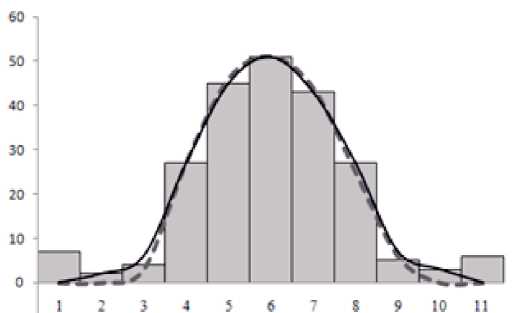
Рисунок 1. Симметричная ПРВ с «тяжелыми хвостами»

Распределения с «тяжелыми хвостами» встречаются в таких областях, как страхование, финансовая деятельность, экономические и компьютерные исследования, телекоммуникации, лингвистика, экономика, социология, биология и т.д.[10].

Заключение

В статье рассмотрено применение субъективной теории вероятностей, методов получения СБВ и ФОП на практике для выявления наилучшего (квазиоптимального) сценария тестирования программного модуля на проекте. Также был проведен анализ выявленных дефектов по результатам использования наилучшего сценария и приведено его описание в виде модели с «тяжелыми хвостами».