Применение технологии проектирования интеллектуальных систем управления на основе мягких вычислений (на примере перевернутого маятника)

В данной работе рассматривается способ повышения надежности и адаптивности систем автоматического управления (САУ) с помощью специального программного инструментария – оптимизатора баз знаний (ОБЗ) на мягких вычислениях [1]. Использование ОБЗ позволяет уменьшить время проектирования интеллектуальной системы управления (ИСУ), повысить робастность и устранить субъективизм при формировании БЗ нечеткого регулятора (НР). Управление неустойчивым динамическим объектом типа «каретка – перевернутый маятник» является одной из типовых задач в теории управления, так как ее решение наглядно демонстрирует качество САУ. Задача управления состоит в том, чтобы, воздействуя с помощью силы управления на тележку, удерживать маятник в вертикальном положении (угол отклонения оси маятника от вертикали близок к 0) в условиях непредвиденно-гоизменения условий среды функционирования.

Такая задача часто решается с использованием традиционной САУ на основе пропорционально-интегрально-дифференциального регулятора (ПИД-регулятора) в контуре управления [2, 3]. Если коэффициенты усиления регулятора являются постоянными величинами, то система управления не обеспечивает достаточной робастности. В этом случае система неспособна функционировать в нештатных и непредвиденных ситуациях и демонстрирует недостаточную эффективность управления [1]. Обычно настройка регуляторов сопровождается большим количеством экспериментов и множеством осложнений, связанных с неопределенностью некоторых параметров системы, наличием помех в каналах измерения и системе управления. Во многих работах отражена возможность использования различных интеллектуальных методов – нейронных сетей [4] и генетических алгоритмов [5, 6].

В данной работе отражены особенности применения нечетких регуляторов в контуре управления в реальном времени.

Оптимизатор баз знаний

Применительно к проектированию ИСУ, мягкие вычисления представляют собой комбинацию из следующих подходов: теория нечетких системы, генетические алгоритмы (ГА) и нечеткие нейронные сети (ННС).

НР является центральным элементом ИСУ и вырабатывает управляющие сигналы изменения во времени (законы управления) коэффициентами усиления ( k , k_d , k_i ) ПИД-регулятора. Ядро НР основано на процессе проектирования БЗ, которая интегрирована в интеллектуальный контроллер. Структурно БЗ состоит из продукционных логических правил, которые включают нечеткие входные и выходные значения функции принадлежности лингвистических переменных.

Функциональная структура ИСУ с блоками НР и ОБЗ на мягких вычислениях представлена на рис. 1.

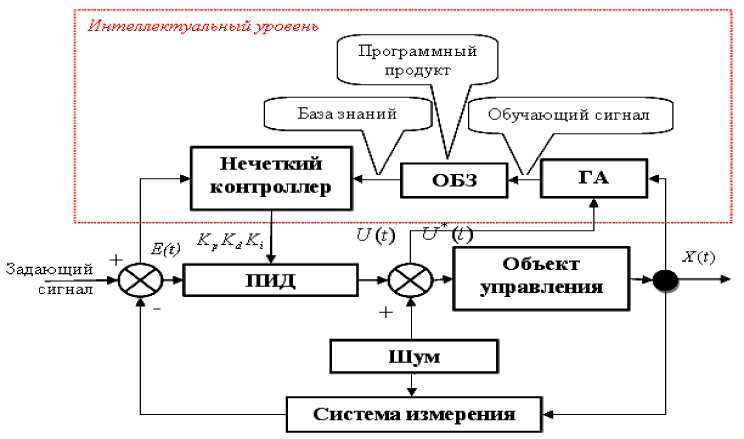
Рис. 1. Структура ИСУ с нечетким регулятором и оптимизатором баз знаний

Такая структура включает одновременно следующие качества управления: управляемость, точность и устойчивость (нижний уровень управления – САУ) и обучение и адаптация (верхний интеллектуальный уровень управления – НР с БЗ).

Наиболее актуальной проблемой при создании ИСУ является получение оптимальной и робастной БЗ, которая гарантирует достижение требуемого уровня качества управления. При проектировании БЗ возникают трудности, связанные со сложностью динамической системы и наличием шумов в системе измерения и управления.

В данной работе рассматривается возможность подключения реального удаленного ОУ для настройки БЗ в НР в режиме реального времени на основе ОБЗ.

Входом ОБЗ является обучающий сигнал (ОС), который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т.е. непосредственно из результатов измерений динамических параметров физической модели ОУ.

ОС является источником знаний и представляет собой массив данных, разделенный на входные и выходные составляющие, каждая из которых, в свою очередь, состоит из одного и более сигналов. В общем виде, каждый из составляющих сигналов является выборочной (репрезентативной) траекторией некоторого случайного процесса. При этом подразумевается, что в каждый момент времени существует некоторая корреляция между входными и выходными сигналами. Например, в случае аппроксимации некоторого управляющего сигнала, входными компонентами могут являться ошибка управления, интеграл ошибки и ее производная, а выходным компонентом – требуемое значение управляющего воздействия, либо некоторые настраиваемые параметры системы управления, например коэффициенты усиления ПИД-регулятора.

На рис. 2, входными данными для НР является вектор ошибки, который состоит из ошибки .     e(t )                  к          . ^ie = ed^dt   .___ .

управления    , интеграла ошибки управления         и скорости изменения ошибки управления

e(t) . Выходными данными НР является вектор, состоящий из значений коэффициентов усиления pp , kk d , i ПИД – регулятора, значения которых применяются в формировании управляющего воздействия в виде:

е -0. 01 -0. 02 -0. 04 -0.05	ё -0. 01 -0. 01 -0. 01 -0. 01	| edt "г -0. 01 -0. 04 -0. 07 -0. 12	кр 13. 38 13. 38 13. 38 13. 38	к 0.48 0.48 0.48 0.48	к= 20. 13 20. 13 20. 13 20. 13
0.25	-0. 02	7. 67	14. 20	0. 30	16. 26
0. 18	-0. 07	7. 84	14. 20	0. 30	16. 26

Рис. 2. Обучающий сигнал

Структурно ОБЗ состоит из взаимосвязанных генетических алгоритмов (ГА1, ГА2, ГА3), оптимизирующих отдельные компоненты БЗ [1]. Базовые шаги оптимизации и структура ОБЗ представлены на рис. 3.

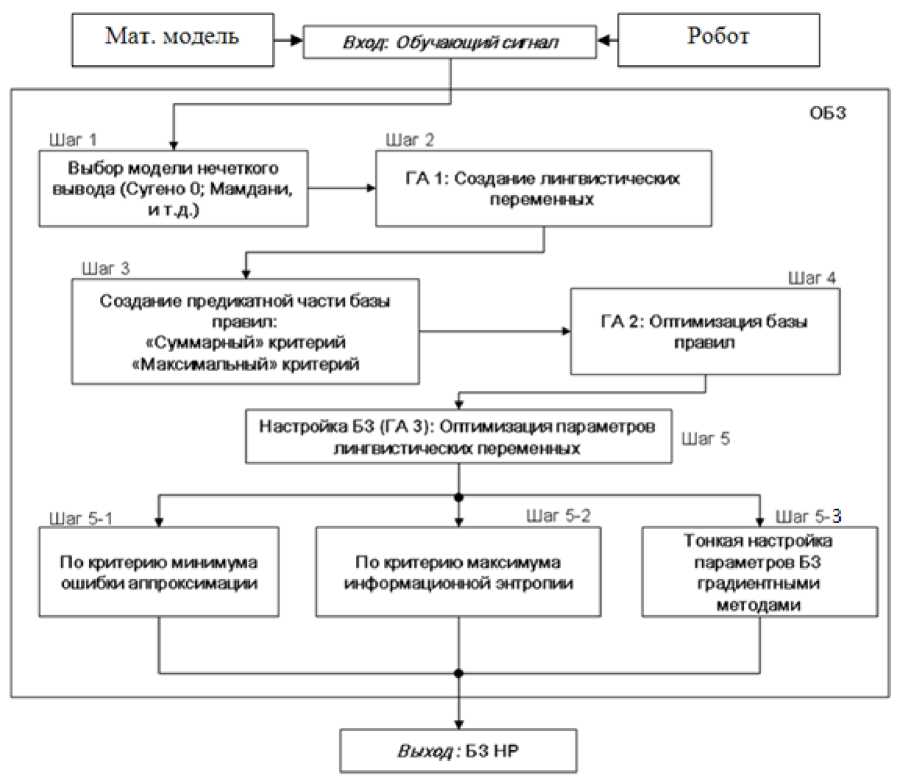
Рис. 3. Структура ОБЗ и шаги оптимизации

Результатом аппроксимации ОС является построенная БЗ для НР, включающая оптимальное конечное множество правил и оптимально сформированные параметры функции принадлежности входных и выходных переменных НР.

Таким образом, результатом проектирования является требуемый тип универсального аппроксиматора в виде НР с оптимальной структурой БЗ.

Одним из интерфейсов взаимодействия с ОБЗ является интерфейс дистанционной настройки. Рассмотрим технологию дистанционного проектирования робастных ИСУ (на основе удаленного соединения с ОУ) для настройки БЗ нечеткого регулятора (НР) на основе ОБЗ с применением технологии мягких вычислений [12]. Такая возможность позволяет проектировать ИСУ без использования системы стохастического моделирования, что дает преимущество при проектировании нечетких систем управления для сложных и слабо формализованных ОУ в непредвиденных ситуациях управления.

Кроме того, дистанционная настройка БЗ дает возможность максимально адаптировать нечеткую систему управления для конкретной (непредвиденной) ситуации управления независимоот времени и места нахождения ОУ. Такого рода самоорганизующиеся ИСУ с дистанционным проектированием БЗ важны для ликвидации последствий аварий на АЭС, при разборе завалов при землетрясениях, крушении поездов, для работы в загрязненной и радиоактивной окружающей среде и т.п.

Рассмотрим возможность удаленной настройки БЗ для реального ОУ [12].

Удаленная оптимизация БЗ осуществляется на четвертом этапе проектирования НР. Реализация физической среды соединения предполагает использовать дополнительное оборудование для приема – передачи данных, например, радиоканал Bluetooth , WiFi или подключение по кабелю, например, USB .

Предполагается обмен информацией между системой управления и ОБЗ для формирования БЗ (рис. 4).

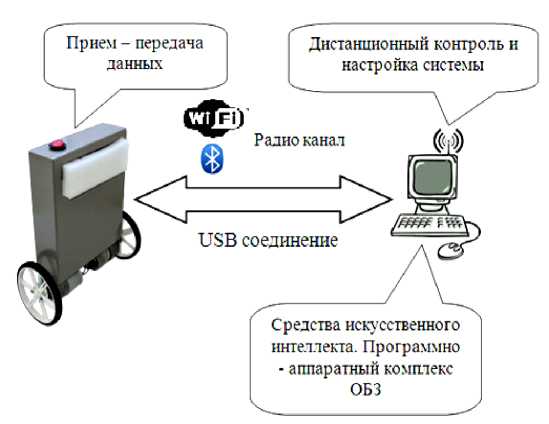
Рис. 4. Схема соединения настраиваемого устройства и ОБЗ

Подробно процесс настройки функционирования подобной системы представлен на (рис. 5).

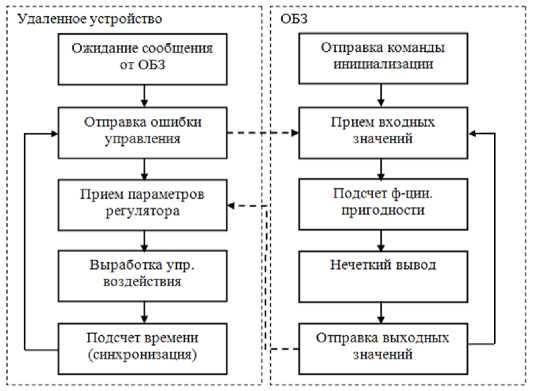
Рис. 5. Алгоритм работы удаленной настройки

Система управления считывает показания датчиков и отправляет их на компьютер для последующей обработки. Приняв входные значения, ОБЗ оценивает предыдущее решение (БЗ НР) и осуществляет нечеткий вывод для проверки следующего решения (БЗ НР). Результат нечеткого вывода

Электронный журнал «Системный анализ в науке и образовании» Выпуск №1, 2015 год отправляется на удаленное устройство. После этого, система управления, обработав входные значения, вырабатывает управляющее воздействие.

Прежде чем приступить к установке соединения между оптимизатором и системой управления необходимо установить физические ограничения взаимодействующих устройств, т.е. определить максимальные и минимальные временные границы одного такта системы управления с учетом приема, передачи и обработки сообщений.

Синхронизация ОБЗ и системы управления осуществляется на основе удаленного устройства (робота). С этой целью разработана специальная программа (прошивка), реализующая алгоритм, представленный на рис. 5.Профиль соединения использует последовательный порт. Скорость передачи в нашем случае составляет 115200 бит/с. В процессе функционирования, по COM-порту передаются числа с плавающей точкой в символьном виде. Подключение к ОБЗ осуществляется через разработанный плагин. Перед установкой соединения в окне ОБЗ следует выбрать номер СОМ-порта, скорости соединения и время проверки одного решения (количество тактов системы для проверки решения) (рис. 6).

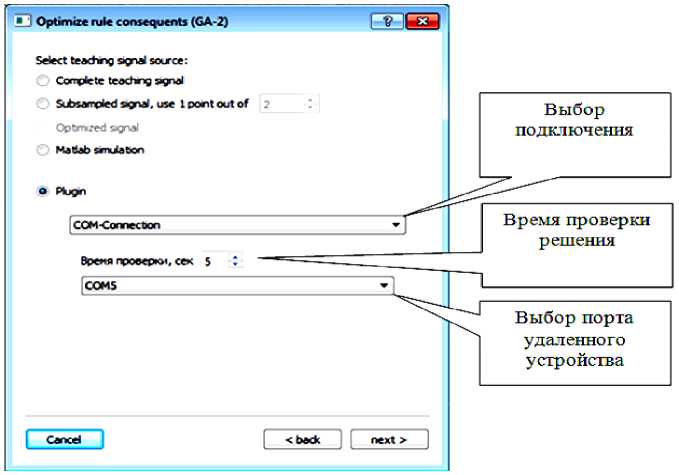
Время проверки решения

Выбор порта удаленного устройства

Optrnred signal

О Matlab emulation

Вреия проверки, сек 5

COMS

Выбор подключения

Рис. 6. Модуль удаленной настройки для ОБЗ

В качестве среды передачи данных рассмотрим возможность использовать модуль радиосвязи представлены на рис. 7для беспроводной настройки БЗ динамически неустойчивого объекта.

Рис. 7. Модуль радиосвязи Bluetooth

Установим физические ограничение временной задержки при приеме-передачи данных в коммуникационной среде. Временная задержка составляет 40 мс, что для типовых систем управления, рассмотренных ранее, является критичным. Исходя их этого, ситуацию управления с такой величиной задержки можно считать экстремальной.

Для решения задачи управления изменим закон формирования управляющего воздействия (1). Задающий сигнал системы стабилизации будет зависеть от интегральной ошибки (2), это позволит системе функционировать при критической временной задержки:

ref = — a - J edt , (2)

где а – экспериментально подобранный параметр равный 0.25. В выражении (2) угол задающего сигнала зависит от накопленной интегральной ошибки. Важно отметить, что дополнительно на величину задающего сигнала было наложено ограничение, и ее значение не должно выходить за приделы диапазона [ — 16,16 ] .

Закон управления и новая ситуация управления, требуют создания новых БЗ с использованием технологий, рассмотренных ранее. Представленные технологии проектирования ИСУ реализованы и поддерживаются в программном продукте [14, 15].

Объект управления

Управление объектом типа «Каретка – перевернутый маятник» является одной из типовых задач в теории управления, т.к. решение этой задачи наглядно демонстрирует качество САУ. Рассмотрим динамику модели в виде одноосевой каретки (рис. 8) с перевёрнутым маятником, закреплённым на оси.

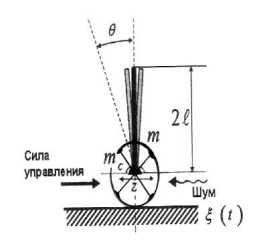
Рис. 8. Модель системы «Каретка – перевернутый маятник»

Динамика этого ОУ описывается системой дифференциальных уравнений второго порядка (3), выводимых, с учетом сил трения и упругости каретки, из баланса моментов и проекций сил на горизонтальную ось Z:

u + ^(t) - a,z — a^z + ml(0 sin 0cos0)

mc + m

g sin 0 + cos0

u + ^(t) + a,z + a2z — ml0 sin 0

— k0

0 =

к

mc + m

.

z .             ?

4 m cos 0

37-- к 3  mc + m J

Уравнения для скорости производства энтропии следующие:

S 0 =

k02 +1/2m0 sin20

l(mc + m) --

;

m cos 0

a 122

^S _z            * z ; ^S _u    kde .

mc + m

mc + m

Динамическая система обладает глобальной динамической неустойчивостью, при отсутствии управляющей силы происходит неограниченный рост угла отклонения, т.е. маятник падает. Задача управления системой состоит в том, чтобы, воздействуя с помощью силы управления на тележку, удерживать (стабилизировать) маятник в вертикальном положении (угол отклонения оси маятника от вертикали к 0) в условиях изменения среды функционирования.

Структура компьютерной модели «каретка - перевернутый маятник», выполненная в среде моделирования MatLab / Simulink , представлена на рис. 9.

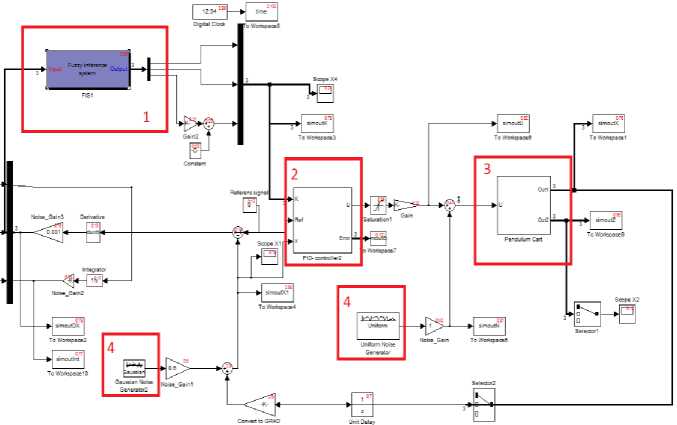
Рис. 9. Структура системы моделирования: 1 - блок нечеткого вывода; 2 - ПИД – регулятор;

3 - объект управления; 4 - генераторы шумов

Модель включает в себя ПИД-регулятор, шумы в системе управления и измерения, а также блок, формирующий сигнал для регулятора.

Данная компьютерная модели используется для получения обучающего сигнала и настройки БЗ с использованием ОБЗ. Основные этапы построения БЗ с использованием ОБЗ рассмотрены в [16]

В качестве модели управления данной системой, будем использовать выражение (1) для подсчета управляющего воздействия. В соответствии с этой схемой управления будем использовать ПИД-регулятор в контуре глобальной отрицательной обратной связи.

Данный тип ОУ является типовым ( benchmark ) для тестирования программного инструментария робастного интеллектуального управления. Примеры подобных систем рассмотрены в работах [2-8] и представлены на рис. 10.

Рис. 10. Аналоги рассматриваемого ОУ

Проектирование регулятора: моделирование и эксперимент

На втором этапе, ОС, подается на вход ОБЗ, который аппроксимирует его с помощью заданной пользователем модели нечеткого вывода. Выбирается оптимальное представление функций принадлежности лингвистической переменной.

Результат этапа построения входных лингвистических переменных представлен на рис. 11.

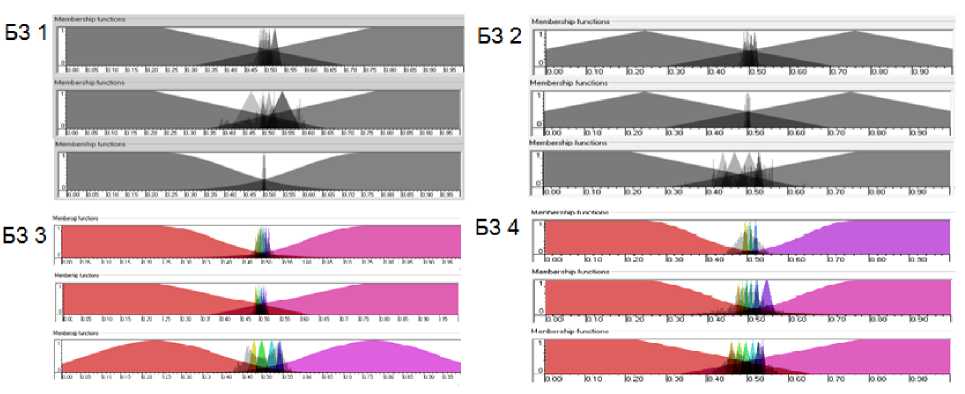
Рис. 11. Функции принадлежности для входных значений лингвистических переменных БЗ 1, БЗ 2, БЗ 3, БЗ 4

На этом этапе оптимизируются правые части правил. Для этого используется ГА2 (для ОС с макета) и Матлаб моделирование для ОС, полученных с использованием модели.

Результаты построения БЗ иллюстрируются ниже (рис. 12).

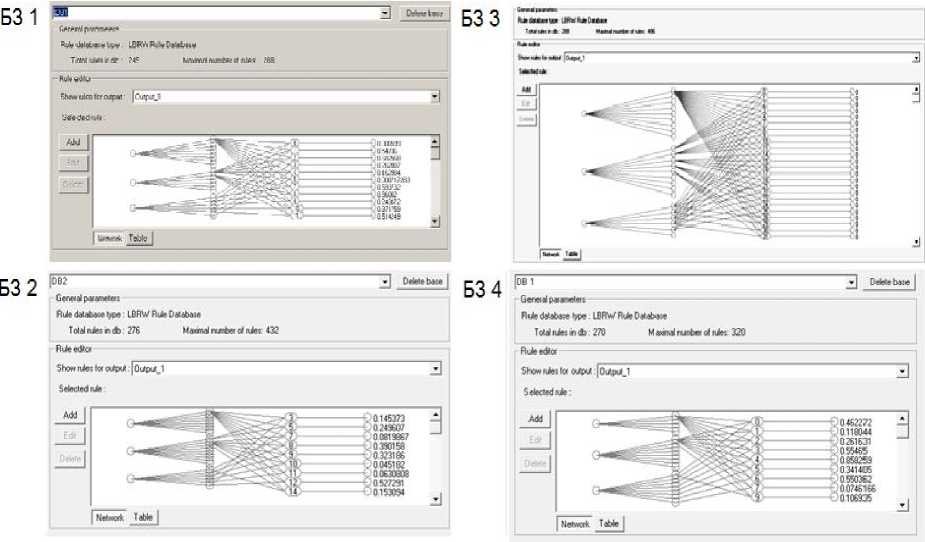
Рис. 12. Базы знаний в виде нейронных сетей (ОС с модели и макета)

Для формирования правых частей правил для БЗ, ОС которых получен с макета, использовался ГА2.Функция пригодности на данном этапе – минимум ошибки аппроксимации ОС. Результат создания и оптимизации правил БЗ представлен в виде нейронной сети на рис. 12. Первый слой демонстрирует количество входных переменных, второй – количество функций принадлежности для каждой переменной, третий – продукционные правила БЗ, четвертый – значения коэффициентов усиления.

На рис. 13 демонстрируется связь между обучающим сигналом полученного с использованием математической модели и коэффициентами усиления нечеткого регулятора.

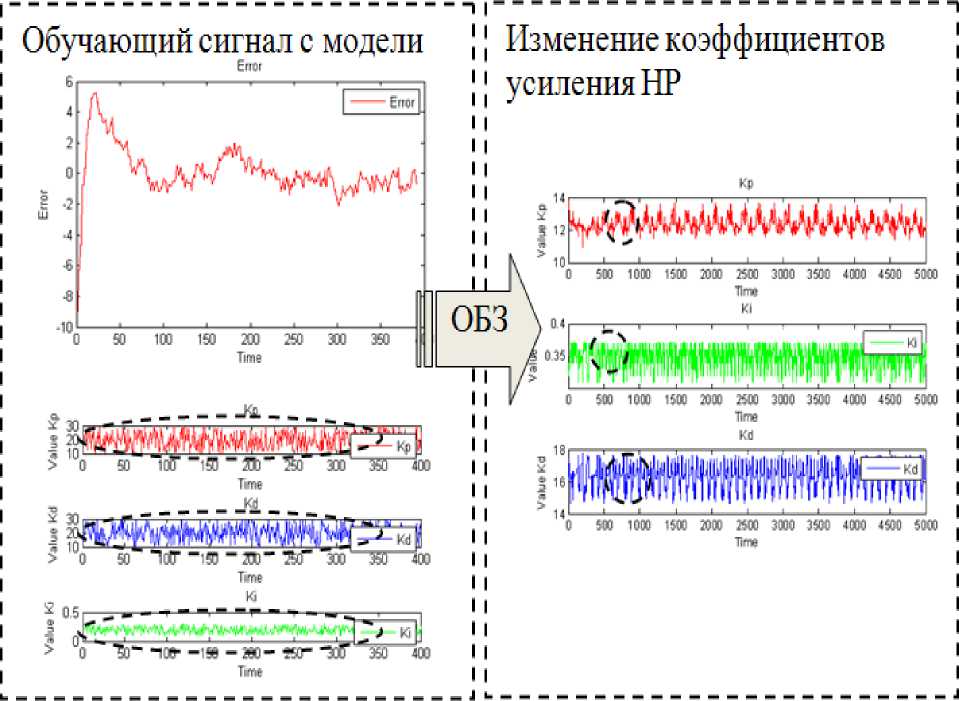
Рис. 13. ОС с модели и коэффициенты усиления НР

В таблице 1 приведено сравнение БЗ по количеству правил, количеству функций принадлежности лингвистической переменной и способу оптимизации в программном инструментарии ОБЗ.

Таблица 1. Сравнение БЗ

База №	Количество правил	Кол-во ф-ций принадлежности	Способ оптимизации
База 1 Модель	245	8х6х6	Моделирование
База 2 Модель	276	8х9х6	Моделирование
База 3 Макет	288	9х9х6	Аппроксимация ОС (ГА2)
База 4 Макет	270	5х8х8	Аппроксимация ОС (ГА2)

Исследование качества управления ПИД-регулятора и нечетких регуляторов на основе программного инструментария ОБЗ проводилось с использованием математической модели и реального ОУ. Регуляторы разрабатывались для функционирования в типовой ситуации управления. Параметры математической модели используемой для моделирования представлены в таблице 2.

Таблица 2. Ситуации управления, параметры математических моделей

	Типовая ситуация (С1)	Непредвиденная (С2)
Начальный угол	0гр	0гр
Начальная скорость	1гр/с	1гр/с

Масса тележки	0.56 кг	0.56 кг
Масса маятника	0.63 кг	0.63кг
Длина маятника	0.07 м	0.07 м
Трение в креплении	3.55 + нормированный шум с интенсивностью 0.01 и амплитудой 0.35	2.75 + нормированный шум с интенсивностью 0.01 и амплитудой 0.35
Трение колес	3.63 + Гауссовский шум 15%	2.53 + Гауссовский шум 15%
Сила упругости	5.54Н/м	7.54Н/м
Шум в системе управления	Равномерный [-2.15 2.15], интенсивность 0.48	Равномерный [-2.55 2.55], интенсивность 0.48
Шум в системе измерения	Амплитуда 0.22, Гауссовский шум, интенсивность 0.01	Амплитуда 0.42, Гауссовский шум, интенсивность 0.01
Задержка управляющего воздействия	0.01 с	0.01 с

Для сравнения робастности разработанных систем управления используем непредвиденную ситуацию управления. Ситуация моделируется наличием шума в коэффициенте трения колеса о поверхность и в управляющем воздействии. В качестве такого шума в эксперименте используется специальное покрытие, а для моделей были установлены соответствующие значения параметров.

На рис. 9 представлена структура системы моделирования. Рассмотрим поведение ПИД- и нечетких регуляторов в типичной и непредвиденной ситуации управления. На рис. 14-17 представлены результаты моделирования и экспериментов в типовой ситуации управления:

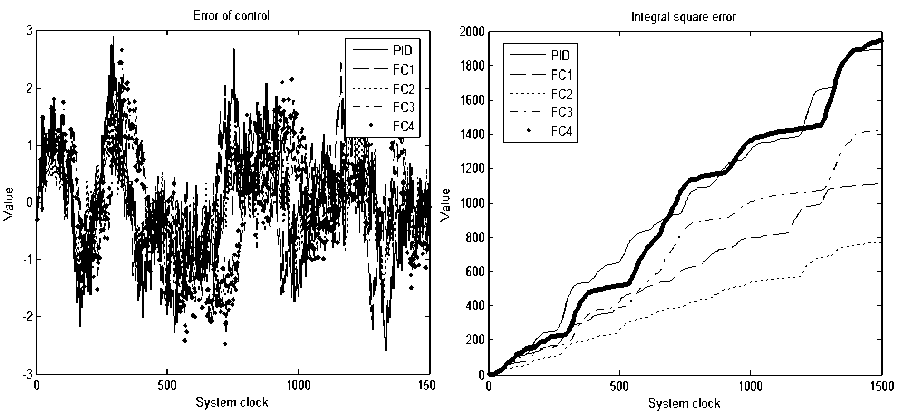
Рис. 14. Слева ошибка управления, справа интеграл квадратичной ошибки. Типовая ситуация управления. Моделирование

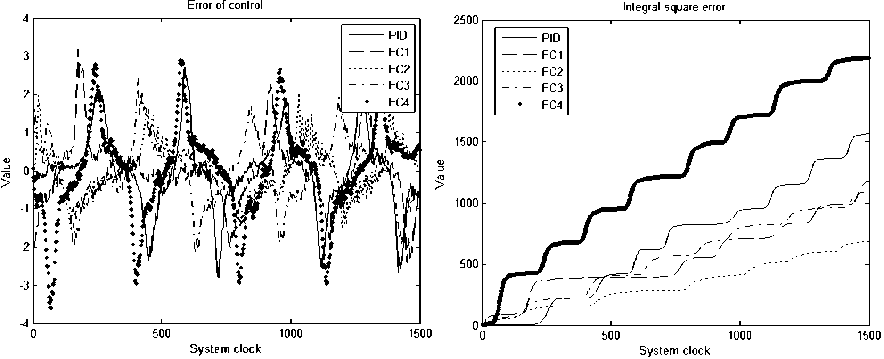
Рис. 15. Слева ошибка управления, справа интеграл квадратичной ошибки. Типовая ситуация управления. Эксперимент

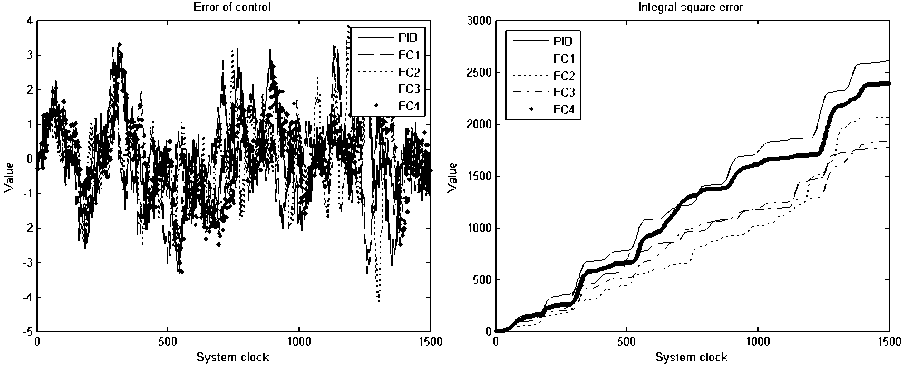
Рис. 16. Слева ошибка управления, справа интеграл квадратичной ошибки. Непредвиденная ситуация управления. Моделирование

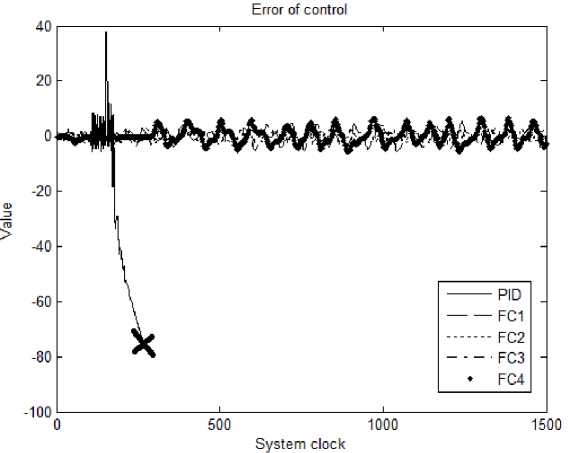
Рис. 17. Ошибка управления. Непредвиденная ситуация. Эксперимент

Проведем анализ качества управления НР и ПИД регуляторов. Для этого используем следующие показатели переходного процесса (рис. 18):

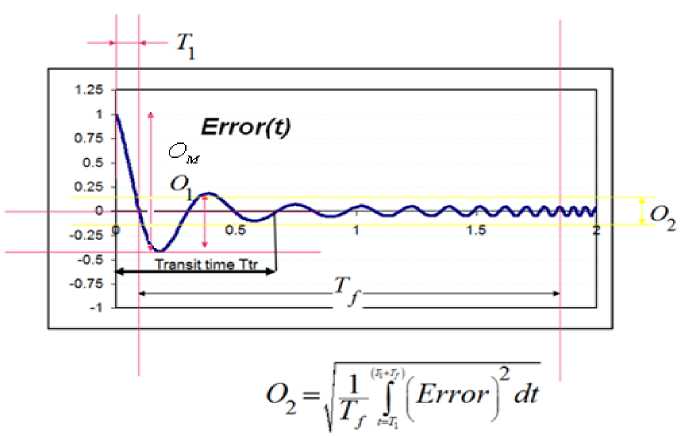
Рис. 18. Показатели качества управления

Перерегулирование характеризует колебательное свойство переходного процесса и рассчитывается согласно следующему выражению:

Ц = 1 - —; O_m ( const .) >  O [.

^Om   ^m

На рис. 19 представлена диаграмма уровня перерегулирования систем управления. Нечеткий регулятор, разработанный на основе верифицированной математической модели, имеет более низкий показатель перерегулирования, что характеризует работу такого регулятора как более эффективную.

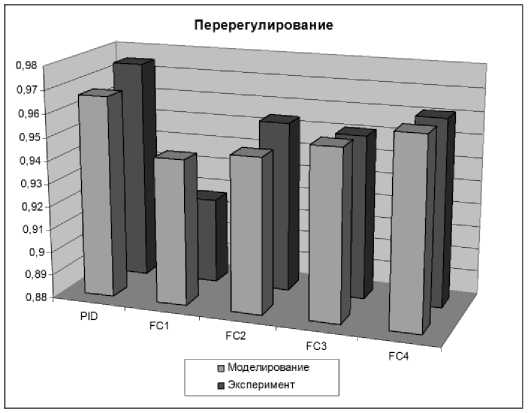
Рис. 19. Перерегулирование систем управления в типовой ситуации. Моделирование и эксперимент

Устойчивость переходного процесса регуляторов (рис. 20) рассчитывается как:

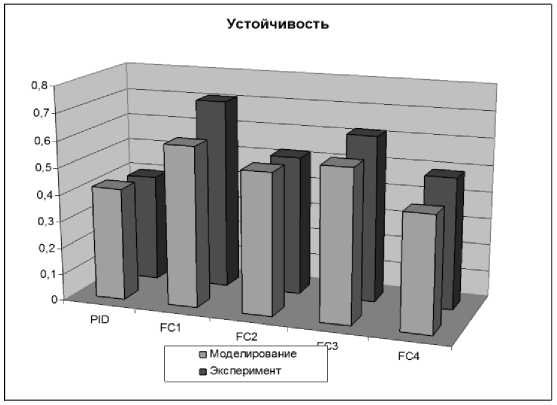
Рис. 20. Устойчивость систем управления в типовой ситуации. Моделирование и эксперимент

Качество управления характеризует способность системы управления эффективно расходовать энергетический и технический ресурс системы. В случаи реализации сложного управления, износ оборудования и затраты энергии будут велики.

Сложность управления САУ (рис. 21) рассчитывается в виде:

P = 1 -

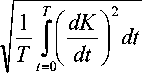
A

; A = ( const ).

V                7

Оценка сложности управления показала, что нечеткие регуляторы, разработанные с использованием ОБЗ, обеспечивают систему более простым управлением, что в конечном итоге положительно сказывается на сроке использования оборудования, снижая износ и повышая надежность.

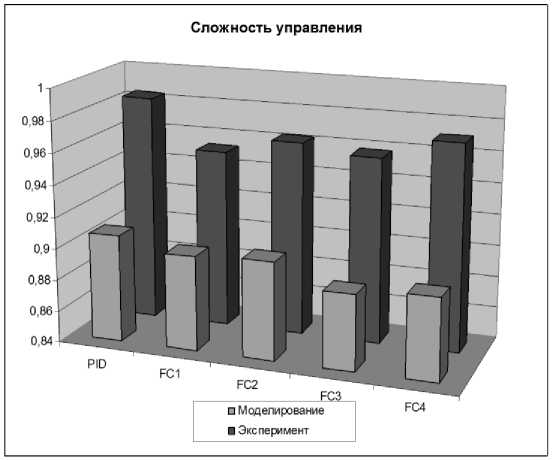
Рис. 21. Сложность управления в типовой ситуации. Моделирование и эксперимент

Результаты моделирования и эксперимента в непредвиденной ситуации представлены в графическом виде на рис. 14-17. Из графиков (рис. 19-21) видно, что ПИД-регулятор не обладает необходимой робастностью, что в непредвиденной ситуации управления приводит к потере устойчивости системы.

Заключение

Классические системы управления не всегда успешно справляются с задачей управления в случае, если ОУ является глобально неустойчивым илисущественно нелинейным, при наличии шумов или времени задержки в каналах измерения; а также при наличии стохастических шумов, особенно типа Рэлеевских (с несимметричной функцией плотности распределения).

Нечеткие контроллеры, основанные на традиционных инструментариях мягких вычислений, в которых структура нечеткой нейронной сети строится вручную экспертом, уступают в качестве управления и робастности нечетким контроллерам, построенным на основе Оптимизатора Баз Знаний.

Результаты моделирования и эксперимента показывают, что FC 4, разработанный без использования математической модели, не обладает достаточной робастностью.

FC 1, разработанный только на основе математической модели ОУ, обладает лучшей робастностью. Следует отметить, что и FC5 , разработанный на основе совместного использования математической модели и дистанционной настройки, обладает достаточно хорошим качеством управления. Этот регулятор FC 5 в типовой и непредвиденной ситуации справляется с задачей управления на достаточно высоком уровне.

Оптимизация БЗ с использование дистанционного соединения с ОУ непосредственно напрямую с ОБЗ даёт ряд преимуществ:

• -    позволяет не строить математическую модель и при этом получать знания об ОУ для построения БЗ;

• -    для проектирования ИСУ в ОБЗ достаточно снять информативные показатели и параметры поведения ОУ;

• -    дистанционное соединение позволяет оптимизировать БЗ в определенных (типовых) условиях функционирования, тем самым создавать множество БЗ с высоким качеством управления для различных ситуаций управления.

Результаты моделирования широкого класса объектов управления показали, что разработанная технология ИТП ИСУ и разработанный инструментарий ОБЗ демонстрирует хорошие качества управления и робастность, несмотря на изменения (непредсказуемые) широкого класса факторов, таких как изменение внешних шумов, изменения параметров модели ОУ, изменение времени задержки в каналах измерения, изменение цели управления.