Применение теории эволюционной оптимальности для определения преждевременной и избыточной смертности в модели Лотки

«Московский физико-технический институт (национальный исследовательский университет)», 2024

обусловлено индивидуальное бессмертие и почему в природе оно практически ненаблюдаемо? Все эти вопросы разбираются в рамках теории эволюционной оптимальности применительно к модели Лотки, описывающей динамику популяции с непрерывной возрастной структурой.

Напомним, что в основе принципа эволюционной оптимальности лежат ключевые постулаты дарвиновской теории эволюции: наследственность, изменчивость и отбор [1]. В используемых для обоснования этого принципа простейших математических моделях [2] второй из постулатов явным образом не учитывается. Его неявный учет сводится к предположению о том, что изменчивость уже сыграла свою роль в формировании возможных условий для развития видов, обладающих преимуществами по отношению к потенциальным конкурентам. Считается, что для таких видов характерна строгая наследственность, а отбор уже произошел, так что сформировалось устойчивое равновесное состояние, в котором остались только выжившие в процессе конкуренции виды. Устойчивость при этом формулируется уже в терминах подходящих математических моделей, как правило, автономных, т.е. не зависящих явным образом от времени, и понимается в смысле устойчивости положений равновесия, соответствующих сформировавшимся устойчивым равновесным состояниям моделируемой системы. Такая устойчивость эквивалентна одновременному выполнению двух ее частных случаев: внутренней устойчивости, т.е. по отношению к малым возмущениям численностей присутствующих в указанном состоянии видов, и внешней устойчивости, т.е. по отношению к внедрению малых количеств особей видов, отсутствующих в этом равновесном состоянии. Именно последний из случаев устойчивости является основой математической формулировки принципа эволюционной оптимальности в качестве необходимого условия присутствия выживших видов.

Принцип эволюционной оптимальности базируется на построении функционалов отбора, являющихся математическим отражением дарвиновской «силы вида» в классической формулировке о выживании сильнейших. В своей простейшей, т.е. точечной, форме в качестве таких функционалов выступают [2] мальтузианские функции, стоящие в виде сомножителей при фазовых переменных в правых частях уравнений, в совокупности описывающих динамику моделируемого биологического сообщества. При этом параметры отбора могут быть самыми разнообразными - от простейших физиологических характеристик до функций, определяющих системные взаимосвязи у целого организма. На этом пути было получено много интересных результатов, позволяющих «на кончике пера» находить ответы на вопросы как философского (точнее, телеологического), так и практического характера. Многочисленные примеры последних можно найти, например, в [4].

Для случая распределенных систем потребовался более изощренный подход к конструированию функционалов отбора. Это, в частности, относится и к моделям биологических систем, наделенных возрастной структурой. Здесь, правда, еще со времен работ Лотки [3] известен так называемый биологический потенциал, характеризующий среднее число потомков в расчете на одну особь на протяжении всей ее жизни. Как оказалось, этот потенциал может успешно исполнять роль искомого функционала. Однако такие, на первый взгляд, простые характеристики, как максимальная продолжительность жизни, не поддавались моделированию в рамках принципа эволюционной оптимальности. Это было связано, главным образом, с тем, что в рамках свойств стационарных решений такая оптимальная продолжительность оказывалась бесконечной: у единственной выжившей в процессе конкурентного отбора популяции с установившейся численностью не было никаких оснований жертвовать какой-либо своей частью. В рамках модели Лотки этот факт подробно обсуждается во третьем разделе настоящей статьи.

Наиболее общая математическая модель, описывающая принцип эволюционной оптимальности для структурированных систем, изложена в [5]. С базирующимися на ней результатами, относящимися к системам с пространственной и возрастной структурой, можно ознакомиться в [6]. В частности, в [7] (см. также [8]) представлены результаты, пригодные для их непосредственного применения к модели Лотки. По техническим причинам в рам- ках общей теории эволюционной оптимальности для модели Лотки предполагалось, что функция рождаемости не входит в число факторов эволюционного отбора, т.е. остается заданной извне. Из-за этого приходится ограничиваться только факторами, привязанными к смертности. Здесь уже окно возможностей оказывается практически беспредельным. Смертность можно считать не только нелинейной функцией фазовых переменных, но и функцией произвольных распределений последних, включая как суммарные, так и относительные численности, интегральные характеристики с произвольными весами и т.п. В настоящей работе использованы два варианта таких характеристик: суммарная численность популяции и ее относительная численность по отношению к числу новорожденных.

Работа состоит из шести содержательных разделов. Во втором разделе приводится классическая модель Лотки [3] в форме уравнений Мак Кендрика - фон Ферстера (см., например, [9] или [10, 1.2]) с поправкой на функцию смертности, имеющую обозначенный выше вид и на включение ее в систему уравнений, описывающую сообщество популяций с возрастной структурой. В целях применения к такой модели принципа эволюционной оптимальности мы ограничиваемся автономным случаем, т.е. случаем, при котором входные функции не зависят явным образом от времени. Представленная в этом же разделе формулировка принципа эволюционной оптимальности для модели Лотки имеет здесь по-прежнему наиболее общий характер.

Начиная с третьего раздела предполагается, что выжившим оказывается только один из числа конкурировавших видов. Отбор при этом осуществлялся по таким факторам, как избыточная смертность и сокращение продолжительности жизни сверх пределов, обусловленных естественными причинами. Конкретно к этому разделу относится случай, когда популяционное влияние на смертность оказывается опосредованно только через суммарную численность популяции. Оказалось, и это основной результат этого раздела, что при задаваемых таким образом условиях взаимодействия особей в популяции избыточная смертность, равно как и преждевременный уход из жизни, могут проявляться только после окончания фертильного периода особей и то лишь в факультативной форме. Бесконечная же продолжительность такого периода обеспечивает особям индивидуальное бессмертие, насколько это возможно при наличии внешних воздействий. Здесь же обсуждается так называемый парадокс бессмертия: почему «бессмертные» популяции почти не наблюдаемы в природе.

Начиная с четвертого раздела предполагается, что смертность зависит от популяционных влияний опосредованно только через отношение суммарной численности популяции к числу новорожденных. Приводится обоснование допустимости такой зависимости и строятся основные модельные характеристики, включая функционалы отбора, используемые в последующих разделах.

В пятом разделе строятся вариации представленных ранее основных модельных характеристик при малых вариациях оптимизируемых параметров избыточной смертности и максимальной продолжительности жизни.

В шестом разделе в предположении оптимальности параметра избыточной смертности указываются необходимые условия, существенным образом сужающие спектр допустимых значений этого параметра. Вводятся такие понятия, как стандартная функция рождаемости, допустимая избыточная смертность и плотностный профиль биологического потенциала. Доказывается, в частности, что для такой функции рождаемости допустимая избыточная смертность не меняет плотностного профиля.

В седьмом разделе в предположении оптимальности параметров избыточной смертности, времени жизни и относительной суммарной численности популяции строится соотношение, позволяющее вычислить недостающие оптимизируемые характеристики. В случае вполне естественного модельного предположения о мультипликативном по возрасту и относительной численности виде функции смертности на основе этого соотношения доказывается, что относительная численность должна доставлять минимальное значение популяционной составляющей смертности. Результат проиллюстрирован численным примером, демонстрирующим возможность обрезания продолжительности жизни «по-живому», т.е.

еще до окончания фертильного периода.

• 2.    Модель Лотки и принцип эволюционной оптимальности для нее

В рамках моделей сообществ популяций с непрерывной возрастной структурой, представляющих собой в неавтономном случае обобщение модели Лотки в форме Мак Кендрика - фон Ферстера, исходная автономная модельная система уравнений имеет вид dxx + dxx dt да

= -т_хх х ,

A € Л

с краевыми условиями

Ту xx(0,t) = bx(a)xx(a,t) da, A € Л и подходящими начальными условиями

xx(0, а) = x X (a).

Здесь t ^ 0 - время, а ^ 0 - возраст, x x = x x (t,a) ^ 0 - возрастная плотность популяции в момент времени t, имеющей номер A € Л из возможно произвольного множества Л, T x С го - максимально допустимая продолжительность жизни особей популяции с номером A. Предполагаемая автономность означает, что каждый из коэффициентов смертности m x = m x (x,a) особей вида с номером A зависит лишь от возраста a самих этих особей и значений вектора состояния x = x(t) = {x x (t, ДА € Л} структуры сообщества. Отметим, что точка на месте аргумента означает, что данный аргумент пропущен, т.е. зависящее от него выражение не вычисляется для какого-то конкретного значения аргумента, а учитывается во включающем его соотношении (в целях сокращения многозначности этот термин употребляется здесь как синоним математического понятия отношения, которым может быть равенство, неравенство и т.п.) целиком, т.е. как функция. В частности, предполагается функциональная зависимость коэффициентов смертности от состояния сообщества в целом (например, от таких его интегральных характеристик, как общая или относительная численность, взвешенная возрастная структура и т.п.).

Заметим, что использование конечных значений для T x позволяет избежать необходимости учета возможных бесконечных значений для m x (x,a) = о© при a ^ T x (такая альтернативная постановка задачи с T x = го для всех А € Л, будучи эквивалентной исходной, не представляется удобной с технической точки зрения).

Постоянные по времени коэффициенты рождаемости b x (a) ^ 0 считаются не зависящими от текущих распределений x. Все исходные функции (т.е. m x и b x) при каждом значении А считаются непрерывными кусочно-гладкими по всем своим аргументам.

Заметим, что в случае двуполых популяций в модели (1) - (3) можно принимать в расчет одних только самок, учитывая самцов лишь в рамках их влияния на коэффициенты смертности m x опосредованно через самок из соображений пропорциональности. Это означает, в частности, что в (2) коэффициент b x (a) будет представлять собой число новорожденных самок популяции с номером А за единицу времени, приходящихся на одну мать возраста a в момент времени t.

Корректная разрешимость задачи (1) - (3) для различных вариантов ограничений на исходные данные доказывалась в работах [10], [11]. Не углубляясь в детали, отметим здесь, что в рассматриваемом в настоящей работе варианте (см. условия ниже) такая задача корректно разрешима, т.е. имеет единственное решение в области R+ = {(t, a) : t ^ 0,a ^ 0}, непрерывным образом зависящее от исходных данных. Это решение монотонно по x^a), и, стало быть, неотрицательно при x x (a) ^ 0.

В рамках моделей указанного типа принцип эволюционной оптимальности может быть сформулирован следующим образом.

Если система (1), (2) имеет устойчивое положение равновесия ж = {жд(а), А G Л}, то для А G вирр(ж) (подмножество тех значений параметра А G Л, для которых жд(а) не обращается тождественно в нуль) выполнено соотношение

1 = В (А) =max В (А) дел с функционалом отбора га /а \

В (А) = Ьд(а)ехр l-^ mд(ж,s) ds I da. (5) 00

Содержательный смысл функционала (5) - это биологический потенциал популяции с номером А, т.е. среднее число рожденных одной особью на протяжении всей ее жизни.

С практической точки зрения для нахождения тех значений параметра А, которые реализуются для априори известного установившегося стационарного распределения ж, следует решить задачу максимизации (4) по А для функционала (5). Заметим, что равенство единице теоретического максимального значения этого функционала означает не что иное, как стационарность распределения ж.

В качестве параметра отбора А могут фигурировать любые выражения, характеризующие свойства видов. В моделях предполагается их неизменность, так что единственным механизмом формирования свойств, присущих выжившим видам, является конкурентный отбор. Это означает, что принцип эволюционной оптимальности устанавливает запреты на использование в моделях выражений, соответствующих нежизнеспособным видам. Другими словами, если для некоторого стационарного распределения ж и А G вирр(ж) найдется А / вирр(ж) такое, что В (А) >  В (А), то на А накладывается запрет, поскольку распределение ж не является устойчивым с точки зрения возможности внедрения видов, входящих в конкурирующий набор, задаваемый параметром А. При этом для того, чтобы воспользоваться формулой (5), вовсе не обязательно знать само распределение ж, если в указанной формуле фигурируют лишь некоторые общие характеристики этого распределения, - достаточно знать только сами эти характеристики.

Характерное время существования равновесного состояния существенно превосходит характерное время, необходимое для установления такого состояния. Однако в условиях постоянно изменяющихся внешних воздействий, зачастую приводящих к разрушению установившихся стационарных режимов, не исключаются ситуации, когда эволюционный отбор происходит не по признакам доминирования в установившихся равновесных распределениях, а уже в процессе изменений, обусловленных этими внешними воздействиями. Наиболее простым вариантом неравновесных моделей являются модели магистрального типа. В таких моделях вместо устойчивого равновесного состояния ж рассматривается устойчивый рост с некоторым показателем у G R. Имеется в виду устойчивое равновесное состояние системы (1) - (2) относительно переменных возрастного профиля ж⁷ = {жд(t, а), А G Л} с жДД, а) = е^{-7^}жд(t,a). С математической точки зрения магистральные модели отличаются от стационарных лишь показателем у, добавляемым к смертности, при рассмотрении возрастного профиля в качестве стационарного решения. Действительно, подстановка жд(t,a) = е^{7^}ж7(t, а) в (1) дает относительно жД(£, а) уравнение (1) с тд(ж,а) +у вместо тд(ж, а). С биологической точки зрения показатель у можно рассматривать как гандикап роста - своеобразную плату за возможность развития вместо неизменности. Заметим, что случаю у < 0 соответствует экспоненциальное убывание численности, т.е. исчезновение вида, так что этот вариант с прикладной точки зрения особого интереса не представляет.

В случае жесткого конкурентного отбора, т.е. когда в устойчивом равновесном состоянии на одну экологическую нишу согласно принципу конкурентного исключения Гаузе [12] приходится не более одного вида, принцип эволюционной оптимальности может быть описан в терминах одной стационарной (по отношению к времени t) фазовой переменной

х(а) = хд(а), характеризующей возрастную плотность популяции такого выжившего вида. С учетом стационарности получаем вместо (1) и (2) соответственно dx da

—m(x(•'), а)х,

И

x(0) = I b(a)x(a)da                                     (7)

'0

c m(x(•),a) = m д (x(^),a) . b(a) = Ь д (а) ii Т = Т д С от. Параметр отбора А при атом состоит из входных параметров задачи (6) - (7), т.е. из максимальной продолжительности жизни Т и смертности m. Далее мы исключаем функцию b(a) из числа параметров отбора, т.е. считаем ее фиксированной. Содержательно такая гипотеза означает, что отбор производится среди конкурирующих (под-)популяций, имеющих одинаковые функции рождаемости. Смысл и вид учитываемых параметров отбора требуют уточнения. Так, параметр Т обрезает, т.е. обнуляет популяцию при а > Т, так что независимо от всех прочих обстоятельств особи старше Т считаются мертвыми. В качестве одного из параметров отбора А G Л памп будет рассматриваться избыточная смертность v(а) ^ 0. Зависимость от нее мы будем помечать нижним индексом, так что то(х(ф а) = m(x(•), а) и m ^ (x(-), а) = m o (x() а) + v (a). Функция v (а) считается кусочно-непрерывной (т.е. непрерывной по крайней мере слева или справа для каждого значения аргумента) функцией возраста. Популяционные факторы отбора рассматриваются в двух вариантах. Об это идет речь в следующих ниже двух разделах.

• 3.    Случай зависимости функционала отбора от общей численности

Пусть

W(Т,х⁰) = ^ x(a)da                                 (8)

• - интегральная (т.е. общая) численность популяции до возраста Т С от, динамика которой описывается моделью (6) - (7) с m(x(•),a) = m(W(Т,х°),а) >  0 и x(0) = x⁰ >  0. При наличии избыточной смертности v(а) ^ 0 вместо W(Т,х° пишем W_u(Т,х°).

Положим ТЬ = зир{а : Ь(а) >  0} С от.

Теорема 1. Пусть m(x(•),a) = m(W_u(Т,х⁰),а) > 0, Ть С от и х(а) = Хд(а) - решение задачи (4) - (7). Тогда рассматриваемая в качестве одного из параметров отбора избыточная смертность отсутствует, т.е. v(а) = 0 для а G [0,ТД причем Т ^ ТЬ может быть любым.

Доказательство. В рассматриваемом случае А = (Т, v, х⁰), так что функционал (5), имеет вид

В (Т,ы,х⁰^ = I Ь(а)ехр I —/ (m(W^(Т, х⁰), s) + v(s))ds ] da.             (9)

Зафиксируем некоторые Т С от, х⁰ и W = W_y(Т,х°). Положим Т™ = ш!п{Т,Т_ь}. В предположении v(a) >  0 на некотором интервале а € (а, а + е ) С [0, Т™] можно, заменив v(а) >  0 на 0 и уменьшив тем самым смертность m^(W,a), добиться увеличения решения задачи Коши х(а) для (6) при а > а, включая и те значения а € (а,Т™~), для которых Ь(а) > 0. За счет этих значений произойдет увеличение функционала (9), в котором на месте W_y(Т,х° стоит W, так что будет выполнено неравенство В Т^, 0, Х⁰) > В (Т,и,х⁰'). Возникающий при этом рост W0 (Т, Х⁰) > W_u (Т, Х⁰) может быть скомпенсирован за счет подходящего уменьшения х⁰< Х⁰ в силу линейности (6) таким образом, чтобы в выражении (8) величины Т и W(Т,х°) = W остались прежними. Функционал (9), зависящий от х⁰ только опосредованно через W^(Т,х°) при этом возрастет, ибо в случае

W(Т,х°) = W = W , (Т,х°') будет В (Т, 0,х°) >  В ( Т, 0,х°), что означает отсутствие его

оптимальности в условиях сделанного предположения.

Те же соображения в случае v(a) = 0 и Т < Т позволяют увеличить функционал

(9). увеличив Т. Этого можно добиться, сделав замену Т м Т ‘ = Т + т > Т. выбрав

некоторое т таким образом, чтобы нашлось a G (Т,Т + т ), для которого выполнялось неравенство b(a) >  0. При этом но вое значение х°* следует подбирать таким образом, чтобы выполнялось равенство W° (Т ' ,х ° *^ = W ° (Т,х⁰)- В этом случае для a G (Т,Т + т )

будет выполнено неравенство

^т + ^т

( b(a) exp т

— — ( m(W_t(Т,х°), s)ds^

da >  0. При этом выбор

любого Т ^ Т^ на значение функционала (9) не влияет.

С учетом теоремы 1 отыскание оптимального решения задачи (4) - (7) с m(х(•),a) = m(W_t(Т,х°У) для Т ^ Т ^ может быть проделано следующим образом. Построим функцию Ф(Х) = В (Т ^ ,^ ° (Т ^ ,Х )). г,тс £, (Т,Х ) - начально е 'значение х°. обес

печивающее для интегральной численности (8) к моменту времени Т при заданной функции избыточной смертности v = v(а) некоторое наперед заданное значение Х, так что W , (Т,^ „ (Т,Х )) = Х. В случае монотонного возрастания т(Х, •) (возрастание смертности с увеличением численности - это случай внутривидовой конкуренции) функция Ф(Х) будет монотонно убывать, так что решение Х уравнения (см. первое равенство в (4))

Ф(Х) = 1,

если таковое существует и единственно, даст оптимальное распределение

х(a) = х ° exp

— — ( т(Х, s)ds^ ,

(И)

с

т

а

х °

exp

-

I т(Х, s)ds I da.

В (12) максимальная продолжительность жизни Т ^ Т ^ является свободным управляющим параметром. Монотонное убывание х ° с ростом Т имеет естественную биологическую интерпретацию, означающую сокращение рождаемости при увеличении продолжительности жизни. При нарушении равенства (10) в случае Ф(Х) < 1 (в случае монотонного возрастания т(Х, •) это будет иметь место при избыточной общей численности, т.е. при Х > Х вместо Х в (12)) наиболее эффективной биологической стратегией является стратегия, основанная на уменьшении Т, т.е. направленная на сокращение части популяции, вышедшей за пределы фертильного возраста. Механизмы такого сокращения могут обеспечивать различную скорость процесса, но так или иначе должны рассматриваться на популяционных характерных временах (т.е. порядка времени созревания до взрослого, т.е. фертильного, состояния, или, что то же самое, порядка среднего времени жизни отдельной особи) как моментальные. Такая картина наблюдается, например, у многих видов насекомых, рыб и т.п., когда особи после оплодотворения почти сразу же теряют жизнеспособность. Альтернативной стратегией в этом случае может служить сокращение рождаемости х°, приводящее к восстановлению равновесия в условиях указанного нарушения лишь через поколение, т.е. за время, характерное для продолжительности жизни особей рассматриваемой популяции. Такое же время понадобится для восстановления равновесия посредством увеличения х ° (если, конечно, таковое возможно) в случае противоположного нарушения, т.е. при Х < Х, при том, что для указанного восстановления достаточно предоставить старикам (т.е. особям, вышедшим за пределы фертильного возраста) достаточно комфортные условия для более длительного проживания, так что процесс восстановления произойдет за время, равное времени этого дополнительного проживания.

В случае, когда Ф(Х) < 1 для всех допустимых X, популяция будет иметь биологический потенциал, меньший единицы, т.е. будет вымирать. По этой причине указанный случай с точки зрения практических приложений интереса не представляет. В противоположном случае Ф(Х) > 1 численность должна неограниченно возрастать, так что она должна ограничиваться внешними факторами, не учитываемыми в модели. Их учет может быть осуществлен подменой задачи с растущей численностью на задачу с постоянной численностью (например, за счет задания подходящим образом убывающего начального ж⁰) с одновременным увеличением функции m(X, •), т.е. добавлением гандикапа роста у > 0, обеспечивающим уменьшение Ф(Х), что может позволить добиться выполнения равенства (10). Обратим внимание на то, что в случае отсутствия сдерживающих внешних факторов для поддержания выполнения равенства (10) потребуется исчезновение ж⁰ ^ +0, что свидетельствует о ненаблюдаемости (см. ниже про парадокс бессмертия) видов с такими свойствами.

Более интересная ситуация возникает, когда Т^ = той наружный интеграл в (9) расходится при Т ^ то. С биологической точки зрения приведенное равенство означает, что особи популяции могут оставаться фертильными сколь угодно долго, возможно не всечасно и возможно в очень незначительной степени. Расходимость интеграла означает при этом крайнюю слабость воздействия смертоносных факторов. В обозначенном случае в силу (12) будет выполнено равенство ж⁰ = 0, так что в силу (11) окажется выполненным равенство ж(а) = 0. Оно означает, что популяция с такими свойствами также не может претендовать на ее использование для описания реальных выживших популяций с возрастной структурой. Указанная расходимость может иметь место, например, в случае выполнения неравенства m(X, a) С Са^-1 при всех достаточно больших а и некотором С >  0. В более реальной ситуации, когда наружный интеграл в (9) сходится, но достаточно велик, получаемое из (12) значение для ж⁰ будет очень малым, что позволяет говорить о незначительности (в смысле ненаблюдаемости) популяций с малой естественной возрастной смертностью. Такой парадоксальный на первый взгляд результат, состоящий в том, что если при благоприятных условиях отдельные особи популяции могут размножаться бесконечно долго и воздействие смертоносных факторов крайне слабо, то такая популяция ненаблюдаема, мы называем парадоксом бессмертия.

Естественным методом преодоления парадокса бессмертия представляется включение в число популяционных механизмов как ограничения рождаемости для особей преклонного возраста, так и снижения сопротивляемости факторам естественной смертности. Включение же таких факторов, как избыточная по отношению к естественной смертность и сокращение максимального срока продолжительности жизни особей популяции, в рамках рассмотренной в настоящем разделе модели не предусматривается. Эти факторы можно наблюдать, если модель немного видоизменить, используя вместо абсолютной численности популяции (8), фигурирующей в популяционной составляющей смертности т(ж(^),а), подходящую относительную величину.

• 4.    Случай зависимости функционала отбора от относительной численности

Снова рассмотрим модель (4) - (7), в которой популяционная составляющая смертности предполагается зависящей уже от относительной численности, т.е. т(ж(фа) = m(U,a) с U = U_y(Т, ж⁰) = ^^^^) , где W_p(Т, ж⁰) - интегральная численность популяции до возраста Т С то (см. (8)), так что с учетом (6) а ( (m(U,s)+v(s))ds

U = J' exp (

) ^da .                        (13)

Величина U имеет содержательный смысл числа особей, доживших до возраста Т. в расчете на одного новорожденного. Заметим, что от параметра ж⁰ она как решение уравнения (13)

явным образом не зависит. Функционал отбора (5), также явно не зависящий от параметра ж⁰ , имеет в этом случае для А = (u, Т, U ) вид

т

B_v (Т, U) = f b(a) exp

—- f (m(U, s) + u(s))ds^

da

c U = U y (T, ж⁰) из (13). Замет им, что в (14) U фигурирует в качестве свободного параметра отбора. Отметим также, что такой вид функционала представляется вполне естественным в случае популяции, распределенной на достаточно большом ареале таким образом, чтобы внутривидовые взаимодействия, включая конкуренцию, затрагивали только особей, обитающих по соседству друг с другом. Распространение популяции по ареалу здесь в явном виде не рассматривается. Его можно подразумевать, полагая, что распространение вширь происходит по мере формирования устойчивого равновесного состояния популяции на уже заселенной территории.

В последующих разделах решается задача максимизации функционала (14) по набору неотрицательных параметров (u,T,U):

By (T,U) ^ max,(15)

связанных между собой соотношениями (13), при условии стационарности вида

By (T,U) = 1(16 )

для оптимальных значений (u,T,U). Введем дополнительные функции.

Накопленная к возрасту a смертность:

py (a,U) = f(m(U,s)+ u (s))ds.(17)

Вероятность дожития до возраста a:

Fy (a,U)=exp(-py (a,U)).(IS)

Число особей возраста s C a в расчете на одного новорожденного:

Gy(a,U) = I Fy(s,U)ds.(19)

Биологический потенциал части популяции возраста s C a:

B y (a, U ) = У b(s)F y (s, U)ds.                               ( 20 )

Заметим, что под знаком интеграла в (19) и (20) функция u входит целиком, т.е. как u = u (•). а нс как u (s). поскольку пр и вычислении p_y (a,U ) в (17). а. стало быть, ii F_y (a,U ) в (18), используются значения u(s), задаваемые на всем интервале s G (0,a).

Замечание. Положительная функция F_y(a, U ) в случае у ^ 0 является строго монотонно убывающей. Функции G_y(a,U ) и B_y(a,U ) являются соответственно строго монотонно возрастающей и монотонно неубывающей независимо от знака у, так что в случае a' > a будет G_y(a',U ) > G_y(a,U ) и B_y(a',U ) ^ B_y(a,U ), причем последнее неравенство выполняется строго, если b(r) >  0 для некоторого г G (a, О). Кроме того, как интегралы от непрерывных кусочно-гладких функций все они являются гладкими, вторые производные которых кусочно-непрерывны.

Схема решения поставленной задачи следующая. Сначала при фиксированных значениях Т и U исследуется влияние вариаций избыточной смертности v (а) на функции (17) -(20). Устанавливаются запрети! и допустимые вариации v (а) в случае оптималвных с точки зрения задачи (15) значений параметров. Следующим шагом является выявление допустимых с точки зрения оптималвности значений для Т при условии допустимости для v(а). Завершающим этапом служит выявление допустимых значений U при условии допустимости для v(а) л Т.

• 5.    Учет вариаций избыточной смертности

Пусть известны U. Т ii v(а). Фиксируем некогорое положительное £ ^Т. Для |А| ^ 1 я г G (0, Т — £) будем задавать игольчатые вариации избыточной смертности v(а) в виде ^д(а,г) = у д(а — г)д(г + £ — а) ^ 0, г де 6(h) = {0, h С 0; 1, h > 0} - функция Хевисайда, так т что I 6у(а,г)dа = А. Функцию, построенную из /(а) путем замены v(а) iia. v(а) + ду(а,г). 0

мы будем обозначать как /у(а,г). Второй аргумент г здесь указывает на место приложения игольчатой вариации ду(а,г) к избыточной смертности v(а), так что, например, vд(а, г) = v(а) + 5д(а, г). Во избежание индексных нагромождений мы здесь опускаем ряд используемых в других местах и считающихся здесь постоянными аргументов, так что р(а) = рц (а,и). F (а) = F, (а,и). С(а) = G, (а,и). В (а) = В, (а,и). В силу малости интервала (г, г + е) мы также будем опускать достаточно просто вычисляемые, но несущественные с точки зрения последующих результатов, значения функций /у(а,г) на нем, ограничиваясь лишь значениями на интервалах (0,г) и (г + £,Т).

Теорема 2. С точностью до о(А) выполнены следующие равенства ру(а, г) = {р(а), а < г; р(а) + А,а> г + е},(21)

F^o, г) = {F (а),а < г; F (а)(1 — А),а > г + е},(22)

Ga(o, г) = {G(o), а < г; G(o) — А(G(а) — G(г)), а > г + е},(23)

Ву(а, г) = {В(а), а < г; В(а) — А(В(а) — В(г)), а > г + е}.(24)

т

Доказательство. (21) - это следствие из (17) и равенства / 5 у (а,г)да = А. Из (18) 0 находим

F A (а,г) — F(а) = е^-^^ — е^-р(а) = е ^{- р(а} ( е^-^’^ — 1) - —F(а)(р у (а,г) — р(а)) откуда, заменяя здесь и далее знак приближенного равенства на точное, получаем с учетом (21) равенство (22). а                          а

Далее. GA(а,г) — G(а) = J (FA(s,r) — F (s))ds = J (Fyfar^—F (s))ds. так что для а > г+е а будет Ga^v) — G(o) = —А [ F(s)ds, откуда с учетом (22) получаем (23). а                                    а

Аналогично Ву(а,г) — В(а) = \ b(s)(FA(s,г) — F(s))ds = —А ( b(s)F(s)ds для а > г + е. 0                                         г что в совокупности с (22) дает (24).

• 6.    Оптимальная избыточная смертность

Пусть известны оптимальные значения U, Т и v(а). Необходимым условием оптимальности v (а) при неизменных U иТ является с учетом (13) и (14) неравенство

В и (Т,и) ^ В, ‘ (Т,и )

при условии выполнения равенства

G y (Т , U ) = G y ‘ (Т , U ),

для любви v‘ = v‘(а). Будем искатв v‘ в виде v ‘(а) = v (а) + 6д1 (а, ri) + 6д2 (а,^

с |А1,2| ^ 1, е < r_i + £ < г₂< Т — е, 0 < е ^ Т. Обозначим v 1 = v 1 (а) = v(а) + 6д1 (а, г 1 ), так что v' = v ‘ (а) = v₁(а) + 6д₂ (а,г 2 ). Положим также G 1,2 = G_y(r 1,2 , U ), G t = G_y(Т, U ), G¹(а) = G y 1 (а,и\ G 2 = G¹^). G T = G ¹ (Т ). G'(а) = G_y ‘ (а,U ). G'_t = G'(Т). В силу (23) имеем G¹(а) = G(а) + Ai(Gi — G(а)) щш а > ri + е. так что

^G 2 = ^G 2 + ^A 1 ^(G 1 - ^G 2 )

и

GT = Gt + A1(G1 — Gt ).(29)

Аналогично G'(а) = G1(а) + A2(G2 — G1(а)) при а > Г2 + е (ибо для таких а функция Gv‘ (а,и) представляет собой возмущение для G1(a) посредством чамеив! V1(а) на. v'(а) = v1(а) + 6д2(а, r2)). так что gt = gT + A2(g2 — gT ).(30)

Подставляя (28) и (29) в (30), находим

G_T — G t = A_x(G i — G t )+

+A2(G2 + Ai(Gi — G2) — (Gt + Ai(Gi — Gt ))) =(31)

= (Ai(G i — G t ) + A 2 (G 2 — G t )) + A±A 2 ( G t — G 2 ).

Условие (26) - это равенство G t — G t = 0, так что для |Ai,2| ^ 0 из (31) находим необходимое условие для его выполнения:

A i

G t — G 2

-

G t — G i

A 2

Заметим, что в силу положителвности левой части в (32) sign Ai = —sign A2.

Аналогично для В 1, ₂ = B y (r 1, ₂,U ), B_T = B y (Т,и ), B'_T = B y ’ (Т,и ), используя вместо соотношения (23) равенство (24), находим вместо (31)

BT — Bt = (Ai(Bi — Bt ) + A2(B2 — Bt )) + AiA2(Bt — B2), так что при |Ai,2| ^ 0 c учетом (25), (32) имеем необходимое условие оптимальности по v(а) при (фиксированных U и Т вида.

0 > A i (B i — B t ) + A 2 (B 2 — B t ) =

= ^A 2 [ Д 2 ^(B i — ^B T ) ^{+ (B} 2 ^{— B} T )] =

= A 2 [— ^^ (B i — B t ) + (B 2 — B t )] =

= A₂(G_t — G₂) [ ^-^ — ^-^2] .

^ T — ^1    ^ T — ^2

Заметим, что поскольку выражение в (33) симметрично относительно перестановки индексов 1 о 2, то с учетом сделанных предположений о малости е и Ai,2 условие е < r i + е < Г 2 < Т — е можно ослабить до r i2 G (0, Т ) с ri = Г 2.

Поскольку функция Gy(а, U) является строго монотонно возрастающей по а, то определена обратная функция ay(д, U), такая что ay(Gy(а, U),U) = а.

При этом, поскольку в силу (19) ^(^^~ = Fv(°, U)> то Для обратной функции выполнено неравенство

доДдДи) ₌    1

дд       Fv (a,U)    ’ так что функция av(g,U) является гладкой. Положим

Pv (g,U)—Bv (av (g,U),U ).

Содержательный смысл функции 0v(g, U) при фиксированных и и U ~ это биологический потенциал младшей части популяции, для которой число особей в расчете на одного новорожденного равно g. Мы будем называть ее плотностным профилем биологического потенциала. Заметим, что функция 0v(g,U) как суперпозиция гладкой и кусочно-гладкой является также кусочно-гладкой.

Обозначим

Д (U,U ) -Pv (g,U )

^{U -} g

^v ⁽g^,U )

И

Bv (T,U ) -Bv(а,и )

^{Фv (}a, ^U ) - < ⁽G^v(a, ^U)U ) - _Gv(T, U ) — _Gv(°, u )

Теорема 3. Для оптимального и (а) при фиксированных U иТ неравенство и (r_i,₂) >  0, выполненное для некоторых 0 < r1 < r₂< Т, влечет

Ф v (ri,U )-Фv (r2,U).                                (39)

Доказательство. В указанном случае при возмущении вида и ‘(а) из (27) А2 может быть произвольного знака, так что последнее выражение в квадратных скобках в (33) должно обращаться в нуль.

Теорема 4. Для оптимального и (а) при фиксированных U иТ выполнение для некоторых r1,₂ G (0, Т) , r_i — r₂ равенства и (r_i) — 0 и неравенства и(r₂) >  0 влечет неравенство

Фv(ri,U) > Фv (r₂,U).                                   (40)

Доказательство. В указанном случае при возмущении вида и ‘(а) из (27) должно быть А1 >  0, так что в силу (32) А2 <  0. Отсюда следует неотрицательность последнего выражения в квадратных скобках в (33).

Теорема 5. Если для оптимального и (а) при фиксированных U и Т найдется r1 G (0,Т) такое, что и (r_i) >  0. то множсство r таких, что и(r) >  0. включает в себя некоторый непустой интервал, содержащий r1 в своем замыкании. При этом для некоторого q G [0, U ^-1] njхи p — 1 — qU для всех таких r для g — G_v (r, U ) будет выполнено равенство

Д ⁽g^{,U )—} p + qg,                               (41)

а для тех r'. для которых и (r') — 0. д.чя g' — G_v(r',U ) - неравенство

Д⁽g', ^U ) <  p + q^g.                                 (42)

Доказательство. При выполнении неравенства и (ri) >  0 для некоторого ri G (0, Т) в силу кусочной непрерывности и(r) >  0 на интервале (0, Т ) найдется еще одно r2 — ri, такое, что и(r) >  0 на интервале между ri и r2. Из (39) следует, что для них будут выполнены равенства Ф_v (r1,₂,U ) — q — const с некоторым q ^ 0. В силу (38) для g1,₂ — G_v(r1,₂,U ) с gi — g2 отсюда получаем Д(gi,2,U ) — q. так что для Д,₂ — Pv(gi,2,U ). Дц — Pv(U,U ) при i — 1,2 будет Дц - Д — q(U — gi) и q может быть вычислено из соотношения 02-Pi — q(g2 -gi)- Пр;шая 1(g) — Дц - q(U-g) — p + qg включает обе точки (gi, Д). i — 1, 2. на плоскости (g,0). Этой же прямой принадлежит и точка (и,Дц ). посюхтьку l(U ) — Дц. Нулевому возрасту а — 0 соответствуют значения go — G_v(0,U ) — 0 и До — 0_v(go,U ) — 0

(с учетом непрерывности можно говорить не о нулевых, а о сколь угодно близких к нулю положительных величинах), так что с учетом (37) - (39) и (40) получаем неравенство ^ = ^ и - д ⁰ fl ^ и - д ¹ = ^’ ^и> следовательно, р = fl u — qU fl 0, откуда, принимая во внимание условия стационарности fl u = 1 (см. (16), (14), (36)), получаем неравенство q <  U ^-1.

В силу (39) прямая 1(g) включает в себя все точки плоскости (g,fl) с fl = fl_y(g,U ), д = G_y(г, U ), для которых v(г) >  0, так что для них выполнено равенство (41). В случае же v(г') = 0 при v(ri) > 0 для пекоторого ri е (0,Т) в силу (40) для fl' = fl_y(g',U ) выполнено неравенство ^и—д г fl ^ и-д = У- ^откУДа следует неравенство fl ' ^ fl u — q(U — д') = р + qg '. т.е. (42), которое означает расположение точки (g¹ ,fl ') не выше прямой 1(g).

Теорема 6. Для g е (0, U ) выполнены равенства

" '^0gJ' = b(a y (g,U)),                                (43)

dg

а в точках гладкости функции b(a) для g = G_y(a, U ) - равенство

. д^Д ⁽ g ^,U )

^Sign dg?

= sign д=С , (a,U )

db(a) da ’

Доказательство. Дифференцируя (36) по g, имеем

При этом, поскольку в силу (20) при всех a

ДДдД _ дД дд е (0,Т)

ДОДД I да    \а=а„ (д,и)

даДди) дд

*

выполнено равенство

^дВ‘' да, ^и ) = b(a)F_y(a,U ). то равенство (35) влечет (43). Дифференцирование (43) по g в

точках гладкости функции b(a_y (g, U )) дает венства (35) получаем (44).

& 2 Ц у (g,U )    дЬ(а) да „ (g,U )

дд ²

да дд

, откуда с учетом нера-

Назовем кусочно-гладкую функцию рождаемости b(a) стандартной, если из b(a) = С для a е (ai,a2) С (0,Т) с ai = a2 следует С = 0. Назовем возрастной интервал (Ть,Т ). ap е (0,Т). финальным интервалом станнартной функции рождаемости b(a). если Ть = sup{a : b(a) >  0} < от. Содержательный смысл стандартной функции рождаемости заключается в том, что она не может быть постоянной на каком-либо возрастном интервале, за исключением случая, когда она там нулевая. Для такой функции рождаемости финальный интервал составляют все старшие возраста, после которых рождаемость отсутствует. Назовем избыточную смертность v (a) fl 0 для стандартной функции рождаемости допустимой, если она равна нулю везде, кроме, быть может, финального интервала.

Теорема 7. Для стандартной функции рождаемости b(a) оптимальная избыточная смертность v (a) является допустимой.

Доказательство. Пусть v (ri) >  0 для некоторого ri е (0,Т). В силу теоремы 5 тогда v (a) >  0 на некотором непустом интервале, содержащем ri в своем замыкании и еще некоторое Г2 = ri. В силу теорем 5 и 6 на этом интервале ^а) = 0, так что для стандартной функции рождаемости на нем было бы b(a) = 0, а значит, и на всем интервале между ri и r2. Если бы для некоторого гз е ( г 1 ,Т ) был о бы Ь(гз) >  0, то в силу непрерывности функции b(a) с учетом (18) получили бы (см. (20)) неравенство •Г3

Bi(r3,U) — Bi(ri,U) = J' b(s)Fy(s,U)ds > 0. так что в силу монотонного неубывания функ- щш B(a) выполнялись бы соотношения By(Т,U) — By(ri,U) = By(Т,U) — By(r2,U) > 0. откуда с учетом неравенства Gy(ri,U) = Gy(r2,U) в силу (38) следовало бы неравенство Ф^(ri,U) = Фу(r2,U). противоречащее (39).

Теорема 8. Для стандартной функции рождаемости b(a) допустимая избыточная смертность v(a) е> случае: сохранения относительной численности U нс меняет плотностный профиль биологического потенциала, т.е. fl_y(g,U ) = flo(g,U ).

Доказательство для a ^ Т ь следует из (34), (36) и очевидных равенств: G_y(a,U )  = G₀(a,U ) ii B y (a,U ) =   B₀(a,U ). Для a >  Т_ь ii з b(a) = 0 следует

By(a,U) = By(Тb,U) = B0(Тb,U) = B0(a,U) для лтобого a' > Ть. а стало быть, ii fly (g, U) = fly (Gy (a, U ),U) = flo (Go(a', U), U) д, тя a = ay (g, U) ii a' = a0(g, U).

Заметим, что равенство (13) при условии сохранения относителвной численности U, обеспечивающем сохранение плотностного профиля биологического потенциала, означает выполнение равенства G o ( T,U ) = G „ (Т ' ,U ) для некоторого Т ‘ > Т ^ Т ь в случае, если v (а) > 0 для некоторого a G (Т ь ,Т ). Другими словами, предельный возраст при наличии ненулевой допустимой избыточной смертности v (а) должен увеличиваться, подстраиваясь под сохранение относительной численности. При этом вид самой функции v (а) при а ^ Т ь значения не имеет.

Это верно для любого плотностного профиля, в том числе и для получаемого в случае, когда избыточная смертность оптимальна. В последнем случае указанное подстраивание снимает вопрос об оптимальном предельном возрасте Т, оставляя в качестве единственного параметра, по которому осуществляется оптимизация, относительную численность U.

Совсем другая картина наблюдается, когда Т < Ть. В этом случае оптимальная избыточная смертность нулевая и оптимизация производится по обоим параметрам Т и U.

• 7.    Оптимальные относительная численность и продолжительность жизни

Пусть b(a) - стандартная функция рождаемости. В случае оптимальных U п Т < Ть в силу теоремы 7 оптимальная избыточная смертность равна нулю при a G (0,Т). Случай Т ^ Ть, уже разобранный выше для v (а) ^ 0 пр и а ^ Ть (см. теорему 8 и конец предыдущего раздела), также не исключается в настоящем разделе в варианте v(a) = 0. Это позволяет построить вариации для G^ (T,U) и В„(T,U) при изменении Т и U, ограничиваясь рассмотрением только функций Go(T,U) и Bo(T,U). Обозначим т'(U,a') = ^^д^), а p(U,a') = р0дц’а) = ] т'(U, s)ds. см. (17).

Теорема 9. Пусть Т u U связаны соотношением (13) при v(а) = 0. При выполнении условий их оптимальности для Во(Т, U ) должно выполняться равенство

т

У b(a)F(а)р(U,a')da. о

b(T ) I 1 + / F(a')P(U,a)da \     'о

Доказательство. Пусть заданы связанные соотношением (13) вариации Т ^ Т_т = Т+т я U ^ U_v = U + v с• |т| ^ Т 11 |v| ^ U. Из (17) - (20) с учетом v(а) = 0. пренебрегая малыми высшего порядка по т и v, получаем для соответствующих вариаций следующие выражения (поскольку здесь везде v (а) = 0, то нижний индекс имеет иное значение, чем это было раньше, так что, например, B(U, а) = B o ( U, а), где справа стоит использовавшееся ранее (см. (17)) обозначение):

m(Uv, а) = m(U, а) + т'(U,a')v,рv(U,a')= [ m(Uv,s)ds = р(U,a')+ vp(U,a'),

о

Fv(U, а) = exp(—pv(U, а)) = exp (—p(U, а) — vp(U, а) = F(U, а) (1 — vp(U, а) ,(46)

Gv(U, а) = У Fv(U, s)ds = У F(U, s) (1 — vp'(U, s) ds = G(U, а) —v] F(U, s)p(U, s)ds, ооо

Bv(U, а) = I b(s)Fv(U, s)ds = B(U, а) —v] b(s)F(U, s)p(U, s)ds,(48)

оо

Из (46), (47) находим

G_v(U, Т_т ) = / F_v(U, s)ds = G_v(U, T ) + '/ F_v(U, s)ds = о                           T

T

= G(U, T) - vf F(U, s)p'(U, s)ds + tF(U, T) (1 - vp'(U, T)), а из (46), (48) с учетом непрерывности b(a) пр и a = T

Bv(U,Tt) = J b(s)Fv(U,s)ds = Bv(U,T) + J b(s)Fv(U,s)ds = t 0                               T                              (30)

= B(U, T) -v f b(s)F(U, s)p'(U, s)ds + Tb(T)F(U, T ) (1 - vp ' (U, T )) .

Соотношение (13), выполненное как для U, так и для U_v, вместе с (49) влечет равенство т

Uv = U + v = Gv(U,Tt) = G(U,T) -v/F(U,s)p(U,s)ds + tF(U,T)(1 -vp(U,T)), из которого вв1текает соотношение пропорциональности между малыми отклонениями т и v:

v I 1 + У F(U, s)p ' (U, s)ds I = tF (U,T). 0

Подставляя (51) в (50), получаем вариацию для биологического потенциала B(U,T ):

B_v ( U,T t ) -B(U,T ) = v

b(T) I 1 + У F(U, s)p ' (U, s)ds 0

-

т                   \

I b(s)F(U,s)P(U,s)ds I .

Неравенство B_v ( U,T _t ) ^ B(U,T) является необходимым условием оптимальности B o (T, U ). так что в силу произволвности выбора знака отклонения v множителв при нем должен обращатвся в нуль, т.е. должно выполняться равенство (45).

При параметризации

m(U, a) = М(U)Y(a) + у,                            (52)

соответствующей разделению сомножителей после поправки на сдвиг с постоянной у = const, определяющий экспоненциальные изменения, соотношение (45) с учетом (17) при v(a) = 0 принимает вид

b(T )

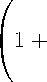
т

М '(U )

_М ( _U ) J ^{F ( a ) (}P o ^{( U,} a) ^- У ^{a ) da}

т

М' (U )

_М ( _U ) I ^{b ( a ) F ( a )} (Po^ ^{a ) -} У ^{a ) da}

Пусть теперь функция М(U) унимодальна, так что — ^^ ) >  0 и для некоторого U * > 0 dM ( U *)

выполнено равенство — фи = 0.

Теорема 10. В условиях теоремы 9 в случае параметризации (52) с унимодальной функцией М(U) при рождаемости b(a) = 0 на интервале a G (0, T) в случае b(T) = 0 оптимальное значение для U равно U *.

Доказательство. Из (51) следует, что в случае b(T) = 0 будет М'(U) = 0, если только интеграл в правой части (51) не обращается в нуль. Избавиться от такого обращения в случае необходимости можно, подставив на место у элементы монотонной последовательности yk ^ у - 0 с тем, чтобы указанный интеграл оставался положительным. Его отклонение от нуля в условиях следствия, касающихся функции рождаемости, будет порядка Се^ с Ek = у - yk > 0 и некоторой постоянной С > 0, не зависящей от к, так что соответствующее изменение верхнего предела интегрирования, имеющее такой же порядок, с учетом харак тера изменения подынтегрального выражения на положительность интеграла не повлияет. Поскольку предел оптимальных значений является оптимальным (имеется в виду выполнение соответствующих нестрогих неравенств), а таковым при каждом у^ для U является U*. то оно же будет оптимальным и для предельного 'значения у.

Замечание. В биологической интерпретации приведенный в теореме 10 результат означает, что при равной нулю избыточной смертности оптимальная продолжительность жизни должна быть такой, чтобы величина относительной численности, достигаемая за отведенный срок, обеспечивала минимум обусловленной этой величиной смертности.

В случае Т > Тъ в силу теоремы 8 допустимая избыточная смертность не меняет плотностного профиля биологического потенциала, что позволяет достигнуть значения U* за счет подходяще выбранного v(а) > 0 для a > Тъ, если, конечно, U* достаточно велико, несколько позже, чем в случае v(а) = 0, т.е. при некотором Т' > Т, где Т вычисляется из соотношения (13) при v(а) = 0 и U = U*. В этом случае соотношение (53) выполняется автоматически и вычислительного интереса не представляет.

Совсем иная ситуация имеет место при Т < Тъ- Согласно формуле (53) в этом случае максимальная продолжительность жизни Т представляет собой возраст, при котором рождаемость не обязана быть равной нулю, а всего лишь несколь ко меньше средней рождаемости, вычисленной с возрастной весовой функцией вида

( М (U ){Y (s^

F(a)(p₀(U,a) — уа) = F(а)

> 0, где U и Т снова связаны соотноше нием (13). Параметр у подбирается при этом таким образом, чтобы для биологического потенциала из (20) выполнялось соотношение Во(Т, U) = 1. Поскольку в случае параметризации (52) весовая функция положительна, то при выполнении неравенства М'(U) > 0 из (53) получаем неравенство Ь(Т) > 0. Этот результат означает, что на участке роста М(U) оптимальность биологического потенциала (20) влечет в качестве следствия отсече ние у жизнеспособных популяций части старших возрастов даже в случае фертильности последних. Тот же эффект наблюдается и в общем случае, т.е. без параметризации (52). Вместо нее достаточно потребовать, чтобы для всех а G [0,Т] выполнялось неравенство p'(U, а) ^ 0, причем для некоторого а, такого что Ь(а) > 0, выполнялось неравенство т'(U,a') > 0. Содержательный смысл последних условий такой. Прирост относительной численности популяции может влиять на взвешенный рост смертности только в сторону ее возможного увеличения для каждого значения возраста в группах, возраст в которых не превосходит заданного значения, причем для некоторого фертильного возраста такое влияние является ненулевым.

Результаты расчетов мы продемонстрируем на следующем примере. В (52) применялись следующие параметризации: у = 0, М(U ) = 0.3U +1, Y(а) = 2а + 1. Функция рождаемости имела вид трапеции: Ь(а) = max(0, min (3.135, 60 (а — 0.1) , 7.5(1 — а))), так что Т ъ = 1. Расчеты по формулам (13) и (53) в случае В = 1 выдали следующие значения: U = 0.47 и Т = 0.9688.

То, что Т < Тъ, - это общее свойство и для всех других проводившихся численных экспериментов. Оно допускает вполне объяснимую биологическую интерпретацию: если имеет место возрастание смертности с увеличением относительной численности популяции, то в ней происходит «отрезание по-живому», т.е. исчезают не только старшие нефертильные возраста, но и некоторые, близкие к таковым, фертильные.

• 8.    Выводы

В рамках модели Лотки со смертностью, зависящей от суммарной численности популяции, принцип эволюционной оптимальности не дает ответа на вопрос об эволюционных преимуществах избыточной смертности и ограниченности индивидуальной продолжительности жизни. Механизмы внутрипопуляционной регуляции численности демонстрируют, как правило, полное безразличие по отношению к возможности самоликвидации особей, вышедших за пределы фертильного периода. Более того, гипотетическая возможность бесконечности такого периода делает популяцию потенциально бессмертной. Здесь, правда, проявляется «парадокс бессмертия», заключающийся в том, что такие популяции оказываются ненаблюдаемыми в природе.

В случае зависимости смертности от относительной по отношению к числу новорожденных численности проявление обозначенного безразличия наблюдается в случае функций рождаемости стандартного типа, наиболее характерных для реальных популяций. Однако для зависимости указанного типа ключевым регулирующим фактором оказывается указанная относительная численность. В случае, если таковая становится на каких-то значениях оптимальной, то остальные параметры подстраиваются в процессе эволюции под эти значения. Подстраивание происходит также и в случае, когда имеет место монотонное возрастание смертности с ростом относительной численности. В этом случае вполне естественным оказывается «отрезание по-живому», т.е. сокращение максимальной продолжительности жизни до возрастов, меньших, чем возраст окончания фертильного периода.

Автор выражает глубокую благодарность А. И. Лобанову за ряд полезных замечаний.