Применение теории потенциала при численном решении обратной задачи гравиметрии

Важнейшее место в гравиметрии занима-ет задача аналитического продолжения за-данных значений поля на поверхности Зем-ли в нижнее (верхнее) полупространство . Вопросами аналитического продолжения, определения особых точек гравитационных полей занимались такие ученые, как Т.М. Воскобойников, А.А. Логачев, В.И. Андреев,В.м. Березкин и многие дру-гие .В.Н. Страховым был предложен подход по аналитическому продолжению значений, в основе которого лежит разработанный им метод дискретных аппроксимаций физиче-ских полей (Страхов, Арсанукаев, 2002). Реализация этого подхода с использованием соответствующих дискретных схем связана с заменой вторых частных производных дифференциального оператора уравнения Лапласа вторыми разделенными разностя-ми ; непрерывные функции заменяются се-точными функциями. В результате задача аналитического продолжения заданных зна-чений гравитационного поля в нижнее по-лупространство с использованием уравне-ния Лапласа сводится к задаче составления и решения систем линейных алгебраических уравнений . Указанный подход был использо-ван при проведении целого ряда вычисли-тельных экспериментов по аналитическому продолжению для гравитирующих тел с раз-личными формой поверхности и плотностью (Арсанукаев, 2013, 2015, 2016, 2017). Была разработана специальная методика оценки точности расчетных значений гравитацион-НОГО ПОЛЯ, получаемых в нижнем полупро-странстве по заданным значениям; системы линейных алгебраических уравнений (СЛАУ), возникающие при решении задачи аналитического продолжения, решались ме-тодом простой итерации. Следует отметить, что задача аналитического продолжения, Ре -шение которой приведено выше, является не-корректно поставленной в смысле классиче-ской постановки задачи Дирихле для уравне-ния Лапласа в прямоугольнике. Действитель-НО , заданные значения, определяемые на практике по результатам гравиметрической съемки, располагаются только на части кон-тура (в отличии от классической постановки), имеющего форму прямоугольника, обычно на дневной поверхности Земли. Тем не менее были получены вполне удовлетворительные

результаты при аналитическом продолже-НИИ , когда заданные значения поля распола-гались на уровнях (профилях): на уровне Земли : z = 0 и на уровне шага сетки выше уровня Земли : z =-h (ОСЬ Oz направлена вниз). По результатам аналитического про-должения уверенно определяются верхняя кромка области, заполненной тяготеющими массами, особые точки (при наличии), центр тяжести области и с меньшей точностью положение нижней кромки области .

Следующим шагом в решении обратной задачи гравиметрии, после определения на первом шаге контура области, заполненной массами, может быть определение плотно -сти масс также в результате аналитического продолжения , но теперь внутри области, занятой массами . Заданными значениями по всему контуру области при аналитическом продолжении будут являться значения гра-витационного поля, полученные на первом шаге , как указано выше . Но при аналитиче -ском продолжении внутри области, запол-ненной массами, очевидно , предварительно необходимо решить две основные пробле-МЫ . Во-первых, известная формула Пуассо-на, описывающая поле гравитационного по-тенциала внутри масс , здесь непригодна, поскольку при решении задачи аналитиче-ского продолжения на первом шаге с помо-щью уравнения Лапласа, описывающего по-ле гравитационного потенциала (и его про -изводных) вне масс, заданными значениями являются значения вертикального градиента потенциала (аномалия силы тяжести Aq , -лученная в результате гравиметрической съемки); соответственно , «входные » значе-ния поля, которые будут использованы при аналитическом продолжении уже внутри масс , будут значениями поля первой произ-водной потенциала (а не просто потенциа-ла). Во- вторых , для существования решения необходимо, чтобы поле первой производ-ной потенциала было непрерывным во всем пространстве ‒ как внутри масс, так и вне масс .

Остановимся на этих вопросах подробнее (Идельсон, 1932; Sternberg 1974; MacMillan, 1930).

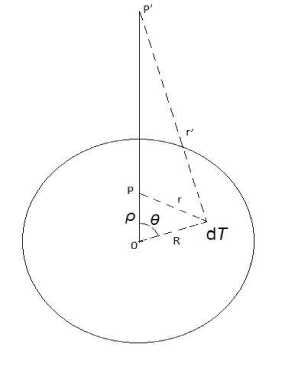
Рис. 1. Однородная сфера

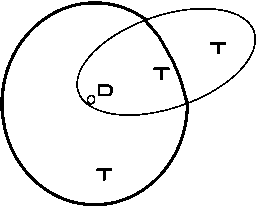
Рис. 2. Тело переменной плотности

Потенциал ее на точку наблюдения P есть m = Jr ^ ,      (1)

где интегрирование распространено на весь объем сферы Т. Для выполнения квадратур возьмем систему полярных координат с нача-лом в центре сферы и направим полярную ось на точку наблюдения Р (рис. 1). Смотря по тому , будет ли лежать она внутри сферы или вне ее (в Р'), у нас будет р < R или же р > R . Но во всех случаях расстояние r от Р до пере-менного элемента dZ. объема определится по формуле г² = р² + й² — 2pRZ 11^ (2).

y( p)_ j j j ^^ sinOdfM(pdR . (4) oo v^p² +R² —2RpcosO

Интеграл (4) вычисляется в квадратурах с :

а) р > R, т.е. притяжение на внешнюю точку Р .                                  :

V(P' )= ^й³-

'  ⁷ з р

Но -тгй есть масса всей сферы М ,

:

V{P^! ) =7 .          (5)

Таким образом , потенциал всей сферы свелся здесь к точечному потенциалу : -родная сфера притягивает внешнюю точку так , как если бы вся ее масса была сосредо-точена в ее центре . Этот результат легко распространяется на случай сферы, СОСТОЯ-щей из однородных концентрационных ело-ев . Такая сфера тоже притягивает внешнюю точку так, как если бы вся масса была со-средоточена в ее центре .

б) р < R ,т.е. притяжение на внутрен-нюю точку P. Теперь потенциал

V(P) = 2np(R² -^-)   (6)

равен (6). Вводя в эту формулу массу сферы о 2   ЗМ

М,т.е. полагая К =---, можем перепи- сать предыдущее выражение в виде т=^а-^>.   (7)

Из формул (5), (6), (7) вытекает ряд важ-ных следствий , :

• 1)    Потенциал однородной сферы есть функция , ограниченная и непрерывная во всем пространстве : , и вне ее , в точках Р поверхности сферы,т.е. при р = R обе формулы (5) И (7) дают

V(P)~

.

• 2)    Потенциал достигает своего максималь-ного значения внутри сферы, именно в ее центре ( р = 0 ), где он равен

V(Q )=^ЗМ = 2npR² .       (8)

2 R

От этого максимального значения потен-циал V(P) непрерывно убывает и при р -t ж стремится к нулю . Причем характер измене-ния потенциала как функции р внутри сферы носит параболический характер, вне сферы он убывает по гиперболическому закону .

• 3)    Первые производные потенциала одно-родной сферы являются функциями, ограни-ченными и непрерывными во всем простран-стве ;              :

(внутри массы; р < R ) (9)

(вне массы; р > R ). (9а)

На границе, при р = R обе формулы дают ^ = _МР- дК _ М др R3 др ” R2        (10)

^L=_^L др р2 .

• 4)    Потенциал V(P) как функция координат точки Р удовлетворяет вне сферы уравнению Лапласа :        ; внутри сферы он удовле-

• творяет уравнению

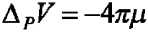
Справедливость первой части следствиям можно установить непосредственным диффе-ренцированием ; для доказательства второй достаточно заметить, что внутри сферы по-тенциал ввиду (6)      :

V( Р)=const-^р¹ = Const-^(Е? +1? +^²9

, но д^) d^f) д^) = д^2 dq2 д^2

и поэтому действительно

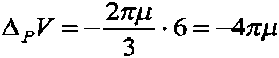
Уравнение (11) носит название уравнения Пуассона; мы заключаем теперь, что уравнение Лапласа есть только его частный слу-чай: вне сферы д = 0, так что уравнение Пуассона переходит в уравнение Лапласа, и мы можем сказать, что потенциал V удовлетворяет во всем пространстве уравнению

\PV = -4лр.

Полученные результаты для потенциала однородной сферы нетрудно перенести на случай произвольного распределения объ-емных масс с переменной плотностью. Начнем с доказательства справедливости следующего утверждения:

Потенциал любого объема и на любую

, -

.

Пусть Т есть данный объем, Р - точка внутри его. Опишем вокруг Р сферу, объем которой был бы равен Р ; пусть R - ее радиус (рис. 2).

Тогда объем Т распадется на части 11 (внутри сферы) и 22 (вне ее). Обозначим через Тз ту часть объема сферы, которая лежит вне Р; очевидно Тз = Т2. Допустим теперь, что тело однородно и плотность его равна 1. Тогда потенциал Т на Р = dr

,dz ,dt

J •■ J , а потенциал сферы на Р =

?i Т₂ Г

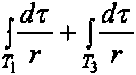
Покажем сейчас, что

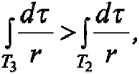
откуда и будет следовать, что потенциал сферы больше по тенциала объема Р. Для этого достаточно заметить, что

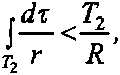
так как расстояния элементов объема Р 2

до Р больше R, и что, так как расстояния элементов Тз до Р меньше R, 3з = 7г и

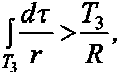
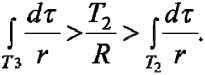
Нетрудно привести доказательство и для случая, когда Р находится вне Р; потенциал и здесь меньше 2л^², где R - радиус сферы, объем которой равен Р . Наконец, если тело Р неоднородно, то плотность его, которую мы должны считать ограниченной, будет меньше некоторого максимального значения р '; в этом случае потенциал Р на любую точку Р меньше, чем 2лр 'R², где R есть радиус сферы, объем которого равен Т.

Из доказанного положения следует, что потенциал объемных масс есть функция, ограниченная во всем пространстве , иными словами, г pd\Z

J^ ^есть интеграл всегда сходящийся, несмотря на нуль, который появляется в знаменателе , когда Р находится внутри Р\ более того, отсюда вытекает, что объемный -отен--странстве ; он не терпит разрыва, когда Р переходит из данной массы во внешнее про -странство; чтобы убедиться в этом, достаточно вырезать из Р объем Р, заключающий Р, тогда потенциал остальных масс есть функ-ция непрерывная, где бы ни лежала точка Р внутри Р'; но потенциал Р' на Р меньше 2тщР², где R - радиус сферы, объем которой равен Р'; при R—»0 этот потенциал идет, очевидно , к нулю.

Аналогично случаю объемного потенциала можно показать, что первая производная объемного потенциала есть функция координат, ограниченная и непрерывная во всем про -

.

Для объемного потенциала справедлива теорема Пуассона, как и для однородной сферы в следующей форме: Во всех внутренних

T             V(p)            - ряет уравнению

A^(H = -4^mW, где р(Р) означает плотность в точке P.

Для доказательства, следуя Грину , выде-лим внутри объема Т сферу X, окружаю-щую Р, при этом потенциал всего тела Т на Р разобьется тогда на две части; одна из них (V"), будет зависеть от масс , лежащих вне сферы :        (V') ‒ от масс, находящихся внутри ее . Если теперь неограниченно уменьшать размеры сферу, ее можно было бы считать однородной с плотностью той же , что и в лежащей внутри сферы точке Р, так что в пределе получим при V' —>V ^p(^) = -^^('p,) , как для потенциала V однородной сферы (V" как потенциал масс, лежащих вне сферы, будет удовлетворять уравнению Лапласа).

И наконец выведем результат , ЯВЛЯЮ - щийся обобщением формулы Пуассона (11) для поля производной объемного потенциа-ла внутри притягивающих масс . Вначале найдем производную потенциала

V(P)^lnp(R²-^) , равную ^— = 3             vp

-ZW . Затем продифференцируем

:

р =	:^2+П2+С2 ;
sp		д^р_	1	11
			^^— ——
	р’	зГ	р	р3 ;
др	п .	сРр _	1	п2
^^—^^	-		^^_ -
дг}	р’	дтр	р	р3
др		д^р _	1	_£1
^^^^^	^^—		— ----- —
дС	р'	^2'	р	р3

Складывая полученные вторые произ- водные и умножая на —^ггг ,        :

AfdV\    4   /

^ )= "^( р р3

) = — |д(" “ ”) = з ^р р

- “Д^

т.е. окончательно с )=" Зр^ .      (13)

В связи с вышеизложенным, определение распределения плотности внутри гравитиру-ющих масс будет происходить в следующей :

• 1)    значения поля Aq ,                    -

• тате проведения гравиметрической съемки на поверхности Земли, пересчитываются на за-данные горизонтальные уровни z = -h, z = 0 (ось Oz направлена вниз) в узлы равномерной сетки с заданным шагом ;

• 2)    полученные в п . 1 значения поля на за-данных горизонтальных уровнях в узлах рав-номерной сетки используются в качестве «входных» значений при решении задачи аналитического продолжения (восстановле-ния) значений поля вокруг источника поля с использованием дискретных аппроксимаций оператора Лапласа; по найденным в результа-те аналитического продолжения значениям поля в нижнем полупространстве определяет-ся контур области, заполненной тяготеющи-ми массами;

• 3)    восстановленные в п . 2 на границе ис-точника значения поля используются в каче-стве «входных» значений при решении урав-нения Пуассона в его обобщенной форме (13) внутри притягивающих масс , поскольку по-тенциал объемных масс (и его первые произ-водные), как показано выше , является всюду непрерывной функцией и его значения (И первых его производных) вне масс и внутри масс совпадают в точках поверхности огра-ничивающей массы. Данная технология была реализована в условиях модельного примера вертикального пласта, имеющего размеры 4.8х4.0 км в плоскости О xz однородной плот-ности с ц=9.2г/см³ и бесконечной протя-женности в направлении оси у,т.е. в условиях двумерной задачи (рис. 3).

874.(13)

Таким образом, здесь решается задача : «входным » значениям поля, заданным по всему контуру прямого пласта с использова-нием дискретных аппроксимаций уравнения (13) восстановить значения поля вертикаль-ного градиента потенциала и значения сеточ-ных масс (плотностей) внутри прямого пла-ста . Вводя внутри прямого пласта равномер-ную сетку с шагом h=0,2 км , получим 23 внутренних узла сетки, расположенные на 19 уровнях. Таким образом, число искомых не -известных значений поля dV/dz будет равно

437 (23 19) ,                      437-

,-

,

-«                 +», ( обеспечивает устойчивость решения СЛАУ

),-

920 (23 20 2).-

,-

= 920 874- f = 920 1.

Для формирования элементов матрицы была составлена компьютерная программа prPUAS. ‒ (              , 2004).    -

, 437 ,                           ,                                                   ,,

• 24-                    ,               874-

• ,            4(

23 ). «»

находится во внутреннем узле под номером 1 (     . 3),-

(13)(14)

^1^ИЦ + ^Aj'*’G^M3,1'*’ ^2^2,0 ⁺ (-^2,2 + ^Ц Д1,1 ⁼ О

СМ Р)              (М)(43S)

,

= =1, =-4 ‒-

«               », «»;

;       ‒«-

»                       (-

-

- стид = ft/г/см3 и в условиях двумерной )

( prPDOP);           , ‒-

;‒

(-

-

,

).

Перенесем известные величины в правую (14),-

;

,               (14)(15):

.

• (1)         (2)         (24)(438)

,24

С С г

• 1,    2, 24, 438

(                          43724

‒           )    . .    460.

,

« сой крест». Вектор правой части f = 920x1 в

- pr607KF.-

-

[10];

=920x874           00:00:30 ( -

DELL,                2).

,-

,              874-

,

,

,                                                                 :-

~10 ^-4 -10 ^-3 ,           ~ 10 ^-1 -10 ¹ .

,

• 3                   I, II, III,

  • 181,    18175

• (     . 4),     ,-

• ,,

(          0.1 / 2)-

II , I; III -

,

, (     . 4 , 4 , 4 ).

Для значений поля dV/dz внутри прямого

• (      . 5),

  -

• .-
• ,

• .    5, 5, 5 (          ,            ,-

• );

, . 5 ‒5 ,

- чений поля в небольшом количестве узлов по

,

(9)          ,

.

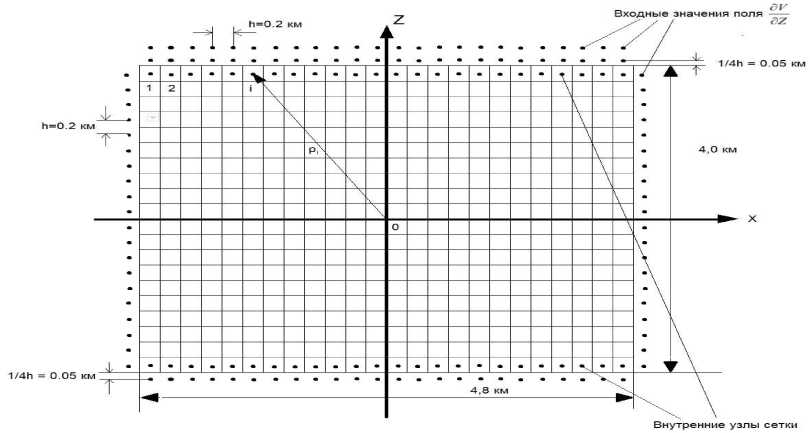
Рис. 3. Расчетная схема модельного примера вертикального пласта

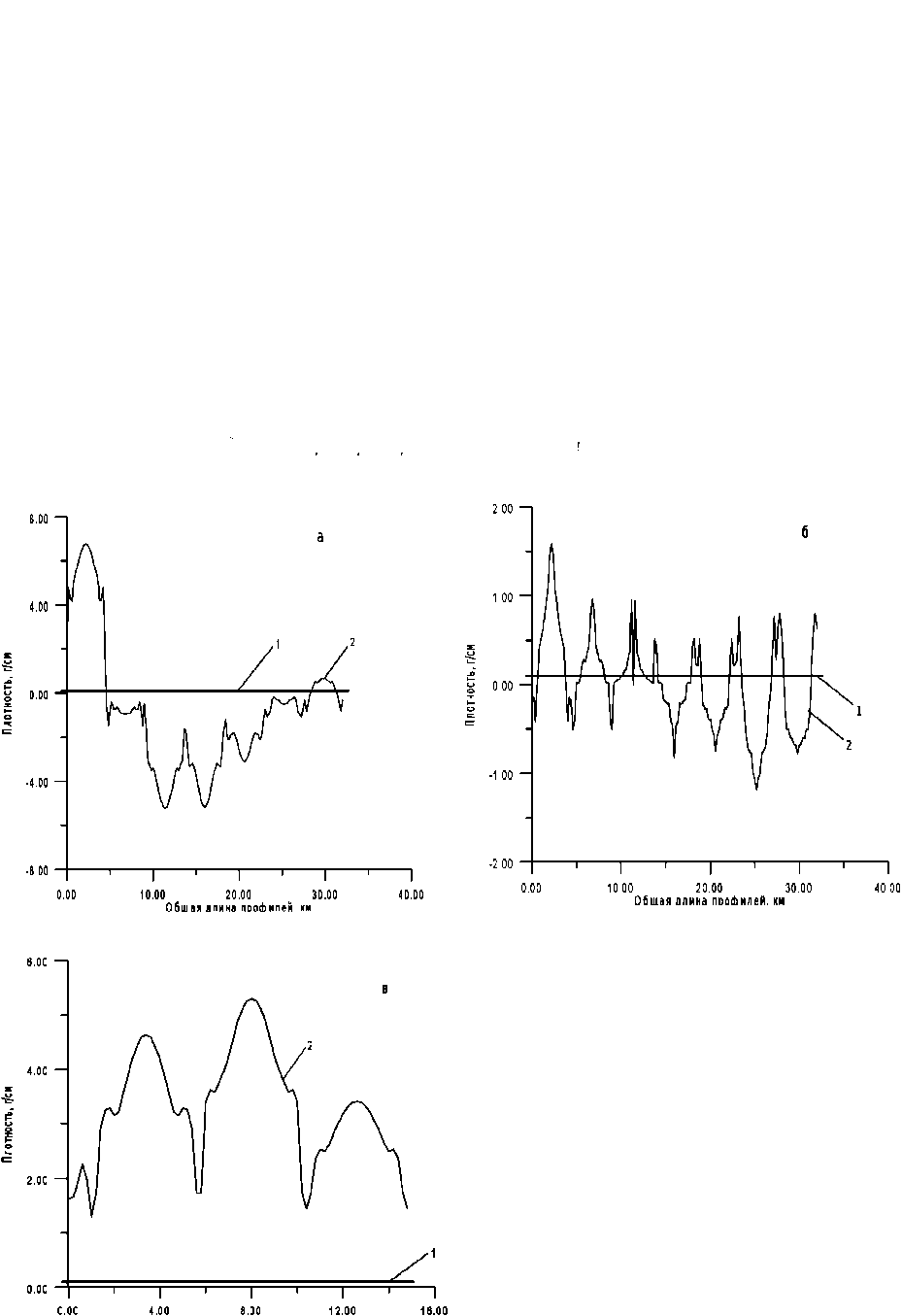
Общая длина профилей, ки

Рис. 4. Результаты расчета плотности тяготеющих

а - область I внутри пласта, содержащая 181 узлов сетки;

б - область II внутри пласта, содержащая 181 узлов сетки; в - область III внутри пласта, содержащая 75 узлов сетки.

• 1-    точное значение плотности, равное 0,1 г/см ;

• 2-    восстановленное значение плотности.

масс

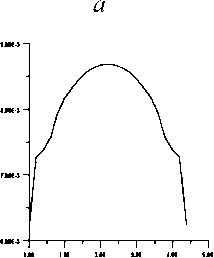
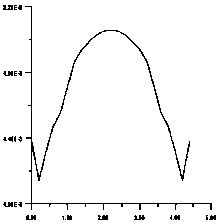
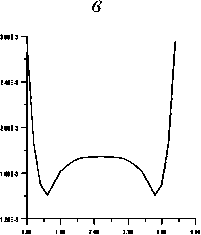
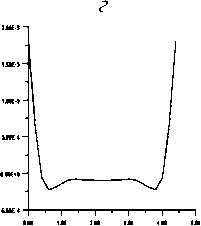
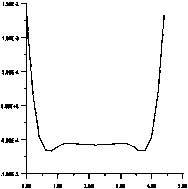
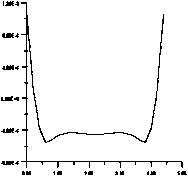
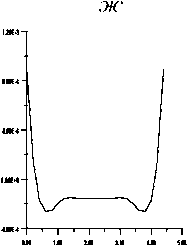
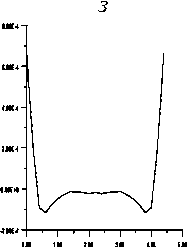
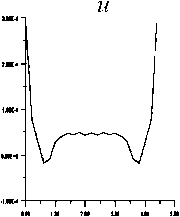
Рис . 5. Результаты расчета поля вертикального градиента гравитационного потенциала . Аномальные кривые поля — ( см /сек² ) внутри вертикального пласта на профилях длиной 4.6 км : ‒ на расстоянии 0.2 км от верхней кромки вертикального пласта ; б ‒ на расстоянии 0.4 км от верхней кромки вертикального пласта ; в ‒ на расстоянии 0.6 км от верхней кромки вертикального пласта ; г ‒ на расстоянии 0.8 км от верхней кромки вертикального пласта ; д ‒ на расстоянии 1.0 км от верхней кромки вертикального пласта ; ‒ на расстоянии 1.2 км от верхней кромки вертикального пласта ; ж ‒ на расстоянии 1.4 км от верхней кромки вертикального пласта ; з ‒ на расстоянии 1.6 км от верхней кромки вертикального пласта ; и ‒ на расстоянии 1.8 км от верх - ней кромки вертикального пласта

Заключение. В результате проведенных исследований установлено, что решение за-дачи аналитического продолжения заданных значений гравитационного поля на поверх-ности Земли позволяет на первом шаге окон-турить область, заполненную тяготеющими массами, а затем на втором шаге ‒ опреде-лить плотность распределения масс в найденной области. Численный расчет, про -веденный на модельном примере с использо-ванием пакета программ, разработанным первым из авторов, показывает, что расчет-ные значения плотности близки к истинным значениям в средней части гравитирующего объекта; а расчетные значения гравитацион-ного поля отвечают в качественном отноше-нии закономерностям в поведении поля внутри масс, предсказанными теорией по-тенциала .