Применение термодинамического подхода к оценке энергетического состояния поверхности дисперсных материалов

оличественной мерой изменения свободной поверхностной энергии для конденсированных сред, другими словами, критерием направленности и самопроизвольности трансформационных процессов (характеристикой запаса свободной поверхностной энергии, которой обладает система) служит величина и знак изменения изобарноизотермического потенциала ∆ G (энергии Гиббса). В частности, изменение свободной поверхностной энергии системы в этом случае определяется характеристической функцией ( ∆ G) и равно:

∆ G = σ •S_уд + S_уд• ∆σ ,                                           (1)

где σ – величина поверхностного натяжения (Н/м); S_уд – удельная площадь поверхности частиц (м²/кг) [1].

Отсюда следует, что величина поверхностного натяжения конденсированной системы является энергетической характеристикой единицы поверхности.

В твердых телах (с размером частиц, как правило, более 10 нм), процесс образования новой поверхности носит необратимый характер. В этом случае классическое понятие поверхностного натяжения как работы обратимого изотермического образования единицы площади поверхности теряет смысл. Кроме того, если в жидкости поверхностное натяжение реализуется в виде стремления сократить поверхность с об-

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

разованием сферических капель, то в твердом теле этому препятствуют механические силы упругости кристаллической решетки. Поэтому, как отмечают авторы [2, 3], параметр σ для твердого тела является мерой накопления энергии в разуплотненном поверхностном слое (мерой свободной поверхностной энергии).

Реальное значение поверхностного натяжения твердого тела определить невозможно, вместе с тем, дать оценку способности вещества уменьшить избыток своей потенциальной энергии на границе раздела фаз можно с помощью критического поверхностного натяжения жидкости ( σ _к) на границе с твердым телом (метод Г.А. Зисмана) [4, 5].

Для использования метода Зисмана на практике необходимо получить зависимость cos θ = f( σ ) для различных жидкостей и, экстраполируя усредненную кривую до cos θ = 1, определить критическое значение поверхностного натяжения σ _к, которое и является характеристикой поверхностной энергии единицы поверхности твердой фазы.

Однако метод Зисмана опробован и показывает хорошие результаты при определении σ _к однородных, беспористых структур, для которых свойственно состояние устойчивого равновесия капли жидкости на границе тех фаз (твердое тело–раствор–воздух), для оценки состояния поверхности дисперсного материала данный метод до настоящего времени не использовался.

Целью данной работы является проверка применимости для дисперсных систем в микро- и наноразмерном состоянии метода Зисмана и расчет на его основе сложной постоянной Гамакера как критерия эффективности контактного межчастичного взаимодействия и структурирования системы.

Для достижения поставленной цели необходимо экспериментально определить значения критического поверхностного натяжения твердой поверхности, образованной частицами разной дисперсности (100 нм … 0,1 мм).

В качестве объекта исследований нами был выбран песчаный грунт, относящийся к типу грунтов «пески пылеватые», предварительно отмытый от глинистых включений и высушенный до постоянной массы при температуре 110оС. Состав полученных образцов был охарактеризован методом рентгенофлуоресцентной спектроскопии на спектрометре Shimadzu EDX-800 HS. Так, 99,8% состава образцов имеют следующее содержание оксидов: SiO2 (58,1%), MgO (8,5%), Al2O3 (9,3%),

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

Fe2O3 (5,1%), CaO (14,7%), K2O (2,4%), TiO2 (0,8%), P2O5 (0,6%), MnO (0,3%). Остальные 0,2% составляют оксиды Ni, Sr, Zn, PbS, Zr, содержание которых в исследуемых образцах песчаного грунта колеблется в пределах 0,1% и ниже.

Из исходного сырьевого материала методом диспергирования были получены четыре фракции с различным размером частиц. Средний размер частиц фракции № 1 определен ситовым анализом и составил 0,10±0,05 мм. Средние размеры частиц фракций № 2, № 3 и № 4 составили 2±1 мкм, 313±89 нм и 102±29 нм, соответственно. Фракция № 2 получена путем измельчения фракции № 1 на шаровой мельнице RetschPM100 (время помола – 30 мин при 420 об/мин). Фракция № 3 получена путем измельчения фракции № 2 на шаровой мельнице RetschPM100 (время помола – 120 мин при 420 об/мин), а фракция № 4 дроблением водной суспензии фракции № 3 на коллоидной мельнице IKAmagicLAB (время помола – 30 мин при 20000 об/мин). Размер частиц фракций №№ 2–4 определялся на установке Delsa Nano Series Zeta Potential and Submicron Particle Size Analyzers. На рис.1 и 2 представлены протоколы измерений размеров частиц для фракций № 3 и 4. В табл. 1 приведено основное (87–92%) распределение по размерам частиц для фракций № 3 и 4.

Для реализации метода Зисмана нами использовались растворы этанола с различным содержанием водной фракции, причем концентрация водной фракции в растворе не превышала 50%. Это связано с ограничениями метода: во-первых, для измерения краевого угла смачивания следует использовать лишь слабополярные жидкости; во-вторых, при величине поверхностного натяжения жидкости более 35 мДж/м2 метод дает высокую погрешность [5].

Характеристика фракций песка № 3 и № 4

Таблица 1

Фракция песка	Распределение по размерам, нм / содержание, %							Средний размер, нм
№ 3	240,5 /21	259,9 /18	280,9/15	303,6/12	328,2/9	354,7/7	383,4/5	313,4 ± 89,9
№ 4	81,1 /25	88,7/20	97,1/16	106,2/12	116,2/9	127,1/6	139,0/4	102,0 ± 29,9

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

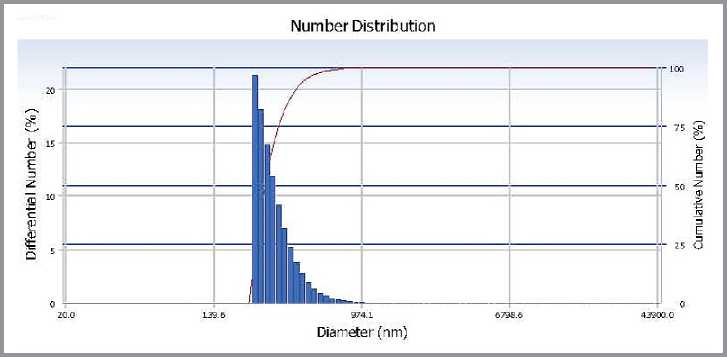
Рис. 1. Протокол испытания образца фракции № 3 по определению размеров частиц на анализаторе DelsaNano

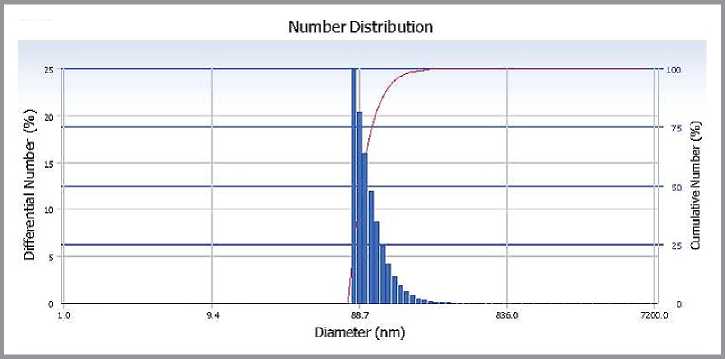
Рис. 2. Протокол испытания образца фракции № 4 по определению размеров частиц на анализаторе DelsaNano

Поверхностное натяжение водных растворов спирта и угол смачивания поверхности дисперсных систем измеряли при температуре 20±1^оС на установке KRUSS Easy Drop. Все эксперименты сопровождались тремя параллельными определениями. В табл. 2 представлены полученные значения поверхностных натяжений используемых водно-спиртовых растворов ( σ _ж).

Для определения угла смачивания материала исследуемых фракций нами были изготовлены образцы путем уплотнения (под давлением 1,5 кПа) дисперсного материала соответствующей фракции в металлической форме диаметром 10 мм.

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

Таблица 2

Значения поверхностного натяжения водно-этанольных растворов

№ п/п	Содержание воды, %	( о ж±0,02)х103, Н/м
1	0	24,74
2	10	26,61
3	20	27,34
4	30	28,11
5	40	28,42
6	50	31,31

При проведении экспериментов по определению краевого угла для образцов различных фракций специализированной компьютерной программой выбиралось время первого контакта жидкости с поверхностью анализируемого образца, которое во всех экспериментах колебалось в интервале 1,0±0,5 сек. Это связано с тем, что за указанный период времени процессами испарения, диффузии жидкости в объемную фазу, капиллярными и другими явлениями, связанными с неоднородностью поверхности (в особенности у образцов фракций № 3 и 4), можно пренебречь. Кроме того, хорошая воспроизводимость результатов измерений может свидетельствовать о существовании в данном временном интервале псевдоравновесного состояния на границе раздела фаз. Протоколы измерений для образца фракции № 3 и 4 приведены на рис. 3, 4.

Для оценки структурообразующих свойств поверхности исследуемых образцов и степени приближения их свойств к поверхностным свойствам однородного материала нами проведены аналогичные исследования с образцом недробленого природного кварца (плотность – 2,65 г/см3)[6].

Полученные экспериментальные данные позволили построить функциональную зависимость cos θ = f( σ _ж) для исследуемых образцов, представленную на рис. 5. В табл. 3 приведены значения коэффициентов линейных уравнений этой зависимости и рассчитанные значения σ _к.

Данные по измерению краевого угла показали, что для всех исследуемых образцов наблюдается линейная зависимость cos θ = f( σ _ж) с удовлетворительным значением коэффициента достоверности аппроксимации R2. Однако для фракций 1 и 2 (размер частиц 0,1 мм и 2 мкм,

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

Рис. 3. Водно-спиртовой раствор на поверхности песчаного грунта (фракция № 3)

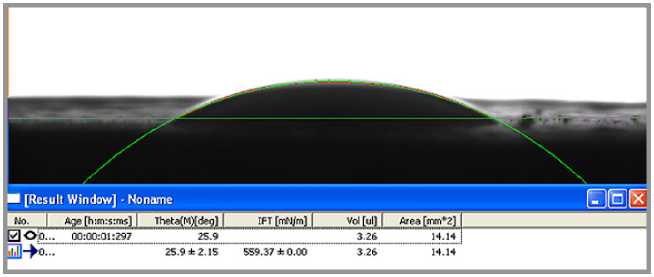
Рис. 4. Водно-спиртовой раствор на поверхности песчаного грунта (фракция № 4)

соответственно) угол наклона линейной функции не соответствует характеристикам твердой поверхности, данный факт может быть свидетельством слабого межчастичного взаимодействия в этих системах, значительной неоднородностью (шероховатостью) поверхности. Вместе с тем, с увеличением степени раздробленности вещества зависимость cos θ = f( σ _ж) приближается к характеристикам, полученным для образца поликристаллического кварца (см. рис. 5, прямая 5).Разброс значений параллельных измерений краевого угла составил ±2^о, что в свою очередь меняет диапазон значений косинуса этого угла (в интервале измеряемых углов 15–40^о) от ±0,002 до ±0,008. Так, например, для средней точки зависимости (30% воды) имеем следующие данные cos θ : 0,905 (кварц); 0,922 (фракция № 3). Для этанола эти значения составили: 0,941 и 0,971, соответственно).

Таблица 3

Значение коэффициентов в уравнении cos6= а стж+b и к

Фракция	Коэффициент		Достоверность аппроксимации, R2	( стк±0,1)•103, Н/м
	а±0,001	b±0,1
Кварц	–0,025	1,6	0,93	24,0
№ 4 (102) нм	–0,027	1,6	0,91	23,7
№ 3 (313) нм	–0,021	1,5	0,96	25,0
№ 2 (2 мкм)	0,260	– 6,4	0,95	28,5
№ 1 (0,10 мм)	0,040	–0,5	0,96	37,5

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

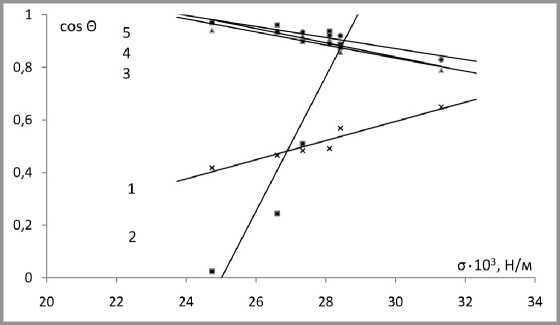
Рис. 5. Функциональная зависимость cosо = f(ст ж ):

1 – фракция № 1 (0,1 мм); 2 – фракция № 2 (2 мкм);

3 – фракция № 3 (313 нм); 4 – фракция № 4 (102нм); 5 – кварц

Б.В. Дерягин с сотрудниками в [7] предлагают метод расчета энергии взаимодействия между частицами, который применительно к нашему случаю сводится к использованию следующего уравнения [8]:

cos θ = 1 +

А*

12nh2 . а

min ж

где h_min – наименьшая толщина пленки, которая соответствует Ван-дер-Ваальсовому расстоянию (0,24 нм); σ _ж – поверхностное натяжение жидкости; A*– сложная постоянная Гамакера, характеризующая взаимодействие жидкости с твердым телом на границе с воздухом, учи-

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

тывающая физическое взаимодействие частиц твердой поверхности. Следовательно, постоянная А* может служить критерием оценки приближения раздробленного состояния вещества к состоянию поверхности твердого тела.

а

б

в

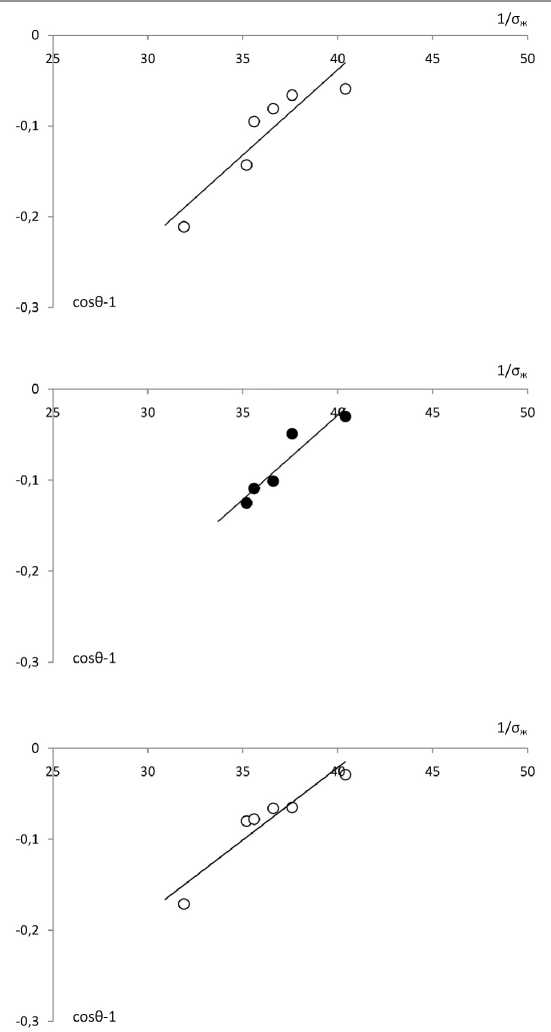
Рис. 6. Функциональная зависимость вида cos0–1= f(1/о_ж): а – кварц; б – фракция 102 нм; в – фракция 313 нм

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

Вместе с тем, следует отметить тот факт, что сложная постоянная Гамакера является аддитивной величиной, состоящей из А11 – постоянной, связанной с взаимодействием частиц дисперсной фазы и дисперсионной среды – А00, а также параметров, связанных с шероховатостью поверхности дисперсного материала, адсорбционными взаимодействиями водно-спиртовой смеси с поверхностью, поэтому можно предположить, что в данном случае А* учитывает в комплексе вышеперечисленные эффекты.

Для расчета сложной постоянной А* нами построены функциональные зависимости cos θ –1 = f(1/ σ _ж) для всех серий эксперимента. На рис. 6 (а, б, в) представлены данные зависимости для фракций с размером частиц 313 нм, 102 нм и кварца. Величина углового коэффициента данных зависимостей (а) связана со сложной постоянной Гамакера следующим выражением:

а =

12лЬ2

min

В табл. 4 приведены значения коэффициентов линейных уравнений данной зависимости. Кроме того, в этой же таблице представлены рассчитанные значения постоянной А*, причем полученные результаты для кварца (А* = 4,1.10–20 Дж) достаточно хорошо совпадают с литературными данными (А101 = 4,5.10–20 Дж), приведенными в [9] для кварцевых нитей на границе кварц-воздух.

Таблица 4

Значение коэффициентов в уравнении cos0–1 = а/о ж +b

Фракция	Коэффициент		Достоверность аппроксимации, R2	(А*±0,1) • 1020, Дж
	а±0,001	b±0,01
Кварц	0,019	– 0,79	0,91	4,1
102 нм	0,018	–0,77	0,93	3,9
313 нм	0,016	– 0,66	0,94	3,4
2 мкм	–0,180	6,17	0,94	–32,8
0,1–0,25 мм	–0,028	0,52	0,95	–18,0

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

Анализируя полученные результаты, необходимо отметить следующее:

• •    метод Зисмана можно применять для определения величины критического поверхностного натяжения нанодисперсного материала и расчета на основе полученных экспериментальных данных сложной постоянной Гамакера;

• •    уменьшение критического значения поверхностного натяжения образцов при увеличении степени дисперсности связано, на наш взгляд, с компенсацией запаса свободной энергии системы за счет усиления межчастичного взаимодействия;

• •    увеличение значений сложной постоянной Гамакера (А*) может свидетельствовать о приближении силы взаимодействия между частицами в нанодисперсном состоянии к характеристикам твердой поверхности;

• •    полученные отрицательные значения постоянной А* для фракций 1 и 2, ограничивают применимость рассматриваемого подхода к грубодисперсным системам,что объясняется значительной неоднородностью поверхности образцов и слабым межчастичным взаимодействием.

Работа выполнена при поддержке Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.

М.А. ФРОЛОВА и др. Применение термодинамического подхода к оценке энергетического состояния поверхности...

Уважаемые коллеги!

При использовании материала данной статьи просим делать библиографическую ссылку на неё:

Фролова М. А., Тутыгин А. С., Айзенштадт А. М. Применение термодинамического подхода к оценке энергетического состояния поверхности дисперсных материалов // Нанотехнологии в строительстве: научный Интернет-журнал. М.: ЦНТ «НаноСтроительство». 2011, Том 3, № 6. C. 13–25. URL: (дата обращения: __ ____________).

Dear colleagues!

The reference to this paper has the following citation format:

Frolova M.А.,Tutygin A.S., Ayzenstadt A.М. Application of the thermodynamic approach to the assessment of the surface energy state of the disperse materials. Nanotechnologies in Construction: A Scientific Internet-Journal, Moscow, CNT «NanoStroitelstvo». 2011, Vol. 3, no. 6, pp. 13–25. Available at: (Accessed _________ ____). (In Russian).