Применение вариационного метода Канторовича на примере решения двумерного нестационарного волнового уравнения
Автор: Коробейников А.Г.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Технические науки
Статья в выпуске: 1-1 (52), 2021 года.
Бесплатный доступ
В работе, на примере решения двумерного нестационарного волнового уравнения, приведено описание применения процедуры прямой минимизации функционала при помощи приведения к системе обыкновенных дифференциальных уравнений. Данная процедура называется методом Канторовича. Рассмотренное волновое уравнение применяется в различных предметных областях, например, в теории упругости. Поэтому нахождение его решения представляет практический интерес. В работе проведен анализ динамики упругой мембраны при внешней гармонической сосредоточенной нагрузке. Точное определение величины прогиба прямоугольной мембраны-элемента в месте воздействия гармонической сосредоточенной нагрузки при нестационарных колебаниях, является крайне важной задачей при проектировании упругих чувствительных элементов современных микромеханических преобразователей. В предлагаемом исходном коде на языке Maple содержится множество комментариев, которые помогут понять, как можно модифицируется заданная математическая модель объекта. Кроме того, решение можно вывести в графическом виде, что позволяет достаточно легко проводить анализ на предмет его зависимости от координатных функций и их количества.
Математическая модель, обыкновенное дифференциальное неоднородное уравнение, волновое уравнение, δ-функция дирака, прямая задача, гармоническое воздействие, нестационарное воздействие, сосредоточенная нагрузка, вариационные методы, минимизация функционала, метод канторовича
Короткий адрес: https://sciup.org/170190875
IDR: 170190875 | DOI: 10.24411/2500-1000-2021-1044
Текст научной статьи Применение вариационного метода Канторовича на примере решения двумерного нестационарного волнового уравнения
В настоящее время, начиная работу по созданию сложных технических систем, необходимо знать путь их наилучшего проектирования. Современный подход для решения таких задач подразумевает привлечение математического и компьютерного моделирования, а вариационные методы являются эффективным инструментарием при анализе различных математических моделей (ММ) [1]. В качестве программного инструментария, применяемого при компьютерном моделировании, используют такие системы как MATLAB, Maple и др [2-5]. С их помощью решают задачи в различных предметных областях [5-10].
В работе, базируясь на теории Кирхго-фа-Лява, в качестве ММ было выбрано нестационарное двумерное волновое уравне-
ние, описывающее динамику упругой мембраны-полосы при воздействии внешней гармонической сосредоточенной нагрузкой по заданной линии [11]. При таком воздействии возникают деформационные изменения на линии нагружения мембраны. Нагрузка на линию задана с помощью дельта-функции Дирака. Величина прогиба мембраны-элемента является решением заданной ММ.
Постановка задачи
Задача математического моделирования динамики упругой мембраны-полосы с закрепленными краями при воздействии на нее внешней гармонической сосредоточенной нагрузкой по заданной линии ставилась и решалась при помощи различных методов [12]. ММ данного процесса может служить следующее нестационарное волновое уравнение [11]:
д2 u (x, y, t) _ 2
дt2 cC
д2 u (x, y, t) д2 u (x, y, t )л
дx2
д y y
+ F (x, y, t)
где: u ( x , y , t ) - перемещение точек в упругой мембране - полосе;
F ( x , y , t ) - внешнее воздействие (сила).
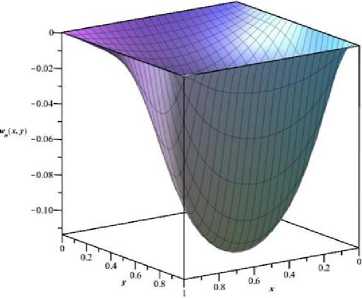
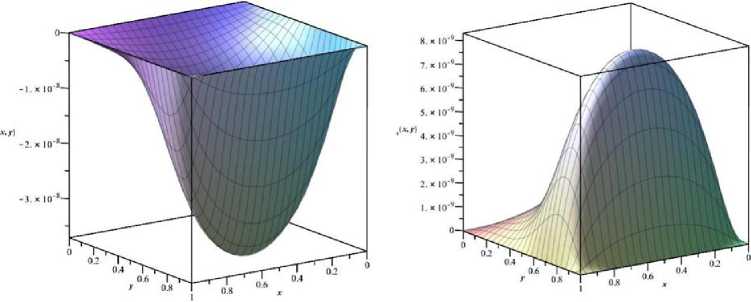
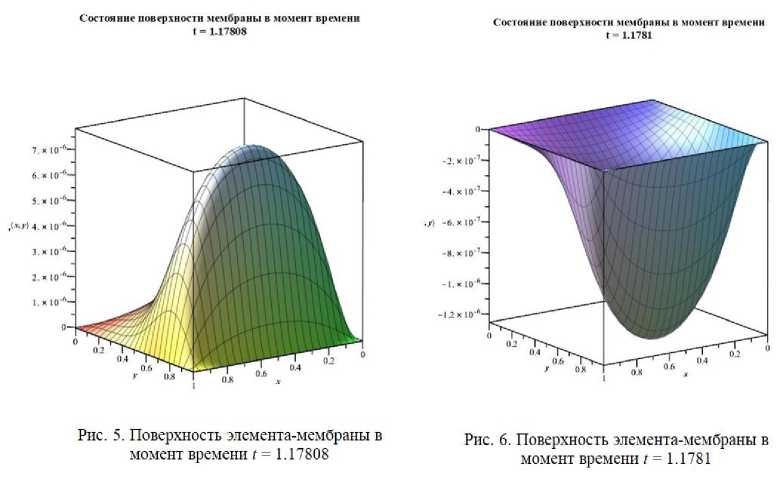
Так как рассматривается мембрана-полоса, то решение (1) будем искать в области D = {(x,y,t) |0 t - время. Зададим внешнюю гармоническую сосредоточенную нагрузку по оси Oy следующим образом: F ( x, y, t ) = F„ cos( rot)-5 ( y - y о). (2) где: 5(□) - дельта функция Дирака; го - заданная частота воздействия; Fo- заданная амплитуда воздействия. Так как края мембраны-полосы жестко закреплены, то граничные условия имеют следующий вид: u (x, y, t )L=u (x, y,t )L =u (x, y,t )L=u (x, y, t )L = 0 I x — О lx — lx Iy — О yz — ly Таким образом, задача состоит в моделировании состояния (1) с учетом (2) и (3) в области D . Поиск решения Решение (1) будем искать в следующем классе функций: u ( x, y, t) — cos(rot) - w ( x, y ). Такой выбор продиктован условием задания гармонического внешнего воздействия -поэтому и отклик должен быть гармонической функцией. Подставив (4) и (2) в (1), получим следующее уравнение: д2 cos (rot) w(x, y) 2д/2 — c д2 cos (rot) w(x, y) д2 cos (rot) w(x, дx x ^ -ro2 ■ cos (rot)■ w(x, y) — c2 ■ cos (rot) ^ -ro2 ■ w ( x, y ) — c2 ■ 5y2 д2 w (x, y) д2 w (x, +Focos(rot) ■5 (y - y о) дx2 дy y ^д2 w (x, y) д2 w (x, y )^ дx2 + F0cos(rot) ■5 (y - y о) + F0 ■5 (y - y 0) c ^ w(X, y ) + — • to д2w ( x, y ) д2w ( x, дx2 дy2 z) 1+to. §(y -y0) — 0 Решение (5) будем искать при помощи методов теории вариационного исчисления. Для этого, сначала, необходимо решить обратную задачу вариационного исчисления - найти функционал, для которого уравнение (5) является уравнением Эйлера - Лагранжа. В данном случае искомый функционал имеет следующий вид: lx ly J [ w (x, y )] — jj Udydx, 0 0 где Лагранжиан U равен: c U — w2 (x, y)--- to • ffw^ ^ I ox V 2 г^ ^ l дy J J F + 2• § (y-y о )• — •w (x, y). (7) to Приведем доказательство этого факта, или, что эквивалентно, найдем функцию Эйлера – Лагранжа. Для удобства введем следующие w — w ( x, y ); wx _ д w (x, y) _ дx ; wy _ dw (x, y) _ дy д2w ( x, y ) wxy— —; wxx дx дy обозначения: _ д2w (x, y), дx2 w yy _ д2w (x, y) дy2 • В этих обозначениях уравнение (7) будет иметь следующий вид: U = w2 c2 , . F --2 •( wx + wy ) + 2• § ( y- y о )• -^ • w. to x ' to Кроме того: : Uw U — 2w + 2• §(y-yо)• -^; U, д w to x д д wx U — -2 • c • wx; to U —— wy 'w U —-2 • cL • wy • to Функция w, доставляющая экстремум функционалу (6), должна удовлетворять уравнению Остроградского [1]: U - — U - — U — 0, w w, w., , дx x дy y где °- Uw дx x — U дy wy — U + U • w + U wxx wxw x wxwx • w + U xx w w xy — U + U • w + U wyy wyw y wywy • w ; xy • w + U yy wx wy • wxy • Подставив в (8) полученные выше выражения, имеем: F 2w + 2 • S (y-y о )“-to - ( ^ —2 • w xx V to 7 - V . c2 -2• wyy to \ = 0 cF ^ w + — ( wxx + wyy ) + "1 • 6 ( y - y0 ) = 0. to x ' to Это уравнение с точностью до обозначений совпадает с (5). Таким образом показано, что (6) является требуемым функционалом. Таким образом, задача нахождения решения (5) перешла в задачу нахождения экстремали w(x, y), на которой функционал (6) достигает минимума. В данной работе эта задача решается при помощи метода Канторовича (называемого также иногда процедурой Канторовича), переводящей задачу для уравнения в частных производных в систему Эйлера-Лагранжа в виде обыкновенных дифференциальных уравнений [1]. При помощи этой процедуры строится приближенное решение с привлечением координатных функций {фк (x,У)} : Коэффициенты строят так, чтобы новый функционал: m wm ( x, У ) = Z “k ( x ) Фк ( x, У ) . к=1 ак (x) в (9) являются неизвестными функциями от x. Сумму в (9) wm (x, y) удовлетворяла условиям (3). Подставляя (9) в (6), получим lx ly J [ wm (x, У )] = J J Udydx о 0 Зависимость лагранжиана U от переменной y задана выражением (9), и поэтому считается известной. Проинтегрировав (10) по y, получим функционал, зависящих от т неизвестных функций а1 (x), а2 (x) ,ее.,ат (x): lx Ф[«1 (x) , • ••, am ( x )] = J V ( x’ “1 ( x ) ’ • ее ,«m ( x ) »«1 ( x ) , еее ,«m (x)) dx. Для достижения минимума функционала (11) следует так выбрать а1 (x),а2 (x),.ее,ат (x),чтобы они удовлетворяли системе уравнений Эйлера - Лагранжа: Va - — V' = 0 a1 dx Va - — V. = 0 “2 dx Va -d-У.= I am dx и граничным условиям, заданных на x = 0 и x = lx . Подставив найденные решения ak (X) в (9), получим решение приближенное wm ( x, y) для (5), а затем и решение для (4). Результаты моделирования Рассмотренная процедура была реализована в Maple под управлением операционной системы Windows 10 с подключение CUDA [2-4,14]. Исходный текст для поиска решения (1) может выглядеть следующим образом: > > > > т > ' i = 1 > ту Lagrang — ^х,у^--7- — (с/(х,у)) + ——(и(х,у)) +и(х,у) + 2 —^'«ку) : со' > > # Исходные данные 1 := 1 : / — 1 : > > > > > > > > > > > > > со ;= 4 : с := 2 : Уо := 0.75 : m — 4 : ТТ — cp(x,_v, /„) : #Подключение CUDA #CUDA:-IsEnabled( ) : CUDA'.-Enable^true) : CUDA'.-IsEnabled( ) : #3адаем время time_0 — time( ) : #3адаем f #Подставляем аппроксимацию и функцию/ > ту-Functional_ху — ■ТТ1 + 2-Дх,уУТТ\ : > > > > > > / ту_Ф — I my_Functional_xy dy : my_eq — EulerLagrange^myjF,x, [лес/^ а^х\1= 1 "w)]) : my ODE sys — seq^ my_eqf z = 1 ..m^ : my Init Condision_1 — seq^ a^Q) = 0, i = 1 ,.m) : my_Init_Condision_2 — seq^ a^x)= 0, z = 1 ,.m^ : my_solv_IC := evalf ydsolvei [my_ODE_sys, my_Init_Condision_l, my_Init_Condision_2^ ) : > #Время выполнения > time-Выполнения — time) ) — time_O: > CUDA:-Enable(false) : > CUDA:-IsEnabled{) : > > > > TTmysolvIC — evalj'^subs^seq^a^x^ = rhs)my_solv_IC\i]),i = 1 ..my TT^ : TT_my_solv_IC — subs{I= 0, TT_my_solv_lC) : my_s — "Решение w(x,y)" : plot3d)TT_my_soh’_IC, x = 0 Jx, у = 0.7^, labels = | 'x',y,'w;7 (x,y)'], labelfont = [ TIMES, BOLD, 10], title■ = my_s, titlefont = [TIMES, BOLD, 15]) >my_s — "Состояние поверхности мембраны в момент времени\п1 = " : >t — 0 : TT_my_solv_IC_t — cos(to-c) -TT_my_solv_IC: sO — cat[my_s, convertf, string)) : > > plot3dyTT_my_solv_IC_t,x = 0 Jx,y = 0.7^, labels = ['x',y,'w7(x,y)'], labelfont = [TIMES, BOLD, 10], title = sO, titlefont = [ TIMES, BOLD, 15]) t — 0.392699 : TT_my_solv_IC_t — cos(cov) -TT_my_solv_IC: sO — cat[my_s, convert)!, string)) : > > plot3dyTT_my_solv_IC_t,x = 0 Jx,y = 0 ..1у, labels = )'x',y,'w7(x,y)'], labelfont = [TIMES, BOLD, 10], title = sO, titlefont = [ TIMES, BOLD, 15]) t — 0.3926991 : TT_my_solv_IC_t — cos( to v) • TTjnysolvIC: sO — cat)my_s, convertf, string)) : > > ploi3d[TT_my_solvJC_i,x = 0 ..i^y = 0 ,.1у, labels = )'х',У','и;;7(х,у)'], labelfont = [TIMES, BOLD, 10], title = sO, titlefont = [ TIMES, BOLD, 15]) t — 1.17809: TT my solv ICj — cos^to-ty TT my solvIC: sO — cat[my_s, convertf, string)) : > > plot3dyTT_my_solv_IC_t,x = 0 ..lx,y = 0.7^, labels = )'х',]у','^(х,у)'], labelfont = [TIMES, BOLD, 10], title = sO, titlefont = [ TIMES, BOLD, 15]) t — 1.1781 : TTmysolv IC_t — cos( O) v)-TTmysolvIC: sO — cat(my_s, convertf, string)) : > plot3dyTT_my_solv_IC_t,x = 0 ,.lx,y = 0.7^, labels = )'х',У','и’;7(х,у)'], labelfont = [TIMES, BOLD, 10], title = sO, titlefont = [ TIMES, BOLD, 15]) На рисунке 1 представлен график полученного решения уравнения (5). На нем хорошо виден результат постоянного воздействия на мембрану-элемент по линии у0 = 0.75 . На рисунках 2-6 представлены состояния мембраны-элемента в заданное время. Как видно, рис. 1 и 2 совпадают, как и следовало ожидать. На рис. 3, 4 показан переход из нижнего полупространства в верхнее. На рис. 5, 6 показан переход из верхнего полупространства в нижнее. Решение w(x,v) Состояние поверхности мембраны в момент времени t = 0 Рис.1. График решения уравнения (5) Рис. 2. Поверхность элемента-мембраны в момент времени г= 0. Состояние поверхности мембраны в момент времени t= 392699 Состояние поверхности мембраны в момент времени t = 3926991 Рис. 3. Поверхность элемента-мембраны в момент времени г = 0.392699 Рис. 4. Поверхность элемента-мембраны в момент времени / = 0.3926991 Заключение. В статье предложен подход, который можно применять для численного решения дифференциальных уравнений в частных производных второго порядка, относящиеся к гиперболическому типу. Представленный исходный код легко модифицируем, то есть при помощи замены функционала можно решать достаточно много задач, относящихся к задачам математической физики. Кроме того, можно мощи оператора time(), которое существенным образом зависит от выбора коли . к (x, y)} чества координатных функций k . Необходимо отметить, что при помощи процедуры Канторовича получают достаточно точные решения [1]. Поэтому на практике достаточно часто можно ограничиться выбором небольшого числа координатных функций. контролировать время решения, при по-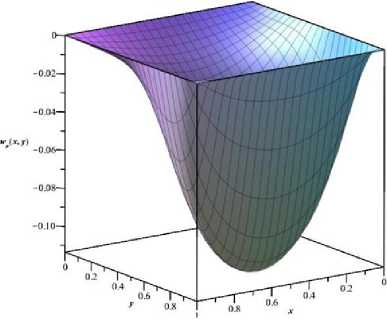
Список литературы Применение вариационного метода Канторовича на примере решения двумерного нестационарного волнового уравнения
- Глазунов Ю.Т. Вариационные методы. - Москва-Ижевск: НИЦ "Регулярная и хаотическая динамика"; Институт компьютерных исследований, 2006. - 470 с.
- Коробейников А.Г. Проектирование и исследование математических моделей в средах MATLAB и Maple. - СПб: СПбГУ ИТМО, 2012. - 160 с.
- Коробейников А.Г., Гришенцев А.Ю. Разработка и исследование многомерных математических моделей с использованием систем компьютерной алгебры. - СПб: НИУ ИТМО, 2014. - 100 с.
- Коробейников А.Г., Ахапкина И.Б., Безрук Н.В., Демина Е.А., Ямщикова Н.В. Применение системы компьютерной алгебры Maple в обучении проектированию и анализу многомерных математических моделей // Информатика и образование. - 2014. -№ 253. - С. 69.
- Гришенцев А.Ю., Гурьянов А. В., Кузнецова О. В., Шукалов А.В., Коробейников А.Г. Математическое обеспечение в системах автоматизированного проектирования. - СПб: Университет ИТМО, 2017. - 88 с.


