Применение вейвлет-преобразований для анализа рассеяния сверхширокополосных сигналов объектами сложной формы

Анализ рассеяния сверхширокополосных (СШП) Согласно [1], распределение отраженного сиг- сигналов объектами сложной формы имеет значение для разработки средств снижения контрастности радиолокационных целей и совершенствования способов передачи информации по локальным сетям радиосвязи и управления в условиях сложного рельефа местности и городской застройки [1].

Вторичное излучение объекта, в основном, формируется полями, рассеянными отдельными участками его поверхности с доминирующими отражательными свойствами. По мере увеличения эквивалентной ширины спектра сигнала возрастает эффективность разрешения локальных рассеивателей по времени запаздывания откликов, зависящего от ракурса облучения [1; 2]. За счет различения интенсивности вторичного излучения отдельных элементов обеспечивается стабилизация положений энергетических центров объектов [3].

В предлагаемой работе на основе измерений мгновенных амплитуд, выполненных стробоскопическим методом на дискретных интервалах времени [2], и вейвлет-преобразований [4] отраженных сигналов исследованы интегральная эффективная поверхность рассеяния (ЭПР) и локальные ЭПР объекта сложной формы.

Цель работы – анализ частотных зависимостей интегральной и локальных ЭПР объекта и определение параметров вейвлет-преобразова-ний для выявления доминирующих центров вторичного излучения СШП сигнала.

нала во временной области u ( t ) находится путем последовательной свертки облучающего сигнала e ( t ) с импульсными характеристиками среды распространения и объекта [1; 2].

Интегральная ЭПР объекта на текущей частоте в спектре сигнала f определяется выражением [5]

о ( f ) = 4 п RGf , (1) G 2 ( f )

где G 2 ( f ) и G ² ( f ) — энергетические спектры облучающего и отраженного сигналов; R – расстояние до точки регистрации отраженного сигнала в дальней зоне объекта, граница которой определяется как отношение удвоенного значения квадрата его характерного размера к эквивалентной пространственной длительности сигнала [5].

Локальные ЭПР объекта ст L ( f ) , j = 1, 2, ..., определяются с использованием (1) при замене G ² ( f ) энергетическими спектрами G Lj ( f ) откликов локальных центров вторичного излучения [6; 7].

Внешний вид исследуемого объекта сложной формы, состоящего из элементарных отражателей с высоким уровнем вторичного излучения в различных секторах углов [8], представлен на рис. 1.

При измерениях ЭПР объект облучался коротким СШП импульсом, зависимость которого

Рис. 1. Объект сложной формы

от времени приведена на рис. 2 под номером 1; отраженные сигналы подвергались когерентному накоплению, их энергетические спектры вычислялись на основе быстрого преобразования Фурье.

В [6] показано, что используемый сигнал в точке облучения объекта на множестве N дискретных отсчетов по времени e ( t ) ® e ( k ) , k = 0, .., N - 1, может быть аппроксимирован реальной частью комплексного вейвлета Морле [4]

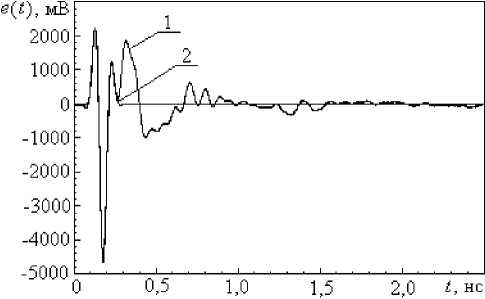
Рис. 2. Сигнал в точке облучения (зависимость 1) и реальная часть аппроксимирующего комплексного вейвлета Морле (зависимость 2)

– диапазон изменения параметра масштаба вейвлета а = 1 ^ 400;

– диапазон изменения параметра сдвига вейвлета b = 0 ^ N - 1;

– расстояние между центрами вторичного излучения L b = 15 A t k b k ;

morlet ( k ) = exp

k

-

+ iwk

z

с параметрами w = 3,7 и z = 0, 8, выбранными из условия минимизации невязки спектров в максимально широкой полосе рабочих частот.

С учетом параметров масштаба « a » и сдвига « b » [4] базисная вейвлет-функция может быть представлена в виде

– время регистрации отраженных от них сигналов t k = A t k b k .

Локальный энергетический спектр G ² _Lj ( f , b_{j max} ) для фиксированного значения b_{j max} , соответствующему моменту времени t_{k max} или дальности L_{bj max} , j -го центра вторичного излучения, j = 1, 2, ..., определяется из (5) путем замены переменной масштаба « a » на текущее значение частоты f

Т ( a , b , k ) = a 12 morlet

b - k

a

f = a - 1

a j max f 0 j max ,

Для нахождения локальных энергетических частотных спектров центров рассеяния выполняется прямое вейвлет-преобразование отраженного сигнала в приближении u ( t ) ® u ( k ) , k = 0, ..., N - 1,

N - 1

с ( a , b ) = ^ u ( k ) Т ( a , b , k ) .                     (4)

k = 0

Семейство вейвлет-спектров коэффициентов с ( a , b ) представляется в виде двумерного массива

G ² ( a , b ) = | с ( a , b ) 2 ,                                   (5)

содержащего информацию об изменении относительного вклада вейвлет-коэффициентов различного масштаба « a » в зависимости от параметра сдвига « b ».

Обработка сигнала u ( t ) осуществлялась при следующих условиях:

— время дискретизации сигнала A t k = 0,001221 нс;

где a_{j max} – значение параметра масштаба « a » для максимального значения энергетического вейвлет-спектра j -го центра, соответствующего значению b_{j max} ; f _{0 j max} – частота отраженного сигнала, соответствующая максимальному

значению локального энергетического спектра G Lj ( f , b j max ) . Значение f j ma _X находится с использованием коррелирующей вейвлет-функции (3) при a_{j max} , b_{j max} и является его центральной вейвлет-частотой. Из (6) следует, что выражение

для определения локального энергетического частотного спектра GL j (f) при произвольной величине b , j = 1, 2, . , имеет вид j max

G L j ( f ) = | с ( f , b j )².                                       (7)

На рис. 3 представлены зависимости энергетических вейвлет-спектров G Li ( L b ) от дальности L_b при различных значениях параметра масштаба « a ».

Из них следует, что с повышением частоты облучающего сигнала изображение объекта приобретает более детальный характер. На ча-

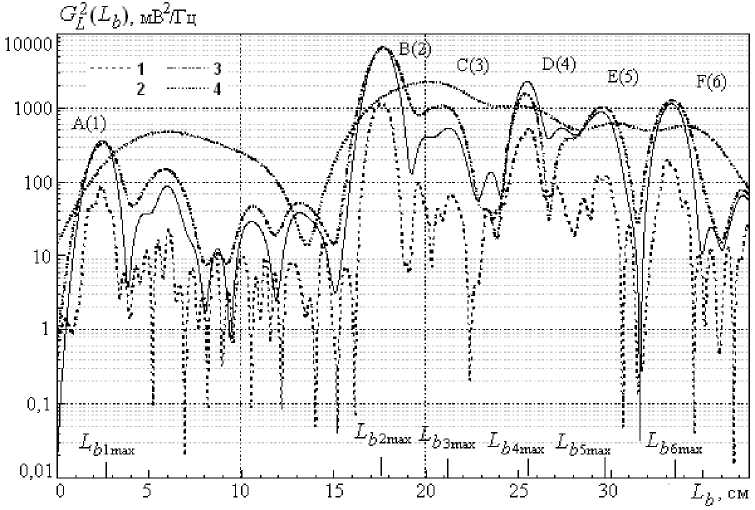
Рис. 3. Зависимости энергетических вейвлет-спектров G_L j ² ( L_b ) отраженного сигнала от дальности L b при различных значениях параметра масштаба (1 — а = 20 (частота f = 17,868 ГГц); 2 — а = 60 (частота j 2 = 7,445 ГГц); 3 — а = 80 (частота f = 5,584 ГГц); 4 — а = 200 (частота jj = 2,233 ГГц))

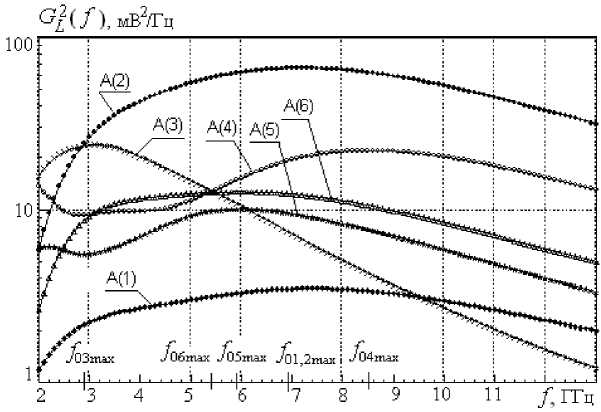
Рис. 4. Зависимости локальных энергетических спектров G 2^ ( L b ) центров вторичного излучения объекта от текущего значения частоты сигнала

Таблица

Параметры центров вторичного излучения объекта

Наименование параметра	Значение параметра
L bj max , см	2,6	17,6	21,1	25,5	29,7	33,4
t kj max , нс	0,171	1,172	1,404	1,697	1,978	2,222
a j max	65	65	260	55	78	90
f 0 j max , ГГц	6,872	6,872	1,718	8,122	5,727	4,963
j max	140	960	1150	1390	1620	1820

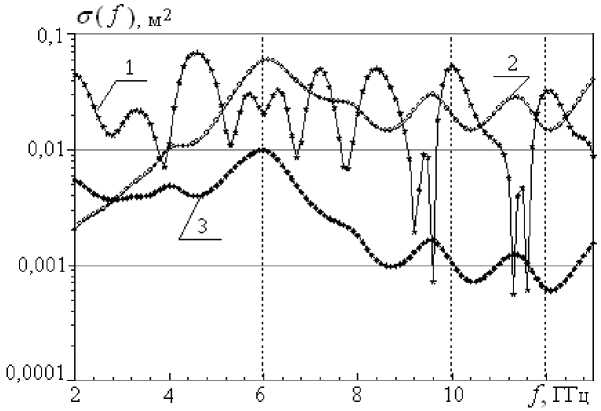
Рис. 5. Частотные зависимости ЭПР объекта сложной геометрической формы (1 — интегральная ЭПР; 2 и 3 — локальные ЭПР доминирующих центров вторичного излучения B(2) и C (3))

стоте f 4 = 2,233 ГГц проявляется только контур объекта, на частоте f = 17,868 ГГц различимы даже мелкие отражающие центры. Уровень отраженного сигнала достигает наибольших значений в окрестностях частот f 2 = 7,445 ГГц и / з = 5,584 ГГц, где проявляются наиболее интенсивные центры отражений.

В таблице приведены найденные на основе указанных зависимостей и (3)–(5) параметры вейвлет-преобразования a_{j max} , b_{j max} , временные координаты t_{kj max} , координаты дальности L_{b j max} и центральные частоты коррелирующих вейвлетов f _{0 j max} центров наиболее интенсивного вторичного излучения сигналов A(1), B(2), C(3), D(4), E(5), F(6).

На рис. 4 представлены зависимости локальных энергетических спектров G L j ( f , b j max ) для локальных центров вторичного излучения A(1), B(2), C(3), D(4), E(5), F(6) исследуемого объекта в полосе частот 2...13 ГГц.

На рис. 5 приведены вычисленные с использованием (2) интегральная и локальные ЭПР центров наиболее интенсивного отражения сигнала B(2) и C(3) исследуемым объектом.

Представляя отраженный СШП сигнал последовательностью отсчетов в моменты времени t_j , j = 1, 2, . . , находим, что каждый из них соответствует j -му поперечному сечению объекта, j = 1, 2, ..., расположенному на дальности L bj , j = 1, 2, . Эти сечения представляют собой набор частотных фильтров; наиболее прозрачные из них, пропускающие отраженный сигнал с малыми потерями, могут идентифицироваться как доминирующие локальные центры вторичного излучения.

Таким образом, на основе измерения мгновенных амплитуд, выполненного стробоскопическим методом на дискретных интервалах времени, и вейвлет-преобразований отраженных сигналов исследованы интегральная и локальные ЭПР объекта сложной формы, облучаемого СШП импульсом.