Применение вейвлет-преобразования и метода Прони для идентификации биогенных сигналов

Введение. Технологии цифровой обработки сигналов и их изображений находят все более широкое применение в различных областях, в частности при определении характеристик и идентификации биогенных сигналов.

Разработка алгоритма для анализа биогенного сигнала, однако, является непростой задачей; довольно часто это даже не целенаправленный процесс. Инженер или компьютерный аналитик часто бывает поражен изменчивостью и разнообразием признаков в биогенных сигналах и системах, где эти факторы проявляются в большей степени, чем в физических системах или наблюдениях. Учет всех возможностей и степеней свободы в биогенных системах является наиболее сложной проблемой для большинства применений. Методы, показавшие свою пригодность для работы с определенными системами или наборами сигналов, могут оказаться несостоятельными в других, на первый взгляд похожих, ситуациях.

Так, для получения правдивого результата биогенного сигнала следует иметь расслабленное и спокойное состояние при отсутствии движений. Кашель, напряжение мышц, движения глаз, конечностей вызывают соответствующие сигналы, играющие роль нежелательных артефактов. В результате рекомендацией при снятии сигнала служит задержка дыхания на несколько секунд. Но это предложение неприемлемо для пациентов в критическом состоянии или при проведении диагностики у младенцев.

В таких и других случаях для удаления артефактов используются методы цифровой обработки сигналов.

Обработка сигналов, связанная с анализом их спектров, называется спектральным анализом. Спектральный анализ используется при распознавании, обнаружении и сжатии сигналов. В основе спектрального анализа сигналов лежит интегральное преобразование и ряды Фурье.

Идентификация особенностей биогенных сигналов – весьма важный этап, так как допущенные ошибки сказываются на правильности врачебного заключения [1].

Постановка задачи. Исследовать методы идентификации для устранения артефактов, способных искажать биогенные сигналы, без ухудшения качества исследуемых сигналов. Применить хорошо разработанные методы Фурье с помощью дискретного преобразования Фурье (ДПФ), используя алгоритм быстрого преобразования Фурье (БПФ). Применить вейвлет-преобразование и метод Прони для анализа и параметризации нестационарных сигналов. Провести оценку погрешности и сравнительный анализ полученных результатов.

Методы обработки нестационарных сигналов. Большинство биогенных сигналов имеет сложные частотно-временные характеристики. На рис.1 представлен нестационарный кардиосигнал биогенного характера, на примере которого рассматривается идентификация сигналов. Как правило, такие сигналы состоят из близких по времени, короткоживущих высокочастотных и долговременных, близких по частоте низкочастотных компонент.

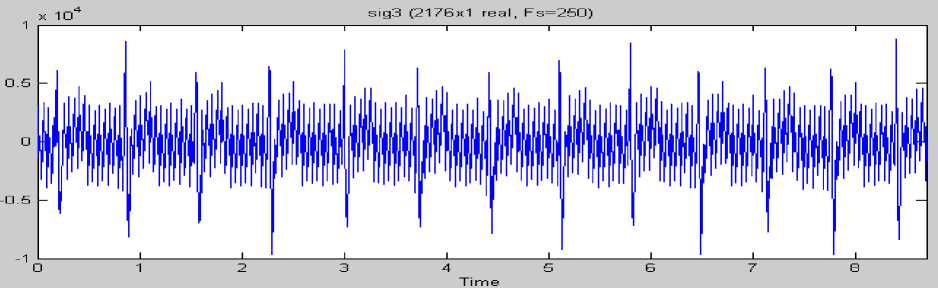
Рис.1. Кардиосигнал (ЭКГ), содержащий шумы

Для анализа таких сигналов нужен метод, способный обеспечить хорошее разрешение и по частоте, и по времени. Первое условие требуется для локализации низкочастотных составляющих, второе – для разрешения компонент высокой частоты.

Преобразование Фурье – сигнал, заданный во временной области, в виде разложения по ортогональным базисным функциям (синусам и косинусам), при этом выделяются частотные компоненты [2]. Недостаток преобразования Фурье заключается в том, что частотные компоненты не могут быть локализованы во времени, что накладывает ограничения на применимость данного метода к ряду задач (например, в случае изучения динамики изменения частотных параметров сигнала на временном интервале).

Вейвлеты представляют собой семейства математических функций определенной формы, которые локальны во времени и по частоте, и в которых все функции получаются из одной базовой (порождающей) посредством ее сдвигов и растяжений по оси времени. Вейвлетные функции базиса позволяют сконцентрировать внимание на тех или иных локальных особенностях анализируемых процессов, которые не могут быть выявлены с помощью традиционных преобразований Фурье.

Метод Прони – это метод анализа коротких отрезков сигнала, основанный на аппроксимации сигнала конечной суммой комплексных экспонент (рис. 2–3), т.е. на подгонке экспоненциальной модели к измеренным эквидистантным (равноотстоящим, равноудаленным) значениям и последующем вычислении дополнительных значений посредством оценки параметров этой экспоненциальной модели в промежуточных точках.

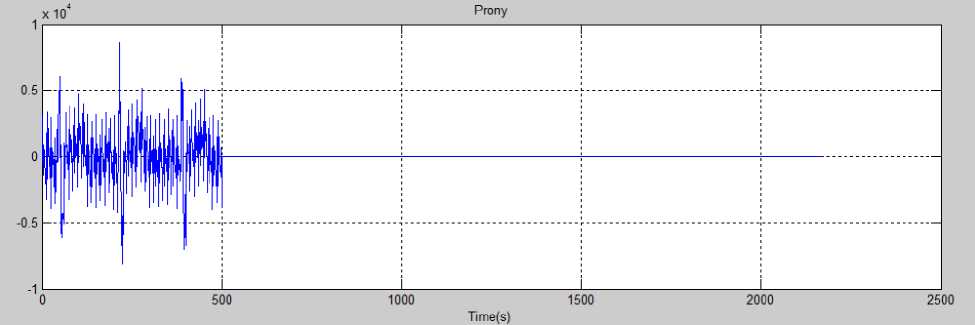
Рис. 2. Короткий отрезок кардиосигнала, обработанный методом Прони (сумма комплексных экспонент)

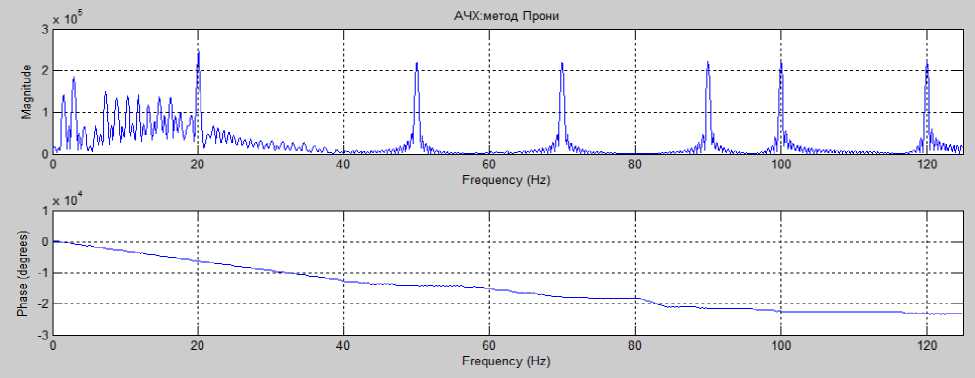
Рис. 3. Спектр короткого отрезка сигнала и фаза после анализа методом Прони

Краткий обзор преобразования Фурье. Классическим методом частотного анализа сигналов является прямое преобразование Фурье:

∞

S' ( to ) = j 5 ( t ) e - ^jtotdt .                                      (1)

-∞

Обратное преобразование Фурье:

∞

5 ( t ) =---- f s ( to ) e ^{j ш} t d rn .                                         (2)

• 2 n

  -∞

Результат преобразования Фурье – амплитудно-частотный спектр, по которому можно определить присутствие некоторой частоты в исследуемом сигнале (рис.4).

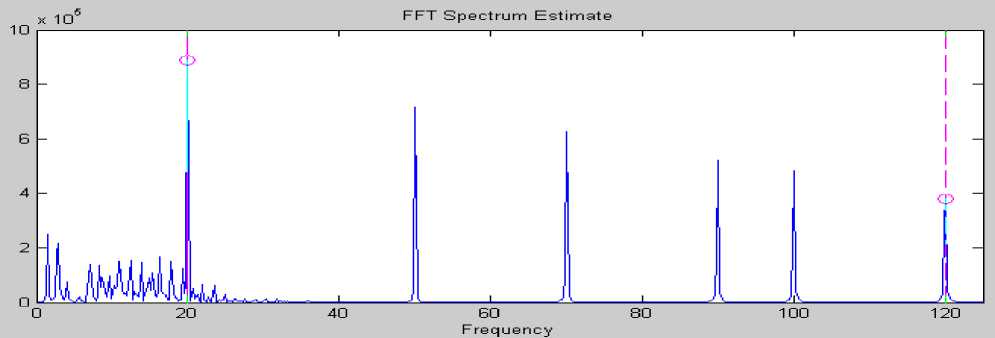
Рис. 4. Фурье-спектр сигнала

Преобразование Фурье имеет ряд недостатков:

• –    исходный сигнал заменяется на периодический с периодом, равным длительности исследуемого сигнала;

• –    со временем плохо работает при изменении параметров процесса (нестационарности), поскольку дает усредненные коэффициенты для всего исследуемого образца;

• –    не дает представления о динамике изменения спектрального состава сигнала.

Рассмотрим три подхода к анализу нестационарных сигналов биогенного происхождения – метод оконного преобразования Фурье, метод вейвлет-преобразования и метод Прони.

Оконное преобразования Фурье. Классическое преобразование Фурье связано со спектром сигнала, взятым во всем диапазоне существования переменной. При анализе нестационарных сигналов интерес представляет только локальное распределение частот, в то время как требуется сохранить изначальную переменную (обычно время). В этом случае используется оконное преобразование Фурье, представляющее собой сегментирование сигнала на фрагменты («окна»). Для начала необходимо выбрать некоторую оконную функцию:

+∞

F ( t, _Ю ) =        J f (t) W ( т - t ) e ' d т ,                          (3)

2 n

-∞ где F(t, о) - распределение частот (несколько искаженное) части оригинального сигнала f (t)

• в    окрестности времени t .

Недостатки оконного преобразования Фурье. Когда нестационарный сигнал имеет высокочастотные компоненты в течение короткого промежутка времени и низкочастотные колебания при рассмотрении больших временных масштабов, оконные преобразования позволяют проанализировать либо высокие частоты в коротком окне времени, либо низкочастотную компоненту, но не оба колебания одновременно (рис.5).

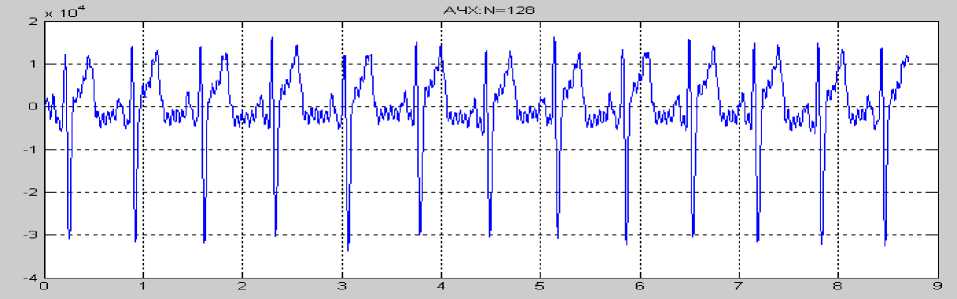
Рис.5. Кардиосигнал после обработки методом Фурье

В результате был разработан подход, при котором для различных диапазонов частот использовались временные окна различной длительности. Оконные функции получались после растяжения-сжатия и смещения по времени гауссиана. Эти базисные вейвлет-функции называются компактными волнами.

Функция v (t) может называться вейвлетом, если она удовлетворяет следующим свойствам:

• –    область определения функции – вся числовая ось;

• -    интеграл от функции v (t) по области определения равен нулю;

• -    функция v (t) быстро убывает при t- ^ ±ro .

На рис.6 изображены примеры простейших базисных функций, посредством которых могут быть представлены произвольные колебания. Вейвлет-разложение по ним проводится путем вычисления сверток сигнала f с компактной волной v при различных масштабах и сдвигах аргумента.

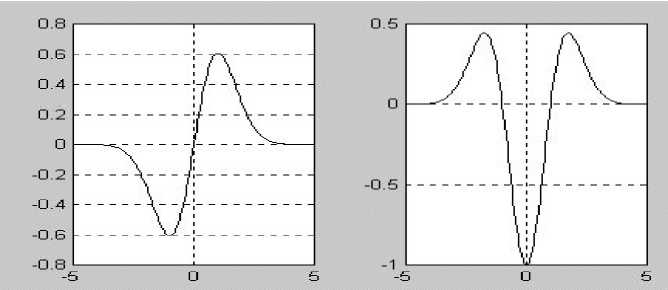
Рис.6. Компактные волны, полученные дифференцированием функции Гаусса

Рассмотрим свертку произвольного сигнала f (t) c функцией:

TO

w ( т , a ) = 1/ a J f ( t ) v ( t -т/ a ) dt,                                (4)

-TO где τ – дрейфовая переменная; а – масштабная переменная.

Результатом свертки является функция, определенная в частотно-временной области, в отличие от преобразования Фурье, которое определено только в частотной области. Таким образом, вейвлет-преобразование позволяет судить не только о частотном спектре сигнала, но также о том, в какой момент времени появилась та или иная гармоника.

Параметр 1/a – частотная характеристика сигнала, подвергшегося вейвлет-преобразова-нию, привязана к «временной точке» – τ . Это означает, что с помощью вейвлет-анализа мы можем изучать сигналы, частотные характеристики которых локально зависят от времени. Фурье-анализ такой возможности не дает.

Как и Фурье, вейвлет-преобразование имеет обратное преобразование, которое записывается формулой:

TO TO f (x) = g J Jv(x — t/a)w(t,a)da/a2 dt,                           (5)

-to 0

где g – некоторая константа [5].

Вейвлет-преобразование Добеши (рис.7).

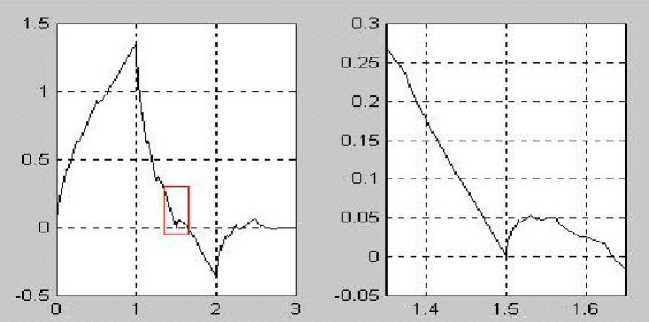
Рис.7. Структура вейвлета Добеши

( С о   С 1

С 3 — С 2

С2   С3    ..

С1 - Со   ..

С0  С1  С2

A

С 2   С 3

l С 1 - С о

С 0

С 3

С 1

- C2

С 2

С 1

С 0

С 3

С 3

- С о С 1

- С 2 J

– матрица Добеши.

Преобразование Добеши от некоторого вектора соответствует умножению его на матрицу.

Каждая строка матрицы соответствует свертке вектора сигнала с локализованным вейв-лет-фильтром. При этом нечетные строки сглаживают, а соответствующие четные фильтры вычисляют поправки к сглаживанию, обеспечивая обратимость преобразования. Коэффициенты C0 ...C3 могут быть выбраны так, чтобы поправки обращались в нуль для гладких функций. За- нуление свертки с постоянной и линейной функциями дает два условия на неизвестные коэффициенты:

C 3 - C 2 + C 1 - C 0 = 0

0 С 3 - 1 С 2 + 2 С 1 - 3 С ₀ = 0 .

Далее потребуем, чтобы преобразование было ортогональным – обратное преобразование получалось простым транспонированием. Из условия равенства произведения матриц прямого и обратного преобразования единичной матрице получаем еще два условия [4]:

c ² ₀ + c ²1 + c ² ₂ + c ² ₃ = 1        ^     c ₀ = ( 1 + Vs ) /4V2          c ₂ = ( 3 - Vs ) /4V2

C ₂ C ₀ + C ₃ C 1 = 0         Откуда       C 1 = ( 3 + V3 ) MV2         C 3 = ( 1 - V3 ) /4^ .

Полное вейвлет-преобразование получается путем умножения вектора сигнала на полученную матрицу Добеши, далее нечетные компоненты сигнала (сглаженная версия сигнала) снова умножаются на матрицу Добеши (вдвое меньшей размерности), и так до тех пор, пока не будет получено полностью сглаженное представление, т.е. среднее значение сигнала (рис.8–9).

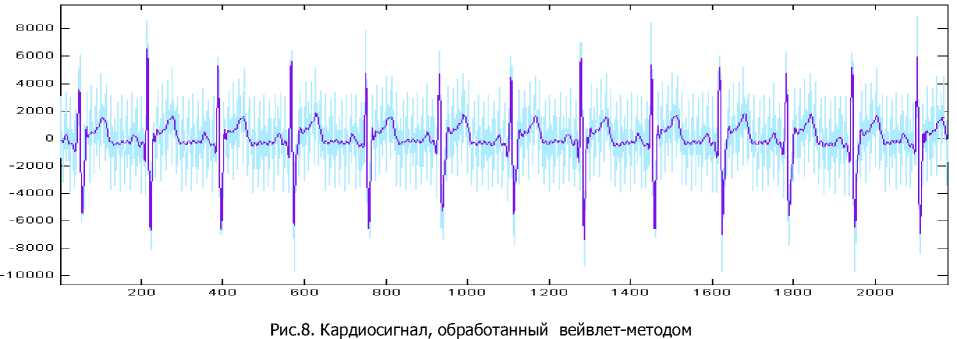
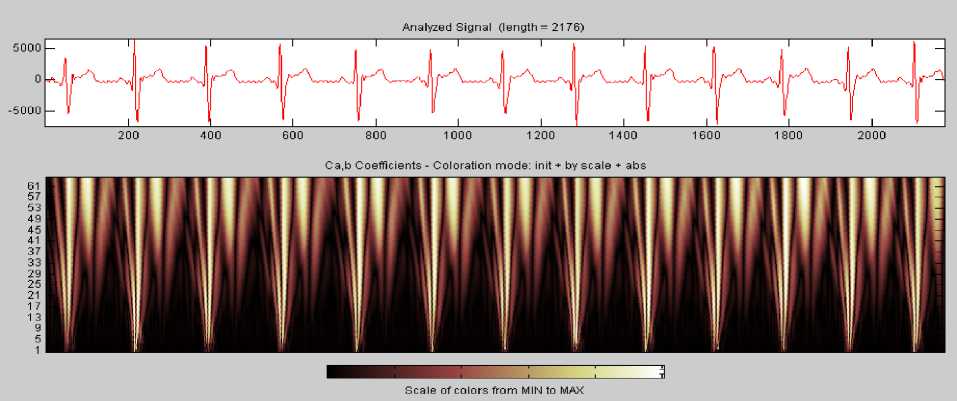
Рис.9. График кардиосигнала и спектрограмма

Исходный подход Прони. Если число используемых отсчетов данных равно числу экспоненциальных параметров, то возможна точная подгонка экспонент под имеющиеся данные. Рассмотрим функцию дискретного времени, представляющую собой сумму р -экспонент:

* п ] =тм^а .

к =1

Заметим, что в этом выражении используется х[n], а не ~ [n], поскольку точно 2р-ком плексных отсчетов х[1], ..., х[2р] используется для точной подгонки к экспоненциальной модели с 2р-комплексными параметрами h1, …,hp, z1 ..., zp. в матричной форме:

Входящие в р -уравнения (6) можно записать

p z ?..	- zp	1	Г h 1
z 1 z 2 ...	....z 1 p		h 2

1  Г ^{x [1]} )

x [2]

V               у

Матрица с временными индексами элементов z имеет структуру матрицы Вандермонда. Если может быть найден метод для раздельного определения элементов z , то уравнение (7) можно рассматривать как систему уравнений, решив которую, определяют неизвестный вектор комплексных амплитуд.

Ключ к разделению основан на том факте, что уравнение (7) является решением некоторого однородного линейного разностного уравнения с постоянными коэффициентами. Для того чтобы определить вид этого разностного уравнения, определим сначала полином ф ( z ) , корнями которого являются экспоненты z k :

p ф ( z) = П (z - zk ) .                                     (8)

к = 1

Если произведения в (13) выразить в виде степенной последовательности, то полином можно представить в следующем виде:

p

ф ( z ) = Х a[m ] z p — m ,                                       ⁽⁹⁾

m = 0

с комплексными коэффициентами a [ m ], для которых a [0]=l.

Осуществляя в уравнении (6) сдвиг индекса от n к ( n–m ) и умножая обе его части на параметр a [ m ], получаем

p

a [ m ] x [ n - m ] = a [ m ] ^ h_kz n ^{- m - 1} .                            (10)

к = 1

Записывая аналогичные произведения а [ 0 ] x [ n ] , ,„,а [ m - 1 ] х [ n-m+1 ] и осуществляя суммирование, получаем: p       pp

^ a[ m] x[ n - m] = ^ h ^ a[ m] zn - m-1 ,(11)

m = 0                   i = 0 m = 0

которое справедливо при р+ 1 < n <  2 р . Получаем:

ppp

^a[m]х[n - m] = ^htzn-p ^ a[m]zip-m-1 = 0 .(12)

m=0                  i=0

Сумму в правой части (12) можно рассматривать как полином, определяемый уравнением (9), который записан через свои корни, что и обеспечивает в уравнении (12) равенство нулю. Уравнение (12) – это линейное разностное уравнение, однородное решение которого выражается формулой (6). Полином (9), ассоциированный с этим линейным разностным уравнением, называется характеристическим.

Можно записать в виде следующего рxр -матричного уравнения р -уравнения, представляющие истинные значения коэффициентов а [ n ] , удовлетворяющих (12):

Г x [ p ] x [ p - 1]......	.......x [1] J	Г a [1] ^		Г x [ p + 1]
x [ p + 1] x [ p ]......	.......x [2]	a [2]		x [ p + 2]

( x [2 p - 1] x [2 p - 2]... x [ p Ц a[p ] J   ( x [2 p ] J

Из уравнения (13) следует, что, имея 2 р -отсчетов комплексных данных, возможно разделение множеств параметров h k и z k . Комплексные полиномиальные коэффициенты а [1], ..., а [ р ], которые являются функциями только зависящих от времени компонентов z k экспоненциальной модели, позволяют по временным отсчетам сформировать соотношения для линейного предсказания. Матрица в уравнении (13) имеет тёплицеву структуру [3].

Процедуру Прони для подгонки р- экспонент к 2 р- отсчетам данных можно теперь представить в виде следующих трех этапов.

На первом этапе получается решение уравнения (13) для коэффициентов полинома.

На втором этапе вычисляются корни полинома, определяемого уравнением (9). Используя корень zi можно определить коэффициент затухания a i и частоту синусоиды f i с помощью соотношений:

a i = ln | z i |/ T ( c - 1 ) ,                                               (14)

f i = arctg[Im { Z i } /Re { Z j } ]/2 n T ( Гц ) .                             (15)

Для завершения процедуры Прони корни полинома, вычисленные на втором этапе, используются далее для формирования элементов матрицы уравнения (7), которое затем решается относительно р комплексных параметров h [1],  , h [ р ]. Каждый параметр h i используется далее для определения амплитуды A i и начальной фазы θ i , которые вычисляются с помощью вариаций

A i = h i | ,                                                      (16)

9 i = arctg[Im { h i } /Re { h i } ] (рад).                              (17)

Результаты вычислений показаны на рис.3, 10–11.

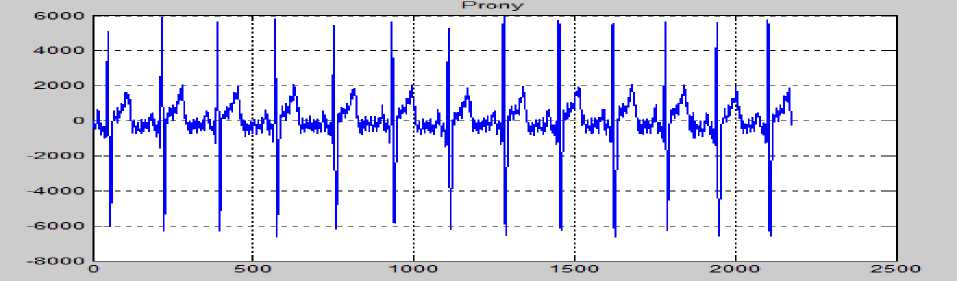
Рис.10. Кардиосигнал, обработанный методом Прони (сумма комплексных экспонент)

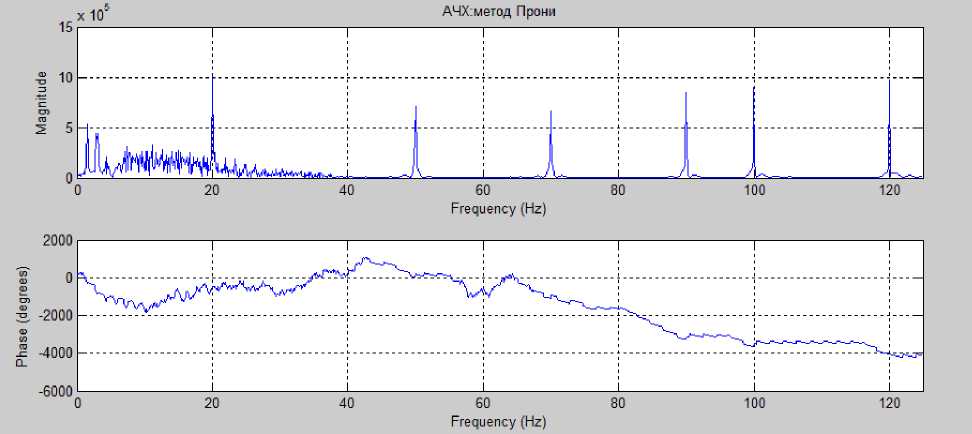
Рис.11. Спектр сигнала и фаза после анализа методом Прони

Метод наименьших квадратов Прони. Н а практике число отсчетов данных N , как правило, превышает то минимальное их количество, которое необходимо для подгонки модели из р -экспонент, т.е. N > 2p . В этом переопределенном случае последовательность отсчетов данных может быть аппроксимирована лишь как экспоненциальная последовательность:

p

~ [ n ] = ^ h k z n - 1 , где 1 < n < n.                               (18)

k = 1

Ошибка аппроксимации в данном случае распределяется выражением е [ n ] = x [ n ] - ~[ n ] . Одновременное нахождение порядка р и параметров { h k , z_k }, где 1 < k

, которые минимизируют сумму квадратов ошибки и представляет собой трудную нелинейную задачу:

N

Р = Е^[n]|2 .                                          (19)

n=1

Используя вариант метода Прони можно определить субоптимальное решение, которое обеспечивает удовлетворительные результаты. Используя на первом и втором этапе трехэтапного метода Прони соответствующие линейные процедуры наименьших квадратов, получим процедуру экспоненциального моделирования, которую иногда называют обобщенным методом Прони [3]. Выводы. Применены хорошо разработанные методы Фурье с помощью дискретного преобразования Фурье (ДПФ), использовался алгоритм быстрого преобразования Фурье (БПФ), вейвлет-преобразование и метод Прони для анализа и параметризации нестационарных сигналов. Проведена оценка погрешности и сравнительный анализ полученных результатов.

На основе результатов анализа ЭКГ человека показано, что вейвлетные базисы могут быть хорошо локализованными как по частоте, так и по времени. При выделении в сигналах хорошо локализованных разномасштабных процессов можно рассматривать только те масштабные уровни разложения, которые представляют интерес.

Вейвлетные базисы, в отличие от преобразования Фурье, имеют достаточно много разнообразных базовых функций, свойства которых ориентированы на решение различных задач. Базисные вейвлеты могут иметь и конечные, и бесконечные носители, реализуемые функциями различной гладкости.

Использование метода Прони позволяет получить более точные спектральные оценки для коротких последовательностей данных. Указанные возможности позволяют получить новую информацию о динамике изменений ЭКГ в процессе деятельности человека.