Применение векторного формализма в логике и логико-математическом моделировании
Автор: Аршинский Л.В.
Журнал: Онтология проектирования @ontology-of-designing
Рубрика: Методы и технологии принятия решений
Статья в выпуске: 4 (22) т.6, 2016 года.
Бесплатный доступ
В статье выполнен обзор ряда направлений, посвящённых применению векторного формализма в логических исследованиях. Выделяются три таких направления. Первое связано с усложнением формального аппарата классической математической логики за счёт векторизации категорий Истины и Лжи. Оно представлено векторной логикой Е. Мизрахи и матричной логикой А. Штерна. Второе основано на векторизации логической семантики. В нём истинность рассматривается как многокомпонентный вектор. Здесь отмечены логика К.И. Бахтиярова, нейтрософская логика Ф. Смарандаке и логики с векторной семантикой. Третье направление связано с векторизацией силлогистики Аристотеля. Векторное представление в последнем случае используется для частичной визуализации и автоматизации построения силлогизмов. Все три направления имеют практическое значение и находят применение, в частности, для решения задач в области вычислительной техники и искусственного интеллекта.
Неклассическая логика, векторная логика, логики с векторной семантикой
Короткий адрес: https://sciup.org/170178732
IDR: 170178732 | УДК: 510.64+004.89 | DOI: 10.18287/2223-9537-2016-6-4-436-451
Текст научной статьи Применение векторного формализма в логике и логико-математическом моделировании
Если в развитии логики как науки выделять наиболее значимые этапы, невозможно обойти два из них: собственно создание логики как таковой Аристотелем и её математизацию Дж. Булем. Это начало и конец её первого «диалектического витка», называемого классической логикой. Математизация привела к формированию двух основных направлений её дальнейшего развития. Первое связано с развитием и усложнением формального аппарата классической логики. Второе - с отрицанием классической логики и появлением целого сонма логик, которые в совокупности носят название «неклассических». Причина проста: математика ввела в логику понятие числа. Это естественное, более того, ключевое для математики понятие привело, с одной стороны, к стремлению ввести в обращение более сложные объекты числовой природы, с другой, как ни странно, - к отрицанию постулатов, положенных Аристотелем в основание логической науки.
Число в виде двух логических констант: 1 - «Истина» и 0 - «Ложь», - появилось в логике трудами Г. Фреге и Ч. Пирса [1-3]. Их размышления, в первую очередь выполненный Г. Фреге логический анализ языка, выпустили джинна, который похоронил представление об аристотелевской логике, как единственно верной логической картине мира. Безусловно, введение числовых значений истинности не оказало бы столь «роковых» последствий, если бы сама эта логика исчерпывающим образом описывала мир. Уже сам автор понимал её ограниченность, утверждая применимость этой науки только для physis'а - неизменной основы ми- ра и отрицая её полезность для «диалектических высказываний», зависящих от места, времени, знаний и ощущений человека [4]. Он же сформулировал и проблему истинности суждений о будущих случайных событиях; проблему, приведшую Я. Лукасевича к идее сначала трёхзначной, а впоследствии k- и континуумзначных логик [5]. Пока логика действовала лишь в терминах утверждения и отрицания, как это было у Аристотеля, у неё не было подходящих выразительных средств, чтобы эффективно описывать неполное, неточное, относительное, противоречивое и т.д. знание. Это средство ввела математическая логика, и этим средством оказалось число. Введённые Ч. Пирсом и Г. Фреге понятия Истины и Лжи, как значения истинности предложений, успешно превратились в пару {1, 0}. И после этого стало ясно, что новые области, о которых не могла и потому отказывалась рассуждать классическая логика, могут быть охвачены введением дополнительных значений истинности: %, %, m/n и т.д., вплоть до непрерывного отрезка [0, 1] либо его аналогов. При этом в терминах числа были переформулированы принципы противоречия и исключённого третьего, и оказалось, что они могут не выполняться [5]. Это и стало концом классической логики как «единственно верного учения».
Другим следствием математизации логики стало внесение в неё идей, которые прежде казались с ней несовместимыми. Речь идёт об использовании математического аппарата, который создавался для решения совсем иных задач. В первую очередь физики и механики. Математизация прошла путь от простейшего оперирования парой чисел {1, 0}, через многозначность, к векторам, позволяя отразить более сложные взаимоотношения объектов и понятий внешнего мира. Считается, что одним из первых о возможной многомерности логики заговорил в начале XX в. казанский логик Н.А. Васильев [6]. Однако в его работах этот термин употребляется скорее как метафора. Фактически речь в них шла о многозначной логике, если пользоваться современной терминологией. Сам Н.А. Васильев не пользовался понятием числа и, развивая свои взгляды, говорил о необходимости замены логического квадрата логическим треугольником, а в качестве дополнительного значения истинности вводил Противоречие [7]. Возможно этим объясняется то, что в то время его идеи развития не получили, а многозначность вошла в логику трудами других исследователей. Однако высказанное им представление о многомерности, пространственности логики тесно связано с понятием вектора. И в этом смысле вклад Н.А. Васильева существенен.
В данной работе выполнен обзор ряда работ и направлений, связанных с применением векторного формализма в логических исследованиях и соответствующих прикладных задачах.
1 Векторная логика Мизрахи и матричная логика Штерна
Среди логик, использующих понятие вектора для представления истинности, следует отметить векторную логику Мизрахи ( Mizraji E. ). В ней векторами формализуются значения Истина и Ложь . Её появление связано с исследованиями в области моделирования контекстно-зависимой памяти в нейронных сетях [8, 9]. В основе формализма лежит представление Истины и Лжи двумя q -мерными вектор-столбцами ( q > 2) единичной длины: s и n . Первый ассоциируется с Истиной , второй с Ложью . Истинность в целом представлена парой { s , n }. Вектор-столбцы s и n ортонормальны:
s n = ns = 0 ; s s = n n = 1.
Для определения логических связок применяются «монадные операторы»:
I = ss r + nn r ;
N = ns r + sn r ;
K = ss T + sn T ;
M = ns T + nn T .
Матрица I - оператор тождества; для него выполняется свойство: Ip = p , где p - произвольный вектор. Матрица N соответствует отрицанию: Ns = n и Nn = s .
Конъюнкция и дизъюнкция представляются операторами C и D соответственно:
C = I ® s T + M ® n T ;
D = K ® s T + 1 ® n T .
Или, что то же самое:
C = s(s ® s) T + n(s ® n) T + n(n ® s) T + n(n ® n) T ;
D = s(s ® s) T + s(s ® n) T + s(n ® s) T + n(n ® n) T .
Здесь ® - произведение Кронекера: если A = [ ay ] и B = [ by ] - пара матриц размерностью m x n и p x q , то A ® B = [ ay B] .
Понятие нечёткости автор вводит конструкцией: p = y s + ( 1 - У )n , где y е [ 0,1 ] [10]. В частном случае векторов s = ^ 1 ^ и n = ^ ^ ^ это представление фактически совпадает с традиционным.
Несмотря на определённое обобщение классической и нечёткой логик, в логике Мизрахи используются только известные логические связки: конъюнкции, дизъюнкции, отрицания и т.д. Принципиально новым тут является переход от логических констант {Истина, Ложь} к векторам Истины и Лжи. Далее автор развивает это направление, формализуя в нём модальности необходимого и возможного, а также проводя аналогии с вероятностной логикой [10, 11]. Среди российских работ в этой области можно указать [12]. В ней с позиций векторно-матричного представления развита логика нечётких предикатов и дан пример решения экономической задачи. Данная работа, по словам её авторов, опирается на идеи Мизрахи. Интересно, что в ней авторы рассматривают логику Мизрахи с более общих позиций, называя её тензорной.
Близкой по духу к логике Мизрахи является появившаяся примерно в то же время матричная логика Штерна (Stern A. ) [13]. Её любопытной особенностью является настойчиво проводимая параллель с квантовой механикой, вплоть до использования специфической терминологии. Например, истинность в ней описывается «бра»- и «кет»-векторами - это термины, пришедшие в квантовую механику из работ П. Дирака. Одно из прикладных направлений этой логики - моделирование квантовых процессов.
В логике Штерна в терминах бра- и кет-векторов, а также матричных операторов, подобных операторам квантовой механики, описываются все известные в классической математической логике логические связки: конъюнкции, дизъюнкции, исключающего или, отрицания, эквивалентности, импликации, стрелки Пирса и пр., - исследуются и обобщаются базовые логические законы вроде законов противоречия, исключённого третьего, Де Моргана. С позиций матричной логики обсуждаются логики Лукасевича, Поста, Рейхенбаха, рассматривается формализация истинности комплексными числами. В частности, известная в нечёткой логике взаимосвязь: a ++ а -= 1, где a += || а || е [0,1] - истинность утверждения a , а а - = || ^ a | е [0,1] - истинность его отрицания, формирующая, если можно так выразиться, линейную функцию перехода от вектора Истина ^ 1 ^ к вектору Ложь ^ ^ ^ , заменяется функцией перехода «по дуге» единичного радиуса (см. рисунок 1). В связи с этим в [13] говорится
— a

0 а + 1
Рисунок 1 - Переход от вектора Истина к вектору Ложь при нечётком и матричном представлении истинности.
о фазовом пространстве значений истинности. Подобную же трактовку истинности допускает и логика Мизрахи. В целом обе этих логики рассматриваются как алгебраические модели элементарной логики, основанные на матричной алгебре. Пионерной работой по приложению линейной алгебры к формальной логике в [9] называется [14].
Следует отметить, что в [13] в качестве базис-1 0)
ных векторов берутся только I о I и I 1 I .
Е. Мизрахи идёт дальше, допуская произвольное количество и произвольные значения компонентов для s и n при соблюдении требования их ортоно-мальности. И в том и в другом случае привязка к категориям Истины и Лжи и ортонормальность базисных векторов выглядит как скрытая
реализация принципов противоречия и исключенного третьего, что позволяет рассматривать эти логики как развитие классических представлений.
Обращает на себя внимание и достаточно тяжелый в содержательном плане математический аппарат обеих логик.
2 Логика Бахтиярова
Примером, где понятие вектора истинности связано с развитием неклассических взглядов, являются исследования К.И. Бахтиярова [15-17]. В их основу положена идея о том, что суждение может оцениваться с разных сторон (позиций, аспектов). Причём истинность каждого аспекта принимает одно из трёх значений: +1 (Истина), - 1 (Ложь), 0 (Неопределённость). Истинность суждения в целом представляет собой вектор, компоненты которого суть аспекты оценивания, значения которых принадлежат множеству { - 1, 0, +1}. Истинность сложных суждений рассчитывается на основе покомпонентной обработки векторов. При этом для дизъюнкции результирующее значение аспектов вычисляется по формуле
||а 1 v а2||i = sign(||а 1||, + ||а2||, + 1), а для конъюнкции - по формуле
|| а 1 & а 2 || i = sign (|| а 1 || i + || а 2 || i - 1).
Для импликации используется
||а 1 ^ а2||i = sign(||а2||i - ||а 1||i + 1), для отрицания - формула
|Ь а || i --|| а || i .
1, если x > 0;
0, если x < 0.
Здесь || а || i - i- й аспект истинности суждения а ; sign ( x ) =
Таким образом, семантика Бахтиярова основана на многоаспектности и векторном описании истинности. Сами аспекты принимают три возможных значения: - 1, 0, и 1.
3 Нейтрософская логика Смарандаке
Интересным логическим формализмом, использующим векторное представление истинности, является нейтрософская логика Смарандаке (Smarandache F.). Она опирается на идею, что истинность любого суждения есть вектор из трёх компонентов Каждый из компонентов вектора истинности в логике Смарандаке принимает значение из нестандартного интервала | 0,1+[, где -0 = 0 - £, 1+ = 1 + £ при £ ^ 0 . Никакой функциональной связи между T; I; F нет, так что -0 < T +I + F< 3+. В прикладных задачах нестандартный интервал можно заменять обычным: [0,1]. Тогда T, I, F е [0,1] и 0 < T +I + F< 3 [19, 20]. Значения компонентов могут быть представлены как числами (назовём их «точечными»), так и интервалами, а также представлять собой упорядоченное подмножество из ]-0,1+[ (или [0,1] в прикладных задачах). Логические связки конъюнкции, дизъюнкции, отрицания представляются в ней конструкциями [20] || а1 & а2 ||= (T • T2;I 1 • I2; F[ • F2 ) , || а1 v а 2 ||=< T1 +T2 -T1 • T2;11 +I 2 -11 • I 2; FI + F2 - FI • F2 ) , || ^а || 1' T ;1+-1 ;1+- F> соответственно. Здесь «•», «+», «-» - операции умножения, сложения и вычитания, обобщённые на нестандартные подмножества интервала ]-0,1+[; T, I, F, - значения компонентов векторов истинности: || а1 ||= Интересно отметить, что в более поздней работе [21] логические связки формализуются иначе: || а1 & а2||= <mm(T, T2);max(11,12);max(F(, F2)), || а v а2 ||= <max(T, T2);min(11,12);min(F1, F2)>, || ^а ||=<F;1+-1; T>. Здесь, как и в первом случае, min() и max() - обобщения функций минимума и максимума на подмножества нестандартного интервала ]-0,1+[. Внимательный анализ показывает, что это принципиально разные определения связок. Автор вводит разные типы конъюнкции, дизъюнкции и отрицания, не комментируя этого. В прикладных задачах между суждениями важно задавать порядок, позволяющий предпочесть одни другим. В классике эта проблема не рассматривается, ложные предложения просто исключаются из рассмотрения. Однако в многозначных логиках, где результатом вывода часто является несколько утверждений с разными значениями истинности, упорядочивать суждения необходимо. В логике Смарандаке для этого пользуются правилом [20]: а 1 < а2 (а 1 менее предпочтительно, чем а2), если и только если T1 < T2,11 > 12, F 1 > F2, для точечных компонентов, и а 1 < а2, если и только если inf T1 < inf T2, sup T1 < sup T2, inf 11 > inf 12, sup 11 > sup 12, inf F 1 > inf F2, sup F 1 > sup F2 для компонентов-подмножеств. В [18], а также [20, 21] с позиций нейтрософской логики проведён анализ известных логических (и не только) представлений, включая теорию множеств (нейтрософские множества), теорию вероятности (нейтрософская вероятность), статистику, геометрию и т.д. В частности, рассматривая нейтрософию как направление философии, автор затрагивает квантовомеханическую и релятивистскую картины мира. На русском языке основы этой концепции представлены в [18] и [22]. Нейтрософская логика является следующим шагом после нечёткой. Её особенностью служит ограничение на число компонентов вектора истинности при их жёсткой содержательной интерпретации: Истина, Ложь, Нейтральность. Также используется классический набор логических связок и единственный критерий частичного порядка между суждениями. Достаточно интересным выглядит переход от привычного интервала значений истинности [0,1] к нестандартному | 0,1+[, хотя прикладная ценность такого перехода всё же сомнительна. В [23] дан пример решения практической задачи с использованием описанного представления.
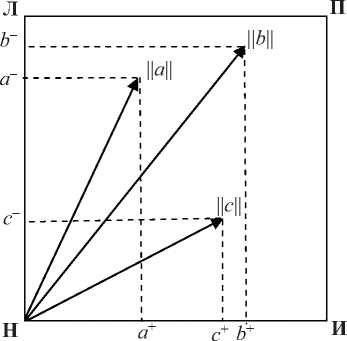
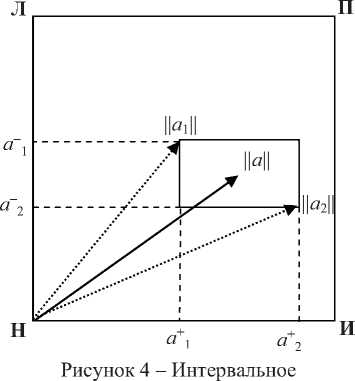
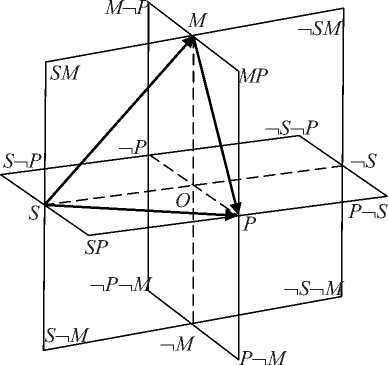
4 Логики с векторной семантикой 4.1 Основные понятия 4.2 Сложные суждения Логики с векторной семантикой - класс логик, в которых истинность суждения а формализуется вектором с произвольным (в общем случае) числом компонентов: ||а|| = (а 1; а2;.; а ), а е [0, 1]. Значения каждого из компонентов определяются своим комплексом свидетельств. Позиции компонентов в векторе называются аспектами истинности, а их значения - значениями этих аспектов [24]. Содержательная сторона аспектов вторична. Важно, что истинность отражает представление о соответствии суждения реальности. Важен также характер влияния отдельного компонента на это соответствие. В этом смысле, каковы бы не были аспекты истинности, все они делятся на два класса. В первом случае истинность, выраженная вектором (а 1; а2;...; а1;...; а"), говорит о большем соответствии, чем (а 1; а2;...; а ;.; а ), если а > а . Во втором - если а1< а1 [25]. Иначе говоря, важно, что рост (убывание) аспектов первого и второго типа влияет на истинность взаимно противоположным образом. Аспекты первого типа названы позитивными, а второго - негативными. Чтобы их различать используются верхние индексы «+» и «-». Например, (а+; а-\ (0.5+; 0.2+; 0.9-) и так далее. Если порядок следования аспектов в векторе таков, что сначала указываются позитивные компоненты, такая запись называется нормальной формой вектора истинности: (а1+; а2+;., а1 +; а (1+1)-;.;а" ). Количество позитивных и негативных компонентов в общем случае может быть любым. При этом, если содержательный смысл аспектов истинности не важен и их число не оговаривается, то говорится о многоаспектных векторных логиках (V"-логиках). Иначе, о двухаспектных , трехаспектных и т.д. Если существенна содержательная сторона аспектов, это может быть отражено в наименовании. Например, VTF-логика - это двухаспектная векторная логика с аспектами (Истина; Ложь). Для построения сложных суждений в логиках с векторной семантикой рассматриваются следующие типы логических связок: 1-я и 2-я форма конъюнкции, 1-я и 2-я форма дизъюнкции и две формы отрицания [24]. Определение 1. Первой формой конъюнкции двух суждений а и У называется суждение c = а & У, значения аспектов истинности которого определяются по правилу: У = а1 • У, если аспект позитивный; c = а1 © У, если аспект негативный. Определение 2. Второй формой конъюнкции а и У в называется суждение c = а &2У, значения аспектов истинности которого определяются по правилу: c = а1 • У. Определение 3. Первой формой дизъюнкции двух суждений а и У называется суждение c = а v У, значения аспектов истинности которого определяются по правилу: c = а1 © bl, если аспект позитивный; c = а1 • у, если аспект негативный. Определение 4. Второй формой дизъюнкции двух суждений а и У в называется суждение c = а v2У, значения аспектов истинности которого определяются по правилу: cl = а © У. Первые формы - это обобщения классических конъюнкции и дизъюнкции на векторный случай. Вторые возможны только в векторной семантике. Здесь x • y - t-норма, x © y - t-конорма (5-норма) в инфиксной записи при том, что между ними существует взаимосвязь: (1 - x) •(l-y) = 1 - x © y; (1 - x) ©(1 -y) = 1 - x • y. Примерами здесь служат пары функций x • y = min(x, y), и x ©y = max(x, y); x • y = max(0, x + y - 1), и x © y = min(1, x + y); x • y = xy, и x ©y = x + y -xy. Определение 5. Первой формой отрицания (отрицанием в форме перестановки) называется суждение —iа, истинность которого получается из ||а|| путём перестановки местами значений позитивных и негативных компонентов (позитивные компоненты объявляются негативными, а негативные позитивными). Например, для VTF-логик это выглядит как ||^а|| = (а-; а+). Эта форма отрицания привязана к содержательному смыслу аспектов истинности и потому применима не для всех векторов истинности. Определение 6. Второй формой отрицания является отрицание в форме дополнения: ||~а|| = (1 - а 1; 1 - а2;...; 1 - а”). Для этой формы отрицания выполняются законы де Моргана в виде: ||~(а v У)|| = ||~а & ~У||; ||~(а & У)|| = ||~а v ~У||; ||~(а V2 У)|| = ||~а &2 ~У||; 4.3 Кванторы всеобщности и существования 4.4 Отношения между суждениями Кванторы всеобщности и существования также приобретают две формы. Их первая форма определяется первой формой связок конъюнкции/дизъюнкции по всем значениям предметной переменной, вторая форма - второй формой связок [26]. Между суждениями в логиках с векторной семантикой можно устанавливать отношения, аналогичные отношениям импликации и эквивалентности в классической логике [20]. Определение 7. Суждение а сильнее суждения b (а доминирует над b, записывается а >> b), если а > у для всех i; т.е., если значения всех аспектов вектора ||а|| не меньше значений соответствующих аспектов вектора ||b||. Соответственно, суждение а слабее суждения b (b доминирует над а, записывается а<< b), если а1< bi для всех i; т.е., если значения всех аспектов вектора ||a|| не больше значений соответствующих аспектов вектора ||b||. Определение 8. Суждение а правдоподобнее суждения b (записывается а > b), если а1 > bi для всех позитивных аспектов, а1 < bi для всех негативных аспектов, т.е., если все аспекты вектора ||а|| «не хуже» соответствующих аспектов вектора ||b|| в «логическом» смысле. В свою очередь, суждение а менее правдоподобно, чем суждения b (записывается а< b), если а1< bl для всех позитивных аспектов, 4.5 Логический вывод а1 > у для всех негативных аспектов, т.е., если все аспекты вектора ||а|| «не лучше» соответствующих аспектов вектора ||b|| в «логическом» смысле. Данные отношения называются отношениями доминирования и правдоподобия. Определение 9. Суждение а логически эквивалентно суждению b (а = b), если а< b и а > b (а также а<< b и а >> b). В любом из этих случаев а1 = bl для всех i. Аналогия между отношениями правдоподобия и доминирования и классической импликацией позволяет ввести аналоги правила modus ponens [24, 25]: а, а<< b Р b: || b || = ||а|| ^<1;^; 1); а, а< b Р b: ||b|| = ||а|| :(!';...; 1+; 0”,^, 0 ). 4.6 VTF-логики Запись после двоеточия оговаривает область возможных значений вектора истинности заключения b: ||b|| е [а1, 1] х [а2, 1] х_х [ап, 1] в первом случае и ||b|| е [а1+, 1] х [а2+, 1] х...х [а+, 1] х [0, а(1 'п ] х [0, а(1 '2| ] х...х [0, ап”] во втором (здесь учитывается наличие позитивных и негативных аспектов). Ещё один вид логического вывода, который отчасти может быть обобщён на вектор произвольной размерности, рассматривается в связи с VTF-логиками. Наиболее изученным классом логик с векторной семантикой являются двухаспектные векторные логики с аспектами <Истина; Ложь) [24, 25]. Они наиболее близки к таким практически востребованным формализмам, как классическая и нечёткая логики (являются их обобщением), а также обобщают некоторые паранепротиворечивые (например, логику Данна [27]). Рисунок 2 - Графическое представление вектора ||a|| = (a+; a-) Для этого класса логик ||a|| = (a+; а)_ где а+ - мера того, что суждение a есть Истина, a-- мера того, что оно есть Ложь. Меры Истины и Лжи в общем случае устанавливаются независимо друг от друга, каждая по своему комплексу свидетельств. Истинность суждения в этом случае может быть проиллюстрирована рисунком 2. Здесь Н представляет значение истинности неопределённого суждения с вектором (0; 0); Л - строго ложного суждения (0; 1); П -полностью противоречивого суждения (1; 1); И -строго истинного суждения (1; 0). Если a и b два атомарных суждения, то для VTF-логик первая и вторая форма дизъюнкции, конъюнкции и отрицания определятся следующим образом: ||a vb||=(a+©b+; a • b ); ||a v2b||=(a+©b+; a © b ); ||a & b||=(a+• b+; a-© b-); ||a &2 b||=(a+• b+; a"•b-); ||^a||=(a-; a+); ||~a||=(1 - a+; 1 - a-). Первые формы конъюнкции и дизъюнкции здесь - это обобщения классических конъ юнкции и дизъюнкции на векторный случай. Вторые существуют только в векторной семантике. Первая и вторая формы отрицания при переходе к классической и нечёткой семантике дают одну и ту же форму отрицания: классическую или нечёткую. В VTF-семантике эти отрицания, как легко видеть, различаются. Первое - это отрицание в смысле перестановки свидетельств (позитивные меняются с негативными), второе - отрицание в силу недостатка информации. Рисунок 3 - Иллюстрация отношений правдоподобия и доминирования для VTF-логик: a<< b, c<< b, a< c. Справедливы свойства: -i(a v b) = ^a & ^b; Отношения правдоподобия и доминирования иллюстрируются рисунком 3. Выполняются соотношения: a< a v b; a & b< a; a<< a v2b; a &2b<< a. Логический вывод в VTF-логиках, помимо упомянутого выше, может выполняться с использованием следующих двух правил, аналогов классических modus po-nens (MP) и modus tollens (MT): a, a ^ b p b: ||b|| = ||a & i|| = (a+• i+; a-© i) ^(1; 0); ^b, a > b p^a: ||^a|| = ||^a & i|| = (a- • i+; a+© i-) ^ (1; 0). Здесь a ^ b - импликация «Если a, то b» - характерная единица знаний многих экспертных систем. В них она обычно рассматривается как неделимое целое. Её истинность задаётся экспертом, что естественно для таких задач: ||a ^ b|| = ||i|| = (i+; i). Указанные правила вывода обобщаются на интервальное представление истинности (рисунок 4) [28]. Обобщение MP выглядит следующим образом. Если истинность малой посылки есть ||a|| = ||a||i ^ ||a||2 = <[a+i, a+2]; [a 2, a 1]), а истинность большой - ||i|| = ||A\i - ||i||2 = <[i+i, i+2], [i-2, iA]), представление вектора ||a|| = ||a||i + ||aЦ2 = <[a+baД]; [a"2, a"J) то истинность заключения || b || равна ||b|| = <a+i • i+i; a-i © i-i) + <a-i © i+2; a+i • i2) = = <[a +i • i+i, a-i © i+2]; [a +i • i2, a-i © i-i]), или a, a > b p b: ||b|| = ||a & i|| = = <a+i• i+i; a-i© i-i) ^ <a-i© i+2; a+i• i2). Иначе говоря, ||b|| e [a+i• i+i, a-i© i+2] x [a+i• i-2, a-i© i-i]. В свою очередь MT для первой формы отрицания обобщается на интервалы как ^b, a ^ b I—1 a: ||^a|| = ||^b & i|| = <b-i• i+i; b+i© i-i) ^ <b+i © i+2; b-i • i-2), или, что то же самое, ||a|| = <b-i • i-2; b+i © i+2) + <b+i © i-i; b-i • i+i). Для второй формы отрицания (отрицания в форме дополнения) правило МТ в интервальном случае приобретает вид [29] ~b, a ^ b |~a: ||~a|| = <(i - b+2) • i+i; (i - b-2) © i-i) ^ <(i - b+2) © i+2; (i - b-2) • i-2). Суждения в VTF-логиках могут характеризоваться рядом скалярных мер: • мера определённости (определённость) ро(a) = a+© a; • мера противоречия (противоречивость) //п(a) = a+• a-; • показатель достоверности (достоверность) рд(a) = a+- a-; • мера строгости (строгость) рс( a) = ро( a) - рп( a) = a+©a- - a+•a-или рс( a) =|дц (a )|; • показатель избыточности (избыточность) ^изб(a) = a + a- - i. В интервальном случае в качестве a+ и a-можно брать середины интервалов или определённую точку внутри них. Кроме того в интервальном случае также может быть также введена мера точности вектора истинности, которая должна быть максимальной, когда a+i = a+2 и a-i = a-2 и минимальной при ||a|| = <[0, i]; [0, i]). Такую роль может исполнять, например, показатель Втчн = i ( a 2+ — a i ) + (a 2 — a i ) 2 Механизм интервального вывода для VTF-логик описан в [28]. Особенности работы машины вывода, использующей его для моделирования правдоподобных рассуждений, обсуж даются в [29]. 4.7 Проблемы и следствия Представление истинности вектором ставит ряд вопросов. Первый - содержательная интерпретация аспектов истинности. Здесь возможны как минимум два взгляда. i) аспекты истинности - это обычные нечёткие значения истинности, характеризующие объект с разных позиций. Например, истинность суждения «Автомобиль комфортен» можно характеризовать с позиций качества отделки салона, мощности двигателя, шумо-изоляции салона и т.п. Соответственно, истинность (0.3; 0.5; 0.8; ..) означает, что качество отделки салона невысоко, мощность двигателя средняя, шумоизоляция хорошая и т.д. Вектор здесь - обычный нечёткий вектор, компоненты которого принимают значения из отрезка [0, 1]. Этот взгляд достаточно очевиден (на нём основано понятие нечёткого вектора) и не заслуживает особого обсуждения. 2) аспекты - категории истинности, вроде Истины и Лжи. Значения компонентов здесь -степени выраженности соответствующей категории, определяемые поступившими свидетельствами или по иным соображениям (например, экспертно). Второй взгляд рассматриваем как основной. При этом возникает вопрос о числе и характере аспектов истинности, исчерпывающим образом описывающих реальность. Если становиться на позиции, близкие к классической логике, их всего два: Истина и Ложь. В нейтрософской логике Ф. Смарандаке три: Истина, Ложь и Нейтральность. Однако принципиальной особенностью рассматриваемого сорта логик является допущение сколь угодного количества аспектов истинности, или, что то же самое, сколь угодно большого количества компонентов вектора (a 1;.; a ). Работая, например, в рамках VTF-логики, не запрещается предполагать наличие ещё каких-либо «не учтённых» аспектов истинности (об их существовании можно даже не подозревать). Все неучтённые аспекты проецируются в точку (0; 0), не разрушая исходного формализма. В этом смысле логики с векторной семантикой действительно свободны от принципов противоречия и исключённого третьего. Любой набор аспектов истинности можно свести к полному введением «замыкания» -фиктивного компонента a+1 со значением [24]: a"+1 = 1 -a1©.©a". В этом случае a1 ©.©a" ©a"+1 > 0, что можно рассматривать как полноту вектора истинности. Однако, вопрос о том, сколько и каких аспектов истинности исчерпывающим образом описывают реальность, остаётся, хотя и переходит больше в философскую плоскость. Если их выделить, все возможные логические семантики могут быть построены на их основе. Оборотной стороной этой проблемы является построение логик и связанных с ними частных семантик на основе известных аспектов истинности. Так, нечёткая семантика получается введением двух ограничений: рассматриваются только аспекты Истина и Ложь и a+ + a- = 1, классическая - ограничениями a+, aе {0, 1} и a+ + a- = 1. В [22] упоминаются одноаспектные логики, например, с аспектом только Истина или только Ложь. Для завершенности можно ввести и 0-аспектную логику V, суждения которой вообще лишены какого-либо смысла. И так далее. Проблема полноты -вторая проблема данного типа векторных логик. Наконец третьей проблемой логик с векторной семантикой является проблема коммуникации . Если допустить наличие субъектов, мыслящих в «ортогональных логических координатах», не породит ли это проблему взаимопонимания? Так, суждения, осмысленные для нас (обычно мы мыслим в категориях Истины и Лжи) окажутся лишенными смысла для разума, мыслящего в иных категориях истинности: он спроецирует их в точку (0;.; 0). И наоборот. Данная проблема, кажется, лежит вне логики, однако тесно связана с ней. Двумя очевидными следствиями логик с векторной семантикой является расширенный взгляд на теорию множеств и теорию вероятностей. Если истинность утверждения о принадлежности объекта x множеству X считать вектором: ||x е X|| = (x 1;.; x"), - это в общем случае приводит к обобщению понятий множества, нечёткого множества, нейтрософского множества. В теории вероятности всё, так или иначе, основано на представлении о возможности благоприятных и неблагоприятных исходов некоторого опыта. Если истинность соответствующего предиката считать векторной, это расширяет понятие вероятности. Аксиоматический взгляд на вероятность ничего не меняет, т.к. векторным становится истинность утверждения о принадлежности элементарного случайного события e е Q случайному событию A cQ: ||e е A|| = (e 1;^; e”\ Учитывая место теории множеств в современной математике, можно быть уверенным, что этими примерами всё не исчерпывается. Достаточно подробное изложение рассмотренного формализма дано в [25]. Его приложение к онтологическому анализу данных и формальным онтологиям представлено в работах С.В. Смирнова и его коллег (см. напр. [30, 31]). 5 Векторизация силлогизмов Аристотеля Ещё одним направлением использования векторов в логике стала формализация силлогизмов. Это позволило не только автоматизировать их построение, но и визуализировать данный процесс [32, 33]. Хорошим примером визуализации логических конструкций служат круги Эйлера и диаграммы Эйлера-Венна (из последних работ здесь можно указать [32]). Здесь с этой целью применяют векторы, а специалисты, использующие соответствующий формализм, также говорят о нём как о векторной логике. Рисунок 4 - Логическое пространство и векторы модуса Barbara В основу формализма легло представление силлогистических рассуждений цепочками векторов в ”-мерном пространстве. Каждая посылка стандартной формы представляется как вектор, а заключение силлогизма является суммой векторов, представляющих посылки, по правилу треугольника. Векторы размещаются в т.н. логическом пространстве. Размерность пространства соответствует числу терминов, участвующих в рассуждении. Например, для категорического силлогизма (модус Barbara) это выглядит так, как показано на рисунке 4. Здесь S - субъект, M - средний термин, P -предикат. Например: Все птицы имеют крылья Все пингвины - птицы_____ Все пингвины имеют крылья На рисунке 4 S - быть пингвином, M - быть птицей, P - иметь крылья. Вектор SM, равный (-1, 1, 0) - посылка «Все пингвины - птицы», век тор MP = (0, -1, 1) - посылка «Все птицы имеют крылья», вектор SP = (-1, 0, 1) - заключение «Все пингвины имеют крылья». Заключение является суммой векторов SM и MP. Векторы, соединяющие между собой точки S, M, P, ^S, ^M, ->P, а также весь набор точек типа SM, ^SM, S^M, ^S->M, SP, S^P и им подобным с точкой O, как концом вектора, соответствуют общеутвердительным и общеотрицательным посылкам. Векторы, соединяющие точку O (начало вектора) с этими же точками - частноутвердительным и частноотрицательным. Например, вектор, соединяющий точку O с точкой SP, соответствует посылке «Некоторые S есть P». Векторы общеутвердительных посылок могут переноситься в пределах своей плоскости и называются свободными. Векторы, начинающиеся в точке O, такой воз- можностью не обладают и называются связанными. Свободные векторы перемещаются с целью формирования цепочек, подобных только что рассмотренной. Связанные векторы зафиксированы. Если можно решить задачу (осуществить заключение) посредством свободного переноса векторов и их суммирования, то результат визуализируется в виде вектора, которому может быть дана соответствующая текстовая интерпретация. Если цепочку сформировать не удаётся, силлогизм является неверным. Несмотря на известную условность, с помощью данного подхода решаются задачи моделирования некоторых предметных областей [34]. Заключение Таким образом, можно заключить, что на сегодня математический аппарат логики прошёл путь от оперирования парой чисел {0, 1} к работе с достаточно сложными векторными конструкциями. Часть из них связана с усложнением аппарата классической логики, часть -с переходом к неклассическим представлениям, часть - как средство визуализации и компьютеризации процесса рассуждений. Это не означает, что происходит вытеснение одного взгляда другими. Это говорит лишь о расширении наших возможностей в понимании и описании вещей и процессов. Новое здесь не отменяет, а дополняет известное, и векторное представление логической семантики и логических конструкций - очередной этап в этом движении.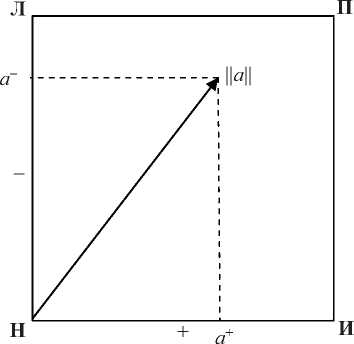
Список литературы Применение векторного формализма в логике и логико-математическом моделировании
- Пирс, Ч.С. Начала прагматизма. Том 2. Логические основания теории знаков / Пер. с англ. В.В. Кирющенко, М.В. Колопотина. - СПб.: Алетейа, 2000. - 352 с.
- Фреге, Г. Логика и логическая семантика / Г. Фреге // Перев. с нем. Б.В. Бирюкова. - М.: Аспект Пресс, 2000. - 512 с.
- Шрамко, Я.В. Истина и ложь: что такое истинностные значения и для чего они нужны / Я.В. Шрамко // Логос. - 2009. - №2(70). - С. 96-121.
- Аристотель. Сочинения. В 4-х т., т. 3 / Вступ. статья и примеч. И.Д. Рожанского.- М.: Мысль, 1981.- 613 с.
- Карпенко, А.С. Многозначные логики / А.С. Карпенко. - М.: Наука, 1997. - 223 с.


