Применение венгерского метода при решении задач распределения телекоммуникационных ресурсов для локальных сетей на подвижных платформах

Технология MHS, определяемая как локальная сеть на подвижной платформе, становится широко востребованной. Внедрение MHS позволит пассажирам высокомобильных систем, таких как скоростные поезда, морские и воздушные суда, используя свои инфокоммуникационные устройства – мобильные телефоны, ноутбуки и др., осуществлять доступ к ресурсам глобальных или корпоративных сетей. В этом случае решается проблема энергоснабжения при использовании мощных антенных систем. Наиболее перспективной является реализация MHS для железнодорожных транспортных систем [1], структурная схема которой показана на рис.1.

Согласно рис.1 общая коммуникационная сеть транспортной системы – совокупность коммутационного оборудования, которое обеспечивает передачу информационных потоков между глобальной сетью и местными информационными центрами – зональными диспетчерами (zone controllers – ZC). Сеть ZC отвечает за прием и передачу трафика, регистрацию в сети подвижной платформы и ее мобильных абонентов в зоне своей ответственности, которая представляет собой участок в несколько километров железнодорожного пути. ZC направляет информационный поток из глобальной сети одновременно на все связанные с ним ретрансляторы (repeater – R_n ), которые передают нагрузку на множество антенн (Ан ₁ ….Ан _N ), установленных на подвижной платформе. Все Ан подключены к станции подвижной платформы (vehicle station – VS), которая передает нагрузку точкам доступа (access points – АР) локальной беспроводной сети абонентов. Предлагаемая система позволяет предоставлять информационные услуги абонентам без перерывов связи [1].

Рис. 1. Структурная схема мобильного высокоскоростного доступа на примере железнодорожной транспортной системы

Модель передачи информации от зонального диспетчера к станции транспортного средства показана на рис. 2: М ретрансляторов размещены около транспортного средства и удалены друг от друга на расстояние d_r , превышающее расстояние пространственной корреляции; N антенн транспортного средства размещены на расстоянии d_a друг от друга. Самое короткое расстояние между ретранслятором и антенной подвижного объекта – d_v .

Все М × N возможных подканалов подвержены быстрым и медленным замираниям, коэффициенты подканалов остаются постоянными на длительности одного фрейма. Предполагается, что в подканалах присутствует аддитивный, белый, гауссовский шум со спектральной плотностью N₀ . Коэффициент передачи ij -го канала описывается выражением:

G^lA1, d0

где α_ij – значение огибающей, плотность распределения вероятности которой описывается распределением Райса:

cr w(tz ) = ^е

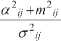
а ц т у

где

10 (—-7—) - функция Бесселя нулевого <7 "у порядка [9]; dij – расстояние между ретранслятором i и антенной j, к – образец потери тракта, L0 – уровень затухания сигнала на удалении d0 для заданного типа передающей антенны.

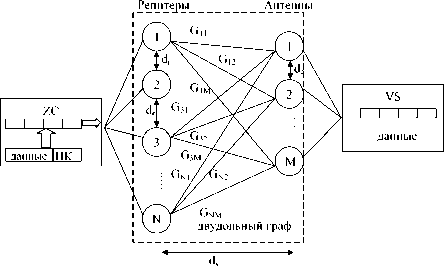
Рис. 2. Модель передачи информации от зонального диспетчера к станции транспортного средства

Поскольку d_r и d_a больше, чем расстояние пространственной корреляции подканалов, то элементы матрицы их характеристик G = ( G_ij ) взаимно независимы.

Рассматриваемая совокупность взаимосвязанных ретрансляторов и антенн может быть представлена в виде полного взвешенного двудольного графа (рис.2). Антенны и ретрансляторы представлены двумя отдельными наборами вершин. Радиолиния между каждой возможной парой антенна-ретранслятор представлена ребром графа [8]. Ребро инцидентно с вершинами различных наборов. Характеристика линии G_ij определяется как вес ребра ( i , j ). Выбор передачи с многократными радиолиниями среди всех пар антенна-ретранслятор, с ограничением непосредственной связи в каждом ретрансляторе и антенне, определяется соответствием двудольного графа: множество ребер X {(4 j)} lвсе и,й^х, может быть инцидентно на ретрансляторе i или антенне j только однажды. В матрице X — У^х уУ YХУ — ^’ если связь между i-ым ретранслятором и j-ой антенной определена на множестве Х, и x_ij = 0, если связь не выбрана. При этом сумма каждого ряда или колонки матрицы X должна быть 0 или 1 [1; 8]. Каждый i-ый ретранслятор характеризуется мощностью передаваемого сигнала Р_i и скоростью передачи r_i. Если Р_i = 0, r_i = 0, то ретранслятор неактивен. Для множества ретрансляторов определяется вектор мощности Р — [^ 31<Л/ и вектор скорости передачи информации '' = [^]1<Л/- Все образуемые беспроводные связи осуществляются на основе технологии DS/SSMA [2]. В [1] отношение мощности сигнала к мощности помехи на приеме в (ij)-ой линии определено выражением:

^ G,P, Г, N.+ ^.GgP,' (к,Г)еХ, k^i

где W – полоса пропускания системы; r_i – пропускная способность линии ( i,j ) из множества Х ; P_i – мощность сигнала ретранслятора i ; N ₀ – мощность шума в канале.

Для обеспечения требуемого качества связи необходимо, чтобы выполнялось условие:

• У, ^ Тдоп.

  
  

Тогда пропускная способность системы [1] определяется выражением:

>     _ У доп.     Х^

■system w У—* '    •             (4)

V'-j^X-Yii^Yto,,.

Постановка задачи

Из рассмотренного следует, что эффективность функционирования системы MHS определяется пропускной способностью R. Следовательно, для любых и,ПеХ,Р^Р необходимо определить ri таким образом, что Ту ^ Тдоп . Согласно выражениям (2) и (4), Rs можно представить как system

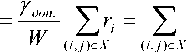
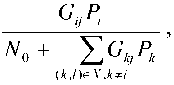
Выражение (5) является целевой функцией, а задача максимизации пропускной способности MHS представляется в виде:

Rs —> max при ограничениях:

м

^\_ц = 0 или

1; 'УХу = 0 или 1; х_у е {0,1}, (1 <  i < М, 1 < TV);

7=1 "

JV0 +

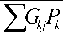
< y. * 0 <  P < P

^— / don' i ^— max *

Ограничения для x_ij в выражении (6) определены из матрицы соответствия, рассмотренной ранее.

Решение задачи (6) состоит из двух подзадач: формирования множества Х и распределения мощности передачи сигнала по ( i , j ) из Х . Первая подзадача носит комбинаторный характер, вторая – является вычислительной задачей. Одновременное решение задач вызывает большие затруднения. Поэтому предлагается, сначала получить соответствие X Kkj)}i а затем осуществить распределение мощности по числовому множеству ^iJ^Ie X.

Задача определения множества соответствия X = {(i,j)}

Задача получения множества соответствия X = {( i, j)} может быть представлена в виде целевой функции (7) и ограничений (8).

М N

ЕЕс--л ^max ’п)

z=l у=1

МN

Еу =1; Еу=1;т/ еМ,(8)

,=1

где с_ij соответствует пропускным способностям ( ij )-ых линий; Xjj G X.

Согласно ограничениям (8), решение задачи (7) может быть найдено с помощью целочисленного программирования, характеризующегося большой размерностью и временем выполнения. Однако если ввести ограничение Ху >0, то полный набор ограничений формирует ограниченную область с множеством вершин-экстремумов, которые будут соответствовать множеству Х . Следовательно, задача (7) становится задачей линейного программирования с N² переменными, которая решается быстрее [3].

Методы решения задачи

Одним из первых методов решения задачи распределения является венгерский метод Куна [4]. Сложность алгоритма оценивается O( N ³ ) числом операций. Алгоритм Hopcroft-Karp [5], который является модификацией венгерского алгоритма, позволяет решить задачу за O( N ^2.5 ) операций. Однако результаты исследований Mitra и Darby-Dowman, полученные при выполнении тестов [6], показали, что подход Hopcroft-Karp является нижней границей венгерского подхода. В [1] предлагается для учета влияния подканалов использовать их коэффициенты передачи. Тогда целевая функция может быть представлена в виде:

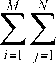
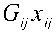
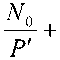
М N

Е Е^-^и к=\,к*1 /=1

М                       N

V = 1 или 0; 1 < / < Nt V х_И = 1 или 0; 1 <  i < М;

£-^ У                   J ' Z-^ У

,=|                                               ./=1

Ху е {0,1}; 1 <  j < N; 1 < / <  М.

(И)

Для учета реального воздействия на ( i , j ) линию других линий в работе [1] используется эффективный коэффициент линии

Gy = Gy---, где S^W-N –

''max keS,k*i множество активных ретрансляторов, мощность излучения которых равна :

N

I№y ^ ^max ieS 7=1

при ограничениях:

N

• 7    = 1 или 0 \ < i <      x.=\ или 0; ,

sr"         <12>

IgS; x^ e {0,1} 1 <  j gS.

Таким образом, (12) позволяет на данном множестве S получить множество соответствия Х . Определенные в Х подканалы будут характеризоваться лучшими соотношениями уровней сигналов и помех, что позволит обеспечить максимальную пропускную способность системы в целом.

Задача распределения мощности

Решение задачи распределения мощности между ретрансляторами осуществляется на основе ранее полученного множества соответствия Х . Оптимизационная функция и система ограничений могут быть представлены в виде [1]:

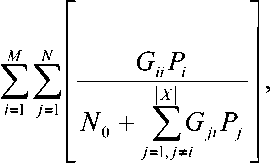
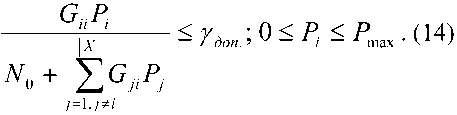
Решение задачи осуществляется c помощью симплекс-метода [3]. Для этого вводятся дополнительные переменные [1; 3], и оптимизационная задача записывается в виде:

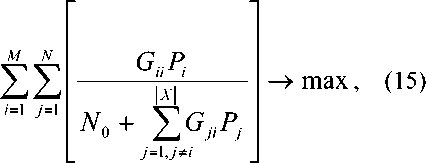
при ограничениях

G И

— P, + ILG.P, +_$, =N„;P, +t, =P„, У don.       7=1, j*i

/;,5„<>o,(i

Результаты моделирования

В работе [1] приведены результаты моделирования доступа MHS к базовой сети согласно схеме, показанной на рис.1-2, со следующими исходными данными. Пусть поезд движется со скоростью 360 км/ч = 100 м/С, для связи используется 2,4 ГГц несущая частота, есть максимальное изменение частоты Доплера f_d = 800 Гц, соответствующее время когерентности канала T_c = 0,423/∆ f_d = 530 мкС [7]; продолжительность кадра 0,1 T_c = 53 мкС. Пропускная способность системы 50 Мбит/С, 2 ^. 650 бит на фрейм. Длина поезда составляет 150 м, территориальный разнос антенны и репитеров d_r = d_a = 15 м., удаление ретрансляторов от колеи d_v = 3 м; N = 10 – число антенн на поезде; N ₀ = 1 мВт; ширина полосы пропускания системы W = 100 МГц, и γ _доп. =10 дБ. Потери на трассе k = 2,7; ближнее справочное расстояние и ослабление должны быть нормализованным к d ₀ = d _v = 3 м, L ₀ = 0 dB, соответственно, фактор Райса k = 7 дБ.

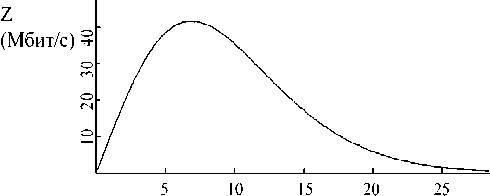
На рис.3. показаны графики значений пропускной способности системы в зависимости от скорости передачи данных в линии связи. Мобильная система, движущаяся с высокой скоростью, не может управлять элементами базовой сети. Ретрансляторы осуществляют передачу с максимально допустимой мощностью Р _max для снижения влияния внешних воздействий. Поэтому в ZC должна определяться оптимальная скорость передачи данных в образуемых линиях для обеспечения максимальной пропускной способности системы. Как видно из графика на рис.3, значение 7 Мбит/С в линии позволяет получить максимум пропускной способности системы.

г (Мбит/с)

Рис. 3. Пропускная способность системы в зависимости от скорости передачи данных в линии связи

На рис. 3 обозначены: Z – пропускная способность системы; r – скорость передачи данных в линии связи. Оптимальная системная пропускная способность зависит от взаимного расположения репитеров и антенн подвижной системы. Эта зависимость показана на рис. 4. Она достигает своего максимума, когда удаление повторителей и антенн равно d_v , и падает к ее минимуму, когда повторители и антенны являются лежащими на полпути друг между другом. Следовательно, оптимальная системная пропускная способность будет изменяться во времени, что потребует значительных затрат ресурсов управления.

Снижение колебаний возможно за счет изменения расстояний между повторителями. С увеличением расстояния амплитуды колебания значений пропускной способности системы снижаются, однако это достигается за счет снижения общей пропускной способности. На рис. 5 представлены графики зависимости пропускной способности системы от числа антенн, установленных на подвижной платформе, при заданном числе ретрансляторов.

Значения оптимальной

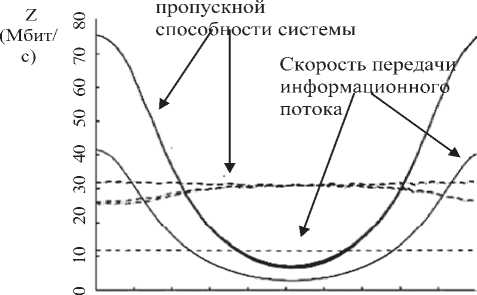
О 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Lp

Рис. 4. Значение пропускной способности системы и скорости передачи в линии связи в зависимости от взаимного удаления репитеров

На рис. 4 параметр L _p – положение репитера относительно лучшей точки связи с антенной подвижной системы

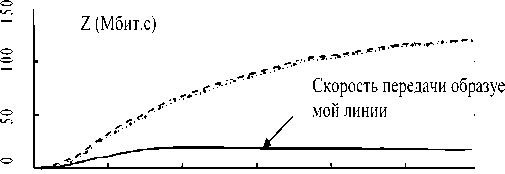
О 10      20 ^J 40     50 N

Рис.5.Зависимостьпропускнойспособностисистемы от числа антенн, установленных на подвижной платформе, при заданном числе ретрансляторов

На рис. 5 параметр N – число антенн на подвижной платформе. Анализ графиков показывает, что повышение пропускной способности системы возможно за счет увеличения числа используемых на подвижной платформе антенн до определенного значения. Это объясняется уменьшением расстояния между антеннами и усилением взаимного влияния соседних линий.

Заключение

Таким образом, проблема передвижения абонентов с высокой скоростью находит решение в виде технологии mobile hotspot. Это позволяет решить вопрос питания абонентского оборудования, использования крупногабаритных и мощных антенных систем. Снижение частоты переключения между базовыми станциями происходит из-за того, что множество ретрансляторов, подключенных к ZC, осуществляют одновременно передачу одинаковых сообщений. Исключение замираний в канале, возникающих вследствие взаимного влияния подканалов и доплеровского изменения частоты, осуществляется за счет эффективного распределения ZC мощности передачи ретрансляторами и взаимной их удаленности, определения оптимальной скорости передачи информации в образуемых линиях и количества антенн, используемых на подвижной платформе.