Применение возможностей нечетких множеств для решения задач прогнозирования и оптимизации

Решение задач оптимизации и прогнозирования результатов для последующего принятия управленческих решений на основе математического аппарата обусловлено их сложной формализацией и необходимостью построения аналитических моделей, что неизбежно приводит к затрачиванию временных и материальных ресурсов [1, 2, 3, 4]. Очень часто решение подобных задач лежит на поверхности и связано с применением субъективных представлений человека о процессах проблемной области и обработкой абстрактных сведений о решаемой задаче.

Нечеткая логика появилась в 1965 году, и была разработана профессором Лотфи Заде в Калифорнийском университете в Беркли. Состояниями нечеткой логики могут быть не только 1 или 0, но и значения между ними, то есть 0.15, 0.8 и т.д. Ее аппарат оперирует не только двумя крайними состояниями «да» и «нет», но также «конечно, да», «возможно, нет», «затрудняюсь сказать», «низкая», «высокая», «стабильный», «редкий» и т.д. Применение аппарата нечеткой логики позволило моделировать системы управления, функционирующие на основе нестрогих рассуждений на естественном человеческом языке для принятия решений в условиях неопределенности [5, 6, 7].

Предлагается рассмотреть компьютерную модель экспертной информационной системы, позволяющей прогнозировать результаты обучения по программам дополнительного профессионального обучения слушателей курсов в электронных образовательных средах.

Содержательная интерпретация нечеткой модели предполагает выбор и спецификацию входных и выходных переменных соответствующей системы нечеткого вывода. При этом в нечеткой модели предполагается использование 8 входных переменных и 1 выходную переменную.

На формирование результатов обучения, оказывает влияние множество внешних и внутренних слабо формализованных факторов, таких как дисциплина, организованность, самостоятельность, самоконтроль, посещаемость, своевременность сдачи промежуточного контроля, внимательность, активность в электроннообразовательной среде и многие другие.

В качестве основы для компьютерной модели прогнозирования результатов обучения использован аппарат нечеткой логики и механизм нечеткого вывода в среде Fuzzy Logic MATLAB.

Результатом деятельности компьютерной модели является четкое числовое прогнозное значение результатов обучения, которое может быть интерпретировано в значения: «неудовлетворительно», «удовлетворительно», «хорошо», «отлично».

B редакторе FIS определены 8 входных переменных с именами, соответствующими входам функциональной модели, и 1 выходная переменная.

При построении нечеткой модели прогнозирования успеваемости студентов было сделано предположение о том, что все рассматриваемые переменные измеряются в баллах в интервале действительных чисел от 0 до 10. При этом самая низкая оценка значения каждой из переменных является 0, а самой высокой - 10.

Для каждой входной лингвистической переменной были заданы терм-множества в диапазоне от 0 до 10, а для выходной от 0 до 100%.

В качестве терм-множества первой входной переменной «Посещаемость лекционных занятий» использовано множество Т1 = {«отличная», «хорошая», «средняя», «плохая»}.

В качестве терм-множества второй входной переменной «Посещаемость лабораторных и практических занятий» использовано аналогичное множество Т2 = {«отличная», «хорошая», «средняя», «плохая»}.

В качестве терм-множества третьей лингвистической переменной «Активность в электронной образовательной среде» задано множество Т3 = {«отличная», «хорошая», «средняя», «плохая»}.

В качестве терм-множества четвертой лингвистической переменной «Выполне- ние и защита практических работ» задано множество Т4 = {«досрочное», «своевременное», «несвоевременное»}.

В качестве терм-множества пятой лингвистической переменной «Подход к самостоятельной работе» задано множество Т5 = {«ответственный», «более-менее», «безответственный»}.

В качестве терм-множества шестой лингвистической переменной «Выполнение отчетных работ» задано множество Т6 = {«досрочное», «своевременное», «несвоевременное»}.

В качестве терм-множества седьмой лингвистической переменной «Интерес к программе ДПО» задано множество Т7 = {«высокий», «более-менее», «низкий»}.

В качестве терм-множества восьмой лингвистической переменной «Опоздания» задано множество Т8 = {«регулярные», «частые», «редкие», «не случаются»}.

В качестве терм-множества выходной лингвистической переменной «Прогнозное значение успеваемости студентов» задано множество Т9 = {«отлично», «хорошо», «удовлетворительно», «неудовлетворительно»}.

Для выходной переменной Т9 - «Прогнозное значение результатов обучения» = {Неудовлетворительно; Удовлетворительно; Хорошо; Отлично} терм-множество будет иметь диапазоны значений Неудовлетворительно = [0; 50]; Удовлетворительно = [50; 65]; Хорошо = [65; 85]; Отлично = [85; 100] (рис. 1).

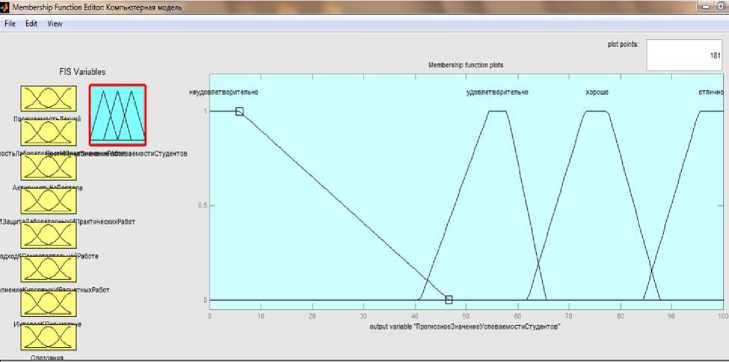
Рис. 1. Терм-множества для переменной Т9

На основе обработанных экспертных данных анкетирования педагогов сформирована база правил в количестве 100, которая введена через редактор FIS. На ос- нове которой получен нечеткий вывод по алгоритму Мамдани в виде, представленном на рисунке 2.

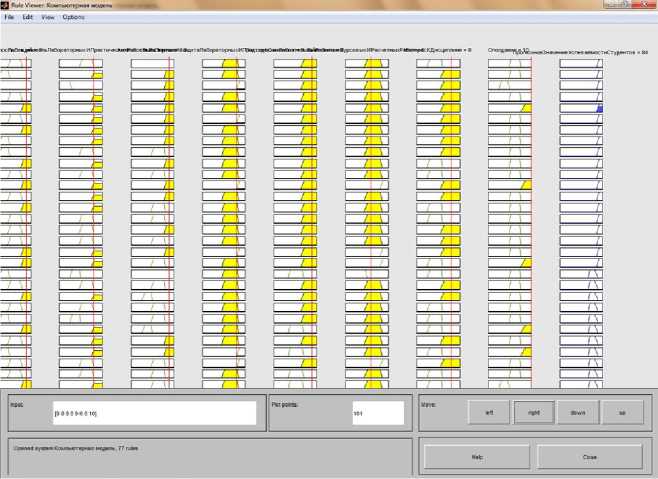
Рис. 2. Компьютерная модель нечеткой системы

Представленная модель позволяет изменять значения входных переменных в ходе учебного взаимодействия, и, с учетом базы правил лингвистических переменных, видеть прогнозное значение результатов обучения для каждого обучающего- ся, что впоследствии дает возможность применять полученный результат для корректировки образовательной территории, оптимизации учебного процесса и принятия персональных решений.

Описанный подход к моделированию может быть положен в основу для разработки нечетких информационных систем в различных сферах, в том числе и в сфере АПК, а возможными вариантами применения аппарата нечетких множеств могут быть анализ и прогнозирование урожайности сельскохозяйственных культур, молочной продуктивности крупного рогатого скота, для решения задач автоматизации технологических процессов сельского хозяйства, оценки инвестиционных рисков сельскохозяйственных объектов и проектов в АПК, энергообеспечения и электроснабжения сельскохозяйственных предприятий.