Применение высокопроизводительного вычислительного комплекса к анализу информационной динамики нейронных сетей мозга

Исследование колебательных процессов в нейронных системах мозга и выявление принципов представления и преобразования информации в мозге становятся в последние годы одними из наиболее интенсивно развивающихся направлений радиофизики. Связано это с тем, что существенно возросли возможности нейрофизиологического эксперимента, позволяющего получить все более обширную информацию о функционировании различных нейронных систем. Для исследования структур (паттернов) колебательной активности в мозге принципиальным моментом является возможность синхронного (одновременного) получения сигналов с различных нейронов сети. Методы, обеспечивающие эту возможность, обладают высоким пространственным разрешением, но вместе с тем они имеют ограничения по временному разрешению.

Новым шагом в развитии методов мониторинга коллективной активности нейронов явились многоэлектродные матрицы, способные регистрировать параллельно по нескольким электрофизиологическим каналам [1] . Эти методы позволяют не только исследовать

активность одной или нескольких отдельно взятых клеток, но и регистрировать паттерны активности сети взаимодействующих клеток, что открывает возможность экспериментально проверять гипотезы о функциональном назначении исследуемых нейросетей, изучать процессы межклеточной сигнализации, синаптической пластичности и обработки информации.

В мировой практике планарные мультиэлектродные системы применяются в основном для тестирования действия фармакологических препаратов на процессы передачи сигналов в мозге. Однако в настоящее время параллельная регистрация сигналов в культурах нейронов вызывает интерес и с точки зрения информационных приложений использования биологических модельных систем (культур) для управления нейроаниматами [2] .

Основным недостатком всех указанных экспериментальных методов является их высокая стоимость. Поэтому одним из главных направлений в данной области стала разработка математической модели нейронных культур, которая, имитируя основные функциональные возможности нейронов, использовалась бы для теоретических исследований. Подобная модель нашла бы широкое применение при радиофизическом исследовании паттернов, генерируемых культурой нейронов, а также при решении одной из узловых проблем нейрофизиологии: выявления связей информационной динамики сети с ее топологическими свойствами.

Настоящая статья предлагает метод моделирования поведения нейронных культур с учетом их важнейших свойств.

• 2.    Моделирование нейронных сетей мозга

• 3.    Простейшая задача моделирования динамики нейронной сети

С XIX века известно, что нейроны головного мозга составляют очень сложную сетевую структуру. В XX веке было широко признано, что физиологическая активность и способность обработки информации нейронных сетей зависят от их строения. Поэтому изучение строения нейронных сетей является одним из приоритетных направлений в нейрофизиологии.

Рассмотрим устройство клеток нейронов и построим математическую модель нейронных сетей.

Представим тело (сому) нейрона и его дендриты в виде круга, аксон — в виде отрезка, один конец которого совпадает с центром данного круга, а второй является свободным. Будем считать, что один нейрон соединен с другим, если свободный конец отрезка, соответствующий его аксону, находится внутри круга дендритной области второго нейрона. Таким образом, нейронную сеть можно представить в виде ориентированного графа (орграфа), вершины которого соответствуют нейронам, а ориентированное ребро, соединяющее две вершины, означает, что между соответствующими нейронами есть соединение, а также указывает направление движения сигнала.

Теория графов дает эффективный инструмент исследования нейронных сетей [3] . Известные факты и алгоритмы этой теории могут быть использованы для моделирования.

Однако использование графа в качестве модели нейронной сети не всегда оправдано и налагает ряд ограничений на архитектуру вычислительных машин. К примеру, алгоритмы графа, использующие поиск «в глубину», не могут быть эффективно реализованы на SIMD-архитектуре. Поэтому на каждой итерации матрицу смежности графа нейронной сети приходится обрабатывать, эффективно используя лишь центральный процессор, что значительно снижает скорость выполнения алгоритма.

Мы собираемся предложить метод, который столь же нагляден, как и орграф, но при этом оперирует только векторами и матрицами, тем самым предоставляя возможность использовать преимущества SIMD-архитектуры, в частности графические процессоры, а также гетерогенные grid-системы.

У каждого нейрона имеется потенциал, полученный от внешних возбудителей (потенциал действия) или возникший в силу биологических причин (потенциал покоя) [4, с. 20–51]. Если величина данного потенциала выше некоторого порогового значения, то нейрон передает сигнал всем нейронам, с которыми он соединен. После передачи сигнала нейрон вне зависимости от своего потенциала остается некоторое время неактивным. Этот отрезок времени называют периодом рефрактерности [5, с. 40–42]. Помимо этого, с течением времени у каждого нейрона потенциал уменьшается. На данном этапе будем считать, что потенциал спадает со скоростью геометрической прогрессии со знаменателем 0,9 или 0,95. Следует также отметить, что время передачи сигнала по аксону зависит от его длины: чем аксон длиннее, тем дольше идет сигнал.

Простейшая задача заключается в определении активных нейронов в каждый момент времени.

Кратко опишем алгоритм моделирования динамики нейронной сети.

Пусть задана некоторая квадратная площадка размером L х L, где L измеряется в выбранных единицах (например, нанометрах или сантиметрах). На данной площадке произвольным образом размещено N нейронов: каждому нейрону соответствуют координаты центра его дендритного круга, радиус которого равен r, и координаты свободного конца аксона. Введем обозначения:

• •    T C — вектор размера N , каждый элемент которого показывает, сколько времени (итераций) прошло после активации соответствующего нейрона;

• •    T R — вектор размера N , каждый элемент которого показывает, сколько времени соответствующий нейрон находится в периоде рефрактерности;

• •    T R — вектор размера N , каждый элемент которого показывает, сколько времени соответствующий нейрон находится в периоде рефрактерности;

• •    V — вектор размера N , элементы которого являются значениями импульсов соответствующих нейронов;

• •    N C — вектор, элементы которого показывают, от скольких соседей получил импульс нейрон.

Шаг 1. По координатам нейронов и свободных концов аксонов вычисляем матрицу смежности A соответствующего данной нейронной сети орграфа. Исключаем случай петель, то есть зануляем все элементы, стоящие на главной диагонали.

Шаг 2. Полагаем TC = (0, 0,..., 0), TR = ( го , го ,..., го ). Заполняем вектор V следующим образом: элементам с номерами соответствующих нейронов, которые активируются от внешних возбудителей, ставим значение «порогового» потенциала θ, на все остальные места — нули.

Шаг 3. Для всех i = 1, 2,..., N проверяем V i >  6 и TR i > T refract , где T _refract — период рефрактерности. Помещаем все значения i , для которых справедливы данные неравенства, в вектор I .

Шаг 4. Для всех элементов i из вектора I выполняем TR i = 0.

Шаг 5. Увеличиваем T C i на величину расстояния, пройденного сигналом по аксону за единицу времени, TR _i — на величину шага по времени для всех i ∈ I . Очищаем вектор I .

Шаг 6. Присваиваем NC = (0, 0,..., 0). Для всех нейронов проверяем A ij >  0 &  A ij 6 TC j , i, j = 1,..., N. Все значения j , для которых выполнены данные неравенства, заносим в вектор J и присваиваем TC j = 0 и NC j = NC j + 1.

Шаг 7. Переопределяем V i = 0, 9 • V i , i = 1,... N. Для всех j e J выполняем V j = V j + NC j • w, где w — значение передаваемого потенциала от нейрона к нейрону. Очищаем вектор J .

Шаг 8. Возвращаемся к шагу 3.

Выходным вектором здесь является вектор V , элементы которого содержат значения потенциалов соответствующих нейронов на каждой итерации. Активными будут те нейроны, у которых потенциал превосходит θ .

Задача моделирования нейронных сетей усложняется из-за значительного числа нейронов: десятков и сотен тысяч. Однако для каждого нейрона набор и последовательность операций одни и те же: проверить, есть ли на входе сигнал, определить по величине потенциала, активен данный нейрон или нет, передает ли его аксон сигнал или нет, а также пребывает ли нейрон в стадии периода рефрактерно-сти или нет. Поэтому проблему с многочисленностью нейронов можно разрешить, используя параллельные вычисления. Для некоторой группы нейронов запускается отдельный вычислительный поток, который проделывает все вышепредставленные операции.

Визуализировать результат можно следующим образом [6] . Отобразим множество нейронов в виде вертикальной полосы, разделенной на квадраты, каждый из которых соответствует нейрону, причём клетки активных нейронов будем закрашивать. Каждая итерация будет выдавать свою «полосу», и располагать мы их будем последовательно друг за другом по горизонтали.

На рис. 1 изображена активность первых 100 нейронов, входящих в сеть из 4000 нейронов. Произвольным образом на первой итерации

Рис. 1. Диаграмма активности первых 100 нейронов были активированы 10 нейронов. Черным цетом выделены квадраты, для которых соответствующие им нейроны на текущем шаге являются активными. На рис. 2 показано изменение числа активных нейронов по времени.

При работе использовался персональный компьютер с графическим процессором Nvidia Tesla и центральным процессором Intel Core i7.

Все арифметические и логические операции над данными были реализованы на графическом процессоре. Даже при наличии лишь одного графического ускорителя данная задача неплохо решается при общем числе нейронов порядка 5000–10000.

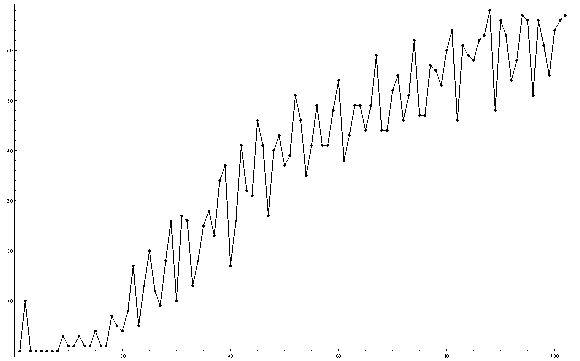
Итерация

Рис. 2. Изменение числа активных нейронов по времени

• 4.    Возможные модификации построенной модели

• 4.1.    Наличие двух типов нейронов

Построенную модель на основе опытных данных можно существенно расширить так, чтобы она описывала деятельность нейронных сетей более полно и точно. Ниже представлены некоторые возможные модификации данной модели.

Помимо нейронов, которые при возбуждении передают потенциал заданной величины другим нейронам, в действительности существуют нейроны-ингибиторы, передающие при возбуждении потенциал с противоположным знаком [7] . Данные нейроны отвечают за прерывание активности в некоторых участках нейронной сети.

Как правило, соотношение числа нейронов-ингибиторов от общего числа нейронов в сети составляет порядка 10–20%. Следует также отметить, что значение потенциала активации данных нейронов и абсолютная величина передаваемого ими потенциала больше, чем у обыкновенных нейронов, причём последний параметр у ингибиторов больше в 1,5–2 раза. Остальные характеристики тех и других нейронов одинаковы.

В соответствии с вышесказанным изменим алгоритм из предыдущего раздела. В первую очередь необходимо ввести вектор W с булевыми значениями, каждое из которых равно 1, если соответствующий нейрон относится к ингибиторам, и 0 — в противном случае. На шаге 3 условие V i >  θ заменяем V i >  θ i , где θ i определяется следующим образом:

θ i

( θ T , θ,

если W i = 1, если W i = 0;

θ T — значение «порогового» потенциала для нейронов-ингибиторов. На шаге 7 требуется сменить V j = V j + NC j • w на V j = V j + NC j • W j , где w j определяется следующим образом:

wT, wj = w,

если W j = 1 , если W j = 0;

wT — значение передаваемого потенциала нейронами-ингибиторами, причём signwt = — signw.

• 4.2.    Синаптическая пластичность нейронов

Синаптическая пластичность — это возможность изменять величину порогового потенциала нейрона. Она необходима для реализации феномена памяти и обучения. Данный механизм характерен для всех живых организмов, имеющих нервную систему. Поэтому исследование пластичности является одним из самых передовых направлений в нейрофизиологии.

Существует несколько вариантов моделирования синаптической пластичности [7, 8] , мы используем один из простейших вариантов.

Будем считать, что значение порогового импульса нейронов за время t , прошедшее с начала работы нейронной сети, определяется формулой:

• (1)                     6(t) = У — De” ^^1- " )/⁷ ,

где t ^∗ — время последнего возбуждения нейрона, θ — значение порогового импульса, 0 < D < 6, T >  0 — параметры.

Для учета синаптической пластичности в алгоритм необходимо добавить переменную t, отсчитывающую общее время работы алгоритма, и вектор TA, хранящий для каждого нейрона время его последней активации. В данном случае понадобится также отдельный вектор О пороговых потенциалов.

На шаге 2 положим О = (9,9,... ,9) t = 0, TA = (0, 0,..., 0). Условие V i >  9 шага 3 тогда изменится на V i >  O i ; здесь же присваиваем TA i = t, i е I . На шаге 4 добавляем пересчет порогового импульса в соответствии с формулой (1) :

TA i

Oi = 9 - D • exp f —T

t ,

i ∈ I.

На шаге 8 добавляем к текущему значению t единицу.

• 4.3.    Учет влияния среды на нейроны

• 4.4.    Возбуждение нейрона как случайное событие

Под воздействием внешней понимаются все воздействия на нейрон, которые возникли не за счет деятельности нейронной сети. В предыдущем разделе был показан пример действия алгоритма в результате активации на первом шаге произвольных 20 нейронов. Это воздействие можно отнести к воздействию среды. В том же примере среда была учтена только на первой итерации и в дальнейшем не рассматривалась. Однако в действительности нейрон способен самопроизвольно генерировать некоторый импульс. Влияние данного импульса в большинстве случаев незначительно.

Моделирование влияния среды на один нейрон осуществляется при помощи случайной величины с распределением Пуассона [7] . Параметр распределения Пуассона λ берется в пределах 8–10.

Добавление данной модификации в алгоритм очевидно. С помощью численных методов на каждой итерации генерируется случайная величина, распределенная по Пуассону, которая добавляется к текущему значению импульса нейрона.

Научный интерес представляет также нейронная сеть, где возбуждение нейрона является случайным процессом [8] . В этом случае считается, что активация нейрона при получении им импульса от одного соседа происходит с заранее определенной вероятностью.

Переопределим условия исходной задачи следующим образом. Известно, что нейрон при получении импульса от одного своего соседа может активироваться с вероятностью p, при этом сохраняется существование периода рефрактерности. Требуется определить активные нейроны на каждой итерации алгоритма.

Определим вначале общую вероятность возбуждения нейрона, который получил импульсы от n своих соседей.

Пусть A i , i = 1,..., n — случайное событие, возбуждение нейрона от импульса, полученного от i-го соседа. Известно, что вероятность наступления этого события равна p: P (A i ) = p. Будем считать, что данные события попарно независимы, следовательно, P (A i П A j ) = P (A i ) • P (A j ), i = j.

Обозначим через A событие активации нейрона на текущем шаге, тогда

• (2)    P (A) = 1 - (1 - P) n .

• 5.    Заключение

В исходный алгоритм для моделирования данной задачи добавим вектор NC, каждый элемент которого является числом соседей, от которых на данный нейрон пришел импульс. На шаге 2 присваиваем NC = (0, 0,..., 0).

На шаге 3 вычисляем с помощью формулы (2) вероятность активации нейрона: 1 — (1 — p) ^NC i . Случайным образом генерируется число TR i в интервале (0,1); если оно меньше вероятности T refract (TR i < T _re f _ract ), то заносим номер i нейрона в I.

На шаге 6 присваиваем NC = (0, 0,..., 0). Проверяем условие A ij >  0 &  A ij 6 TC j , i,j = 1,..., N. Для всех j, удовлетворяющих данным неравенствам, выполняем NC j = NC j + 1.

Данная статья предназначена для того, чтобы обратить внимание читателей на проблему моделирования работы нейронных сетей мозга. Описанные здесь простейшие модели лишь дают представление о направлениях исследований в нейрофизиологии и о работе настоящих нейронных сетей. Стоит заметить, что реализация этих моделей имеет теоретический интерес только в случае, когда число элементов сети (нейронов) значительно больше тысячи, что намного затрудняет процесс получения результата. Из статьи [7] известно, что для моделирования нейронной сети из 10.000 нейронов с учетом существования нейронов-ингибиторов, эффекта пластичности и воздействия среды, компьютеру Лозаннского Университета потребовалось около 8 часов на 1 миллион итераций. Поэтому для реализации моделей нейронной сети рационально использовать современные методы параллельных вычислений.

Все описанные в статье модели были реализованы на ПК. Дальнейшие исследования касаются исследования информационной динамики нейронной сети с ее топологическими свойствами. Связано это с выявлением циклов в орграфе сети и их влиянием на создание са-моподдерживающихся процессов информационной динамики. Задача поиска в графе «в глубину» не может быть эффективно распараллелена на SIMD-архитектуре, как представленные модели. Поэтому разработки в этой области должны начаться с соответствующих теоретических исследований в теории орграфов и поиска возможности распараллеливания упомянутых ранее алгоритмов.

В описанных моделях нигде не учитывалась возможность роста нейрона. С изменением физических параметров нейронов существенно может измениться вся структура сети. Теоретический интерес представляет также исследование влияния соотношения длины аксонов и дендритов на формирование автономных кластеров нейронной сети.

Существует также огромное множество других нерешенных проблем в изучении нервной системы и головного мозга. Человек только начинает делать первые шаги в изучении принципов работы своего мозга.